Numerical Estimation in Deaf and Hearing Adults

Abstract

Deaf students often lag behind hearing peers in numerical and mathematical abilities. Studies of hearing children with mathematical difficulties highlight the importance of estimation skills as the foundation for formal mathematical abilities, but research with adults is limited. Deaf and hearing college students were assessed on the Number-to-Position task as a measure of estimation, and completed standardised assessments of arithmetical and mathematical reasoning. Deaf students performed significantly more poorly on all measures, including making less accurate number-line estimates. For deaf students, there was also a strong relationship showing that those more accurate in making number-line estimates achieved higher scores on the math achievement tests. No such relationship was apparent for hearing students. Further insights into the estimation abilities of deaf individuals should be made, including tasks that require symbolic and non-symbolic estimation and which address the quality of estimation strategies being used.

1. Introduction

For reasons that remain unclear, many deaf individuals lag behind their hearing peers in numerical and mathematical skills, e.g., standardised achievement tests (Traxler, 2000), measurement and number concepts (Austin, 1975), fractions (Titus, 1995), and arithmetic (Ansell & Pagliaro, 2006; Hyde, Zevenbergen, & Power, 2003; Kelly, Lang, Mousley, & Davis, 2003). In trying to understand the simpler domain-specific precursors to mathematical learning in hearing individuals, considerable interest has been given to the role of estimation skills. Strong positive relationships have been found between acuity of symbolic and non-symbolic estimation skills and better counting, arithmetic, and magnitude comparison abilities (Booth & Seigler, 2008; LeFevre, Greenham, & Naheed, 1993), better understanding of mathematical concepts (LeFevre et al., 1993; Petitto, 1990), and better overall scores on math achievement tests (Booth & Siegler, 2006; Siegler & Booth, 2004; Halberda, Mazzocco, & Feigenson, 2008).

Estimation skills have been characterised as part of number sense. Dehaene’s ‘Number Sense Theory’, proposes that humans are born with a domain specific and biologically-rooted ability to categorise things or events in their environment according to their numerosity (Dehaene, 1997). In line with the idea of biologically rooted skills, studies of non-symbolic estimation (e.g., approximate enumeration of arrays of objects) reveal that very young infants can discriminate between different quantities, provided the ratio difference between the two arrays is sufficiently large (e.g., Xu, Spelke, & Goddard, 2005). However, researchers accept that an innate numerical competence cannot account for the rapid expansion in mathematical ability seen in school-aged children, suggesting that socially mediated numerical activities also play a role in the development of mathematical skills. Experience with numbers and counting increases the acuity and range with which individuals can make estimations of both symbolic and non-symbolic quantities and allows us to use estimation to compare a novel result/object to a known standard (e.g., in measurement), to approximate and verify answers to arithmetic problems, and to gain experience with large magnitudes that are beyond our current ability (see Sarama & Clements, 2009 for a review). We also use estimation in many everyday tasks, e.g., when considering distance, weight of objects, area, volume, time, amount of money spent, all of which require knowledge of specific measurement units.

Estimation is a translation between alternative quantitative representations; this may involve non-numerical to non-numerical translations, e.g., translating perceived loudness into line lengths, or involve numerical to numerical translations, e.g., translating a complex arithmetical problem into an estimated outcome. Other estimates involve numerical to nonnumerical translation, e.g., translating a number into a position on a number-line (the number-to-position task (NP); Siegler & Booth, 2004). The NP task is a relatively pure measure of estimation as it does not rely on knowledge of measurement units or particular entities. In this task, a line is presented with 0 at one end and 10, 100, or 1000 at the other, depending on the context. A target number is provided, and the participant is asked to estimate where its position would be located on the number-line. This task provides a clear physical measure of one’s mental representations of distances between numbers on a number-line.

Using the NP task, Siegler and Booth (2004) observed a developmental change over time from logarithmic to linear representations, a shift thought to be facilitated by greater experience and familiarity with the number range (Siegler & Opfer, 2003), which may include opportunities for incidental learning through hearing and participating in conversations about number, exposure to abstract language related to number, and generally participating in number games that may stimulate young children’s mathematical knowledge by providing a combination of spatial, temporal, kinaesthetic, and verbal/auditory cues to numerical magnitude (e.g., Anderson, 1997; Aubrey, Bottle, & Godfrey, 2003; Siegler & Ramani, 2008; Whyte & Bull, 2008).

Gregory (1998) and Kritzer (2008, 2009a) argued that because of their hearing losses and frequently impoverished language environments, some deaf children lack access to incidental learning opportunities that limit their exposure to early developing numerical concepts. As a result, they often lack the building blocks required for formal mathematics encountered later during the school years. Lacking the experiences that help to develop a precise linear representation of number, deaf children may experience delayed transition from logarithmic to linear representations and less precision in their ability to estimate number, which may have subsequent consequences for developing mathematical skills. Bull, Marschark, and Convertino (see Bull, 2008) gathered evidence from deaf and hearing college students, showing accuracy of number-line estimations to be poorer among deaf students. Based on a median split of math achievement scores that were available for a subsample of these students, both deaf and hearing students scoring below the median for their respective hearing status groups were significantly less accurate in their number-line estimations compared with those scoring above the median. These results concur with findings from hearing children that individuals who are less mathematically able have less precise representations of number. For example, Geary, Hoard, Nugent, and Byrd-Craven (2008) found that first grade children with mathematical learning difficulties were less accurate in their number-line estimates and were delayed in the development of a linear representation of number.

The current study sought to replicate this preliminary finding with a more complete sampling of number estimations on the NP task and with a measure of standardised math achievement that could be completed by both deaf and hearing adults for purposes of direct comparison. Specifically, we addressed whether deaf and hearing adults differ in their ability to estimate number positions and whether, as in studies of hearing children, individual differences in accuracy of estimates are predictive of standardised mathematical achievement.

2. Method

2.1 Participants

Thirty-nine deaf (mean age = 21.51 years, SD = 2.38, range = 17–31 years; 13 females) and 37 hearing college students (mean age = 19.76, SD = 1.60, range = 18–25 years; 18 females) participated. The groups did not differ in age, t (75) = .61, p = .11, d = .37. All were enrolled at Rochester Institute of Technology (RIT), recruited via campus advertising, and paid for their participation. RIT includes the National Technical Institute for the Deaf (NTID), but participants were recruited from across all RIT colleges. All had satisfied the same university entrance requirements. Individual testing was conducted by a senior sign language interpreter who used sign language and/or spoken language according to students’ individual preferences.

2.2 Tasks and Procedures

Number to Position task (NP)

Estimation of numerical magnitudes was assessed using a computerized number-line estimation task. On each problem, a number between 1 and 999 was presented at the top of the screen, with a horizontal number-line presented in the middle of the screen with 0 at the left end and 1000 at the right end (always presented at the same location and measuring 222mm). The experimenter explained that the participant should click on the line to show where he/she thought the number at the top should go. Participants were given one practice trial, after which the remaining numbers were presented, one at a time without feedback. The 44 numbers used on the number-line task were 3, 6, 7, 9,19, 22 52, 62, 103, 108, 158, 168, 240, 243, 289, 297, 346, 349, 387, 391, 435, 438, 470, 475, 502, 508, 586, 591, 613, 619, 690, 694, 721, 728, 760, 767, 828, 835, 874, 879, 902, 907, 962, and 970. Each number was presented twice to calculate an average positioning. Performance on the NP task correlates highly with other assessments of estimation in children, e.g., measurement and numerosity estimation (r’s between .50 and .80, Booth & Siegler, 2006). Accuracy of estimation in specific age groups has been found to be comparable across studies, despite differences in socio-economic status between samples (Booth & Siegler, 2006).

Math achievement

The Numerical Operations and Mathematical Reasoning subtests from the Wechsler Individual Achievement Test were administered (WIAT-II, Wechsler, 2005). The Numerical Operations subtest examined addition, subtraction, multiplication and division of decimal and fractional numbers, calculation of square roots, and simple and complex algebraic equations. Participants provided written answers. Reported split-half reliability for this test is .93 in this age group. For our deaf participants both internal consistency (alpha = .87) and split-half reliability (.91) for this task was high. In the Mathematical Reasoning subtest, participants were read (hearing) or signed (deaf) a set of math problems, and were also able to read along silently. Paper and pencil were provided to aid calculation and answers were spoken or signed to the examiner. Skills examined included the use of non-standard and standard measurement units, using graphs and grids, using fractions and percentages to represent quantities less than a whole, creating and solving addition, multiplication and division problems, completing patterns, solving problems related to time and money, and using probability to make predictions. Reported split-half reliability for this test is .85. For our deaf participants both internal consistency (alpha = .87) and split-half reliability (.87) for this task was high.

3. Results

Several assessments were made of participants’ numerical estimations. Firstly we examined whether estimated numerical positions were best fit by a linear or logarithmic function. For each individual participant, and subsequently for each hearing status group, curve estimation analysis was conducted whereby the absolute residuals from the linear and logarithmic regressions were compared to determine if one provided a significantly better fit to the estimations than the other. To measure the accuracy of each participant’s estimates, the percent absolute error was calculated as [(actual number estimated target number presented)/scale of number-line] × 100. For example, if a participant was asked to estimate the location of 120 on the 0 to 1000 number-line and placed his/her mark at the point corresponding to 150, the percent absolute error would be [(150-120)/1000]*100 = 3%. There was a strong correlation between the linear fit of the estimates and percent absolute error (r (74) = −.839, p < .001), and the patterns of hearing status differences and correlations with math achievement were virtually identical. For this reason, we report here the complete analyses for only one dependent measure from the NP task, the linear fit of the estimates.

All descriptive data and hearing status comparisons are shown in table 1. Age was not significantly correlated with performance on any of the tasks, so in all analyses raw scores are used, although note that analyses conducted with age standardised scores produced equivalent patterns of results. On the NP task all individual participants’ number-line estimates were best fit by a linear function. Analysis of the overall fit of the logarithmic and linear models revealed that for both deaf and hearing participants, the linear model provided a significantly better fit to the estimates of the 44 number positions compared to the logarithmic model (deaf: t (43) = 10.31, p < .001, d = 2.11; hearing: t (43) = 10.76, p < .001, d = 2.05). A comparison of the fit residuals (as a measure of fit of the linear function) revealed a lower residual (better fit) for hearing compared to deaf participants, t (43) = 3.44, p = .001, d = 0.52.

Table 1.

Mean (SD) performance on NP estimation and WIAT math achievement tests.

	Hearing	Deaf	t	d
NP % absolute error	3.72 (1.47)	4.45 (1.78)	t (75) = 1.96, p = .05	0.22
NP linear fit (R2)	.980 (.016)	.968 (.022)	t (69.58) = 2.67, p = .009	0.62
Numerical operations (max = 54)	48.00 (3.75)	43.48 (6.46)	t (61.60) = 3.74, p < .001	0.84
Math reasoning (max = 67)	62.43 (2.92)	56.46 (6.22)	t (54.57) = 5.40, p < .001	1.22

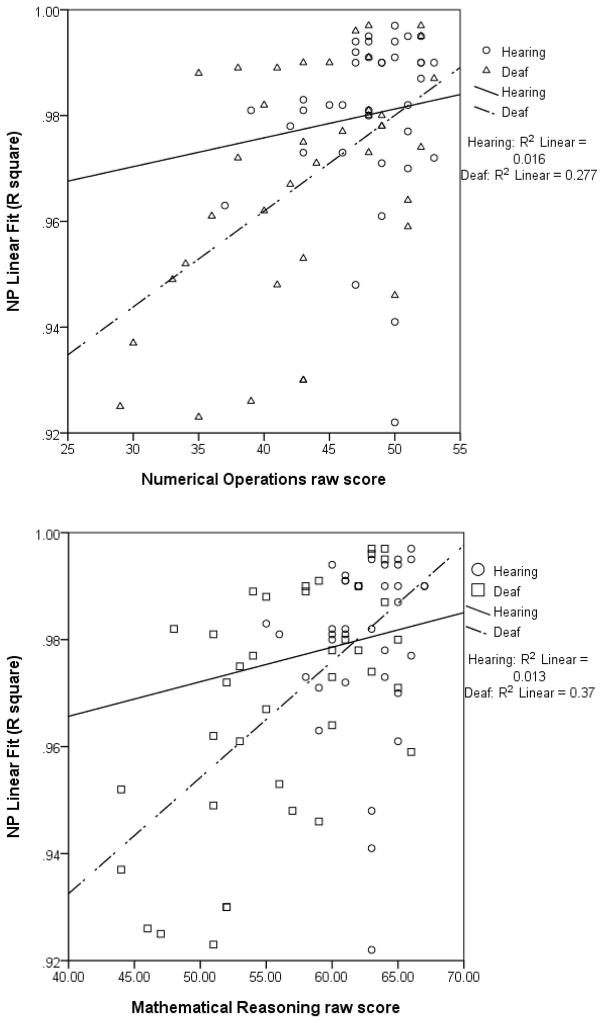
Deaf students had significantly lower scores on the Numerical Operations and Mathematics Reasoning subtests compared to hearing students. The fit of the linear function in the NP task was not found to be significantly correlated with scores on the Numerical Operations task (r (35) = .13, p = .458) or the Mathematical Reasoning task (r (35) = .12, p = .494) for hearing students. For deaf students, a better linear fit was significantly correlated with higher scores on both the Numerical Operations task (r (37) = .53, p < .001) and the Mathematical Reasoning task (r (37) = .61, p < .001, see Figure 1).

Figure 1.

Scatterplots and regression functions showing the relationship between linear fit of the numerical estimates (R²) and mathematics achievement for deaf and hearing participants (top panel = Numerical Operations; bottom panel = Mathematical Reasoning).

4. Discussion

Only a handful of studies have considered numerical estimation skills in deaf individuals and, though very exploratory in nature, this is the first study to examine whether estimation in deaf adults is a significant predictor of mathematical achievement. Whilst deaf participants showed no difference in the frequency of linear versus logarithmic best estimation fits compared to hearing individuals, the percentage absolute error between estimates and actual position on the number-line was higher, resulting in a lower fit of a linear function. Furthermore, deaf students who were less accurate in their number-line estimations scored lower on both mathematics achievement subtests. This result concurs with findings from hearing children, and our previous research, indicating that individuals who are less mathematically able have less precise representations of number as assessed through estimation tasks like that used here (Booth & Siegler, 2006; Bull, 2008; Geary et al., 2008) and using other methods to assess acuity of numerical representations (e.g., De Smedt, Vershaffel, & Ghesquiere, 2009).

Accuracy of number-line estimations did not correlate with math achievement for hearing individuals, possibly due to restricted variability in performance on the number-line estimation task and/or the presence of a non-linear relationship. Additional analyses based on a median split on each math achievement measure revealed that, contrary to our previous research (Bull, 2008), hearing individuals scoring above versus below the median in math achievement did not differ in performance on the NP estimation task. We place greater confidence in our current results which are based on a wider sampling of estimation points on the NP task. Previous studies have revealed adults with recognised numerical difficulties such as dyscalculia and acalculia to have less precise representations of number (Ashkenazi, Mark-Zigdon, & Henik, 2009; Delazer, Karner, Zamarian, Donnemiller, & Benke, 2006). Whilst none of these studies have used the NP task, less precise representations of number should be revealed by a poorer linear fit of the NP estimates, so differences in estimation on the NP task by hearing individuals may only be apparent by comparison of extreme ability groupings.

The deaf students who participated in this study are high enough achieving to attend university, reflected in their standardised scores for the mathematics tests which are normal for their age range (Numerical Operations M = 108.89, SD = 12.13; Mathematical Reasoning M = 99.41, SD = 15.82), although still significantly lower compared to their hearing peers (Numerical Operations M = 116.83, SD = 6.83; Mathematical Reasoning M = 114.67, SD = 7.48). Poorer estimation skills may be even more pronounced for those deaf children and adults who are not so high achieving. When considering the possible reasons for the poorer NP estimation of deaf adults and the relationship between NP estimation and math achievement, the most obvious predictive factor to consider is language skill. More frequent use of exact representations of number, such as Arabic numerals and counting words, may help to develop a more precise representation of number, which would then result in a better linear fit of estimations in the NP task (Siegler & Booth. 2004). Furthermore, language plays a role in transcoding the symbolic number that needs to be placed on the number-line. Therefore, language proficiency may contribute to performance on the number-line task, particularly earlier in development, and deficient language skills of deaf individuals, or fewer opportunities to engage in incidental learning opportunities that use language associated with number, may impact upon this (Gregory, 1998; Kritzer, 2009b; Marschark & Hauser, in press). Conducting an estimation task which involves non-symbolic quantities may help to determine whether poorer acuity in estimation is related to the need to transcode verbal or symbolic information, or whether poorer acuity of numerical estimation is dissociable from any language component associated with the task.

The only previous study examining numerical estimation with deaf adults used non-symbolic displays. Masataka (2006) asked deaf and hearing adults to compare two arrays (containing too many items for counting), and estimate which array contained more elements. Participants also performed an arithmetical estimation task, being asked to subtract a second array from a first array, compare this to the number of elements in a third array, and decide whether array three contained more or fewer elements compared to the subtracted array. Participants also completed a mathematics estimation task in which stimuli used for the non-symbolic subtraction task were presented as Arabic symbols. Deaf participants were as accurate as their hearing counterparts on the comparison task, and were significantly more accurate on the arithmetical approximation task. Despite their good performance on the non-symbolic tasks, deaf participants were significantly less accurate on the symbolic mathematics task. These results suggest that reduced accuracy in estimation for deaf adults may only be apparent when number meaning has to be accessed from symbols, referred to as the ‘access deficit hypothesis’ (Rouselle & Noel, 2007).

As well as the influence of language skills, one can speculate about other factors that may predict likelihood of risk for difficulties in mathematical learning, e.g., age of hearing loss, hearing status of parents, communication preferences, schooling, and educational and familial experiences. From both literature reviews (Spencer & Marschark, 2010, chapter 8) and meta-analyses of available data (Convertino, Marschark, Sapere, Sarchet, & Zupan, 2009) it appears that at present there are no consistent significant audiological, communication, or family (e.g., parental hearing status, education, and occupation) predictors of academic achievement in deaf and hard of hearing college students, above and beyond communication flexibility (integrating sign language and spoken English) and academic preparation as measured by American College Testing (ACT) scores (i.e., having the appropriate content knowledge, Convertino et al., 2009). These suggest the possibility that such variables might play a significant role in the acquisition of domain content knowledge (such as basic numeracy, estimation, etc.) earlier in development (Marschark & Hauser, in press).

Kritzer’s (2009b) finding that 60% of young deaf children demonstrated substantial delays in their understanding of mathematical concepts prior to formal schooling suggests that this may be the opportune time to consider assessment of estimation skills and, if necessary, provide early intervention with simple board games that have proved effective in improving accuracy of linear numerical estimations (e.g., Siegler & Ramani, 2008). Whilst an early delay in the acquisition of basic numerical concepts, including estimation, could account for poorer performance on the NP task of deaf college students, some may deem this unlikely given that college-aged students would have had considerable exposure to the number range and language examined in the current study. Rather it may be that deaf students are using estimation strategies of a lower quality (e.g., not using benchmarks to help with estimations) or are not giving consideration to the accuracy of their estimations. If so, this would be reflected in other mathematical tasks where we would expect to see guessing or answers that are more distant from the correct response. Although this possibility has not been addressed directly, Kelly and Mousley (2001) found that deaf college students frequently did not recognize computational errors during mathematical problem solution. Deaf college students are also significantly worse than their hearing peers in judging the accuracy of their answers on tasks following learning via both sign language and print (e.g., Borgna, Convertino, Marschark, Morrison, & Rizzolo, in press). Further consideration should be given to the estimation abilities of deaf individuals, including tasks that require symbolic and non-symbolic estimation and which address the quality of estimation strategies being used. Coupled with this, studies of deaf children are needed to establish what factors increase the risk of having difficulties in acquiring basic numerical skills, including estimation, how this impacts on academic readiness for higher level abilities, and how such difficulties can be ameliorated.