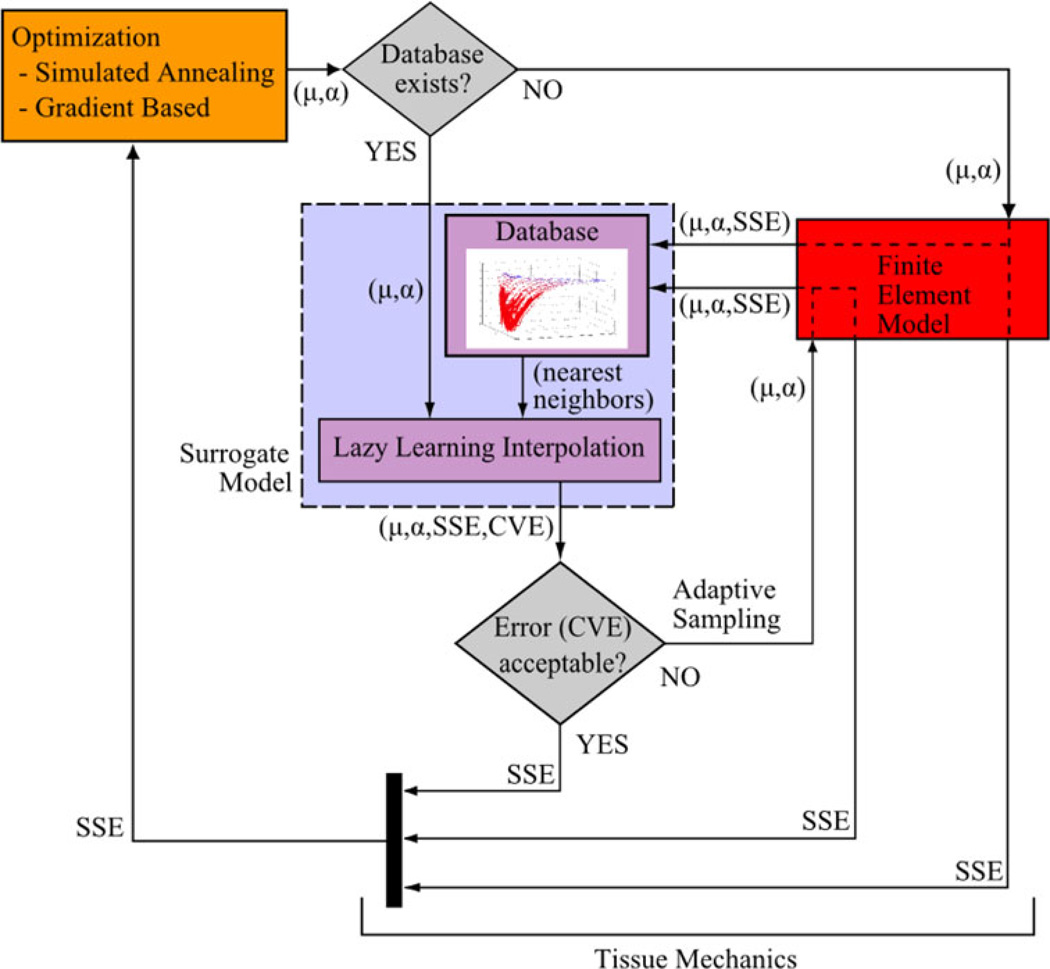
FIGURE 1.
Coupled simulation of inverse material parameter optimization focusing on the adaptive surrogate modeling approach. Material parameters are μ and α, and SSE is the corresponding model vs. experimental squared error (Eq. (2)). Note that when a finite element (FE) analysis is requested, SSE is returned back to the optimization loop and also to the surrogate model with the corresponding material parameters to expand the database. Data handling was performed in Matlab (Mathworks, Inc., Natick, MA), in which a script was developed to link the optimization with the FE through file input/output and with the surrogate representation directly. Note that the cross-validation error (CVE), as predicted by the surrogate model, was used as measure of surrogate SSE prediction accuracy. The CVE was compared with a given tolerance value (“Error (CVE) acceptable?”) to achieve the adaptive nature of the computational framework.