VOCAL FOLD MASS IS NOT A USEFUL QUANTITY FOR DESCRIBING F₀ IN VOCALIZATION

Abstract

Purpose

Confusion exists about the effect of mass and size of the vocal folds on fundamental frequency (F₀) of phonation. In particular, greater vocal fold thickness is often assumed to be associated with lower F₀. The purpose here is to show that such a relationship does not exist and that F₀ should be conceptualized with quantities other than mass, i.e., length and tissue stress.

Method

Arguments are made on the basis of fundamental laws of mechanics (point-mass versus distributed mass)

Conclusion

In speech science, phonetics, and animal vocalization disciplines, instruction should shift away from point-mass descriptions of vocal fold tissue and toward an understanding of mode frequencies in an elastic continuum.

INTRODUCTION

There is a long history in speech science and speech-language pathology of describing the fundamental frequency of vocal fold vibration (F₀) in terms of stiffness and mass of the vocal folds. The analogy with a simple oscillator, like a mass and a spring, has been so compelling and appealing that it has lived for centuries. Most introductory text books on speech science and disorders refer to this analogy (directly or indirectly) with statements like “more massive folds (longer and thicker) vibrate at naturally lower frequencies than shorter and thinner folds” (Borden et al., 1994, p. 83). In a well-used textbook on voice disorders (Colton and Casper, 1990), an inverse relation between vocal fold mass and F₀ is given (p. 289), based on measurements of vocal fold thickness (Hollien, 1962; Hollien and Colton, 1969). Although thickness is inversely related to F₀, the relation between mass and thickness is only anatomical, not functional. To be equivocal, authors often state that length, thickness, tension, and mass of the vocal folds are the key factors that influence F₀ (Ferrand, 2007, p. 54; Boone and McFarlane, 2000, p. 41), but their co-variance is often not explained.

In more recent introductory texts, the term “affective mass in vibration” is used (Hixon, Weismer and Hoit, 2008, p. 117) or the direct reference to mass is avoided in favor of stress and tissue density (Kent, 19974, p. 120; Behrman, 2007, p. 156–157). This is the correct approach, but a more detailed rationale and explanation may be useful, which is the purpose of this letter.

POINT-MASS AND DISTRIBUTED MASS SYSTEMS

In basic physics, a first exposure to mechanics is usually in the form of point-mass mechanics, for which Newton’s three laws of motion were derived. The term point-mass does not imply that an object cannot have finite dimensions, but the force-displacement relations apply to the center of mass, not to deformation of the object. If deformation occurs and this deformation is the focus of interest, Newton’s laws have to be reworked with the principles of continuum mechanics, or deformable body theory. Mass is then distributed over a region of space, and the variable that quantifies this distribution is known as density.

But what determines whether point-mass mechanics is inappropriate for a system like the vocal folds? It could be argued that the vocal folds are a small volume of tissue and a center of mass is easily identifiable. The problem is that the tissue is constrained on three of its six sides, if one thinks of the vocal fold shape as a parallelepiped. Anteriorly, posteriorly, and laterally the tissue is attached to cartilages that show relatively little vibrational movement (Titze and Strong, 1975). Hence, vibrational displacements all over the vocal fold are non-uniform, varying from maximum somewhere away from the boundary constraints to zero at the boundary constraints. Using the well-known formula for the vibrational frequency of a mass coupled to a spring

$$F_0=\frac{1}{2\pi }\sqrt{\frac{k}{m}},$$ (1)

where m is the equivalent point-mass and k is the spring stiffness, disregards the basic reality that the vocal fold is not moving anywhere (as a unit) but is deformed. Because the tissue is elastic and bounded (at the three surfaces), vibrational patterns are described in terms of modes (spatial patterns of high and low amplitude of vibration; Titze, 2006, Chapter 4). The amount of material in vibration for any one of these modes is difficult to quantify and to equate to an equivalent point-mass.

What about using the formula for a vibrating string? This formula is written as

$$F_0=\frac{1}{2L}\sqrt{\frac{\sigma }{\rho }},$$ (2)

where σ is the stress in the string, ρ is the tissue density, and L is the length. Here we have two of the variables, length and stress, that are often (correctly) credited for F₀ control. But where in this formula are thickness and depth, the inferior-superior dimension and the medial-lateral dimension, respectively? The answer is that thickness and depth are part of the stress, which is defined as tension per unit cross sectional area. In the ideal string law, however, the assumption is made that the string is thin (in cross section) compared to its length, and that all displacements are uniform across this small cross-section. This assumption does not hold for vocal folds, because the “string” is composed of several layers of tissue, none of which have the same amplitude of vibration. If each layer is considered a separate “string,” the model becomes more appropriate, as will be seen below.

F₀ AND VOCAL FOLD SIZE

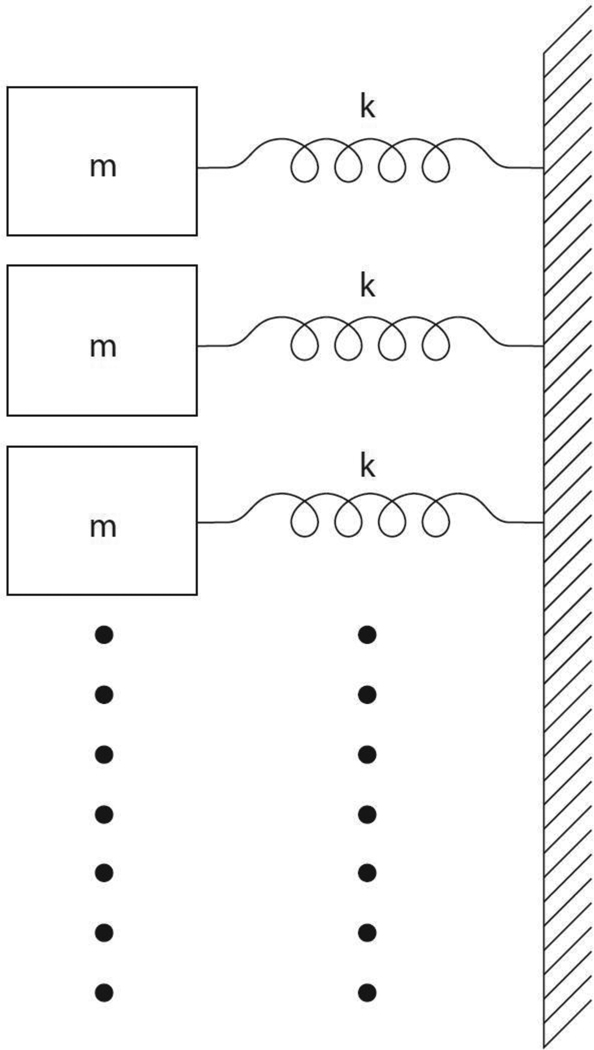
The greatest conceptual error is made with regard to vocal fold thickness. It seems intuitively correct to assume that if vocal fold thickness is doubled, mass is doubled, and hence F₀ is lowered. This is entirely erroneous, however. Consider the sketch of Figure 1, where we continue to increase vocal fold thickness by adding layers of tissue vertically. The variable m in Equation 1 now becomes the sum of all the masses m in Figure 1. With every new mass, however, there is also a new spring. The lowest natural frequency of vibration of this system of masses occurs when all masses are moving left to right in phase. For this mode, the fundamental frequency is given by Equation 1, regardless of how many masses are stacked vertically. The vocal fold could be a meter thick – there would be no change in F₀. Thus, the notion that thickness increases mass, without consideration of the added stiffness, must be abandoned. Only a localized neoplasm, like a pedunculated polyp that has no wall attachment, can be regarded as a mass-only addition.

Figure 1.

Increasing vocal fold mass vertically by changing thickness does not change F₀.

Does the same reasoning hold for a longer vocal fold? The answer here is no because of different boundary conditions. As stated above, boundary conditions determine the modes of vibration when material is deformed. For the lowest frequency mode, an approximate ½ wavelength (a half-sinusoid) pattern of vibration exists from anterior to posterior (along the length), and theoretically a ¼ wavelength (a quarter-sinusoid) pattern can exist from medial to lateral (Titze and Strong, 1975). Adding length to the vocal fold will definitely lower F₀ (all else remaining the same), but not because of mass increase. The mode frequency is lowered, which is expressed in Equation 2 by the 1/(2L) division. This decrease in F₀ will occur whether the string is thick or thin. Hence, mass is not in the length picture. As far as the medial-lateral depth is concerned, widening the vocal folds can have an effect on F₀, but recruitment of new tissue layers (e.g., more of the thryo-arytenoid muscle) will affect the effective tension much more than the overall dimension.

A FORMULA THAT HELPS GOVERN OUR THINKING

A formula for F₀, partly theoretical and partly empirical, was developed some years ago (Titze et al., 1988) and is fully described in textbook style (Titze, 2000, p. 228). For a membranous vocal fold length L_m, a passive (non-contractile) tissue stress σ_p, a tissue density ρ, a medial-lateral depth of vibration d (of which d_a is the portion belonging to the thyroarytenoid muscle), a maximum active stress σ_am and an activation level a_TA in the thyroarytenoid muscle, the formula is

$$F_0=\frac{1}{2L_m}\sqrt{\frac{{\sigma }_p}{\rho }}{\left(1+\frac{d_a}{d}\frac{{\sigma }_{am}}{{\sigma }_p}{a}_{TA}\right)}^{\frac{1}{2}}.$$ (3)

Note that the string formula (Equation 2) is embedded in this formula. In fact, it becomes the asymptote when either the TA muscle is not activated (a_TA = 0) or the vibration amplitude is small enough that no vibration reaches the muscle (d_a ≪ d). To use the formula quantitatively, the stresses (forces per unit area) of vocal fold tissues need to be known as a function of length and the depth of vibration needs to be estimated. But the formula has conceptual value without plugging in numbers. Length, stress, and muscle activation are the key variables. The quantity most related to overall mass, which is density ρ here, remains a constant, about 1.04 g/cm² for soft tissue. The effective mass in vibration is related to d_a/d, which is not a direct function of anatomical dimensions.

CONCLUSIONS

The highly tempting generalization that large vocal folds (especially thick vocal folds) produce a lower F₀ because they have more mass, needs to be abolished. Vocal fold vibration is a wave phenomenon (standing and travelling waves), in which tissue does not move uniformly and therefore no center of mass (or the mass itself) can be defined easily. Vocal fold dimensions do affect F₀, but differently for length, thickness, and depth.

For interpretation of F₀ changes due to tissue alteration (nodules, polyps, edema, dehydration, etc.), a critical question must be answered: does the added mass (fluid or solid) also add stiffness, and if so, how much? How are the mode frequencies altered in the tissues? Unless these questions can be answered, mass-loading effects of lesions and various neoplasms can also not be estimated reliably.