Mechanical control of cation channels in the myogenic response

Abstract

Microcirculatory vessel response to changes in pressure, known as the myogenic response, is a key component of a tissue's ability to regulate blood flow. Experimental studies have not clearly elucidated the mechanical signal in the vessel wall governing steady-state reduction in vessel diameter upon an increase in intraluminal pressure. In this study, a multiscale computational model is constructed from established models of vessel wall mechanics, vascular smooth muscle (VSM) force generation, and VSM Ca²⁺ handling and electrophysiology to compare the plausibility of vessel wall stress or strain as an effective mechanical signal controlling steady-state vascular contraction in the myogenic response. It is shown that, at the scale of a resistance vessel, wall stress, and not stretch (strain), is the likely physiological signal controlling the steady-state myogenic response. The model is then used to test nine candidate VSM stress-controlled channel variants by fitting two separate sets of steady-state myogenic response data. The channel variants include nonselective cation (NSC), supplementary Ca²⁺ and Na⁺, L-type Ca²⁺, and large conductance Ca²⁺-activated K⁺ channels. The nine variants are tested in turn, and model fits suggest that stress control of Ca²⁺ or Na⁺ influx through NSC, supplementary Ca²⁺ or Na⁺, or L-type Ca²⁺ channels is sufficient to produce observed steady-state diameter changes with pressure. However, simulations of steady-state VSM membrane potential, cytosolic Ca²⁺, and Na⁺ with pressure show only that Na⁺ influx through NSC channel also generates known trends with increasing pressure, indicating that stress-controlled Na⁺ influx through NSC is sufficient to generate the myogenic response.

the myogenic response has long been identified as a significant contributor to the acute regulatory response of the microvasculature (2, 21, 43), yet the governing mechanisms controlling the vascular smooth muscle (VSM) cell behavior remain unknown. Channels exhibiting stretch activation (7, 44, 51) in VSM cells have been shown to exist, which have been proposed to explain the response of microvessels to pressure. Candidate stretch-activated channels include the nonselective cation (NSC) channel that allows the influx of Na⁺, Ca²⁺, and efflux of K⁺ (7, 19), L-type Ca²⁺ channel responsible for the majority of Ca²⁺ influx initiating VSM contraction (28), and large-conductance, Ca²⁺-activated K⁺ (BK_Ca) channel, which has a large influence on the level of membrane polarization (17). Many of these studies identifying channels with mechanotransductive qualities have investigated the channels in isolation by patch clamping and exposure to exogenous substances or mechanical conditions representative of those thought to be present in the intact cellular environment. Foundational work on mechanotransductive channels focused on how the strain or tension directly affects channel-gating probabilities (39–41). It is clear that many of these channels respond to mechanical stimulation; however, it cannot be determined from these studies whether vessel wall stress or strain is the controlling mechanical stimulus and how these stimuli may control channel function in the myogenic response. Therefore, to understand how these channels are controlled and play a role in the acute regulatory response to pressure through the complex interactions in an intact single vessel, an integrated theoretical model taking into consideration VSM electrophysiology, VSM force generation, and vessel wall mechanics must be employed. Such a theoretical platform is a valuable hypothesis-testing method aimed at assessing which underlying channel function or set of functions is sufficient to describe the observed whole-vessel response and will be important in determining future experimental design.

Several detailed models of VSM electrophysiology have been previously developed and used in integrated models of acute regulation of arteriolar vessels. Yang et al. (53, 54) constructed the first detailed model of single vessel response. Their model keeps track of cytosolic Ca²⁺, K⁺, and Na⁺ incorporating L-type Ca²⁺, stretch-sensitive Na⁺/Ca²⁺/K⁺, BK_Ca, inward rectifier K⁺, delayed rectifier K⁺, and Na⁺/Ca²⁺ exchanger currents along with sarcoplasmic reticulum (SR) Ca²⁺-induced Ca²⁺ release and cytosolic buffering. Simulation protocols utilizing a depolarizing voltage pulse and applied strain were used to interrogate the model function with respect to qualitative and quantitative features from experimental studies of VSM cells. Koenigsberger et al. (24, 25) investigated the myogenic response and oscillatory behavior of microvessels known as vasomotion with a similar model but focused on the influence of stretch-activated channels that were formulated to be activated by stress in the vessel. VSM force generation based on cytosolic Ca²⁺ levels is represented in these two models using the Hai and Murphy VSM cross-bridge model (14), and both have used a vessel wall mechanics model to show the microvessel constriction and dilation. Most recently, a detailed model of Ca²⁺ dynamics in VSM cells was developed by Kapela et al. (22) and adds the nonselective cation Na⁺/Ca²⁺/K⁺ (NSC), store-operated nonselective cation Na⁺/Ca²⁺/K⁺, Ca²⁺-activated Cl⁻, Na⁺/K⁺/Cl⁻ cotransporter, plasma membrane Ca²⁺-ATPase, and Na⁺/K⁺-ATPase currents in addition to α₁-adrenoceptor activation and soluble guanylate cyclase activation with cGMP formation to account for effects of norepinephrine and nitric oxide stimulation, respectively. All channels and signaling pathways in this model are individually parameterized to fit experimental data, in most cases from VSM cells of rat mesenteric arterioles.

Even though much work has been done in these previous studies to develop computational models, applications using these models to reproduce whole-vessel experimental data have been limited. The most fundamental experiment investigating the regulatory response to pressure of single microvessels is the pressure myograph experiment (15). In this experiment a single microvessel is excised from tissue, mounted between two micropipettes, and then pressurized intraluminally with a fluid. The fluid in the vessel and the outer bath can be free of Ca²⁺, can contain a physiological concentration of Ca²⁺ and other ions, or can contain saturating levels of an agonist to represent passive, myogenically active, or maximally active vessel response, respectively. Myogenic response of these vessels under no-flow conditions has been shown to be independent of a functional endothelial layer (27, 31). Numerous such studies have been performed to characterize vessels of different sizes from different tissues and therefore provide a wealth of data to validate integrated models of vascular regulation in response to changes in pressure (3, 6, 8, 26, 34, 36, 48, 49).

A previous theoretical model describing the myogenic response was used to successfully fit passive and myogenically active pressure myograph experimental data from single isolated microvessels (4). In that study the length-tension characteristics of the active and passive components of the vessel wall were considered but subcellular details regarding channel currents and cytosolic Ca²⁺ concentrations were not explicitly treated. One significant argument made qualitatively in that and several other studies is that vessel tension or stress is likely the governing signal determining the steady state of the myogenic response (4, 18, 21). In these studies the observation was made that if vessel response was controlled by vessel wall strain the response would abolish the stimulus when steady-state vessel diameter was reduced with an increase in pressure. By combining this previous vessel wall mechanics study with detailed VSM electrophysiology and cross-bridge force generation models, we can now show compelling quantitative evidence that this is indeed the case. Additionally, different hypothetical vessel stress-controlled channels in the VSM can be tested to see which are sufficient to generate observed single vessel myogenic responses. By comparing the results we will then be able to select candidate channels that warrant detailed experimental analysis and also present the use of this model as a platform to posit and test hypotheses regarding the transduction of mechanical stimuli in the myogenic response.

METHODS

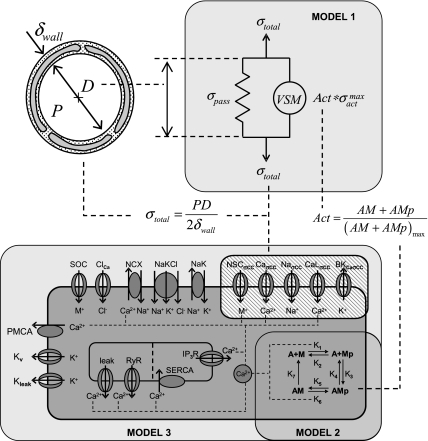
Three separate models are integrated together in this study to represent the response of a single isolated microvessel to pressure. The models and a schematic of their integration are given in Fig. 1. Model 1 decomposes the vessel wall stress into its passive and active stress components and has been parameterized to describe myogenic response data from a large number of single isolated microvessel pressure myograph experiments (4). The active stress can be related to the level of force generation as a function of cytosolic Ca²⁺ of VSM cells in the vessel wall as shown in model 2 (14, 24). Finally, the level of cytosolic Ca²⁺ in the VSM cells is determined by simulating the kinetics of Ca²⁺, Na⁺, K⁺, and Cl⁻ in the cytosol and membrane potential in model 3 (22). Additional channels or modifications of existing channels (crosshatched region in Fig. 1, model 3) have been implemented in model 3 to represent the mechanical control of vascular regulation hypotheses tested here. These nine hypothetical mechanically controlled channel variants included in this analysis are mechanical control of NSC Ca²⁺ conductance, NSC Na⁺ conductance, NSC Ca²⁺ and Na⁺ gating potential, supplementary Ca²⁺ conductance, supplementary Na⁺ conductance, L-type Ca²⁺ gating potential, L-type Ca²⁺ conductance, BK_Ca gating potential, and BK_Ca conductance.

Fig. 1.

Integrated multiscale model of myogenic response in microcirculatory vessels showing 3 submodels. Model 1: steady state vessel wall mechanics model (4). Model 2: 4-state vascular smooth muscle (VSM) cross-bridge model (14, 24). Model 3: VSM electrophysiology model (22) with vessel stress-controlled channels inserted (crosshatched). Vessel wall stress determines steady-state cytosolic Ca²⁺ levels in VSM that governs VSM activation and in turn defines the vessel diameter. See methods for details of each of these integrated models.

Model 1: vessel wall mechanics model.

The vessel wall is represented in the steady state by a nonlinear passive spring and the active stress generated by the VSM. The formulation parallels that in a previous study (4), but here the mechanics are expressed in terms of stress rather than tension. The total vessel wall stress, σ_total, is given by

$${\sigma }_{\text{total}}={\sigma }_{\text{pass}}+\text{Act}{\sigma }_{act}^{\max }$$ (1)

where σ_pass is the nonlinear passive stress, Act is the VSM activation, and σ_act^max is the maximally active stress. The total vessel wall stress is given by the Law of Laplace as

$${\sigma }_{\text{total}}=\frac{\mathrm{P}D}{2{\delta }_{\text{wall}}}$$ (2)

where P is the intraluminal pressure, D is the vessel diameter, and δ_wall is the vessel wall thickness. The thin wall cylinder approximation used here can produce significant error when estimating stress at the innermost and outermost surfaces of the vessel wall for the small resistance vessels analyzed in this study. However, we are interested in the stress experienced by the VSM cells that reside in the tunica media region of the vessel wall. If we assume the VSM cells are positioned over the middle half of the vessel wall, circumferential stresses at a given radial position predicted by the thin wall approximation are accurate to at least 15% and the average total vessel wall stress is accurate to 2%. The nonlinear passive stress is a function of diameter and is given by

$${\sigma }_{\text{pass}}=\frac{C_{\text{pass}}}{{\delta }_{\text{wall}}}\text{exp}\hspace{0.17em}\left[C_{\text{pass}}^{\prime }\left(\frac{D}{D_{\mathrm{p}100}}-1\right)\right]$$ (3)

where C_pass and C′_pass are adjustable parameters optimized to fit experimental data (4) and D_p100 is the passive diameter of the vessel at an intraluminal pressure of 100 mmHg. The maximally active stress as a function of diameter can be expressed as

$${\sigma }_{act}^{\text{max}\hspace{0.17em}}=\frac{C_{\text{act}}}{{\delta }_{\text{wall}}}\text{exp}\hspace{0.17em}\left[-{\left(\frac{D/D_{\mathrm{p}100}-C_{\text{act}}^{\prime }}{C_{act}^{″}}\right)}^2\right]$$ (4)

where C_act, C′_act, and C″_act are adjustable parameters optimized to fit experimental data (4). The cross-sectional vessel wall area, CSA_ref, is conserved in this analysis and is calculated at a reference vessel wall thickness, δ_wall,ref, and luminal diameter, D_ref, to give

$${\text{CSA}}_{\text{ref}}=\pi {\delta }_{\text{wall,ref}}\left(D_{\text{ref}}+{\delta }_{\text{wall,ref}}\right)$$ (5)

and therefore at a given diameter, D, the vessel wall thickness is given by

$${\delta }_{\text{wall}}=-\frac{D}{2}+\sqrt{{\left(\frac{D}{2}\right)}^2+\frac{{\text{CSA}}_{\text{ref}}}{\pi }}$$ (6)

In pressure myograph recordings of mesenteric and femoral small resistance arteries from Fig. 1 of Bund (3), the passive and myogenically active diameters are recorded as functions of pressure over a range of 5 to 200 mmHg. Over this range of intraluminal pressures the vessel becomes myogenically active only above 30–40 mmHg; therefore the residual stresses evident at lower pressures do not play an important role in the myogenic response. For this reason, Eqs. 1–4 are not required to accurately reproduce these stresses at low pressures. The data points at high pressure help to define the steady-state vessel diameter at full VSM activation. The average vessel wall thickness at a given reference diameter, which is critical for the formulation in terms of vessel stress used here, is given in Table 2 of Bund.

The formulation of vessel wall mechanics given by Eqs. 1–6 represents the nonmonotonic behavior of the steady-state vessel diameter as a function of pressure typically observed in pressure myograph studies. At low intraluminal pressures (0 to 30–40 mmHg), the VSM cells in the vessel wall are not activated, resulting in a purely passive dilation in vessel diameter with increasing pressure. At intermediate pressures (30–40 to 120–160 mmHg), the VSM cells become activated in the vessel wall and produce a reduction in vessel diameter with increasing pressure. At high intraluminal pressures (120–160 mmHg and greater), the VSM cells are maximally activated and again respond passively to increasing pressure. The formulation predicts hysteretic behavior at high pressure ranges depending on the magnitude, relative position, and width of the active stress components with respect to the passive stress components of the mechanics model as reflected in parameter C_act, C′_act, and C″_act and discussed in previous studies (4, 38). In the two data sets utilized here, parameterization of the vessel wall passive and active stress components predicts that the mesenteric resistance arteries do not exhibit hysteresis in their response to increasing and decreasing pressures where the femoral resistance arteries do.

The optimized values for C_pass, C′_pass, C_act, C′_act, C″_act, and D_p100 for the mesenteric and femoral small resistance arteries have been determined in a previous study (4) and are given in Supplemental Table S1 (the online version of this article contains supplemental data). The VSM activation, Act, of Eq. 1 is a function of the level of force generation by the sarcomeres of the VSM that are defined in model 2.

Model 2: VSM cross-bridge model.

Active stress in the vessel wall is generated by activation of sarcomeric contraction in the VSM cells. A four-state model of myosin binding and phosphorylation is used based on the VSM latch-state model by Hai and Murphy (14). Myosin can either be free nonphosphorylated (M), free phosphorylated (Mp), attached phosphorylated (AMp), and attached dephosphorylated (AM). The binding dynamics between states can be described by the following system of ordinary differential equations

$$\begin{array}{c}\frac{\text{dM}}{\mathrm{d}t}=-K_1\mathrm{M}+K_2\text{Mp}+K_7\text{AM}\\ \frac{\text{dMp}}{\mathrm{d}t}=K_4\text{AMp}+K_1\mathrm{M}=\left(K_2+K_3\right)\text{Mp}\\ \frac{\text{dAMp}}{\mathrm{d}t}=K_3\text{Mp}+K_6\text{AM}-\left(K_4+K_5\right)\text{AMp}\\ \frac{\text{dAM}}{\mathrm{d}t}=K_5\text{AMp}-\left(K_7+K_6\right)\text{AM}\end{array}$$ (7)

where K₁ through K₇ are the rate constants for myosin binding and phosphorylation as shown in Fig. 1. The rate constant for phosphorylation of myosin is dependent on cytosolic Ca²⁺ concentration, Ca_i, and is given by

$$K_1=K_6=\gamma {\text{Ca}}_{\mathrm{i}}^3$$ (8)

where γ is the sensitivity of cross-bridge contraction to Ca²⁺. Attached myosin in both phosphorylated and dephosphorylated states is able to generate force so the degree of activation is given by

$$\text{Act}=\frac{\text{AMp}+\text{AM}}{{\left(\text{AMp}+\text{AM}\right)}_{\max \hspace{0.17em}}}$$ (9)

where (AMp + AM)_max is the maximal concentration of myosin in attached state. All fixed parameters used in the cross-bridge model are from Koenigsberger (24) and are given in Supplemental Table S2.

Model 3: VSM electrophysiology model.

Cytosolic Ca²⁺ concentration determines cross-bridge force generation and is governed by influx of Ca²⁺ through the plasma membrane, Ca²⁺-induced Ca²⁺ release from the SR, and buffering of Ca²⁺ in the cytosol. The VSM electrophysiology model developed by Kapela et al. (22) modified by the addition of each of the nine hypothetical mechanically controlled channels proposed here is used to determine cytosolic Ca²⁺ levels and is otherwise identical in form to the published model. Initially each hypothetical channel is formulated to be controlled either by vessel wall stress or vessel wall strain to illustrate the difference between the two mechanical stimuli in terms of generating the myogenic response. After elimination of vessel wall strain as a governing stimulus, we focus on the differences between the vessel stress-controlled channel variants in replicating the myogenic response. Equations given below are for the stress-controlled formulations for each of these nine channel variants with the similarly formulated strain-controlled channel equations given in the complete set of integrated model equations contained in section 2 of the supplemental information.

The first and second channel variants are vessel stress control of Ca²⁺ or Na⁺ conductance in NSC channels, respectively, based on observations of the mechanosensitivity of NSC in VSM cells (29). In these channel variants Ca²⁺ or Na⁺ influx increases with an increase in vessel wall stress. The original formulation in Kapela et al. (22) parameterizes the channel model to murine transient receptor potential (TRP) channel data (20) specifically TRP6. The change in this formulation for the NSC with stress-controlled Ca²⁺ conductance is given by

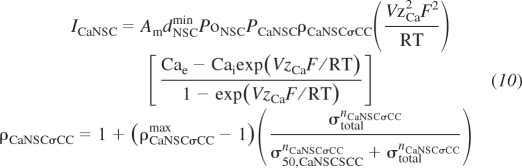(10)

where ρ_CaNSCσCC^max, σ_CaNSCσCC, and n_CaNSCσCC are the adjustable parameters defining the maximal ratio of stress-controlled to normal conductance, stress at 50% activation, and Hill exponent, respectively. I_CaNSC is the NSC Ca²⁺ current, A_m is the VSM cell surface area, d_NSC^min is the minimum constituent activation for NSC, Po_NSC is the open probability of the activation gate, P_CaNSC is the whole cell Ca²⁺ permeability for NSC, ρ_CaNSCσCC is the ratio of stress-controlled to normal conductance, V is the VSM membrane potential, z_Ca is the Ca²⁺ valence, F is Faraday's constant, R is the gas constant, T is temperature, Ca_e is the external Ca²⁺ concentration, and Ca_i is the cytosolic Ca²⁺ concentration. The formulation for the NSC with stress-controlled Na⁺ conductance is similar and given by Supplemental Eqs. S82–S83.

The third channel variant is vessel stress control of Ca²⁺ and Na⁺ NSC gating potential. This represents Ca²⁺ and Na⁺ influx at normal conductance levels at progressively more polarized membrane potentials with increasing vessel wall stress. This channel is formulated as in Kapela et al. (22) with the substitution of the following equations:

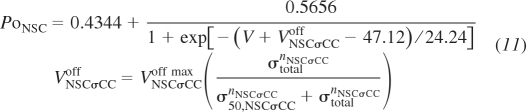(11)

where V_NSCσCC^{off max}, σ_50,NSCσCC, and n_NSCσCC are the adjustable parameters defining the maximal offset potential of the NSC activation gate, stress at 50% of the maximal offset, and the Hill exponent defining the steepness of the response, respectively, and V_NSCσCC^off is the offset potential of the activation gate.

The fourth and fifth channel variants are supplementary Ca²⁺ and Na⁺ channels, respectively, that are added to the plasma membrane to allow an additional influx of Ca²⁺ or Na⁺ as a function of vessel wall stress. These supplementary channels represent vessel stress-controlled Ca²⁺ or Na⁺ flux through channels not explicitly defined in the present model. These channels are formulated based on a standard ohmic channel representation with channel conductance controlled by vessel wall stress. The supplementary Ca²⁺ channel is inserted into the membrane to represent additional Ca²⁺ influx through a variety of possible channels including TRPM4 (45) and T-type Ca²⁺ (35, 37) channels. For the stress-controlled supplementary Ca²⁺ channel the following equations are added:

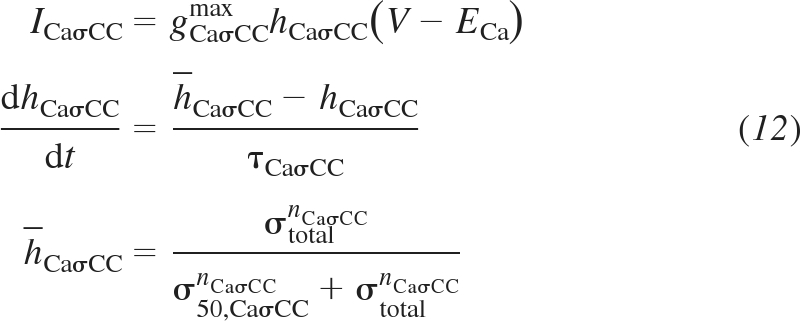(12)

where g_CaσCC^max, σ_50,CaσCC, and n_CaσCC are the adjustable parameters defining maximal channel conductance, stress at 50% activation, and Hill curve exponent, respectively. I_CaσCC is the channel current, h_CaσCC is the activation gate probability, E_Ca is the Nernst potential for Ca²⁺, h̄_CaσCC is the steady-state activation gate probability at a given vessel wall stress, and τ_CaσCC is the time constant determining the rate of change of the activation gate probability, which does not affect the steady-state solution and is arbitrarily set to 1 s to ensure stability of the integration method used. The stress-controlled supplementary Na⁺ channel is formulated in the same manner as the supplementary Ca²⁺ channel and represents an influx of Na⁺ that depolarizes the membrane potential and initiates an influx of Ca²⁺ sufficient to generate a myogenic response. This channel is added to the membrane in the same manner as with the stress-controlled supplementary Ca²⁺ channel and represents Na⁺ influx from an unspecified channel or set of channels including TRP channels (45) and voltage-gated Na⁺ (47) channels. Formulation of the stress-controlled supplementary Na⁺ channel is given by Supplemental Eqs. S25–S27.

The sixth channel variant is a modification of the L-type Ca²⁺ channel. The voltage thresholds of activation and inactivation gating probabilities are now modified to be functions of vessel stress. Therefore, instead of the formulation presented by Kapela et al. (22), the vessel stress-controlled formulation is inserted as follows:

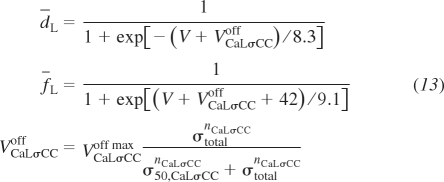(13)

where d̄_L is the steady-state activation gate probability, f̄_L is the steady-state inactivation gate probability, and V_CaσCC^off is the membrane voltage offset as a function of vessel wall stress. V_CaLσCC^{off max}, σ_50,CaLσCC, and n_CaLσCC are the maximal membrane voltage offset, 50% activation stress, and the Hill curve exponent, respectively, which are the adjustable parameters used to fit the data. This vessel stress-controlled formulation reduces to the Kapela et al. (22) model for σ_total = 0. The model could be formulated to reduce to the Kapela et al. formulation at a nonzero vessel wall stress value if suggested by experimental evidence.

The seventh channel variant is an L-type Ca²⁺ channel with stress control of the Ca²⁺ conductance. The formulation is given as

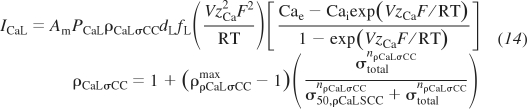(14)

where ρ_ρCaLσCC^max, σ_50,ρCaLσCC, and n_ρCaLσCC are the adjustable parameters describing the maximal stress-controlled to normal conductance ratio, the stress at 50% maximal conductance, and the Hill exponent of the activation, respectively. Other variables and parameters include I_CaL, the L-type Ca²⁺ current; P_CaL, the whole cell permeability of Ca²⁺ through L-type Ca²⁺; d_L, the L-type Ca²⁺ activation gating probability; and f_L, the L-type Ca²⁺ inactivation gating probability.

The eighth and ninth channel variants are vessel stress-controlled gating potential and conductance of the large-conductance Ca²⁺-activated K⁺ channel, respectively. This channel is known to influence membrane potential in VSM cells and therefore modulate the Ca²⁺ influx into the VSM cells through voltage-gated L-type Ca²⁺. Several groups have identified this K⁺ channel as important in the myogenic response through various mechanisms including 20-HETE inactivation (56), direct activation (23), and activation through α₅β₁ integrins (52). The description of the eighth channel variant is based on that used in Kapela et al. (22) with the following modifications resulting in depolarized mean voltage gating potentials with increasing vessel wall stress. For this formulation,

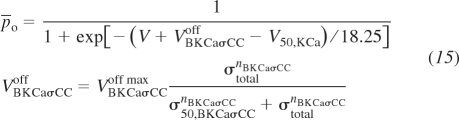(15)

where P̄_o is the steady-state fast and slow activation gate probability. V_KCaσCC^{off max}, σ_50,KCaσCC, and n_KCaσCC are the adjustable parameters as was the case with the L-type Ca²⁺ vessel stress-activated channel. In the stress-controlled BK_Ca conductance variant, an increasing vessel wall stress decreases the K⁺ efflux, eliminating the ability of BK_Ca to repolarize the VSM membrane potential. The formulation for this ninth channel variant is

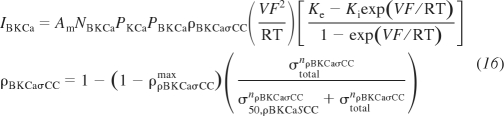(16)

where ρ_ρBKCaσCC^max, σ_{50,ρBKCaσCC}, and n_ρBKCaσCC are the adjustable parameters describing the maximal ratio of stress-controlled to normal conductance, the stress at 50% of the maximal conductance, and the Hill exponent representing the steepness of the response, respectively. Other variables and parameters are the channel density, N_BKCa; the activation gate open probability, P_KCa; the normal K⁺ permeability of the channel, P_BKCa; and the ratio of stress-controlled to normal conductance, ρ_BKCaσCC. All fixed parameters used in the VSM electrophysiology portion of the integrated model are the same as used in Kapela et al. (22) except where noted in Supplemental Table S3.

Model integration.

The three models of Fig. 1 are integrated together to represent the steady-state myogenic response to changes in intraluminal pressure. Model 1, which determines the vessel diameter as a function of VSM activation, is currently a steady-state model. Models 2 and 3, relating cytosolic Ca²⁺ to VSM activation and vessel wall stress to cytosolic Ca²⁺, respectively, are dynamic models that are numerically integrated to steady state independently before model 1 is used to calculate the vessel diameter. Model 2 is run to steady state over a range of input VSM cytosolic Ca²⁺ concentrations and then, on the basis of the steady-state VSM activation levels, a relationship between the two is parameterized. The relationship between the steady-state VSM activation and cytosolic Ca²⁺ is sigmoidal so a Hill equation is used to fit the simulation results, which is of the form

$$\text{Act}=\frac{{\text{Ca}}_{\mathrm{i}}^n}{K_{\text{M,Ca}}^n+{\text{Ca}}_{\mathrm{i}}^n}$$ (17)

where the free parameters in the optimization are n, the sensitivity of VSM activation to Ca²⁺, and K_M,Ca, the Ca²⁺ concentration at 50% VSM activation. Parameter values obtained for the VSM cross-bridge fits of VSM activation as a function of cytosolic Ca²⁺ are given in Supplemental Table S4. With this optimized fit to the simulation results, the VSM activation, Act, can be calculated from the VSM cytosolic Ca²⁺ levels generated from the VSM electrophysiology portion of the model without integrating the ordinary differential equations from model 2 for each iteration. Model 3 is also run to steady state to yield the steady-state cytosolic Ca²⁺ at a given vessel wall stress, σ_total.

Myogenic response data and optimization details.

The model is parameterized on the basis of the pressure myograph data on normal rat mesenteric and femoral small resistance arteries presented in Fig. 1 of the study by Bund (3). The data set includes passive and myogenically active steady-state responses to pressure. Since the formulation of the myogenic response proposed relates the activation of VSM contraction to total vessel stress, it is necessary to calculate vessel wall thickness at each luminal diameter according to Eq. 6. Therefore, the estimation of vessel wall cross-sectional area, CSA_ref, as given in Eq. 5, is required and the selected data sets also include vessel wall thickness, δ_wall,ref, at a reference vessel diameter, D_ref.

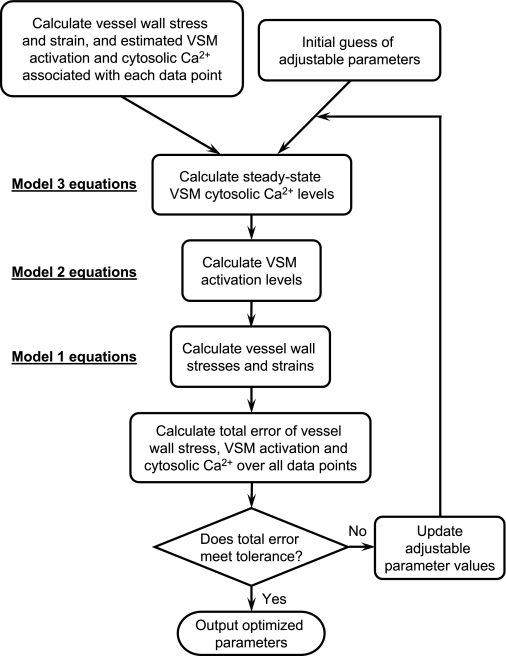
The optimizations are made to fit the model employing each of the nine mechanically controlled channel variants to the myogenically active data of the mesenteric and femoral arteriole data sets. Since at full VSM activation any cytosolic Ca²⁺ level above saturation produces a fit to the vessel diameter as a function of vessel wall stress, some adjustable parameters proved to be insensitive to optimization of the model to only the diameter-pressure data. Therefore, to yield an increased sensitivity, fits are made to three different representations of the data concurrently: vessel diameter, VSM activation, and estimated cytosolic Ca²⁺ concentration as a function of vessel wall stress. Figure 2 illustrates the optimization protocol used in this study. In each mechanically controlled channel formulation three free parameters are used to achieve the optimized fit to the data so the relative fits can be compared equivalently. The model is coded in MATLAB, the optimizations were performed by using the active-set algorithm of MATLAB's internal optimization function fmincon, and the computation was executed on a 2-GHz Intel Core Duo MacBook. A full simulation version of this model coded in MATLAB is available on our laboratory website (http://bbc.mcw.edu/Computation/models) and included in the supplemental material. Additionally the three submodels are available separately coded in Mathematical Modeling Language and implemented in the freely available JSim simulation environment (www.phyisome.org). Model names at the Physiome site are Vessel_Mechanics, VSM_4StateXB, and VSM_EphysPNaNSCSCC for models 1, 2, and 3, respectively. Detailed model versions including the optimization methods used are available from the authors upon request.

Fig. 2.

Optimization protocol for adjustable parameters to produce best fit of model to experimental data. Vessel wall stress, strain, and estimates of VSM activation and cytosolic Ca²⁺ are calculated for each data point. Initial guesses of the adjustable parameters are made to simulate the cytosolic Ca²⁺ concentration as a function of the mechanical stimulus using model 3. Model 2 and model 1 equations are then used to simulate VSM activations and vessel wall stresses and strains. The total error between calculated and simulated values is determined and if error tolerance is not met then the adjustable parameter values are updated and the simulation process is repeated.

RESULTS

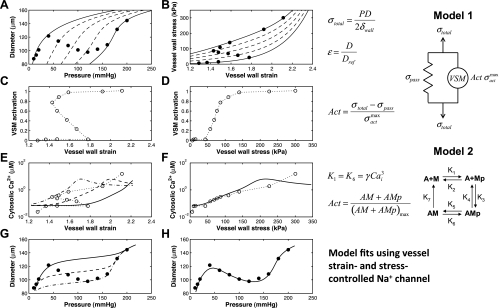
A comparison between vessel strain and vessel stress control of Na⁺ influx into VSM cells and regulation of vessel diameter in the myogenic response is investigated by using reduced versions of the fully integrated model and then by employing a strain- or stress-controlled supplementary Na⁺ channel (fifth channel variant) in the full model. The steps of this comparison are shown in Fig. 3. The experimental data of pressure vs. diameter and vessel stress vs. vessel strain from Bund (3) are shown in the top two panels (A and B) of Fig. 3. Also shown are dashed curves predicted by model 1 at different VSM activation levels. We can see that as pressure increases, increasing VSM activation is necessary to explain the myogenically active portion of the data.

Fig. 3.

Comparison between vessel strain- and vessel stress-controlled channel functions in the myogenic response. A and B: experimental data of a Wistar-Kyoto (control) rat mesenteric myogenic response from Fig. 1 of Bund (3) given in diameter-pressure (A) and stress-strain (B) domains. Strain is calculated with respect to an estimated reference passive vessel diameter at 5 mmHg. Model 1 is used to draw lines of constant VSM activation (0, 0.25, 0.5, 0.75, and 1) to show levels of activation at each data point. The 2 panels of the second row show the activation level calculated from model 1 as a function of vessel strain (C) or vessel stress (D). The third row of panels uses model 2 to estimate the cytosolic Ca²⁺ concentration at each data point, which is again plotted against vessel strain (E) and vessel stress (F). Model 2 may overestimate the cytosolic Ca²⁺ concentration at full VSM activation (last three data points here). The fully integrated model is used to show 3 different fits to Ca²⁺ as a function of vessel strain with a strain-controlled supplementary Na⁺ channel inserted into the model (E) and a single fit as a function of vessel stress with a stress-controlled supplementary Na⁺ channel (F). The bottom 2 panels show the corresponding fully integrated model fits in terms of diameter-pressure with strain-controlled (G) and stress-controlled (H) supplementary Na⁺ channels. Solid data points in this figure refer to measured experimental data whereas open data points are estimated values calculated by using model 1 and model 2 portions of the fully integrated model.

The VSM activation level necessary to match the data at each pressure value in the experimental data set is computed and plotted vs. vessel strain and vessel stress in the second row of panels (C and D) of Fig. 3. The predicted VSM activation level is not a single-valued function of vessel wall strain but rather is a monotonic function of vessel wall stress. Cytosolic Ca²⁺ levels corresponding to the predicted VSM activation levels are plotted in the third row of panels (E and F) of the figure.

Fits of the diameter vs. pressure data are shown in the bottom two panels (G and H) of Fig. 3. On the bottom left (G), the strain-controlled supplementary Na⁺ channel (Supplemental Eqs. S28–S30) is used in the VSM model. Different curves show three different parameter sets. No parameterization is able to capture the full data set using the strain-controlled supplementary Na⁺ channel. The stress-controlled supplementary Na⁺ channel (Supplemental Eqs. S25–S27) is used in the fit on the bottom right (H). This model fully captures the myogenic response using the parameters given in Table 1. The corresponding fits to estimate cytosolic Ca²⁺ levels are also shown in the third row of panels (E and F).

Table 1.

Optimized parameter values for 9 channel variants

			Value
Optimized parameter	Description	Units	Mesenteric	Femoral
NSC with stress-controlled Ca2+ conductance (CaNSCσCC)
ρCaNSCσCCmax	CaNSCσCC maximal ratio of σ-control to normal conductance	unitless	5.628	14.610
nCaNSCσCC	CaNSCσCC sensitivity to stress	unitless	3.475	1.790
σ50,CaNSCσCC	CaNSCσCC 1/2 activation stress	kPa	82.690	76.746
NSC with stress-controlled Na+ conductance (NaNSCσCC)
ρNaNSCσCCmax	NaNSCσCC maximal ratio of σ-control to normal conductance	unitless	6.997	7.931
nNaNSCσCC	NaNSCσCC sensitivity to stress	unitless	4.161	2.742
σ50,NaNSCσCC	NaNSCσCC 1/2 activation stress	kPa	82.245	34.107
NSC with stress-controlled gating voltage (NSCσCC)
VNaNSCσCCoff max	NSCsCC max offset of gating voltage	mV	403.429	665.142
nNSCσCC	NSCσCC sensitivity to stress	unitless	2.299	1.136
σ50,NSCσCC	NSCσCC 1/2 activation stress	kPa	91.222	82.789
Supp Ca2+ with stress-controlled conductance (CaσCC)
GCaσCCmax	CaσCC maximal conductance	pA/mV	2.365	3.926
nCaσCC	CaσCC sensitivity to stress	unitless	1.647	1.755
σ50,CaσCC	CaσCC 1/2 activation stress	kPa	1881.08	764.942
Supp Na+ with stress-controlled conductance (NaσCC)
gNaσCCmax	NaσCC maximal conductance	pA/mV	4.272	5.139
nNaσCC	NaσCC sensitivity to stress	unitless	2.707	1.948
σ50,NaσCC	NaσCC 1/2 activation stress	kPa	300.937	211.178
L-type Ca2+ with stress-controlled gating voltage (CaLσCC)
VCaLσCCoff max	CaLσCC maximal membrane potential offset	mV	32.490	71.636
nCaLσCC	CaLσCC sensitivity to stress	unitless	2.875	1.346
σ50,CaσCC	CaLσCC 1/2 activation stress	kPa	74.463	68.855
L-type Ca2+ with stress-controlled conductance (ρCaLσCC)
ρρCaLσCCmax	ρCaLσCC maximal ratio of σ-control to normal conductance	unitless	7.134	20.000
nρCaLσCC	ρCaLσCC sensitivity to stress	unitless	3.194	1.535
σ50,ρCaLσCC	ρCaLσCC 1/2 activation stress	kPa	76.946	84.928
BKCa with stress-controlled gating voltage (BKCaσCC)
VBKCaσCCoff max	BKCaσCC maximal membrane potential offset	mV	20.00	19.866
nBKCaσCC	BKCaσCC sensitivity to stress	unitless	2.000	2.504
σ50,BKCaσCC	BKCaσCC 1/2 activation stress	kPa	54.598	1010.50
BKCa with stress-controlled conductance (ρBKCaσCC)
ρρBKCaσCCmax	ρBKCaσCC maximal ratio of σ-control to normal conductance	unitless	0.000	0.000
nρBKCaσCC	ρBKCaσCC sensitivity to stress	unitless	2.027	1.711
σ50, ρBKCaσCC	ρBKCaσCC 1/2 activation stress	kPa	49.620	1.648

Parameter values of optimized fits of integrated model to experimental data for vessel stress-controlled nonselective cation (NSC), supplementary Ca²⁺ (Supp Ca²⁺), supplementary Na⁺ (Supp Na²⁺), L-type Ca²⁺ and large-conductance, Ca²⁺-activated K⁺ (BK_Ca) channels. Parameter values for stress-controlled voltage gating of NSC and both stress-controlled voltage gating and conductance of BK_Ca produce inadequate fits to experimental data that were found to be independent of initial guess. The fit to femoral data of the model containing an L-type Ca²⁺ channel with stress-controlled conductance produces a ρ_CaNSCσCC^max at its upper bound of the optimization range. This is an example in which transient response data is critical to uniquely define a set of parameters from the large set of virtually equivalently fitting optimized parameter values.

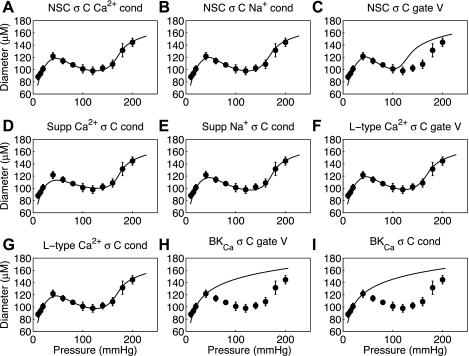
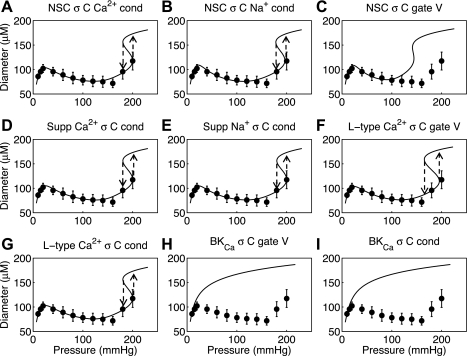
We can conclude from the analysis summarized in Fig. 3 that a Na⁺ flux tied to vessel wall strain cannot reproduce the observed myogenic response in small resistance arteries whereas a model with Na⁺ flux tied to vessel wall stress can. Fits made with strain-controlled NSC Ca²⁺, NSC Na⁺, supplementary Ca²⁺, and L-type Ca²⁺ (not shown) yield similar results to that of the strain-controlled supplementary Na⁺ channel shown in Fig. 3. Additionally, fits with stress-controlled NSC Ca²⁺, NSC Na⁺, supplementary Ca²⁺, and L-type Ca²⁺ (Fig. 4, A, B, D, F, and G) yield fits to the data equal to that shown in Fig. 3H. With stress control of Ca²⁺ or Na⁺ influx into VSM cells effective candidates for explaining the myogenic response, an investigation can be made into which individual channels activities can be controlled by vessel stress to yield the myogenic response. Fits of the fully integrated model to rat mesenteric and femoral small resistance artery myogenic responses are shown in Figs. 4 and 5, respectively. For each data set the nine different proposed vessel stress-controlled channel variants were investigated (variants of NSC, supplementary Ca²⁺, supplementary Na⁺, L-type Ca²⁺, and BK_Ca); it is seen that individually selected variants of the first four channel types produced successful fits to the data whereas the vessel stress-controlled BK_Ca was not able to reproduce a myogenic type response. The optimized parameters for each vessel stress-controlled channel are given in Table 1 in this text.

Fig. 4.

Fits to Wistar-Kyoto (control) rat mesenteric arteriole myogenic response from Bund (3) for 9 different proposed vessel stress-controlled channel variants. The 9 variants are nonselective cation (NSC) with stress-controlled (σC) Ca²⁺ conductance (cond) (A), NSC with stress-controlled Na⁺ conductance (B), NSC with stress-controlled gating voltage (gate V) (C), supplementary (Supp) Ca²⁺ with stress-controlled conductance (D), supplementary Na⁺ with stress-controlled conductance (E), L-type Ca²⁺ with stress-controlled gating voltage (F), L-type Ca²⁺ with stress-controlled conductance (G), large-conductance, Ca²⁺-activated K⁺ (BK_Ca) with stress-controlled gating voltage (H), and BK_Ca with stress-controlled conductance (I).

Fig. 5.

Fits to Wistar-Kyoto (control) rat femoral arteriole myogenic response from Bund (3) for 9 different proposed vessel stress-controlled channel variants. Panels are arranged as in Fig. 4. Hysteresis in steady-state response predicted at high pressure for increasing and decreasing pressure steps has been previously documented experimentally and described physiologically (38).

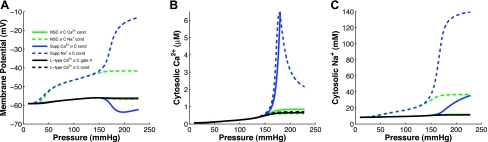
Figure 6 shows the simulated steady-state membrane potential, cytosolic Ca²⁺, and cytosolic Na⁺ for the six channel variants that successfully fit the steady-state mesenteric myogenic response data. Since the original myogenic response data did not provide concurrent membrane potential, Ca²⁺, or Na⁺ data, we are not able to definitively distinguish between these six channel variants. However, it has been well documented that membrane potential should depolarize on the order of ∼10 mV over the pressure range of 60 to 120 mmHg (16). Four of these channel variants (stress-controlled conductance of NSC Ca²⁺, supplementary Ca²⁺, and L-type Ca²⁺ and stress-controlled gating voltage of L-type Ca²⁺) show very little depolarization with increasing pressure, whereas two channel variants (stress-controlled conductance of NSC Na⁺ and supplementary Na⁺) exhibit depolarization greater than or equal to 10 mV with increasing pressure. Similarly, cytosolic Ca²⁺ and Na⁺ levels are believed to be in the 100–300 nM range and less than 40 mM, respectively; the NSC with stress-controlled Na⁺ conductance comes closest to matching these ranges.

Fig. 6.

Simulated steady-state membrane potential (A), cytosolic Ca²⁺ (B), and Na⁺ (C) with increasing intraluminal pressure for 6 of the vessel stress-controlled channel formulations that successfully fit the myogenic response data. Only the stress-controlled conductance of the NSC Na⁺ and supplementary Na⁺ show significant depolarization over the pressure range simulated. However, the cytosolic Ca²⁺ concentration with a stress-controlled supplementary Na⁺ conductance reaches levels in the μM range and cytosolic Na⁺ essentially equilibrates with extracellular Na⁺ concentrations both of which are outside of physiological levels.

DISCUSSION

The results of this study indicate that vessel stress is likely to act as the physiological signal that is effectively sensed by components of the VSM electrophysiological system. Furthermore, model-based analysis identifies which channels in the VSM cell membrane this signal could directly or indirectly be acting on. Specifically, our analysis predicts that cation channels allowing the influx of Ca²⁺ and/or Na⁺ into the VSM cell are activated in proportion to vessel wall stress. Although this study does not uncover how (direct or second-messenger pathway) the stress control is operating, it does provide an excellent theoretical platform from which further experimental investigations can be used to challenge hypotheses aimed at uncovering these subcellular mechanisms.

Vessel stress vs. strain control of cation channels in the myogenic response.

This study identifies vessel wall stress as a plausible mechanical stimulus governing the myogenic response in the microvasculature. Much of the literature on this subject invokes the concept of stretch-activated channels in the VSM involved in the myogenic response. Yet our analysis suggests the existence of a mechanism that transduces vessel wall stress to effect VSM channel activation. This mechanism still has the possibility to be more directly coupled to local stretch (strain) in the system than to vessel wall stress. Therefore, our analysis does not exclude strain-induced activation as the molecular mechanism transducing the mechanical stimulus in the myogenic response. (Indeed, stretch activation and stress control are not mutually exclusive mechanisms.) Our analysis does exclude the possibility that cation channel activities proportional to vessel wall stretch (strain) can explain the myogenic response. Whatever the molecular mechanism, sensing either local stress or strain, it apparently brings about cation channel activation in proportion to vessel wall stress. Since second messengers in the cytosol are thought to modulate the activation and inactivation of channels that facilitate an increased cytosolic Ca²⁺ and contraction, the governing stimulus could be sensed by structures other than the channels themselves. This separation between mechanisms at the channel level and the overall governing mechanical stimulus are implied in recent theoretical studies in which activation of stretch-activated channels is actually formulated to respond proportionally to vessel wall stress (5, 24, 25, 53). In all previous theoretical studies, model validation to represent the myogenic response is made only qualitatively, and comparison of different controlling mechanical stimuli and possible transduction pathways is not discussed. Second messenger involvement has been illustrated by an observed increase of 20-HETE production leading to inhibited BK_Ca and vascular constriction upon an increase in intraluminal pressure (12). Additionally, a series of studies has focused on involvement of integrins as mechanotransductive structures important to the myogenic response (32, 50, 55). In these studies it has been shown that integrins are able to transduce stimuli across the “extracellular matrix-integrin-cytoskeletal axis” and have been linked to Ca²⁺ influx through L-type Ca²⁺ channels and BK_Ca function.

Previous studies have demonstrated that vessel strain is not a governing stimulus that can explain the myogenic response known to exist experimentally (4, 21). The myogenic response following a step increase in intraluminal pressure first elicits a passive dilation of the vessel (increased vessel strain and stress) and then a constriction over time to a diameter smaller than that at the original pressure (decreased vessel strain but still an increased vessel stress). So theoretically a vessel strain-controlled channel could potentially initiate a response, but the maintenance of VSM contraction in the steady state, where the vessel strain signal would be less than at the initial pressure, must be governed by a different controlling signal than vessel wall strain. This is illustrated by the poor fits to the myogenic response diameter-pressure data of the integrated model driven by the strain-controlled supplementary Na⁺ channel shown in Fig. 3G and strain-controlled supplementary Ca²⁺, L-type Ca²⁺, and BK_Ca channels (not shown). A vessel strain-controlled vasoconstriction cannot generate the negatively sloped portion of the diameter-pressure myogenic response and could at best yield the response indicated by the solid, dashed or dash-dotted lines in Fig. 3G. These responses are myogenic in nature but not sufficient to describe the complete observed behavior of the myogenic response. At the cellular level VSM contraction is driven by the concentration of cytosolic Ca²⁺. Therefore, in the steady state, the level of cytosolic Ca²⁺ must be related to the activating signal on a one-to-one basis. Figure 3 also clearly shows that as long as VSM contraction and cytosolic Ca²⁺ are monotonically proportional, two and even three values of Ca²⁺ concentration exist for given values of vessel strain. Vessel stress on the other hand shows a one-to-one correspondence with cytosolic Ca²⁺ and accurately fits the negative sloped portion of the diameter-pressure response.

Comparison of proposed vessel stress-controlled channels.

Since several channels have been implicated in the control of VSM contraction during the myogenic response we have used this integrated model to investigate whether nine posited vessel stress-controlled variants of five different channels are able to fully describe the myogenic response experimental data. The results show that the stress-controlled conductance of NSC Ca²⁺, NSC Na⁺, supplementary Ca²⁺, supplementary Na⁺, and L-type Ca²⁺ channels and stress-controlled gating voltage of the L-type Ca²⁺ channel yield excellent fits to the steady-state diameter-pressure myogenic response data for both rat mesenteric and femoral arterioles (Figs. 4 and 5: A, B, D, E, F, and G). On the other hand, vessel stress control of either conductance or gating voltage of the BK_Ca channel and stress control of the gating voltage of NSC are not sufficient on their own to represent the myogenic response (Figs. 4 and 5: C, H, and I).

Previous experimental studies of the BK_Ca channel have identified increased channel currents when strain is applied in excised inside-out patch clamp (23) and also in whole cell patch-clamp tests (52). However, in the intact vessel myogenic response increased activation of BK_Ca upon a step increase in pressure would cause repolarization and would tend to limit or reduce the amount of vascular constriction. An additional study has implicated a mechanical control of BK_Ca through the formation of 20-HETE and the regulation of BK_Ca phosphorylation (56), which results in an inactivation of BK_Ca with increased stress or strain. That study (and our results) suggests that the BK_Ca channel can be thought of as a negative feedback mechanism in response to cytosolic Ca²⁺. If cytosolic Ca²⁺ increases through a depolarization of the membrane, the BK_Ca channel is activated eliciting an efflux of K⁺ and a repolarization of the membrane, severely inhibiting influx of Ca²⁺ across the membrane. Turning off this negative feedback mechanism through vessel stress-controlled inactivation does not in itself cause a rapid depolarization (30–90 s) of the membrane from a resting polarized state. Therefore an additional influx of Ca²⁺ or depolarization through an influx of Na⁺ is still needed for the generation of a myogenic response. Thus if the BK_Ca channel is indeed sensitive, directly or indirectly, to vessel stress, then an additional vessel stress-controlled channel producing in an influx of Ca²⁺ or Na⁺ must accompany the stress-controlled BK_Ca channel to reproduce the myogenic response.

The inability of vessel stress-controlled gating voltage of NSC to represent the myogenic response at high intraluminal pressure is consistent with experimental observations. In our simulations at pressures above 100 mmHg Na⁺ and Ca²⁺ influx induced by the stress-controlled gating voltage shift in the NSC was not able to raise the cytosolic Ca²⁺ levels enough to produce maximal VSM activation and therefore vessel diameter begins to rise at a lower pressure than observed experimentally (Figs. 4C and 5C). Experimental blockade of NSC with 10 mM DIDS (1) has been previously shown to have a significant contribution to the myogenic response by NSC; however, the pharmacological block reduces but does not eliminate the myogenic response, indicating a role of other myogenic response-generating mechanisms. Furthermore, the experiments covered an intraluminal pressure range of 20 to 100 mmHg, which does not cover the intraluminal pressure range in which NSC contribution may contribute less to the maintenance of the myogenic response. It is clear from the simulation results (Figs. 4C and 5C) that the NSC conductance of both Ca²⁺ and Na⁺ as parameterized from Kapela et al. (22) is not sufficient to be the sole generator of the myogenic response at high intraluminal pressure.

The remaining six vessel stress-controlled channel variants can be further distinguished on the basis of their simulated steady-state membrane voltage as a function of pressure. Experimental studies have shown a steady increase of membrane potential with increasing intraluminal pressure (16). Four of the six channel variants (stress-controlled conductance of NSC Ca²⁺, supplementary Ca²⁺, and L-type Ca²⁺ and stress-controlled gating voltage of L-type Ca²⁺) exhibit a relatively constant steady-state membrane potential profile with increasing pressure (Fig. 6A). This is likely due to the fact that amounts of Ca²⁺ influx sufficient to generate vasoconstriction are not sufficient to change membrane potential significantly. This leaves two channel variants (stress-controlled conductance of NSC Na⁺ and supplementary Na⁺) as channels that have the potential to describe the myogenic response data and qualitatively produce membrane depolarization with increasing pressure.

Observing the simulated cytosolic Ca²⁺ and Na⁺ in the VSM cells with increasing pressure a further distinction can be made between the two remaining viable vessel stress-controlled channel variants. Figure 6, B and C, shows that predicted cytosolic Ca²⁺ and Na⁺ achieve unrealistically high levels at high intraluminal pressures with the stress-controlled supplementary Na⁺ channel variant. Although we have no data to refute these predictions, cytosolic Ca²⁺ in the micromolar range and Na⁺ approaching equilibration with the extracellular Na⁺ concentration (140 mM) are not likely. This model response indicates that stress-controlled Na⁺ influx through NSC is sufficient to explain the generation of the myogenic response. Tracking steady-state Na⁺ concentration with respect to increased pressure by imaging with sodium-binding benzofuran isophthalate, a Na⁺ sensitive fluorescent dye (33), would challenge the hypothetical increase in Na⁺ concentration predicted in this theoretical model.

The estimated steady-state cytosolic Ca²⁺ concentrations predicted by model 2 shown in Fig. 3 strongly depends on the value specified by Koenigsberger (24) of the sensitivity of myosin phosphorylation to Ca²⁺, γ. Our model predicts cytosolic Ca²⁺ concentrations between 0.01 and 0.6 to 6 μM, which are at least one order of magnitude larger than ranges of 0.1 to 0.3 μM (57) and 0.078 to 0.129 μM (6) measured in separate experiments in rat cremaster and hamster cheek pouch arterioles, respectively. Since the study used here of the myogenic response in rat mesenteric and femoral arterioles does not report cytosolic Ca²⁺ levels, we are not able to accurately define this portion of the model. Additionally, it has been shown this sensitivity of the VSM contractile mechanics to Ca²⁺ may also vary in the myogenic response, yielding increased contraction at higher intraluminal pressure with either small or no increase in cytosolic Ca²⁺ (6). Preliminary analysis indicates that variations in force generation as a function of length, which have been incorporated into the vessel wall mechanics portion of this integrated model, are not sufficient to explain these observations. To quantify the contribution of the variable Ca²⁺ sensitivity of the contractile mechanism in the myogenic response, additional pressure myograph experiments must be performed while concurrently measuring intraluminal pressure, vessel lumen diameter, cytosolic Ca²⁺, and if possible a representative VSM membrane potential. Additionally, the pressure range must cover the full triphasic range of diameter response and a reference vessel wall thickness must be measured at a single reference vessel lumen diameter.

The experimental data currently available are sufficient to distinguish between hypothetical individual stress-controlled channel variants in the myogenic response. It is highly likely that multiple stress-controlled channels are active concurrently to determine vessel response to pressure. If multiple channel hypotheses are simulated to replicate the present data sets used here, several combinations of stress-controlled Na⁺ and Ca²⁺ influx and K⁺ efflux may successfully reproduce the data. What is evident from this study is that vessel stress-controlled inhibition of K⁺ efflux through BK_Ca and vessel stress-controlled influx of Ca²⁺ are likely not sufficient to yield membrane depolarization trends seen experimentally. Feasible combinations of multiple stress-controlled channels are suggested to include a vessel stress-controlled Na⁺ influx, which is indicated here to be through NSC channels. Further experimental investigations concurrently measuring dynamic diameter changes as a function of pressure will be required to challenge and distinguish between these multiple stress-controlled channel hypotheses.

Model as a platform for further experimental investigation.

A significant utility of this model is as a platform to propose experimental protocols targeted at uncovering the subcellular pathways responsible for transducing the vessel wall stress into regulation of cytosolic Ca²⁺ and vessel diameter. Previous studies have focused on cytochrome P-450/arachidonic acid/20-HETE as a candidate pathway important to the myogenic response (12). 20-HETE in turn has been identified as an inhibitor of BK_Ca channel opening (11). Selectively blocking the production of 20-HETE by cytochrome P-450 ω-hydroxylase (with N-methylsulfonyl-12,12-dibromododec-11-enamide) or BK_Ca (with iberiotoxin) while measuring the steady-state myogenic response and cytosolic Ca²⁺ levels will provide the necessary data to quantify the contribution of this pathway in transducing stress. Additionally, 20-HETE has been identified in the activation of L-type Ca²⁺ channel current (13). Blocking L-type Ca²⁺ with nifedipine would leave any remaining Ca²⁺ channel currents and SR Ca²⁺ release to be responsible for alteration of cytosolic Ca²⁺. This type of investigation could be done in different tissue types and on vessels at different points in the microvascular tree to assess tissue and longitudinal differences that may exist.

A recent experimental investigation has been able to measure the myogenic response while concurrently measuring VSM membrane potential by a FRET-based method and cytosolic Ca²⁺ by using fluo-4 (10). Coupling these advanced experimental methods that can concurrently provide steady-state and transient details of the intact system (diameter) and their intermediates (Ca²⁺ and membrane potential) with an integrated theoretical model for analysis has promise of elucidating the subcellular mechanisms responsible for controlling the myogenic response in the microvasculature. Other experimental methodologies such as the recently developed isovolumetric myograph (30) can also be utilized in an effort to define contractile agonist and antagonist pathway function in conjunction with this present theoretical approach.

Limitations of the model.

There are several limitations and assumptions in the developed model. The VSM electrophysiology model used in this study has largely been parameterized to represent the VSM function in rat mesenteric tissue. Mesenteric tissue in general does not experience large changes in pressure and blood flow present in other tissues such as skeletal muscle or cerebral tissue. Therefore the acute regulatory responses may be reduced in the mesentery compared with these other tissues and application of this model to data from other tissue types such as for the fourth order branch of the femoral artery used here may require further reparameterization of the ion channels describing VSM electrophysiology.

In this model the channel activation and inactivation are assumed to be a function of vessel stress and not VSM stress, which differ substantially. The VSM stress is a viable candidate signal because it monotonically increases with increasing pressure in a similar manner as vessel wall stress. Passive vessel wall stress and the difference between VSM and passive stress are not monotonically increasing with increasing pressure and therefore exhibit the same limitations as vessel wall strain does with respect to being a governing control stimulus. Assuming vessel wall stress as the controlling mechanical signal implies that the posited vessel channels are likely activated or inactivated by a mechanism that is effected by the stress or strain activation of integrins spanning the cell membrane and connecting the internal cytoskeleton of the VSM with the extracellular matrix. There is considerable experimental work indicating that this is a viable hypothesis (9). Reformulation of these vessel stress-controlled channels to be activated by VSM stress is possible if further experimental evidence indicates that VSM stress is the governing stimulus and not vessel wall stress.

This model as currently constructed is only able to represent the steady-state myogenic response; therefore we are not able to investigate the dynamic, time-dependent relationship between pressure and diameter. The VSM portions of the integrated model (models 2 and 3) are fully dynamic but are run to steady state to produce the steady-state cytosolic Ca²⁺, and then the purely steady-state vessel wall mechanics (model 1) are solved to give vessel diameter. Viscoelastic behavior of the vessel wall mechanics and kinetics of the stress transduction in VSM cells would be required to fully simulate this transient response. In addition, a more detailed treatment of Ca²⁺ handling included in the VSM electrophysiology (model 3) portion of the integrated model may be required to accurately simulate dynamic behavior.

The error associated with the thin wall approximation in average vessel wall stress across the VSM cells is expected to be less than 2% and the stress at a specific radial position in the VSM cell could vary by as much as 15%. This error is highly dependent on the assumed position of the VSM cell in the vessel wall. If the VSM position is closer to the inner surface of the vessel wall the thin wall approximation will underestimate the average vessel wall stress across the VSM. If the VSM cells actually lie closer to the external surface of the vessel wall the vessel wall stress will be overestimated by the thin wall approximation. In either case the overestimation or underestimation of average vessel wall stress represents a systematic variation from actual stress and, although it may be reflected in the optimized values of the adjustable parameters in this study, it will not affect the conclusions regarding which stress-controlled channel variants are sufficient to describe the myogenic response.

It can also be noted that optimized parameter values from this study relating to channel variants with stress-controlled controlled conductance appear to not be unique. This is because the conductance is in terms of units of time and the steady-state data cannot fully inform these parameters. However, transient response recordings as the regulatory vessels move to steady state would be sufficient to uniquely identify the magnitude of increased conductance of these vessel stress-controlled channels. The nonuniqueness of these optimized parameters to the steady-state data does not alter the conclusions made here of which vessel stress-controlled channel variants are sufficient to generate the myogenic response in resistance vessels.

Finally, recent studies showing mechanotransductive capabilities of TRP channels and their possible role in the myogenic response must be acknowledged (42, 46). The TRP6 is the only TRP channel explicitly formulated in this model. The supplementary Ca²⁺ and Na⁺ channels used in this model are generic channels used to represent the possibility of TRP and other NSC-type channels participating in the stress-controlled cytosolic Ca²⁺ levels. However, the actual response of these channels may deviate from the generic ohmic formulation utilized here. More detailed formulation of these TRP channels and other NSC-type channels based on electrophysiology observations and incorporation into this integrative model would give new insights into the relative contribution of these channels to the myogenic response.

Summary.

An integrated model describing the steady-state myogenic response of resistance vessels has been constructed incorporating VSM electrophysiology, force generation, and vessel wall mechanics. Analyzing myogenic response experimental data using this model, we have shown that the steady-state response to pressure of these vessels is physiologically governed by vessel stress and not by vessel strain. Nine vessel stress-controlled variants of five channels were tested to determine that vessel stress control of NSC Ca²⁺, NSC Na⁺, supplementary Ca²⁺, and supplementary Na⁺ or L-type Ca²⁺ channels are sufficient to generate the observed myogenic response. Vessel stress control of the BK_Ca channel resulting in channel inactivation with increased stress or vessel stress-controlled gating voltage of NSC is not sufficient on its own. Further analysis of simulated steady-state membrane potential and cytosolic Ca²⁺ and Na⁺ indicate that vessel stress-controlled Na⁺ influx through NSC is the only single vessel stress-controlled channel variant capable of fully representing the myogenic response. This integrated modeling approach can be used as a valuable test platform for the development of hypotheses and the subsequent direction of further experimental testing concerning the mechanotransductive pathways involved in the myogenic response.

GRANTS

This research was supported by National Science Foundation Grant EFRI 0735903 for B. E. Carlson and National Heart, Lung, and Blood Institute Grant HL072011 for D. A. Beard.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).