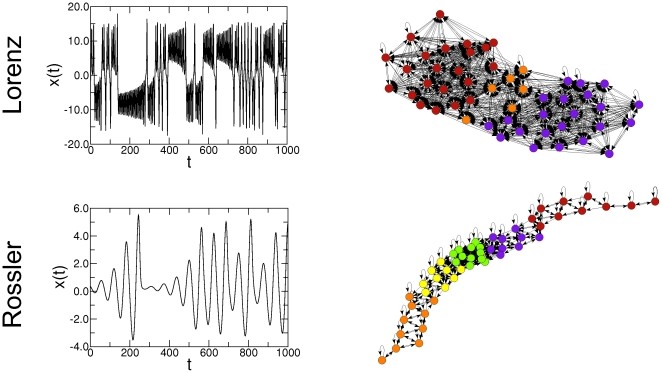
Figure 5. Illustration of the forward map 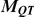 to chaotic time series from Lorenz and Rossler systems.
to chaotic time series from Lorenz and Rossler systems.
We use  10,000 time points of the
10,000 time points of the  variable of the chaotic Lorenz and Rossler equations and construct networks using
variable of the chaotic Lorenz and Rossler equations and construct networks using 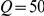 quantiles by applying the forward map. Each node is colored according to the module to which it belongs. The resulting networks display clear differences in topologies. The network of Lorenz's system is bulky with two large modules. It has a modularity value of
quantiles by applying the forward map. Each node is colored according to the module to which it belongs. The resulting networks display clear differences in topologies. The network of Lorenz's system is bulky with two large modules. It has a modularity value of 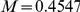 , that is much larger than the mean (standard error) modularity value
, that is much larger than the mean (standard error) modularity value 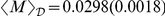 obtained from networks built from the randomizations of the original time series. Furthermore, the two lobes of the Lorenz attractor are mapped into the two largest connected modules in the network. On the other hand, the network of Rossler's system presents an elongated, chain-like pattern due the strong periodicity present in its corresponding time series. The network of Rossler's system is also modular, with five small modules and it has a modularity value of
obtained from networks built from the randomizations of the original time series. Furthermore, the two lobes of the Lorenz attractor are mapped into the two largest connected modules in the network. On the other hand, the network of Rossler's system presents an elongated, chain-like pattern due the strong periodicity present in its corresponding time series. The network of Rossler's system is also modular, with five small modules and it has a modularity value of 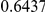 . This value is much larger than the mean (standard error) modularity value
. This value is much larger than the mean (standard error) modularity value 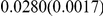 obtained from networks built from the randomizations of the original time series.
obtained from networks built from the randomizations of the original time series.