Algorithm 2.
(PET Image Recovering) Given the coefficient matrix , coincident counts , and roughness parameter μ > 0, find the intensity vector that maximizes the objective function (3.6).
| Scale E to have unit l1 column norms. |
Compute |
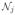 | = Σk:{j,k}∈ | = Σk:{j,k}∈
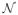 1 and aj − 2μ| 1 and aj − 2μ|
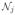 | for all 1 ≤ j ≤ p. | for all 1 ≤ j ≤ p. |
| Initialize: λ0j ← 1, j = 1, …, p. |
| repeat |
| znij ← (yieijλnj)/(Σkeikλnk) for all 1 ≤ i ≤ d, 1 ≤ j ≤ p |
| for j = 1 to p do |
bnj ← μ(|
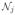 | λnj + Σk∈ | λnj + Σk∈
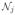 λnk) − 1 λnk) − 1 |
| cnj ← Σi znij |
| end for |
| until convergence occurs |
