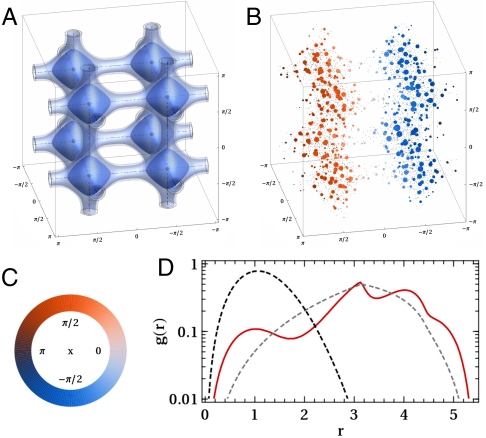
Fig. 2.

Information on a model potential (V(θ,ϕ,ψ) = exp[3(3 - sin⁴(θ) - sin⁴(ϕ) - sin⁴(ψ))] - 1), which exhibits many of the features that we believe characterize complex free-energy landscapes. In A the isosurfaces that enclose 50, 80 and 90% of the probability density for a particle diffusing about this potential at a temperature of k_BT = e³ - 1 are shown. In B the distribution of points extracted from this potential through importance sampling are shown and the 500 landmark points selected using a farthest point sampling strategy are highlighted. In this panel the size of the landmarks is related to their weights and their colors depict the value of one of the angles. A key for the coloring is shown in C, and for the remainder of this paper, wherever points are colored according to the value of an angle, we ask the reader to refer to this scale. Finally, in D we show a histogram of the distances between pairs of generated points (red). This is again compared with the distribution expected for a 3D, isotropic Gaussian (black) and the distribution for a set of points distributed uniformly across the 3D space (gray).