Figure 3.
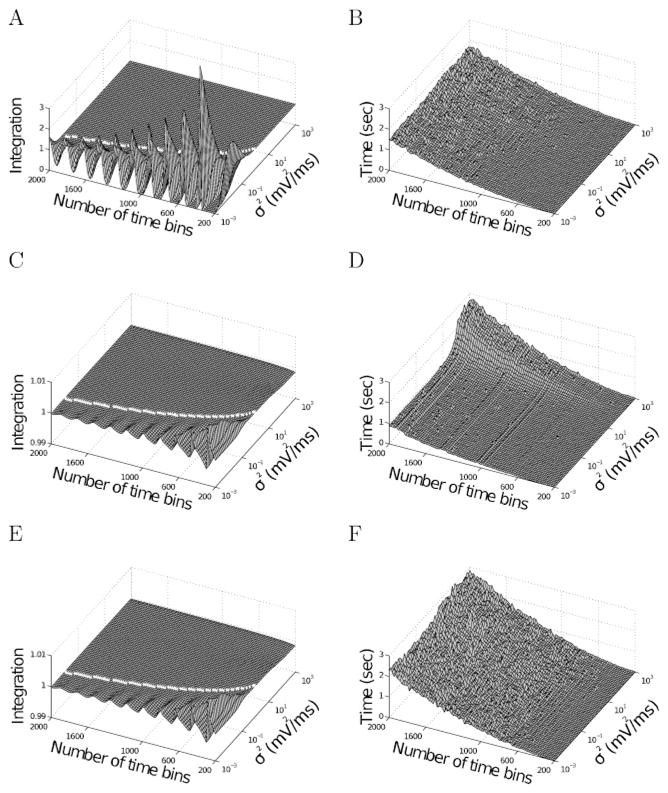
Dependence of error and computation time on noise level (σ2) and number of bins. We solved the model for a time of 20ms (as in Figure 2). (A) The integrated FPTPD using the gaussian method and (C, E) using the erf method with and without speed optimization, respectively, as a function of noise level and number of bins. Deviations from unity represent numerical error (note the different axes). The white line shows the approximate limit where the instabilities start; it is computed in equation 3.4. (B) Shows the computation (wall-clock) time using one processor (AMD Phenom II X4 955 using Matlab 7.0) for the gaussian method. (D, F) Shows the erf method without and with speed optimization, respectively. For large noise levels, the computation time increases since the speed optimization algorithm from section 4 loses efficacy because the probability is spread over several bins.
