Neural Networks Associated with the Speed-Accuracy Tradeoff: Evidence from the Response Signal Method

Abstract

This functional neuroimaging (fMRI) study examined the neural networks (spatial patterns of covarying neural activity) associated with the speed-accuracy tradeoff (SAT) in younger adults. The response signal method was used to systematically increase probe duration (125, 250, 500, 1,000 2,000 ms) in a nonverbal delayed-item recognition task. A covariance-based multivariate approach identified three networks that varied with probe duration – indicating that the SAT is driven by three distributed neural networks.

The ability to weigh the consequences of responding quickly against the consequences of responding accurately is an important component of both animal and human decision-making [1, 2]. The speed-accuracy tradeoff (SAT) refers to the common observation that accuracy decreases when the pressure to respond quickly is emphasized, while response time increases when the pressure to respond accurately is emphasized [3]. In other words, an increase in accuracy is associated with an increase in response time, and vice versa. Contemporary decision-making models assume that following stimulus presentation, baseline neural activity increases until it reaches a decision threshold and, consequently, the SAT depends upon the distance between baseline neural activity and the decision threshold, and the rate at which information regarding the decision accumulates [1, 4, 5]. Although the SAT is central to many contemporary models of decision making, the neural mechanisms associated with the SAT remain poorly understood. To date, only three functional neuroimaging (fMRI) studies have examined the neural mechanisms associated with the SAT [6–8]. These studies indicated that neural activity in the pre-supplementary motor area (pre-SMA; BA 6) and striatum, rather than in the sensory or primary motor cortices increased when individuals were instructed to emphasize speed compared to when individuals were instructed to emphasize accuracy. These three studies also suggested that the increased neural activity observed in the pre-SMA and striatum during speed emphasis reflected an increase in baseline neural activity rather than a decrease in (or a lowering of) the decision threshold.

Unlike the SAT studies reviewed above – which contrast response time, accuracy and neural activity during instructed speed emphasis with that during instructed accuracy emphasis – the current fMRI study used the Response Signal Method [RSM, 9] to systematically vary response speed in a bottom-up manner in order to address the question: is the SAT driven by one or several neural mechanisms? [1]. The RSM was specifically developed to examine aspects of the SAT that cannot be attributed to top-down control [9] and has been the focus of a large number of SAT studies [e.g. 9–19]. The RSM permits the experimenter to impose a SAT by explicitly signaling the end of the retrieval process with the offset of the probe. Prompt recognition responses are then acquired following a number of different probe durations (i.e. response speeds). The presence of a SAT in this context is designated by increased accuracy following longer probe durations and decreased accuracy following shorter probe durations. SAT functions can also be generated by plotting recognition performance as function of total processing time: response time plus probe duration – as response speed is typically not completely controlled across probe durations. The current fMRI study used the RSM to systematically vary response speed in a delayed item recognition (DIR) task to determine if the SAT is driven by one or several neural mechanisms.

During each trial in this DIR task, 26 young individuals (M age = 25.88) were presented with two abstract shapes for 3,000 ms. After a 5,000 ms retention period, individuals were presented with a probe shape and asked to decide whether or not it matched one of the two previously presented shapes. The duration of the probe shape was systematically varied (125, 250, 500, 1,000 or 2,000 ms.) and participants were trained to elicit a recognition response following presentation of the probe shape at the onset of a 500 ms gray mask. Individuals were trained to emphasize speed, and to guess rather than delay their responses if unsure. This DIR task consisted of 11 blocks of 30 trials each, divided into three training phases and one test phase. Within each block, 70 blanks that lasted for 2,000 ms were also randomly interspersed. When added to the minimum inter-trial interval (ITI) of three seconds, the mean ITI was 9119 ms. These design features are known to maximize the statistical power in fMRI analyses [20, 21] (see [12] for a detailed description of this DIR task). Note that the young sample included in the current study was obtained from a larger study specifically aimed to determine whether the expression of networks associated with performance on this DIR task differ as a function of response speed in younger and older adults [22]. The analytic approach used in the current study differed as well (see below).

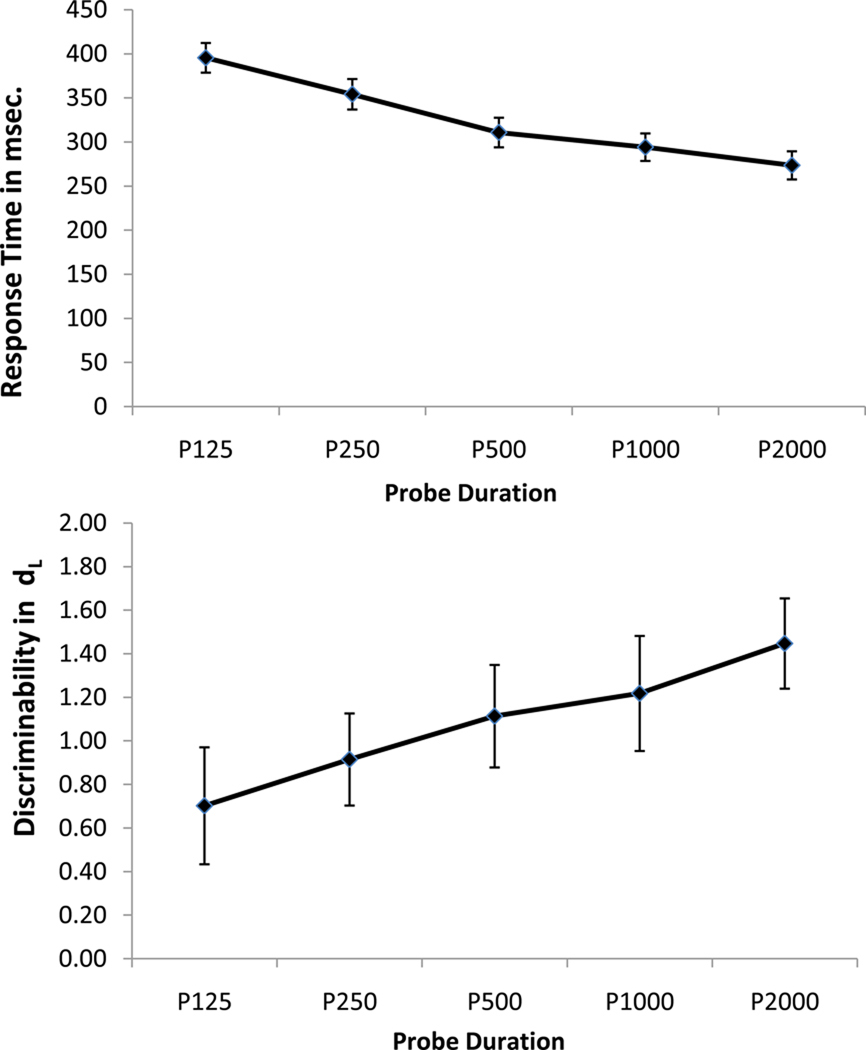
Response time (RT) and accuracy were analyzed in two separate repeated-measures ANOVAs with probe shape duration (125, 250, 500, 1,000 and 2,000 ms) as the within-subject factor. RT was measured from the onset of the mask (i.e. excluding the systematic variation in response time that was enforced by different probe shape durations) and accuracy was measured in terms of discriminability, assessed with d_L = ln{[H(1 − FA)]/[(1 − H) FA)]}; where H = hits, FA = false alarms, and ln is the natural logarithm function [23]. RT increased with decreasing probe shape duration, F (4, 100) = 148.41, p <.001 (see Figure 1a), suggesting that response times were not completely controlled by our RSM manipulation. More importantly, for the current purposes, d_L increased with increasing probe shape duration, F (4, 100) = 15.53, p <.001 (see Figure 1b), consistent with the presence of a SAT. Note also that unlike the larger study [22] from which the current sample was obtained – which modeled the SAT between total processing time (probe shape duration and reaction time) and discriminability (d_L) with a three-parameter bound exponential curve (intercept, asymptote and rate) in younger and older adults) – the current study examined discriminability (d_L) simply to confirm the presence of a SAT in younger adults.

Figure 1.

a. Response time as a function of probe shape duration.

b. Discriminability as a function of probe shape duration.

All BOLD (T2^*- weighted) images [24, 25] were acquired during the DIR task with an Intera 1.5 T Phillips MR scanner equipped with a standard quadrature head coil and a GE-EPI sequence of TE/TR = 50 ms/3000 ms; flip angle = 90 degrees; 64 × 64 matrix, in-plane voxel size = 3.124×3.124 mm; slice thickness = 8 mm (no gap); 17 trans-axial slices per volume. Four additional GE-EPI excitations were performed before each run to allow transverse magnetization immediately after radio-frequency excitation to approach its steady-state value; the image data for these excitations were discarded. A T1-weighted spoiled gradient image was also acquired from each participant (TE/TR = 3ms/25ms; flip angle = 45 degrees, 256 × 256 matrix; in plane voxel size = 0.781×0.781 mm; slice thickness = 1.5 mm [no gap]; 124 trans-axial slices per volume).

Image pre-processing and analysis were implemented with SPM5 (Wellcome Department of Cognitive Neurology) and custom-written MATLAB 7.8 code (Mathworks, Natick, MA). For each participant's EPI dataset: data were temporally shifted to correct for the order of slice acquisition, using the first slice acquired in the TR as the reference and then realigned to the first volume of the first session. The high-resolution T1-weighted (structural) image was co-registered to the first EPI volume using mutual information [26]. The co-registered structural image was used to determine the linear and non-linear parameters for transformation defined by the Montreal Neurologic Institute template brain supplied with the software. This transformation was then applied to the EPI data and re-sliced using sinc-interpolation to 2×2×2 mm voxel sizes. Finally, images were spatially smoothed with an isotropic Gaussian kernel, full-width-at-half-maximum = 8 mm.

The fMRI data time-series analysis consisted of two levels of voxel-wise General Linear Models (GLMs) [27]. The first-level GLM yielded the summary measures used in second-level group-wise analysis (beta images), which affords statistical inference at the population level. In the first-level GLM, the EPI time-series data were modeled with regressors representing the expected BOLD response (implicitly, relative to blanks) to the DIR components: shape presentation, retention period, and probe shape duration/response. Shape presentation and retention period were each modeled with a single regressor. For the probe shape duration and response/mask, each crossing of probe-duration and true positive/true negative factors were separately modeled. The regressors were constructed by convolution of a rectangular function of width defined by the design, to represent each trial component [28] and the double-Gamma model of the BOLD response function. Resulting contrast images for the five probe durations combined with their respective response masks were used in the second-level group GLM analyses.

Group-level imaging analyses focused on identifying spatially covarying sets of brain regions whose neural activity increase and/or decrease as a function of probe shape duration. A covariance-based analytic approach – Multivariate Linear Modeling (MLM) [29, 30] – was used to test for the presence of spatial patterns of covarying neural activity that are activated at each level of probe shape duration. Moreover, the MLM approach directly tests whether one or more of these patterns are elicited at different points across the SAT function, i.e. whether one or several neural mechanisms underlies the SAT. Note also that the number of spatial patterns that can be identified with this analytic approach is determined by the dimensionality of the F-contrasts. The current contrasts of interests have a dimensionality of five (one for each probe shape duration) and therefore the largest number of significant spatial patterns is five. The MLM analysis performed a principle components eigendecomposition on the spatially whitened mean images for the five probe shape durations. Significance of a spatial pattern was assessed using sequential latent root tests and an alpha < .05. Three significant spatial patterns were found (Pattern 1: F(2978, 17010) = 3.2068, p < 0.0001; Pattern 2: F(2383, 15879) = 1.6399, p < 0.0001; Pattern 3: F(1787, 14295) = 1.2455, p < 0.0001). For interpretation of brain regions, from each significant spatial pattern the top 2% of the values and clusters greater than 20 voxels in size were retained and are shown in Figure 2 and listed in Tables 1. Finally, note that this analytic approach differs markedly from the analytic approach used in the larger study from which this sample was obtained [22] whose contrasts of interest have a dimensionality of two (one for each age group) and therefore the largest number of significant spatial patterns that could be identified in that study was two.

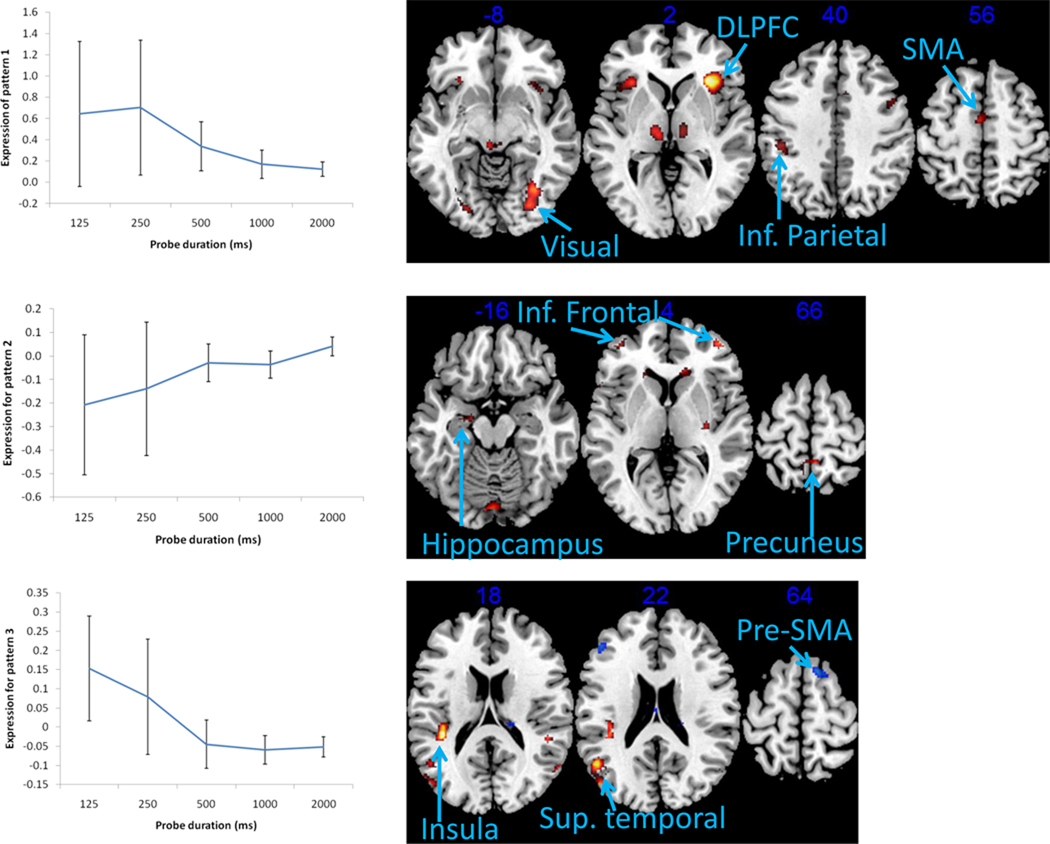
Figure 2.

a. Mean expression of Pattern 1 as a function probe shape duration, and the primary brain regions associated with this pattern.

b. Mean expression of Pattern 2 as a function probe shape duration, and the primary brain regions associated with this pattern.

c. Mean expression of Pattern 3 as a function probe shape duration, and the primary brain regions associated with this pattern.

Table 1. Brain regions associated with each significant spatial pattern.

The top 2% of the values clusters greater than 20 voxels in size were retained

Regions	Laterality	BA	MNI	Z	# voxels
Pattern 1 Positive activation
SMA	L	6	−2, −8, 56	7.58	102
Postcentral gyrus/Inferior parietal lobule	L	2/40	−44,−30, 40	7.17	134
Cingulate gyrus	R	32	10, 16, 38	6.61	20
Inferior frontal/Precentral gyrus	L	6/9	−42, 8, 24	7.24	283
Superior temporal gyrus	R	42	58, −44, 16	8.05	158
Inferior/middle frontal gyrus	R	9/46/47	32, 26, 2	10.21	1143
Inferior frontal gyrus/Insula	L	13/47	−30, 24, −2	8.65	279
Thalamus	L/R	na	−4, −26, −6	8.37	419
Fusiform/lingual gyrus	R	18/19/37	34, −66, −8	8.41	313
Fusiform gyrus/Temporal lobe	L	18/19/37	−34, −54, −14	7.48	56
Pattern 2 Positive activation
Precuneus	L/R	7	4, −46, 66	5.45	91
Inferior parietal lobule	R	40	46, −60, 42	5.95	336
Middle frontal gyrus	R	8	28, 18, 38	4.82	42
Superior temporal/supramarginal gyrus	L	39/40	−40, −56, 32	6.99	927
Caudate	L	na	−20, 20, 14	6.56	325
Caudate	R	na	18, 18, 14	5.09	211
Superior frontal gyrus	R	10	14, 66, 12	5.28	62
Putamen	L	na	−26, −4, 10	4.91	110
Putamen	R	na	32, −16, 0	4.92	154
Inferior/middle frontal gyrus	L/R	10	42, 52, 4	5.46	113
Inferior frontal gyrus/Insula	L	47	−54, 18, −2	6.43	30
Middle occipital gyrus	L	19	−54, −62, −12	4.76	21
Hippocampus	L	na	−18, −10, −16	4.65	55
Cerebellum	L/R	na	−2, −84, −18	5.57	163
Cerebellum	R	na	38, −78, −24	6.71	48
Pattern 2 Negative activation
Lingual gyrus	R	18/19	30, −76, −10	5.02	87
Pattern 3 Positive activation
Superior frontal gyrus	R	8	24, 38, 48	4.06	48
Angular gyrus	R	39	50, −70, 32	4.09	37
Superior temporal gyrus	L	39	−48, −58, 22	4.39	334
Insula	L	13	−38, −34, 18	4.67	168
Insula	R	13	48, −38, 16	3.92	47
Superior temporal gyrus	R	22	48, −4, 4	4.21	44
Superior temporal gyrus	L	41	−44, −32, 0	3.95	23
Pattern 3 Negative activation
Pre-SMA	R	6	14, 16, 64	4.12	74
Precuneus	R	7	6, −64, 58	3.57	76
Superior parietal lobule	R	7	28, −64, 58	4.49	265
Superior parietal lobule	L	7	−24, −68, 56	4.86	103
Inferior parietal lobule	R	40	52, −38, 54	4.93	378
Inferior parietal lobule	L	40	−40, −52, 50	5.57	726
Medial frontal gyrus	R	8	2, 28, 44	3.67	27
Middle frontal gyrus	R	8/9	50, 28, 36	2.89	52
Middle frontal gyrus	L	46	−46, 38, 26	4.27	74
Cingulate gyrus	L	23	0, −14, 26	4.33	91
Caudate tail	R	na	18, −26, 18	3.55	28
Superior temporal gyrus	R	38	50, 14, −10	4.44	39
Fusiform gyrus	R	19/37	44, −72, −16	4.00	106
Middle Occipital Gyrus	L	37	−46, −70, −12	3.77	47

Mean expression of Pattern 1 decreased with increasing probe shape duration, but remained positive across all five levels (see Figure 2a). Pattern expression measures the extent to which each subject expresses the pattern, at each level of probe shape duration. Positive pattern expression across all levels suggests that the pattern is expressed in the same direction. Thus, this neural network is involved to a greater extent when probe shape durations are short (more speed emphasis) and to a lesser extent when probe shape durations are long (less speed emphasis). The regions with the highest values in Pattern 1 include the Inferior frontal gyrus (BA 9/47), the Middle frontal gyrus (BA 46), the precentral gyrus (BA 6), the Inferior parietal lobule (BA 40), bilateral Lingual gyrus (BA 18) and Fusiform gyrus (BA 19). In contrast with previous fMRI studies of the SAT [6–8], the pre-SMA was not a component of this neural network that likely activates for speeded responses. Instead, motor preparatory (the SMA and pre-motor) areas is a main component of this network. However, in line with one previous fMRI study of the SAT [8], the dorsolateral prefrontal cortex (DLPFC; BA 9/47, 46), is also a component of this neural network that likely activates for speeded responses. Moreover, the identification of this spatial pattern implies interplay between these frontal/prefrontal regions, visual association cortices (BA 18, 19) and the inferior parietal lobule (BA 40). Visual association cortices and the inferior parietal lobule have been specifically linked to simple storage of non-verbal information in working memory tasks such as the DIR task [31].

In contrast to Pattern 1, Patterns 2 and 3 were expressed in opposing directions with increasing probe shape duration, crossing from negative to positive and vice versa, respectively. Pattern expression values can be positive or negative and brain areas in a pattern can have positive and negative weightings. The regions with positive weightings were activated for positive pattern expression values and deactivated for negative expression values, and the converse is true for the regions in the negative side of the pattern (analogous to the multiplication rule of positive and negative values).

Pattern 2 increased from −0.21 at the shortest probe duration to +0.04 for the longest probe duration (see Figure 2b). The regions in the positive side of Pattern 2 included the Inferior frontal gyrus (BA 10), the Precuneus (BA 7), the Inferior parietal lobule (BA 40), the Hippocampus, the Putamen, and parts of the Cerebellum. These regions were deactivated during shorter probe durations, but the expression was increased across the levels until the regions were weakly activated at the longest probe shape duration. Thus, the positive side of this neural network was deactivated when probe shape durations were short (more speed emphasis) and activated when probe shape durations were long (less speed emphasis). This suggests that pattern 2 represents a neural network more tied to accuracy rather than to speeded responses. The inferior frontal gyrus has been specifically linked to manipulation of information in working memory tasks such as the DIR task, while the precuneus has been linked to executive control processes in general [31]. The hippocampus plays a critical role in long-term memory formation but has also been linked to spatial processing such as the construction of mental images [32–34]. The negative side of Pattern 2 only included the Lingual gyrus (BA 18/19) and was activated for the four shortest probe durations but decreased expression until it was deactivated at the longest probe duration. Like Pattern 1, this spatial pattern implies that interplay between different brain regions likely underlie the SAT – in this case: frontal/prefrontal, medial-temporal, and occipital regions.

Pattern 3 expression means followed the opposite trend from Pattern 2 expression means: positive expression at the two shortest probe durations, decreasing to negative expression values at the three longest probe durations (see Figure 2c). Specifically, the expression means for Pattern 2 decreased from +0.15 at the shortest probe shape duration to −0.05 for the longest probe shape duration (see Figure 2c). The regions in the positive side of Pattern 3 included the Superior temporal gyrus (BA 22/39) and the Insula (BA 13), and were activated during the two shortest probe durations and deactivated during the three longest probe shape durations. The regions in the negative side of Pattern 3 include the Middle frontal gyrus (BA 8/9), the Pre-SMA (BA 6), Superior parietal lobule (BA 7), Inferior parietal lobule (BA 40), the Precuneus (BA7), and the fusiform gyrus (BA 19). These regions were deactivated during the two shortest probe durations and activated during the three longest probe shape durations. The Pre-SMA have been specifically linked to speeded responses in previous fMRI studies of the SAT [6–8], but in the current study it appears to be linked to accurate rather than speeded responses. The middle frontal gyrus have been specifically linked to updating (adding and deleting information) in working memory tasks such as the N back task and the DIR task, while the superior parietal lobule and the precuneus have been linked to executive functions in general [31, 35]. The identification of this spatial pattern also implies that interplay between different brain regions likely underlie the SAT – in this case: frontal/prefrontal, medial-temporal, parietal, and occipital.

In sum, the current study used the RSM to systematically vary response speed and address the question: Is the SAT driven by one or several neural mechanisms? A covariance-based MLM approach identified three distributed neural networks that varied as a function of probe shape duration, indicating that the SAT (when manipulated in this bottom-up manner) is driven by three neural mechanisms that are highly distributed across brain regions. The first neural network included the SMA, the DLPFC, visual association cortices, and the inferior parietal lobule. This neural network is linked to speeded responses because it was more activated during short probe durations than during long probe durations. In contrast to previous fMRI studies of the SAT, this speeded response network did not include the pre-SMA [6–8], most likely because our RSM paradigm minimized top-down influence on speed to a greater extent than previous paradigms. In other words, while participants in previous studies were instructed to vary their performance in favor of speed or accuracy during specific blocks or trials, participants had no advance knowledge of response time (i.e. probe duration) from trial to trial in the current study. The second neural network is linked to accurate responses, as it was primarily deactivated during short probe durations but activated during long probe durations. The inferior frontal gyrus, the precuneus, and the hippocampus were the main components of this neural network, and implies that this network is linked to accuracy by actively manipulating the previously presented shapes and constructing mental images that can later be stored, or transferred, to long term memory [32–34]. One component (including the superior temporal gyrus and the insula) of the third neural network was active during the short probe shape durations and deactivated during the long probe shape durations while another component (including the pre-SMA and the middle frontal gyrus) of the third neural network was deactivated during the short probe durations and activated during the long probe shape durations. In other words, one component activated for speeded responses while the other component deactivated for accurate responses. The latter involved the pre-SMA and the middle frontal gyrus, implying that this portion of network three may be involved in updating information across trials [31]. Taken together, this covariance-based analytic approach to fMRI data suggest that the SAT is driven by three highly distributed neural mechanisms that are differentially activated, deactivated, or both activated and deactivated, as a function of increasing response speed with the response signal method.

Research Highlights.

This functional neuroimaging (fMRI) study examined the neural networks or spatial patterns of covarying neural activity that are associated with the speed-accuracy tradeoff (SAT) in younger adults. The response signal method was used to systematically increase probe duration (125, 250, 500, 1,000 2,000 ms) in a bottom-up manner during a nonverbal delayed-item recognition task. A covariance-based multivariate approach identified three networks that varied with probe duration – indicating that the SAT when operating in a bottom-up manner is driven by three distributed neural networks.