Table IV.

Population Pharmacokinetic Parameters of the Parent Drug and Its Active Metabolite for the Model Without and With the Genetic Covariate

	Without the genetic covariate		With the genetic covariate
	(N = 101)		(N = 99)
f	1.00	–	1.00	–
β f,D a (nmol−1)	−0.02	28	−0.02	24
F ap	0.85	2	0.87	2
β Fp,D a (nmol−1)	−0.04	29	−0.06	27
K a (h−1)	8.06	–	8.06	–
V a (L)	19.2	4	19.4	5
CL apo (L h−1)	0.84	11	0.67	11
CL apm (L h−1)	1.94	5	2.09	5
CL amo (L h−1)	0.46	6	0.50	7
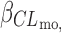CY P 2D6 a (log(L h−1))	−	−	−0.42	40
CL amp (L h−1)	0.09	12	0.09	12
ω f a	0.25	13	0.27	12
ω Ka a	1.50	21	1.41	25
ω V a	0.19	18	0.26	13
ωCL apo	0.52	29	0.46	38
ωCL amo	0.51	8	0.50	8
γCL apo	0.79	12	0.82	12
b p	0.31	3	0.30	3
a m (nmol−1)	66.9	14	66.5	14
b m	0.06	9	0.06	9

Estimates and relative standard errors (in grey,%) using the SAEM algorithm in MONOLIX and encoding in closed form

V = V _p = V _m

ω Between-subject standard deviation, γ within-subject standard deviation, a additive coefficient in nanomoles per liter, b multiplicative coefficient, a _p was fixed to 0

^aEstimates that rely on the assumption that V _m = V _p