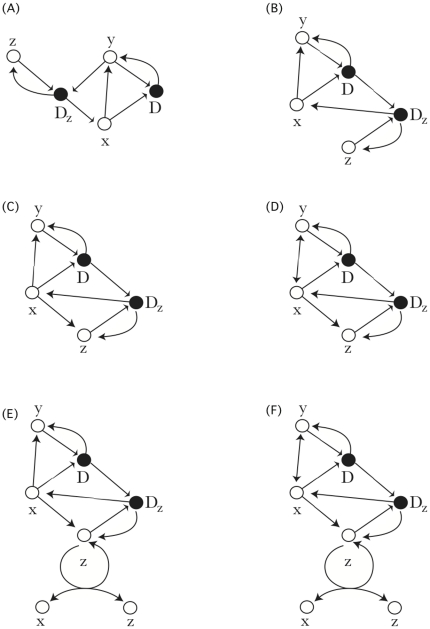
Figure 4. Conflict networks illustrated as reaction graphs.
Open nodes are single individuals. Closed nodes are groups of 2 or more individuals. Directed edges represent transformations but not stoichiometry. Merging input edges into a single closed node corresponds to the formation of a complex (dyad or triad). Cycles represent transformations that yield one starting state and one alternative. The six conflict networks are: (A) B-cell inspired pacification. (B) T-cell inspired policing. (C) Spontaneous policing. (D) Temporary aggression. (E) Conditional Policing. (F) Conditional, Temporary Policing. Hence in (A) 
becomes aggressive and transforms to 
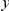. The aggressive individual 
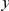interacts with 
to form a fight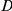 
which then resolves into aggressive individuals 
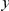. The strategy 
interacts with 
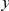to form the pacifying dyad 
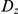which then resolves into 
and 
. In the most complicated example (F), 
becomes aggressive and transforms to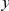 
, and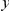 
can revert to 
. The aggressive individual 
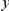interacts with 
to form a fight 
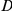which then resolves into aggressive individuals 
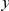. The strategy 
can spontaneously transform into 
. The strategy 
can interact with 
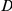to form the triadic complex 
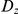, which resolves into 
and 
. he strategy 
can spontaneously transform into 
.