Fig. 1.
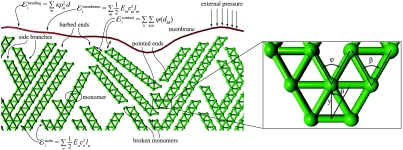
The model. We consider a two-dimensional network of actin filaments growing against a membrane subject to an external force F directed along the protrusion direction y and opposing the lamellipodium growth. Actin monomers are modeled, as in a truss structure, by two nodes and four connections (edges, the green lines in the figure). Lengths are measured in units of the filament thickness d and forces in units of the filament rupture force Fr. The force F is distributed on a representative cell of width Lcell = 32 d. Periodic boundary conditions are assumed in order to reduce edge effects. At the beginning of the simulation, 12 monomers are created at y ∼ 0 at an angle θ with the y axis. These seeds are kept fixed throughout the simulation. Time is measured in units of growth steps, in each of which a monomer is added at the tip (barbed end) of a randomly chosen filament. One branching event occurs at a random site along the filaments at every growth step with a probability Pb = 0.3. The branching angle φ is fixed at 60° [close to the measured value of 70° (6, 11, 12)]. The contact among different filaments and between filaments and the membrane is modeled by a short-range repulsive potential active for a distance < d. In view of the truss geometry, filaments fail if the absolute value of the force in one of the edges exceeds a critical value fc = Fr/2, in which case the overcritical monomer is cleaved. Cleaved filaments, which have an exposed pointed end, depolymerize with a speed of 10 monomers per growth step. We assume the filaments to be linearly elastic up to failure, with a persistence length ξ = 1,000 d. This corresponds to approximately 10 μm (35). Reduction to a two-dimensional model is obtained by assuming that a growing planar network deforms a slice of thickness d in the direction orthogonal to the plane of the lamellipodium. The resulting one-dimensional elastic membrane has stretching stiffness of the order of Fr (37) and bending stiffness κ = 0.1Frd2, which results in a persistence length λd with λ ∼ 8 ≪ 103 (4, 12). The influence of the parameters on the predictions of the model is discussed in detail in SI Text.