Detailed Analysis for the Solvolysis of Isopropenyl Chloroformate

Abstract

The specific rates of solvolysis (including those obtained from the literature) of isopropenyl chloroformate (1) are analyzed using the extended Grunwald-Winstein equation, involving the N_T scale of solvent nucleophilicity (S-methyldibenzothiophenium ion) combined with a Y_Cl scale based on 1-adamantyl chloride solvolysis. A similarity model approach, using phenyl chloroformate solvolyses for comparison, indicated a dominant bimolecular carbonyl-addition mechanism for the solvolyses of 1 in all solvents except 97% 1,1,1,3,3,3-hexafluoro-2-propanol (HFIP). An extensive evaluation of the outcomes acquired through the application of the extended Grunwald-Winstein equation resulted in the proposal of an addition-elimination mechanism dominating in most of the solvents, but in 97-70% HFIP, and 97% 2,2,2-trifluoroethanol (TFE), it is proposed that a superimposed unimolecular (S_N1) type ionization is making a significant contribution.

1. Introduction

The two-term extended [1] Grunwald-Winstein equation was found to be very efficient [2] in correlation studies for elucidating solvolytic mechanisms of reaction for a variety of chloroformate esters (ROCOCl) [2–28], and their corresponding sulfur-for-oxygen substituted analogs (RSCOCl, ROCSCl and RSCSCl) [2,23,26,29–34]. In the extended (equation 1) Grunwald-Winstein equation [1], k and k_o are the specific rates of solvolysis in a given solvent and in the standard solvent (80% ethanol), respectively, l governs the sensitivity to changes in solvent nucleophilicity (N), m represents the sensitivity to changes in the solvent ionizing power Y (initially set at unity for tert-butyl chloride solvolyses), and c is a constant (residual) term [2].

$$\text{log}(k/k_o)=lN+mY+c$$ (1)

N_T scales based on the solvolyses of the S-methyldibenzothiophenium ion [35,36] have now become the recognized standards for considerations of solvent nucleophilicity and it has been previously show [37,38] that adamantyl derivatives provide better standard substrates for a leaving group X. Hence a series of Y_X scales [37–43] are now available. Whenever the reaction center is adjacent to a π-system [44,45], or in α-haloalkyl aryl compounds that proceed via anchimeric assistance (k_Δ)[46], Kevill and D’Souza recommended [2,47–50] the addition of an additional aromatic ring parameter (hI) term to equation 1 give equation 2. In equation 2, h represents the sensitivity of solvolyses to changes in the aromatic ring parameter I.

$$\text{log}(k/k_o)=lN+mY+hI+c$$ (2)

Due to increased initial resonance ground state-stabilization [26,51–56], chloroformate esters were found to be much less reactive than acyl chlorides. Hence, they are widely employed [57,58] as precursors to produce commercially useful pharmaceutical and agricultural products. Lee’s original proposal [59] of the existence of a syn geometry in haloformate esters was confirmed [55,60–66] in recent computational and experimental studies and crystal structure analysis. In Figure 1, s-isopropenyl chloroformate (1, i-PropenylOCOCl), s-isopropyl chloroformate (2, i-PrOCOCl) and s-phenyl chloroformate (3, PhOCOCl) are shown with the halogen atom in a trans position to the alkenyl, alkyl or aryl group, i.e. in syn-geometry.

Figure 1.

Molecular structures of s-isopropenyl chloroformate (1), s-isopropyl chloroformate (2), and s-phenyl chloroformate (3)

Since World War I there has been significant interest in 1 due to its ability to cause sharp pain in the eyes upon exposure to the evaporating gas [67]. In 1915, phosgene was first employed [67] as a war gas because it was claimed to readily dissolve in acetone to form 1, which then underwent rapid hydrolysis to produce corrosive HCl (Scheme 1). However, this enol acylation could not be reproduced and has since been disproved [68].

Scheme 1.

Acylation of the enol form of acetone with phosgene to produce 1.

Recent applications [69] of 1 include its use in the synthesis of protective groups for amino acids and peptides. Ryu and coworkers [22] using equation 1, analyzed the kinetic data of 1 in 40 solvents of varying nucleophilicity and ionizing power at 10.0°C, its kinetic solvent isotope effects (KSIE) in methanol and water, and after studying the previously reported data on steric effects [51–53], proposed a third order reaction mechanism with four competing reaction-channels in the aqueous alcohol solvent systems. Koh and Kang [70] recently proposed that 1 undergoes solvolysis by a rate-limiting addition in an addition-elimination pathway coupled with general base catalysis being superimposed upon the bimolecular process.

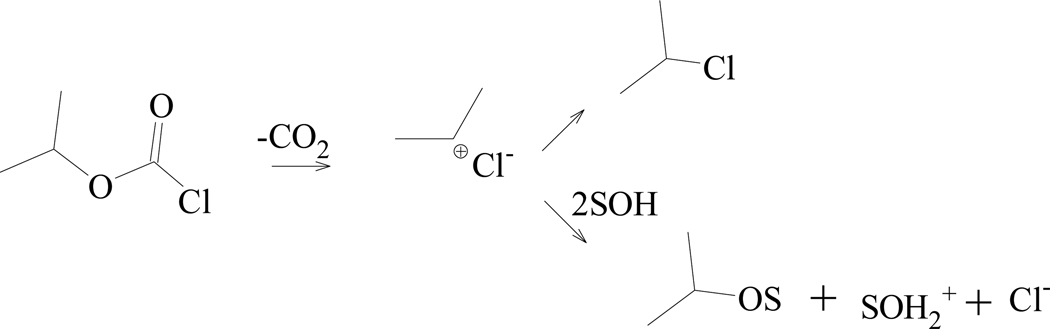
On the other hand dissecting the data obtained from extensive correlation analysis [17,27] results using equation 1, for 1’s alkyl analog isopropyl chloroformate (i-PrOCOCl, 2), the observed [15,27,61] k₂/k_i-PrOCOF rate ratio, and a consideration of a previously reported KSIE value [51] of 1.25 in water, it was shown [27] that 2 solvolyzes by dual channels; with an addition-elimination pathway being dominant in the more nucleophilic solvents and a fragmentation-ionization mechanism (Scheme 2) proceeding in the strongly hydrogen-bonding (ionizing) fluoroalcohols.

Scheme 2.

Solvolysis-decomposition of s-isopropyl chloroformate (2)

Replacement of the ether oxygen in 2 with sulfur yields isopropyl chlorothioformate (i-PrSCOCl), that was recently shown [34] to solvolyze by a dominant stepwise S_N1 mechanism with moderate rear-side nucleophilic solvation of the developing acylium ion. This conclusion [34] for a dominant unimolecular pathway for i-PrSCOCl in all solvents except 100% EtOH, occurred with no alkyl-sulfur bond fission. This proposal resulted from a consideration that Queen et al. [52] found 2-propanethiol as the only product in the hydrolysis of i-PrSCOCl, the interpretation of the results obtained from the correlation analysis of its specific rates of solvolysis using equation 1, and the responses of the RSCOCl/ROCOCl rate ratios to changes in the R group.

Phenyl chloroformate (3, PhOCOCl) is well established [2–34] as undergoing solvolysis proceeding by the addition-elimination (tetrahedral intermediate) type mechanism with the addition step being rate-determining. The observed [9,23] l and m values of 1.66 and 0.56 respectively for 3 using equation 1, are now recommended as standard sensitivities [2] for attack at an sp² carbon (acyl) proceeding by the addition-elimination (association-dissociation) mechanism. Replacing both electronegative oxygens in 3 with a more electropositive sulfur yields phenyl chlorodithioformate (PhSCSCl), that was recently shown [23,30] to solvolyze by a dominant stepwise unimolecular pathway (S_N1) in all of the solvents studied. Using equations 1 and 2, large sensitivities [23,30] for solvent nucleophilicity l of 0.69 and 0.80 were obtained, and values of 0.95 and 1.02 were acquired for m. Furthermore, with equation 2 an h value of 0.42 ± 0.15 signified that there was minimal charge dispersion into the aromatic ring during the formation of the thioacylium transition state that was stabilized by intense rear-side nucleophilic solvation (as indicated by the large l value). These sensitivity values are now considered typical [2,7,23,27,29,30,33,34,49,56] for substrates believed to solvolyze with the formation of an acylium or a thioacylium ion in the transition state.

The simplest alkyl chloroformate, methyl chloroformate [14], was believed to solvolyze by a dominant bimolecular pathway (addition-elimination) in all solvents except 90% HFIP, where a superimposed ionization channel was proposed. Superimposed mechanisms are also observed in a wider range of solvents for ethyl [12], n-propyl [20], and n-octyl [18] chloroformate esters.

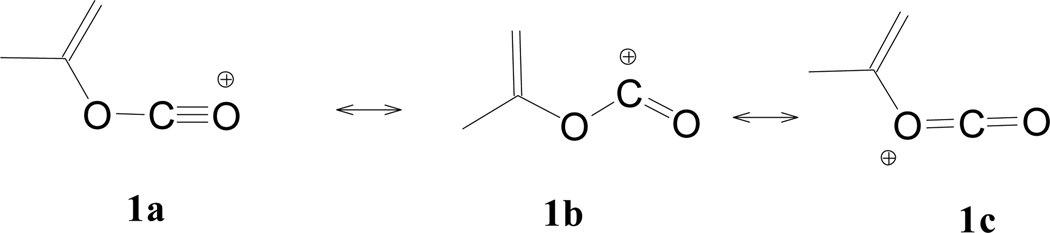
In theory, it should be possible for 1 to undergo solvolytic displacement in a stepwise unimolecular (S_N1) fashion with the formation of a resonance stabilized sp-hybridized acylium ion intermediate (Scheme 3). Also, it was demonstrated [2,12,14,15,18,20,21,23–27] that dual reaction channels occurring simultaneously in a side-by-side fashion are possible in some alkyl and aryl chloroformate esters, and that the highly ionizing aqueous 2,2,2,-trifluoethanol (TFE) and 1,1,1,3,3,3,-hexafluoro-2-propanol (HFIP) mixtures are shown [2,3,6–49,55,56,71–74] to be extremely important for meaningful treatments leading to analyses using the Grunwald-Winstein equations. To probe the possibility of an ionization pathway for 1, we have raised the temperatures (so that the kinetic runs could be followed within a reasonable time frame) and in Table 1 have included 16 specific rates of solvolysis in six solvents with strong hydrogen bonding (highly ionizing) fluoroalcohol components. Additionally in Table 1, we report the Arrhenius activation parameters (ΔH^≠, ΔS^≠) at 25.0°C for 5 of the fluoroalcohol mixtures studied, and a further eight additional specific rates of solvolysis in aqueous alcohols.

Scheme 3.

Possible resonance state intermediates for the isopropenyl chloroformate carbocation.

Table 1.

Specific rates of solvolysis (k) of 1, in several pure and binary solvents at 10.0°C, 25.0ºC, 45.0°C, 55.0°C, and 65.0°C.

Solvent (%)a	1 @ 10.0°C; 105k, s−1b	1 @ 25.0°C; 105k, s−1b	1 @ 45.0°C; 105k, s−1b	1 @ 55.0°C; 105k, s−1b	1 @ 65.0°C; 105k, s−1b
100% MeOHc	69.2 ± 3.7	210 ± 8
90% MeOHd	146 ± 5
80% MeOHe	149 ± 7
100% EtOHf		110 ± 6
90% EtOHg	45.6 ± 2.2
80% EtOHh	49.8 ± 1.3
97% TFE (w/w)i	0.0242j		0.173 ± 0.023	0.483 ± 0.009
90% TFE (w/w)	0.102 ± 0.049
97%HFIP (w/w)k	0.00914l			0.301 ± 0.018	0.537 ± 0.003
90%HFIP (w/w)m	0.0553n		0.705 ± 0.023	1.29 ± 0.13	2.37 ± 0.25
70%HFIP (w/w)o	0.532p	2.54 ± 0.09	20.5 ± 3.0	38.4 ± 1.2
50% HFIP (w/w)q	18.5r	35.2 ± 3.1	65.2 ± 2.1	105 ± 12

^aSubstrate concentration of ca. 0.0052 M; binary solvents on a volume-volume basis at the temperature studied, except for TFE-H₂O and HFIP-H₂O solvents which are on a weight-weight basis. T-E are TFE-ethanol mixtures.

^bWith associated standard deviation.

^cA value of 74.0 (± 0.6) X10⁻⁵ s⁻¹ is reported in ref. 22.

^dA value of 127 (± 3) X10⁻⁵ s⁻¹ is reported in ref. 22.

^eA value of 158 (± 3) X10⁻⁵ s⁻¹ is reported in ref. 22.

^fA value of 72.3 (± 2.1) X10⁻⁵ s⁻¹ was obtained at 21.0°C.

^gA value of 39.2 (± 0.05) × 10⁻⁵ s⁻¹ is reported in ref 22.

^hA value of 46.8 (± 0.03) × 10⁻⁵ s⁻¹ is reported in ref. 22.

ⁱA value of 0.0856 (± 0.005) × 10⁻⁵ s⁻¹ was obtained at 35.0 °C. ΔH^≠ = 16.7 kcal/mol, ΔS^≠ = −32.1 cal mol⁻¹ K⁻¹ at 25.0°C.

^jValue calculated using Arrhenius equation.

^kA value of 0.199 (± 0.006) × 10⁻⁵ s⁻¹ was obtained at 50.0 °C. ΔH^≠ = 13.5 kcal/mol, ΔS^≠ = −42.8 cal mol⁻¹ K⁻¹ at 25.0°C.

^lValue calculated using Arrhenius equation.

^mΔH^≠ = 12.4 kcal/mol, ΔS^≠ = −43.3 cal mol⁻¹ K⁻¹ at 25.0°C.

ⁿValue calculated using Arrhenius equation.

^oΔH^≠ = 17.3 kcal/mol, ΔS^≠ = −21.3 cal mol⁻¹ K⁻¹ at 25.0°C.

^pValue calculated using Arrhenius equation.

^qΔH^≠ = 6.3 kcal/mol, ΔS^≠ = −53.3 cal mol⁻¹ K⁻¹ at 25.0°C.

^rValue calculated using Arrhenius equation.

2. Experimental section

The isopropenyl chloroformate (95%, Sigma-Aldrich) was used as received. Solvents were purified and the kinetic runs carried out as described previously [9]. A substrate concentration of approximately 0.005 M in a variety of solvents was employed. For some of the runs, calculation of the specific rates of solvolysis (first-order rate coefficients) was carried out by a process in which the conventional Guggenheim treatment was modified so as to give an estimate of the infinity titer, which was then used to calculate for each run a series of integrated rate coefficients [25]. The specific rates and associated standard deviations, as presented in Table 1, are obtained by averaging all of the values from, at least, duplicate runs.

Multiple regression analyses were carried out using the Excel 2007 package from the Microsoft Corporation, and the SigmaPlot 9.0 software version from Systat Software, Inc., San Jose, CA, was used for the Guggenheim treatments.

3. Results and Discussion

The solvolytic rate constants for 1 in 100-80% MeOH, and 100-80% EtOH at 10.0°C reported in Table 1 are within the threshold of acceptable experimental error from the previously reported [22] rate values of 1 in these solvents. Additional alcoholysis values at 25.0°C were obtained for MeOH and EtOH, and one more rate constant at 21.0°C was determined for pure EtOH. Using the specific rates of solvolysis values that were obtained at several other temperatures (listed in Table 1) in 97% TFE, 97% HFIP, 70% HFIP, and 50% HFIP, we calculate and report the estimated rate constants for these solvents at 10.0°C using the Arrhenius equation. In this table, we also report a specific rate value for 90% TFE that was determined at 10.0°C. For studies in the 5 fluoroalcohols that were carried out over several temperatures we determined the Arrhenius parameters at 25.0°C and report the ΔH^≠, ΔS^≠ values in the footnotes of Table 1.

The rate constants summarized in Table 1 for the solvolyses of 1 at 10.0°C, are combined with the available literature values for the correlation analysis using equation 1 and the correlation data are reported in Table 2. The combined 51 solvents now provide for the first extensive inquiry into the possible mechanism of solvolysis of 1 over an extensive range of solvents with widely varying nucleophilicity and ionizing ability. The observed trend is for a gradual rate upturn coinciding with the increase in water content of the binary mixtures in ethanol, methanol, acetone and TFE, or an increase in ethanol content in the TFE-EtOH mixtures. In HFIP, a substantial rate surge is observed as the water content in this highly ionizing fluoroalcohol mixture increases. On the other hand in 2, the rates decrease [24] with an increase in water content in the aqueous HFIP mixtures. This signals the importance of solvent nucleophilicity in the rate-determining step of the solvolyses of 1 and since the rate trends observed for 1 are similar to those seen in the specific rates of solvolysis of 3 [9], the prediction is for a mechanism similar to the well established carbonyl addition-elimination [9,23] solvolysis for 3.

Table 2.

Correlation of the specific rates of reaction of a variety of ROCOCl substrates using the extended Grunwald-Winstein equation (equation 1).

Substrate	na	lb	mb	cc	Rd	Fe	Mechanism
3f	49	1.66 ± 0.05	0.56 ± 0.03	0.15 ± 0.07	0.980	568	A-E
MeOCOClg	19	1.59 ± 0.09	0.58 ± 0.05	0.16 ± 0.07	0.977		A-E
EtOCOClh	28	1.56 ± 0.09	0.55 ± 0.03	0.19 ± 0.24	0.967	179	A-E
	7	0.69 ± 0.13	0.82 ± 0.16	−2.40 ± 0.27	0.946	17	SN1
2i	9	1.35 ± 0.22	0.40 ± 0.05	0.18 ± 0.07	0.960	35	A-E
	16	0.28 ± 0.04	0.59 ± 0.04	−0.32 ± 0.06	0.982	176	fragmentation-ionization
n-PrOCOClj	19	0.45 ± 0.12	0.78 ± 0.09	−0.26 ± 0.11	0.960	93	SN1
1	51k	1.40 ± 0.06	0.51 ± 0.03	−0.02 ± 0.07	0.962	294
	50l	1.54 ± 0.06	0.54 ± 0.03	0.05 ± 0.06	0.968	347	A-E
1	46m	1.52 ± 0.06	0.53 ± 0.03	0.08 ± 0.06	0.971	356
3	46n	1.58 ± 0.06	0.54 ± 0.03	0.14 ± 0.06	0.970	336

^an is the number of solvents.

^bWith associated standard error.

^cThe earlier values are accompanied by standard error of the estimate.

^dCorrelation coefficient.

^eF-test value.

^fValues taken from ref. 23.

^gValues taken from ref. 14.

^hValues taken from ref. 12.

ⁱValues taken from ref. 27.

^jValues taken from ref. 20.

^kAll available solvents at 10.0°C; including the eleven listed in Table 1 plus 40 from ref. 23.

^lNo 97 HFIP.

^mTo compare with 3 in identical solvents.

ⁿTo compare with 1 in identical solvents.

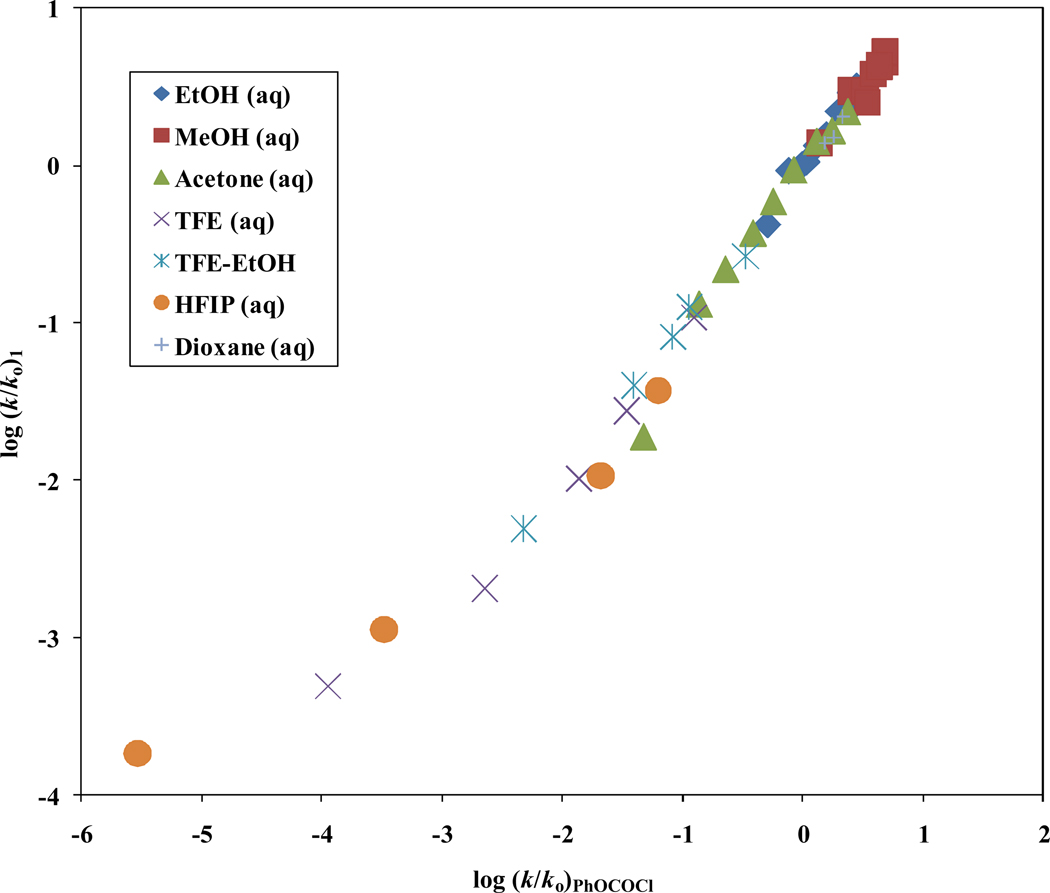
In Table 2, a comprehensive analysis using equation 1 with all 51 solvents results in a l value of 1.40 ± 0.06, a m value of 0.51 ± 0.03, R = 0.962, F-test = 294, and a c value of −0.02 ± 0.07. A plot of log (k/k_o)1 versus log (k/k_o)3 illustrated in Figure 2, points to a good linear relationship between the solvolysis of 1 and 3 in 47 common solvents, with a correlation coefficient 0.979, F-test value of 1046, a slope of 0.86 ± 0.03, and a c value of −0.04 ± 0.04.

Figure 2.

The plot of log (k/k_o) for isopropenyl chloroformate (1) against log (k/k_o) for phenyl chloroformate (3).

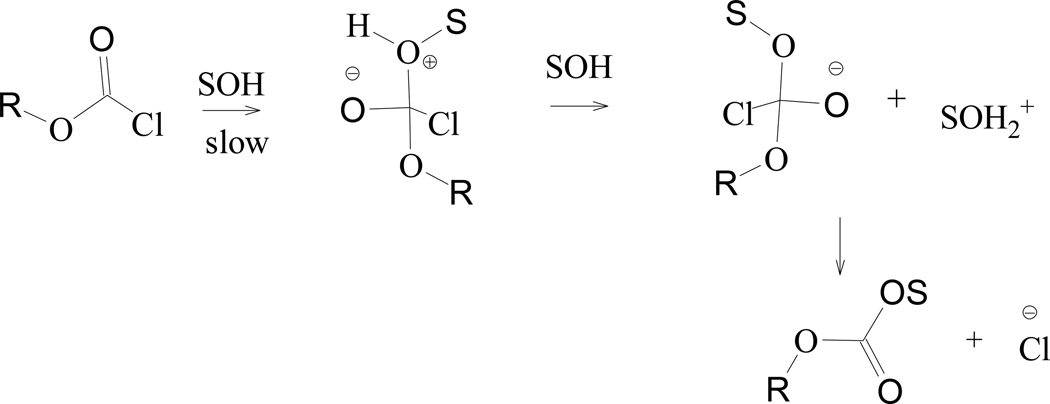
The goodness-of-fit parameters improve substantially on removal of the 97% HFIP value (46 solvents), with R = 0.991, F-test = 2298, slope = 0.95 ± 0.02, and c = −0.03 ± 0.02. Using equation 1 without the 97% HFIP value, the correlation and F-test values are improved slightly to 0.968 and 347 respectively, the l value increases to 1.54 ± 0.06, the m value is 0.54 ± 0.03, and c = 0.05 ± 0.06 for 1. Furthermore, a comparison of 1 and 3 in 46 identical common solvents yield very similar l and m values (as shown in Table 1). An examination of the l/m ratios (2.87 for 1 and 2.93 for 3) imply that the solvolyses of 1 proceeds with a likely very similar tetrahedral transition state to that observed in 3 in all solvents except 97% HFIP. The very large sensitivity (l value of 1.54) to changes in solvent nucleophilicity suggests a very pronounced involvement of the solvent as a nucleophile in the rate-determining step, consistent with the first step of an addition–elimination mechanism being rate-determining (Scheme 4).

Scheme 4.

Stepwise addition-elimination mechanism through a tetrahedral intermediate for chloroformate esters.

The relatively high k_MeOH/k_MeOD (KSIE) value reported [22] for 1 in methanol (2.33), and the k_H2O/k_D2O value of 2.08, are similar to the methanolysis KSIE values of 2.3–2.5 reported [75,76] for a series of substituted phenyl chloroformates, and a KSIE value of 1.79 for phenyl chloroformate [51] in water. These values are within the range predicted for a bimolecular solvolysis accompanied by a general base catalysis.

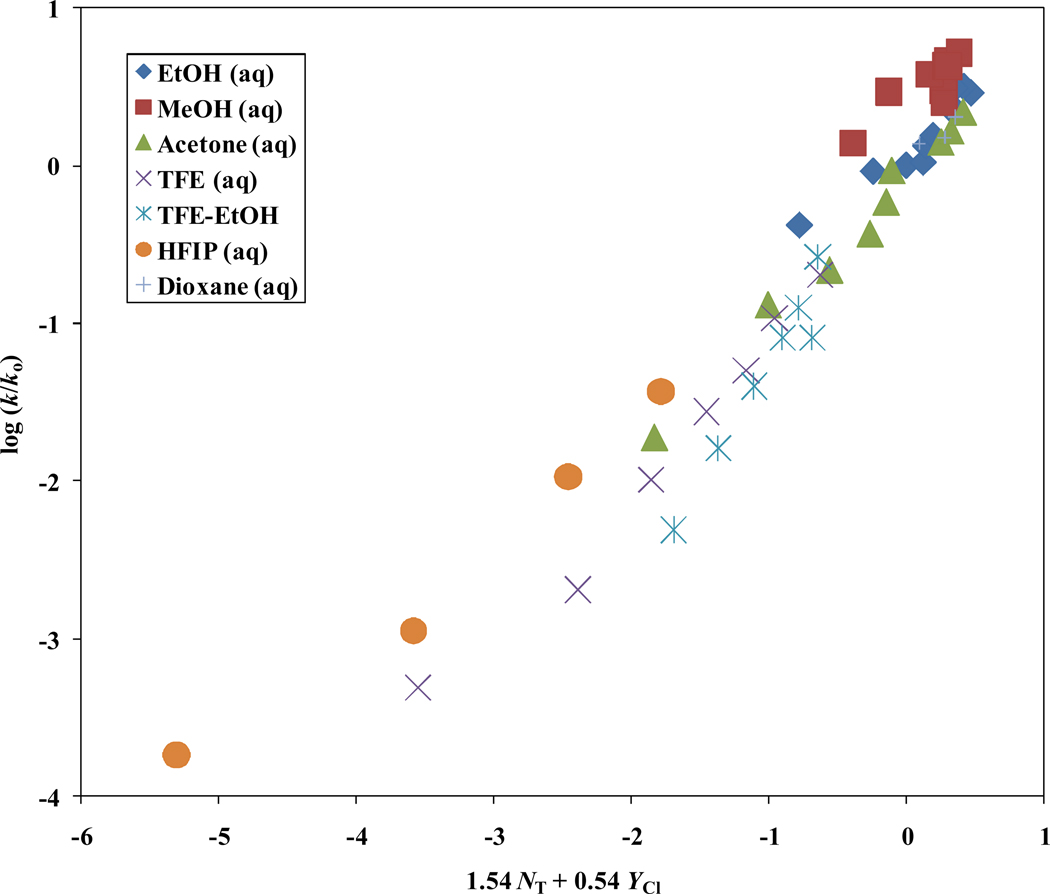
Using the equation log (k/k_o) = 1.54 N_T + 0.54 Y_Cl + 0.05 we calculate the bimolecular reaction rate constant in 97% HFIP to be 2.75 × 10⁻⁹. This value indicates that in 97% HFIP, 1 undergoes 97% of the reaction by a unimolecular ionization (S_N1) process. Using log (k/k_o) = 1.54 N_T + 0.54 Y_Cl + 0.05, the calculated bimolecular reaction rate constants for 90% HFIP, 70% HFIP, 50% HFIP, and 97% TFE, are 1.64 × 10⁻⁷, 1.94 × 10⁻⁶, 9.22 × 10⁻⁶, and 1.56 × 10⁻⁷ respectively. The corresponding % ionization values for 1 in 90% HFIP, 70% HFIP, 50% HFIP, and 97% TFE, are 70%, 64%, 5%, and 35% respectively. As shown in Figure 3, a plot of the log (k/k_o)₁ against 1.54 N_T + 0.54 Y_Cl does show these solvents deviating moderately from the line-of-best-fit.

Figure 3.

The plot of log (k/k_o) for isopropenyl chloroformate (1) against 1.54 N_T + 0.54 Y_Cl in the 51 common pure and binary solvents studied.

In Table 3, we list the specific rates of solvolysis for 1, 2, and 3, in MeOH, EtOH, 70% HFIP and 50% HFIP, four common solvents studied at 25.0°C. Observing the effect of substituent on solvolysis rates of k₃ > k₁ ≫ k₂ in MeOH and EtOH, indicates that the phenoxy group has a slightly greater electron-withdrawing character than the isopropenoxy group. Also, the rates of 1 and 3 are significantly greater than 2 in the pure alcohols where it is now proposed that all three substrates follow the addition-elimination reaction. This increase in rates is due to the noteworthy increase in inductive effects exercised by the phenoxy and isopropenoxy groups when compared to that of the isopropoxy group. In 70% HFIP and 50% HFIP the trend changes to k₂ > k₃ ≊ k₁, due to the fact that 2 solvolyses by a fragmentation-ionization mechanism [27] in the fluoroalcohols. It is well established that the vinyl cation, like the structurally related phenyl cation, is of high energy [77] and, in the absence of stabilizing factors, such as phenyl substituents [78], it will not be formed under normal solvolytic conditions [79]. Hence the favored ionization-fragmentation pathway frequently followed for 2 is not operative in the solvolyses of either 1 or 3. A comparison of k₃ and k₁ in the two HFIP mixtures shows a much closer range in their specific rates as the inductive ability of the isopropenoxy group is now opposed by the conjugative mesomeric electron release of the contributing resonance hybrids shown in Scheme 3, and as has been indicated above, there are superimposed mechanisms occurring in 70% and 50% HFIP.

Table 3.

Specific rates of solvolysis (k) of 1, 2, and 3, in MeOH, EtOH, 70%HFIP (w/w), and 50% HFIP (w/w) at 25.0ºC.

Solvent (%)a	1, 105k, s−1b	2, 105k, s−1c	3, 105k, s−1d
100% MeOH	210 ± 8	4.19 ± 0.10	695 ± 9
100% EtOH	110 ± 6	1.09 ± 0.04	260 ± 3
70%HFIP (w/w)	2.54 ± 0.09	60.1 ± 2.4	10.5 ± 0.6
50% HFIP (w/w)	35.2 ± 3.1	71 ± 3.0	31.6 ± 0.6

^a,bSee footnotes in Table 1.

^cRef. 27.

^dRef. 9.

4. Conclusions

The relatively fast reaction of isopropenyl chloroformate (1) versus its alkyl analog 2 in all solvents except the aqueous fluoroalchols, shows that the alkenoxy substituent exerts a powerful inductive influence on the electron density at the carbonyl atom. Unlike the solvolyses [9,23] of phenyl chloroformate (3), where the addition-elimination mechanism dominates over the full range of solvent composition including 97% HFIP, isopropenyl (1) and isopropyl (2) [27] chloroformates show varying behavior as the solvent is varied. Isopropenyl chloroformate (1) proceeds via a dominant addition-elimination mechanism (Scheme 4) in all solvents except in the four highly ionizing HFIP mixtures and 97 TFE, where a superimposed S_N1 contribution of 5–97% is estimated. On the other hand, in solvents of low nucleophilicity and high ionizing power, it was suggested [27] that isopropyl chloroformate (2) undergoes a fragmentation-ionization mechanism, involving loss of carbon dioxide. This study has further demonstrated that the use of similarity models for the elucidation of plausible solvolytic mechanisms can be useful for indicating the presence of superimposed reaction channels.