Table 1. Optimal model results.
| Effects | Estimate | 95% CI | t-value | P-value |
| Fixed | ||||
| Intercept | 6.607 | 6.271; 6.943 | 38.568 | <0.0001 |
| F | 0.349 | 0.017; 0.681 | 2.064 | 0.0392 |
| HP | –0.105 | –0.496; 0.285 | –0.529 | 0.5966 |
| R | 0.406 | 0.283; 0.529 | 6.469 | <0.0001 |
| SST | 0.092 | 0.055; 0.129 | 4.911 | <0.0001 |
| SF | –0.017 | –0.020; –0.014 | –10.242 | <0.0001 |
| Y | –0.011 | –0.025; 0.002 | –1.642 | 0.1008 |
| F×Y | –0.035 | –0.054; –0.017 | –3.812 | 0.0001 |
| HP × R | –0.299 | –0.471; –0.127 | –3.416 | 0.0007 |
| Random (SD) | ||||
Intercept (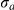 ) ) |
0.898 | 0.738; 1.091 | na | na |
Y (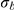 ) ) |
0.022 | 0.013; 0.039 | na | na |
Residual ( ) ) |
0.737 | 0.680; 0.800 | na | na |
| Correlation structure | ||||
align="left" valign="top">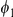
|
0.717 | 0.581; 0.814 | na | na |
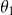
|
–0.299 | –0.412; –0.177 | na | na |
| Variance function | ||||
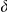
|
–0.036 | –0.057; –0.014 | na | na |
CI: confidence interval; SD: standard deviation; na: not applicable.
Parameter estimates and statistical significance from the optimal mixed-effects model with River as random grouping factor (60 levels). Abbreviations and units are described in the text and Table S3. Note that when dichotomous variables are involved the baseline case for comparison is the absence of farms and hydropower stations.
