Bistability of Cell Adhesion in Shear Flow

Abstract

Cell adhesion plays a central role in multicellular organisms helping to maintain their integrity and homeostasis. This complex process involves many different types of adhesion proteins, and synergetic behavior of these proteins during cell adhesion is frequently observed in experiments. A well-known example is the cooperation of rolling and stationary adhesion proteins during the leukocytes extravasation. Despite the fact that such cooperation is vital for proper functioning of the immune system, its origin is not fully understood. In this study we constructed a simple analytic model of the interaction between a leukocyte and the blood vessel wall in shear flow. The model predicts existence of cell adhesion bistability, which results from a tug-of-war between two kinetic processes taking place in the cell-wall contact area—bond formation and rupture. Based on the model results, we suggest an interpretation of several cytoadhesion experiments and propose a simple explanation of the existing synergy between rolling and stationary adhesion proteins, which is vital for effective cell adherence to the blood vessel walls in living organisms.

Introduction

One of the most prominent and well-studied processes of the adhesive interaction between cells is the leukocytes extravasation out of the circulatory system toward a site of tissue damage/inflammation. During this process leukocytes go through several major stages, two of which are known as rolling adhesion and stationary adhesion (1). At each of these two stages different groups of adhesion proteins play a dominant role. Selectins and their ligands provide initial bond formation (rolling adhesion) between a leukocyte and endothelium cells forming the blood vessel wall. This interaction slowdowns the leukocyte velocity and allows it to roll on the surface of blood vessels in search of a damaged/inflamed site. As soon as the rolling cell finds the damaged site, it activates another type of adhesion protein, the integrins, which cause a complete stop of the leukocyte (stationary/firm/tight adhesion).

From in vitro experiments (2) it is known that slow rolling of the cell mediated by selectins is necessary for the formation of strong integrin bonds, which cannot efficiently form at high velocities. This cooperation between the two groups of adhesion proteins is vital for the in vivo leukocytes extravasation (1). Moreover, very similar multistep adhesion is frequently observed in other cells: for example, during platelets aggregation leading to the formation of a blood clot (3). It is even used by some infectious disease agents like malaria plasmodium, which expresses adhesion proteins on the surface of an infected red blood cell causing it to stick to the blood vessel walls. This mechanism helps infected red blood cells avoid the sequestration by the spleen (4,5).

Despite the fact that cooperation between selectins and integrins is very important for an effective immune response (6–9), its mechanism is still poorly understood. So far, most of the theoretical works with a very few exceptions (10) were devoted to the rolling adhesion (11–14) only. In a recent article (10) the authors proposed one of the possible explanations of the adhesion proteins cooperativity. This study suggests that the strength of the cell adhesion rises as the number of formed bonds between the cell and the wall increases.

Existence of the two consecutive adhesion stages (rolling and stationary) in this work is explained by the different number of adhesion proteins involved in the cell adhesion—during rolling adhesion only selectins can form bonds between the cell and the wall, whereas during stationary adhesion both selectins and integrins contribute to the cell adhesion. However, if this explanation is correct and the only difference between the two stages is in the number of adhesion proteins involved in the bond formation, leukocytes can use a single type of adhesion proteins to achieve this. The proposed mechanism of the adhesion proteins' synergy provides a possible explanation, and future theoretical studies are needed to give a satisfactory answer to these questions: Why is the synergy between selectins and integrins observed in experiments so important for adhesion of cells, and what is its physical origin?

In this study we present a simple analytic model of the interaction between a leukocyte and the blood vessel wall in shear flow, which predicts that cell adhesion is a bistable process. Moreover, the model shows how physicochemical properties of adhesion proteins influence the cell adhesion bistability, and provides an explanation of the synergy between rolling and stationary adhesion proteins.

Mathematical Model

Model assumptions

When a cell forms a contact with the blood vessel wall, it starts to roll on the wall surface under the load F and torque M created by the blood flow, which is characterized by the shear rate S (see Fig. 1). During the cell rolling, new bonds between the cell and the blood vessel wall continuously form in the contact area. At the same time, previously formed bonds rupture at the trailing edge of the contact area due to the tension created by the load F and torque M.

Figure 1.

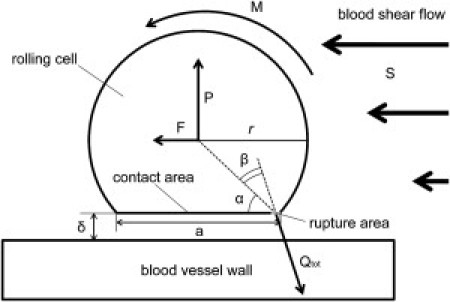
A cell rolling on the blood vessel wall in shear flow. Forces acting on the cell and the geometric parameters are shown.

In the general case, the contact area between a cell and the blood vessel wall can have a complex shape. For the sake of simplicity, this area is represented by a rectangle a × b in our model (see Fig. 2). This assumption greatly simplifies further mathematical derivations without loss of generality: Because in previous studies (11,14,15) it was shown that approximation of the contact area by a simple geometrical figure (for example, a circle) does not introduce considerable error in the final results, one can still obtain a good theoretical fitting of experimental data. Furthermore, it is known from previous theoretical works (16) that, in general, the size of the contact area may increase with the flow shear rate due to cell deformability. The change in the contact area stabilizes the cell movement making it smoother and slower. However, as suggested in Bhatia et al. (10), the cell adhesion is primarily determined by physicochemical properties of adhesion proteins and, thus, to a first approximation, the shape of the contact area can be assumed independent from the shear rate.

Figure 2.

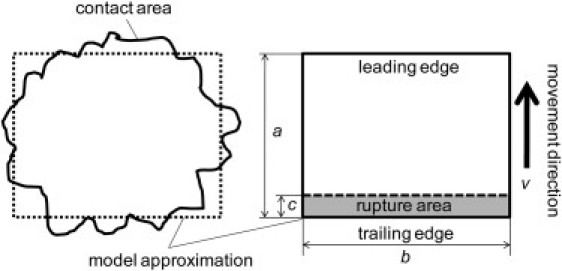
Contact and rupture area representation.

At the trailing edge of the contact area previously formed, bonds rupture under the tension created by the blood flow. The size of this rupture area, area c (Fig. 2), is determined mainly by the cytoskeleton network underlying the cell membrane. The stiffer this network, the bigger the rupture area—because more adhesion bonds share the tension (17,18).

To understand how physicochemical properties of adhesion proteins influence the cell adhesiveness, we consider in the model the simplest case when there is a single type of adhesion bonds between the cell and the wall. In the general case, each of these cell-wall bonds can be formed by two (pair) or more (cluster) of adhesion proteins. The word “bond” usually is used to address a single interaction between a pair of proteins. Thus, to avoid possible confusion, we will call cell-wall bonds in the contact area the “adhesion sites”. Each adhesion site consists of two interacting protein clusters (one on each surface), if the adhesion proteins tend to form clusters.

The average velocity of the cell and bonds tension in the rupture area

To describe the cell motion in our model, we use a steady-state approximation; we consider the long time average of the cell movement, which is typically studied in experiments. In this case the cell velocity is mainly determined by the bond rupture rate. By knowing the size of the rupture area c and the average lifetime τ of a single adhesion site in this area, it is easy to find the average cell velocity v of the cell:

$$v=\frac{c}{\tau }.$$ (1)

The average lifetime of an adhesion site in the rupture area is a function of the tension Q applied to it. This tension is related to the total tension Q_tot experienced by the all adhesion sites in the rupture area through the equation

$$KQ=Q_{tot}.$$ (2)

Here K is the total number of adhesion sites in the rupture area. Obviously, K = σbc, where σ is the surface density of adhesion sites at the trailing edge of the contact area. Thus, Eq. 2 can be rewritten as

$$Q=\frac{Q_{tot}}{\sigma bc}.$$ (3)

The total tension Q_tot is a function of the shear rate S. In the simplest case when the cell has approximately the shape of a sphere, this function may be written in an explicit form. Expressing the total tension Q_tot through the load F and torque M by solving mechanical equilibrium equations is similar to those found in Hammer and Lauffenberger (11):

$$\{\begin{array}{c}M=r{Q}_{tot}\text{sin}\beta \\ F=Q_{tot}\text{cos}\left(\alpha +\beta \right)\\ P=Q_{tot}\text{sin}\left(\alpha +\beta \right)\end{array}.$$ (4)

By using analytical expressions (19,20) for the force F and torque M acting on a rolling sphere, it is easy to show that

$$Q_{tot}\approx 4\pi \eta \frac{r^2}{a}\left[7.1rS+\left(2.4\text{ln}\left(\frac{\delta }{r}\right)-6.0\right)v\right].$$ (5)

(see the Supporting Material for more details). Here P is the normal reaction force acting on the rolling cell, which is created by compressed bonds inside the contact area (excluding the rupture area); α and β are the angles shown on Fig. 1; r is the radius of the cell; δ is the size of the gap between the rolling cell and the wall (δ << r); and η is the blood viscosity.

Concentration of adhesion sites in the rupture area

The concentration of adhesion sites in the rupture area σ can be easily estimated by considering a simple reaction A+B → AB describing the binding between adhesion proteins/protein clusters A on the cell surface and B on the blood vessel wall. The rate equations for this reaction have the form

$$\{\begin{array}{c}\frac{d{\sigma }_A}{dt}=\frac{d{\sigma }_B}{dt}=-k_{+}{\sigma }_A{\sigma }_B\\ \frac{d{\sigma }_{AB}}{dt}=k_{+}{\sigma }_A{\sigma }_B\end{array},$$ (6)

and with additional constraints,

$$\{\begin{array}{c}{\sigma }_A+{\sigma }_{AB}={\sigma }_A^0\\ {\sigma }_B+{\sigma }_{AB}={\sigma }_B^0\end{array}.$$ (7)

Here σ_A, σ_B, and σ_AB are the surface concentrations of the adhesion proteins/protein clusters A, B and adhesion sites AB at time t, respectively; σ⁰_A and σ⁰_B are the total surface concentrations of the adhesion proteins/protein clusters A and B at the leading edge of the contact area, respectively; and k₊ is the second-order reaction rate for diffusive binding of the proteins/protein clusters. Here we assume that each adhesion site has a very small probability to dissociate until it reaches the rupture area where this process is greatly accelerated. This is a reasonable assumption, taking into account that every bond in the contact area excluding the rupture area is compressed due to the blood flow pushing the cell against the wall (see Fig. 1). The bond compression reduces the dissociation rate for the reverse reaction AB → A+B, which, therefore, can be neglected. Also it should be noted that in our model we use the small Peclet number approximation (Pe << 1) (15,21), which means that the binding rate k₊ is mostly determined by the diffusion coefficient of the adhesion proteins, and is independent of the cell velocity. This approximation is based on previous theoretical studies (13), which showed that the average angular velocity of the cell Ω ≈ v/r during steady-state rolling and, thus, the relative velocity between the cell surface and the wall ≈ 0, i.e., Pe << 1.

In living cells, the rupture area is much smaller than the contact area (i.e., c << a, see Table 1). Thus, the surface concentration of the adhesion sites σ is approximately the same at any location inside the rupture area because each adhesion protein/protein cluster spends the same amount of time Δt = a/v to move from the leading edge to the trailing edge of the contact area due to its rectangular shape. Therefore, σ can be found as σ = σ_AB(Δt). Next, we consider two special cases of receptor density.

Table 1.

Values of the model parameters

Parameter	Value in the model	Typical range	References
a, Length of the contact area.	3 μm	1–4 μm	(48)
b, Width of the contact area.	3 μm	1–4 μm	(48)
c, Length of the rupture area.	100 nm	40–300 nm	(17,18,49)
r, Cell radius.	4 μm	3–4 μm	(2)
δ, Size of the gap between the cell and the blood vessel wall.	50 nm	30–60 nm (Length of adhesion proteins)	(50)
x#, Binding potential width.	0.2 nm	0.13–1.2 nm	Table S1
σtot, Total adhesion proteins density on the cell surface.	300 μm–2	50–400 μm–2	(2,22)
η, Blood viscosity.	0.002 Pa × s	0.002 Pa × s	(2)
k+, Rate for the proteins/proteins cluster binding.	0.01 μm2/s	0.006–0.6 μm2/s (Theoretical estimations)	(13,14)
koff, Unstressed bonds dissociation rate.	5 s–1	0.000005–9 s–1	Table S1
kon, Rate for a single bond formation between two proteins inside an adhesion site.	500 s–1	1–1000 s–1	Theoretical estimations
T, Temperature.	300 K

First, because, for living cells, in many cases, we have σ⁰_A ≈ σ⁰_B = σ₀ (2,22), one can find from Eqs. 6 and 7 that

$$\sigma =\frac{k_{+}a{\sigma }_0^2}{v+k_{+}a{\sigma }_0}.$$ (8)

Second, in some experiments the total surface concentrations σ⁰_A and σ⁰_B have different magnitudes (σ⁰_A << σ⁰_B or σ⁰_B << σ⁰_A) (see, for example, Brunk and Hammer (23)). In this case it is easy to acquire another useful approximation for σ, as

$$\sigma =\text{min}\left({\sigma }_A^0;{\sigma }_B^0\right)·\left[1-e^{-k_{+}a·\max \frac{\left({\sigma }_A^0;{\sigma }_B^0\right)}{v}}\right].$$ (8′)

Substituting Eq. 8 into Eq. 3, one finds that

$$Q=\frac{\left(v+k_{+}a{\sigma }_0\right)Q_{tot}}{k_{+}abc{\sigma }_0^2}.$$ (9)

The average lifetime of adhesion sites in the rupture area

To find out how the average lifetime of an adhesion site τ changes with the applied tension Q, we adopted a simple kinetic scheme depicted on Fig. 3. As in Seifert (24) and Erdmann and Schwarz (25), we assume that each protein cluster (on the rolling cell and endothelium cell) forming the adhesion site consists of N identical adhesion proteins (see Fig. S1 in the Supporting Material). Under the tension Q acting on the adhesion site, the bonds composing it start to rupture one by one until all of them are broken. Therefore, each physical state of the adhesion site can be represented by the number of bonds—from 0 to N as shown on Fig. 3. Transitions between these states can be described by rates k_i,i+1 and k_i,i−1 (0 ≤ i–1, i, i+1 ≤ N) of a single bond formation and rupture, respectively. Transition 0→1 in the general case can be neglected because after the rupture of the final bond (transition 1→0) two adhesion proteins/protein clusters which formed the adhesion site quickly become separated by a large distance. Bond formation rates k_i,i+1 are assumed to be independent from the tension as in Erdmann and Schwarz (25), while for the bond dissociation rates k_i,i−1 we use the Bell-Evans' model (26,27):

$$\{\begin{array}{c}{k}_{i,i-1}=i{k}_{off}{e}^{\frac{Q{x}^{\text{\#}}}{i{k}_{\text{B}}T}}\\ k_{i,i+1}={\left(N-i\right)}^2{k}_{on}\end{array}.$$ (10)

Here x^# is the distance between the binding potential minimum and maximum; k_on is the rate of a single bond formation between two proteins in the adhesion site (if N > 1); k_off is the unstressed rate of a single bond dissociation; k_B is Boltzmann constant; and T is temperature. In Eq. 10 we assume that the tension Q in each state i is equally distributed between the i bonds. We also take into account the fact that if there are (N–i) unbound proteins in each cluster in the adhesion site, then the total number of possible ways to form a new bond is (N–i)². The latter assumption is the only difference from the previous study (25).

Figure 3.

Kinetic scheme of the bond rupture between two protein clusters.

By using the formula of the mean turnover time for chain reactions from Bar-Haim and Klafter (28) and Cao and Silbey (29) and by assuming that during the bonds-rupture each adhesion site is in quasiequilibrium, one can find from Eq. 10 (see the Supporting Material) that the average lifetime τ of an adhesion site under the load Q is

$$\tau \left(N\right)=\frac{1}{k_{off}}\frac{\left(N-1\right)!}{N}{\left(\frac{k_{on}}{k_{off}}\right)}^{N-1}{e}^{-Q{x}^{\text{\#}}\sum _{i=1}^N\frac{i^{-1}}{k_{\text{B}}T}}.$$ (11)

Equation 11 is obtained for the case of slip bonds, i.e., for bonds which shorten their lifetimes in response to load. Some adhesion bonds may also prolong their lifetimes in response to load (catch bonds), but such a behavior takes place only at low shear rates (<100 s^–1) in experiments (30–32). These shear rates are smaller than physiological shear rates in most blood vessels (100–1000 s^–1 in venules (2,33)). Thus, at physiological conditions all adhesion bonds behave as slip bonds. As suggested in McEver and Zhu (34), it is likely that the main function of catch bonds is the prevention of inappropriate leukocytes/platelets aggregation in flowing blood rather than by the enhancement of the cell-wall interaction. Hence, the slip bond approximation is a reasonable assumption. Equation 11 is exact for N = 1,

$$\tau \left(1\right)=\frac{1}{k_{off}}{e}^{\frac{-Q{x}^{\text{\#}}}{k_{\text{B}}T}},$$ (11′)

and provides a good approximation for N > 1 for loads

$$Q<\frac{k_{\text{B}}T}{x^{\text{\#}}}\times \mathit{ln}\left[\frac{k_{on}{\left(N-\mathit{1}\right)}^2}{k_{off}}\right].$$

It must be noted, however, that the above approximation of quasiequilibrium rupture of adhesion sites gives a reasonable qualitative prediction of the relation between the cell velocity v and the shear rate of the flow S (Eq. 12) even for higher tensions.

Final equation

From Eqs. 1, 5, 9, and 11 one can get the final formula describing the relation between the cell velocity v and the shear rate S for a cell having adhesion bonds with the wall:

$$S=\frac{1}{7.1r}\left[\frac{abc{\sigma }_0{k}_{\text{B}}T}{4\pi \eta r^2{x}^{\text{\#}}(1+v/k_{+}a{\sigma }_0)\sum _{i=1}^N{i}^{-1}}·\text{ln}\left[\frac{v}{c{k}_{off}}\frac{\left(N-1\right)!}{N}{\left(\frac{k_{on}}{k_{off}}\right)}^{N-1}\right]+\left[6.0-2.4\text{ln}\left(\frac{\delta }{r}\right)\right]·v\right].$$ (12)

For a freely rolling cell, which does not have bonds with the wall, from Goldman et al. (19,20) it is easy to find that

$$S\approx \frac{v}{r}\frac{0.6-0.2\text{ln}\left(\frac{\delta }{r}\right)}{0.7}.$$ (13)

Results

Values for the all model parameters used in calculations are shown in Table 1. Bond rupture parameters x^# and k_off correspond approximately to those measured in atomic-force microscopy/biomembrane force probe (AFM/BFP) experiments for selectins (see Table S1 and Section S2 in the Supporting Material). All results presented below were obtained from Eqs. 12 and 13 by substituting the model parameters into these equations.

Bistable behavior of rolling cells

Using Eq. 12, one can easily find that the shear rate-velocity curve S(v) has a toggle-switch-like behavior (35), which is typical for bistable systems (see Fig. 4 A). When the shear rate is small, each value of S corresponds to a single value of v—identical cells have the same stationary velocity in the interval 0.5–1 μm/s (see Fig. 4, A and B; curve N = 1). The cells behavior drastically changes when S reaches ∼170 s^–1. In the interval from ∼170 s^–1 to ∼480 s^–1 there are three possible stationary velocities for each value of S. This means that there coexist three different populations of rolling cells despite the fact that all cells in the model have absolutely the same characteristics.

Figure 4.

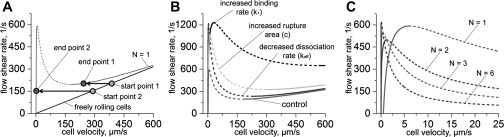
Adhesion bistability. (Solid and dashed lines) Stable and unstable solutions, respectively. (A) Bistable curve for the case of nonclustering proteins (N = 1, gray curve) and for freely rolling cells (black line) are shown. The curve minimum determines the catching effectiveness of adhesion proteins while the maximum determines the largest shear rate that adhesion bonds can withstand. (B) Influence of the model parameters on the velocity-shear rate curve shape. (Control curve is the same as the gray curve on panel A.) For the decreased-dissociation curve, the bond dissociation rate was taken to be 10 times smaller than in Table 1, i.e., k_off = 0.5 s^–1. For the increased-binding curve the bonds formation rate was taken to be 10 times bigger than in Table 1, i.e., k₊ = 0.1 μm²/s. For the increased-rupture-area curve, the rupture area size is c = 350 nm. (C) Influence of proteins clustering on the velocity-shear rate curve. Curves for different numbers (N) of proteins in adhesion sites are shown. Values of the model parameters used in calculations for panels A and C are shown in Table 1.

The slowest population has approximately the same velocity as for S < 170 s^–1 (v ∼1–3 μm/s), whereas the fastest one has velocity which is almost the same as the velocity of freely rolling cells (which do not have any bond with the wall). Using simple arguments (see the Supporting Material), it is easy to show that only the high and low velocity branches are stable while the medium branch is unstable (see Fig. 4 A). This unstable part of S(v) curve corresponds to the boundary between the attraction domains of the left and right stable branches. If a cell starts from the point slightly to the left of the unstable branch, it will reduce its speed and finally reach the left stable branch; otherwise, if it starts slightly to the right, it will accelerate to the higher velocity corresponding to the right stable branch.

Further increase of the shear rate S leads to the disappearance of the left stable and unstable branches. In other words, a critical value of the shear rate (the curve maximum) exists beyond which cells cannot form a strong attachment with the blood vessel wall. Such a critical shear rate is indeed observed in experiments (12,23). The maximum of the shear rate-velocity curve corresponds to the velocity at which adhesion proteins work at full capacity (the dynamic strength of which comes from their ability to form bonds and resist tension).

The “catching” effectiveness of adhesion proteins

Maximum and minimum of the S(v) curve on Fig. 4 A corresponds to two important parameters describing the effectiveness of cell adhesion. As mentioned above, the maximum represents the highest shear rate, which adhesion bonds can withstand, whereas the minimum represents the “catching” effectiveness of adhesion proteins. Cells moving in the blood flow slow down to rolling velocities corresponding to the left stable branch only at shear rates smaller than the shear rate at the curve minimum. Otherwise, cells gather on the right stable branch, which corresponds to rapidly moving cells. This behavior can be inferred from the following procedure.

Let us choose any point on the line corresponding to freely rolling cells (see Fig. 4 A). Assuming that the shear rate is constant in the blood vessel and plotting a horizontal line starting from this initial point, one must check which stable branch is intersected initially by the horizontal line. This intersection point corresponds to the final steady-state velocity of the cell. Thus, it is easy to verify that the S coordinate of the curve minimum determines the shear-rates interval in which cells can slow down to low rolling velocities (i.e., the left stable branch). In a real system, due to the fluctuations in cell velocities (23,36–38), this catching-feature of adhesion proteins is smeared because the fluctuations allow cells to jump from one stable branch to another at shear rates above the minimum. Nevertheless, position of the curve minimum is still a good indicator of the adhesion proteins' catching effectiveness.

Using our analytic model we tested how changes in different model parameters influence the maximum detachment force and the catching-effectiveness described above. Calculations showed that the curve maximum rises when (see Fig. 4 B):

• 1.The proteins' mobility (binding rate k₊) increases, because this leads to a larger number of bonds between the cell and the wall;
• 2.The rupture area size (c) increases, because this leads to a larger number of bonds resisting the flow pushing force; and
• 3.The bond dissociation rate (k_off) decreases, which means the bonds become stronger.

At the same time, the catching-effectiveness can be improved only by increasing the mobility of the proteins (k₊), whereas changes in the rupture area size (c) and the bond dissociation rate (k_off) have only a minor influence on it. This difference between the maximum and minimum of the S(v) curve has a simple interpretation. For the bond rupture process, which determines the curve maximum position, both the number of bonds resisting the load (depends on c and k₊) and their strength (depends on k_off) are important. In contrast, the curve minimum position, which is indicator of the adhesion proteins' catching-effectiveness, is related to the bond formation process. This is why it is mostly determined by the rate of proteins binding (k₊).

Clustering versus nonclustering adhesion proteins

Another interesting finding of this work is the synergetic behavior of adhesion proteins in interacting clusters during cell adhesion. By using Eq. 12, it is easy to find that the shear rate-velocity curve S(v) shifts to smaller velocities as the number of proteins in adhesion sites N increases (see Fig. 4 C). This curve behavior results from the cooperation between the clustered proteins. Consider, as a first case, an adhesion site consisting of a single pair of interacting proteins (N = 1, nonclustering proteins). These proteins quickly become separated after the bond between them ruptures. Thus, chances that they will form the bond again are negligible. Now consider a second case, that of an adhesion site formed by two clusters of proteins (N > 1, clustering proteins). Here, the situation is different. When one of the bonds inside the adhesion site ruptures, the unbound proteins do not move apart (as long as this is not the final bond). Therefore, the unbound proteins can rapidly restore the ruptured bond, because they do not need to diffuse over a long distance in a search of a binding partner. As a result, an adhesion site formed by two protein clusters is more resistant to the tension created by the blood flow than in the case of nonclustering adhesion proteins. Thus, a higher shear rate is needed to force the cell movement with the same velocity in the case of clustering receptors (i.e., the front of the S(v) curve shifts to smaller velocities).

Consistency with previous experimental findings

To verify whether our model correctly fits experimental data, we fitted experimental results from Brunk and Hammer (23) using our model. In this work, Brunk and Hammer used a cell free assay to characterize a single bond type (E-selectin and its ligand). The cell free assay helps to avoid multicomponent interactions, which are known to exist in living cells, because many adhesion receptors impart a primary ligand that can interact with other adhesion molecules (34,39). These secondary interactions can modulate the cell adhesion strength and a more complex mathematical model taking into account these multicomponent interactions is needed to describe behavior of living cells.

We found that theoretical fitting based on our model and existing AFM/BFP measurements of the bond rupture parameters agrees very well with experimental data from Brunk and Hammer (23) (see Fig. 5). Moreover, our model predicts that the slow rolling of microspheres cannot be observed at shear rates >220 s^–1 (the shear rate at the maximum). This finding is in a good agreement with the experimental observations. Similar behavior of microspheres was also found in Yago et al. (40) and Rodgers et al. (41).

Figure 5.

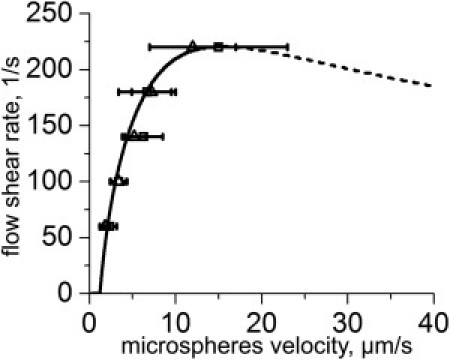
Microsphere rolling adhesion. Experimental data from Brunk and Hammer (23) was fitted with modified Eq. 12. For theoretical curve, we used Eq. 8′ instead of Eq. 8. The model parameter values, i.e., r = 5 μm, σ⁰₁ = 90 μm^–2, σ⁰₂ = 3600 μm^–2, and η = 0.001 Pa × s (water), were taken from Brunk and Hammer (23). The size of the contact area (a = b = 1.3 μm) was estimated from the microsphere (r = 5 μm) and bond (δ = 50 nm) geometry. The bond rupture parameters x^# = 0.12 nm and k_off = 5 s^–1 were taken from AFM/BFP experiments (see Table S1 in the Supporting Material). The rupture area size c and the binding rate k₊ were varied to achieve the best data-fitting (c = 200 nm and k₊ = 0.006 μm²/s).

Another prediction of our model which can be verified experimentally is existence of adhesion hysteresis. As mentioned above, cells/microspheres slow down and form multiple bonds with the wall only if the flow shear rate is smaller than the shear at the S(v) curve minimum. However, to detach cells/microspheres from the wall, the higher shear rate corresponding to the S(v) curve maximum is needed. Hence, the detachment shear rate is larger than the attachment shear rate. This means that there is a hysteresis loop, which results from the bistability in cell adhesion. Indeed, some existing experimental results support this model prediction. In Lawrence and Springer (2), the authors found that, to initiate integrin bond formation, the shear rate must be dropped to very small values (∼36 s^–1). At the same time, the detachment shear rate for the same bonds was >3600 s^–1. I.e., there was a huge adhesion hysteresis loop in the experimental system. In contrast to integrins, selectins in the same experiments had much higher capturing effectiveness, but they were not able to stop cells movement completely.

Discussion

Model predictions

By using a simple analytic model, we showed that the process of cell adhesion to the blood vessel wall in shear flow has a bistable behavior. This bistability results from the competition between two kinetic processes.

The first process is the bond formation between the rolling cell and the blood vessel wall. This process inversely depends on the rolling velocity—the higher the velocity, the fewer the number of bonds formed between the cell and the wall because each adhesion protein has a shorter time to find a binding partner. Therefore, the lower shear rate is needed to keep the cell rolling.

The second process is the bond dissociation in the rupture area. The rate of the bond rupture (and, hence, the rolling velocity) increases with the flow shear rate. Thus, the shear rate and the rolling velocity are anticorrelated in these two processes, which compete with each other. Because both kinetic processes are in action during cell adhesion, the adhesion bistability is an intrinsic property of a rolling cell. This adhesion bistability can be found in a very wide range of the model parameters that characterize the geometrical and physicochemical properties of adhesion proteins and the cell.

Due to the adhesion bistability, the shear rate-velocity curve S(v) has two bifurcational points corresponding to the curve maximum and minimum. These two points determine the effectiveness of cell adhesion. The maximum corresponds to the highest shear rate the bonds between the cell and the wall can withstand, whereas the minimum characterizes the catching efficiency of the bonds (an upper shear rate limit above which cells attach to the blood vessel wall). Physicochemical properties of adhesion proteins determine positions of both extremum.

To perform their major functions, rolling adhesion proteins must have a high catching effectiveness and, at the same time, allow the rolling movement of cells. The high catching rate allows the effective recruitment of cells from the blood stream to the blood vessel wall, whereas the rolling movement is needed for the cells' mobility during their search for an inflamed/damaged site. Our model shows that the catching effectiveness is mostly determined by the protein binding rate (k₊). The higher the binding rate and receptors' mobility, the larger their catching effectiveness. At the same time, the bonds dissociation rate k_off must be high enough to allow for rolling of the cell. Otherwise, the left stable solution branch of the S(v) curve shifts to vanishingly small velocities (Fig. 4 B), meaning that the wall bounded cells do not move if k_off is small. These two results agree well with experimental data (34)—it is well known that rolling adhesion proteins (selectins) possess both of these properties (high binding and rupture rates).

After a leukocyte/platelet finds an inflamed/damaged site, it activates stationary adhesion proteins, which cause a complete stop of the cell. Thus, stationary adhesion proteins must be able to form strong bonds, which can withstand the blood-flow pushing force. For this purpose, the maximum of S(v) curve must be very high and the left stable branch must approach zero velocity as closely as possible. Then it follows that stationary adhesion proteins must have very small dissociation rate (k_off) (see Fig. 4 B). Evidently, this requirement for the stationary adhesion proteins is opposite to the above requirement for the rolling adhesion proteins (large k_off). Therefore, these two stages of cell adhesion must be mediated by physically different proteins (although this can be the same type of protein but in two different physicochemical conformations).

Moreover, as we found in this study, the protein clustering also may help to shift the S(v) left stable branch to smaller velocities (making cell adhesion stronger; see Fig. 4 C). Experiments show that after activation both of these changes take place in integrins: they switch from the low to the high affinity state (k_off decreases) (42,43) and start to aggregate in clusters. The clusters can be formed either by direct integrin-integrin interaction (44) or through interactions with other accessory proteins (45); for example, talin, which connects integrins to the cellular cytoskeleton. In the latter case, the cytoskeleton helps to redistribute the total bonds tension Q_tot between more of the adhesion proteins, thus increasing the effective rupture area size and decreasing the individual tension of each bond Q. This, in turn, results in the increase of the maximum of the S(v) curve according to our model (see Fig. 4 B). Thus, integrins-cytoskeleton interaction provides a large contribution to the strength of cell adhesion. Other mechanisms like recruitment of adhesion proteins into lipid rafts (43) or into areas of membrane curvature (46) may also be involved in the formation of protein clusters.

In general, protein clusters have a lower mobility than single proteins due to a larger size. In addition, receptors-clustering results in a smaller concentration of diffusing complexes on the cell surface. Existing experiments also suggest that interaction of adhesion proteins with the cytoskeleton even further reduces their diffusion coefficient (47). According to our model, all these three mechanisms lead to a large decrease in the catching effectiveness of stationary adhesion proteins. This result agrees very well with experimental data (2,3). Therefore, for efficient cell adhesion to the blood vessel walls, both types of adhesion proteins (stationary and rolling), which specialize in two different functions (cell catching and stopping), are needed (see Fig. 6). Indeed, signs of such synergy between the two types of proteins were found in many different types of cells (2–5).

Figure 6.

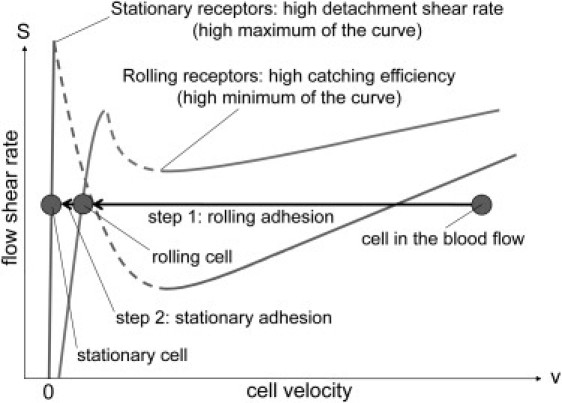
Synergy between rolling and stationary adhesion proteins. Rolling adhesion receptors mediate initial bond formation between a cell and the blood vessel wall and provide the slow rolling of the cell. Stationary adhesion receptors are needed for a strong cell attachment to the wall, which can withstand a large pushing force created by the blood flow.

Experimental verification of the model predictions

What is the simplest way to measure the adhesion proteins' catching effectiveness and the maximum strength in experiments, and to test the model predictions about the adhesion bistability and protein's synergy?

One can try to measure in experiments the flow shear rate-cell velocity curve. By doing this, it is possible to obtain the position of the curve maximum. Unfortunately, the position of the curve minimum can hardly be determined in such an experiment, because it is very difficult to distinguish, in experiments, freely rolling cells and cells corresponding to the right stable branch of the curve because they have very similar velocities (see Fig. 4 A). To measure the positions of the curve extremum, one can instead use a general property of bistable systems—i.e., existence of a hysteresis loop (see Fig. 7 A).

Figure 7.

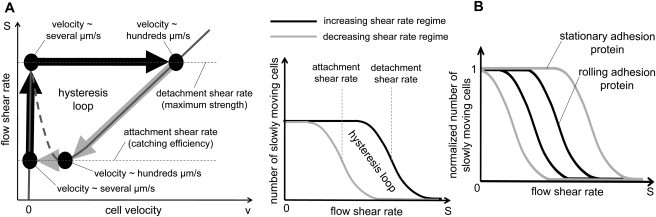
Adhesion hysteresis. (A) (Left panel) Existence of a hysteresis loop is a general property of a bistable system. As the flow shear rate increases from a small value, cells, initially attached to the wall, detach at the shear rate corresponding to the S(v) curve maximum. If the shear rate decreases, the process is reversed; cells reattach to the wall, but at the smaller shear rate corresponding to the S(v) curve minimum. The difference between the shear rates of the curve maximum and minimum is the main cause of the adhesion hysteresis. (Right panel) Schematic explanation of the main idea of experiment, which can verify existence of cell adhesion bistability. Upon counting the number of cells attached to the flow chamber surface as a function of the flow shear rate during the two working regimes (increasing and decreasing shear rate), one will observe the gap between the two curves, if cell adhesion process has a bistable behavior. The two middle points of the resultant curves correspond to the catching effectiveness (left curve) and the maximum strength (right curve) of adhesion proteins. (B) If the model prediction about the origin of synergy between the rolling and stationary adhesion proteins (Fig. 6) is correct, the hysteresis loop of the rolling adhesion proteins must be contained inside the hysteresis loop of the stationary adhesion proteins.

In a specifically designed flow chamber with the coverslip coated by adhesion proteins one can measure the number of  cells attached to the coverslip as a function of flow shear rate. Upon increasing the shear rate in the chamber from a small to high value, one will observe that cells start to detach from the coverslip at some shear rate, which approximately corresponds to the shear rate at the curve maximum (detachment shear rate) according to our model (see Fig. 7 A, left panel). Thus, there will be a drop in the number of cells attached to the coverslip at this point (see Fig. 7 A, right panel). If the shear rate after that is decreased from a high to a low value, cells will start to reattach to the coverslip, but at a smaller shear rate corresponding to the curve minimum (attachment shear rate), if the model prediction about the cell adhesion bistability is correct.

Hence, if cell adhesion process has a bistable behavior there will be a gap between the two curves (hysteresis loop; see Fig. 7 A, right panel). Such an experiment allows us to verify the model prediction about the bistability of cell adhesion and to measure the maximum strength (see middle of the right slope, Fig. 7 A, right panel) and catching efficiency (see middle of the left slope, Fig. 7 A, right panel) of adhesion proteins.

Furthermore, the same experiment can be used to test the model prediction about the synergy between rolling and stationary adhesion proteins. As mentioned above, our model suggests that rolling adhesion proteins must have higher catching efficiency than stationary adhesion proteins, but the latter must have higher maximum strength than the former. Thus, if the model prediction of the synergy origin is correct, the hysteresis loop obtained for rolling adhesion proteins must be smaller than the hysteresis loop for stationary adhesion proteins at physiological concentrations of both proteins (see Fig. 7 B).

In short, it would be important to perform such experiments and to verify the model predictions about adhesion bistability, hysteresis loop, and the synergy between the two types of proteins. Indeed, our preliminary results are in good agreement with our theoretical predictions and will be reported in a separate article prepared jointly with investigating colleagues.