Abstract
In this paper, based on a recent work by McAllister and Floudas who developed a mathematical optimization model to predict the contacts in transmembrane alpha-helical proteins from a limited protein data set [1], we have enhanced this method by 1) building a more comprehensive data set for transmembrane alpha-helical proteins and this enhanced data set is then used to construct the probability sets, MIN-1N and MIN-2N, for residue contact prediction, 2) enhancing the mathematical model via modifications of several important physical constraints and 3) applying a new blind contact prediction scheme on different protein sets proposed from analyzing the contact prediction on 65 proteins from Fuchs et al. [2]. The blind contact prediction scheme has been tested on two different membrane protein sets. Firstly it is applied to five carefully selected proteins from the training set. The contact prediction of these five proteins uses probability sets built by excluding the target protein from the training set, and an average accuracy of 56% was obtained. Secondly, it is applied to six independent membrane proteins with complicated topologies, and the prediction accuracies are 73% for 2ZY9A, 21% for 3KCUA, 46% for 2W1PA, 64% for 3CN5A, 77% for 3IXZA and 83% for 3K3FA. The average prediction accuracy for the six proteins is 60.7%. The proposed approach is also compared with a support vector machine method (TMhit [3]) and it is shown that it exhibits better prediction accuracy.
1 Introduction
Protein structure prediction has experienced significant progress during the past years [4, 5, 6, 7]. Various methods, such as comparative modeling [8, 9, 10, 11], fold recognition and threading [12, 13, 14, 15], first principles prediction with database information [16, 17, 18, 19], and first principles prediction without database information [20, 21, 22, 23] contributed to this advancement. Most of these methods utilize a multi-step process, which often includes secondary structure prediction, contact prediction, fragment generation, clustering, etc.. However, the structure prediction for membrane proteins is less investigated. This is mainly due to the fact that limited experimental structures are available to researchers and the phospholipid bilayer environment has to be considered in the modeling process.
Membrane proteins constitute about 30% of all proteins. They play vital roles in all the organisms, acting like filters between the intra- and extra-cellular domains or between cells, transporting small molecules and energy [24, 25, 26]. Due to their vital functions in the cells, membrane proteins make about 50% of the current drug targets [27], thus providing high-resolution three dimensional structural information of membrane proteins is of crucial research and medical interests. However, membrane proteins are difficult to be crystallized for X-ray analysis, and less than 1% of the protein structures deposited in Protein Data Bank are membrane proteins [28]. This restricts severely the development of homology-based structure prediction method since they can not be universally applied to membrane proteins [26]. A recent study showed that, given an available template and the sequence similarity between the template and the target is greater than 30%, homology modeling of membrane proteins can generate comparable structures to water-soluble proteins [29]. Another difficulty for membrane protein structure prediction is that modeling and predicting membrane proteins have to include the effect of phospholipid bilayers, thus new energy functions must be formulated [30] or the appropriate lipid environment needs to be considered [31]. By using a low-resolution scoring function including an environment score function, Yore-Yarovoy et al. predicted significant portion of each of 12 test proteins within 4 Å RMSD value by using Rosetta de novo structure prediction method [32]. Zhang et al. incorporated explicitly a “hydrophilic inside” potential term in TASSER and used this potential to model the predicted transmembrane regions; and a final model for bovine rhodopsin predicted by TASSER achieved a RMSD of 4.6 Å [33].
Barth et al. recently developed a method to predict membrane protein structures by constraining the orientations of transmembrane helical segments and fixing residue-residue interactions either from predictions or derived from experimental information [26]. It is concluded that membrane protein structure prediction can reach 4 Å of native structure if limited information on residue-residue interactions is available. In fact, experimental techniques such as mutagenesis and cross-linking assays have long been used to study the structure-function relations in transmembrane proteins [34]. The residue contact information predicted or derived from experimental data guides the simulation to find the native three dimensional structures by narrowing down the conformational sampling space. More recently, Michino et al. developed a protocol for predicting a special class of membrane proteins in complex with a ligand, GPCRs (G protein-coupled receptors) of class A [35]. This protocol used predicted inter-residue contacts and an all-atom implicit membrane GB (Generalized Born) force field. The method generated models with 2.0 Å Cα RMSD from the crystal structure for protein βAR.
Residue-residue contact prediction can not only help membrane protein structure prediction, but can also facilitate the methods developed for structure prediction of water-soluble proteins, and help to understand protein folding and stability [36]. Many efforts have been done in studying residue-residue contact (interactions). Tanaka and Scheraga classified the residue-residue interactions into short, medium and long range ones and proposed a three-step protein folding mechanism based on these interactions [37]. By using a protein as an example, BPTI, Wako and Scheraga developed a method to evaluate the quality of the residue-residue interaction distances, and even provided an empirical relation between the ambiguity in the computed conformation and RMSD value of the computed conformation [38]. In order to facilitate the structure prediction for globular proteins, various research groups have developed different contact prediction algorithms for globular proteins [39, 40, 41, 42, 50, 51, 52, 53, 54]. They can be broadly classified into three categories: correlated mutation analysis [40, 55], machine learning methods [50, 53, 56], and mathematical optimization based methods [39, 42, 43]. Correlated mutation analysis is based on the observation that two mutations often take place in tandem. The prediction capability of correlated mutation analysis is relatively low compared with machine learning methods, such as neural network [53], and support vector machine [50, 57]. Combinations of different methods are also used for contact prediction in a hope of providing better prediction power. Examples are combination of hidden Markov model with support vector machine, or genetic programming [58]. The third category is optimization based approaches. This approach showed promising prediction ability [39, 42, 43]. In a recent work by Rajgaria et al., an optimization model was introduced to predict the hydrophobic to hydrophobic residue contacts in alpha-helical proteins with an accuracy about 66% [42]. This was extended for mixed alpha/beta proteins in another work by Rajgaria et al. by including more features and constraints in the model [43]. An average prediction accuracy of 61% was achieved and the predicted residue contacts were helpful with the protein three dimensional structure prediction by first principles protein tertiary structure prediction approach, ASTRO-FOLD [21, 23, 44, 45, 46, 47, 48, 49]. Note that even though there are false predicted contacts by these methods, the predicted contacts can still be used to help predicting the three dimensional structures for proteins. Latek and Kolinski recently showed that using their CABS force field can suppress the false predicted contacts, thus guiding the simulation to find the correct structure restrained by the true contacts [58].
Although contact prediction for globular proteins has made great advancement, contact prediction for membrane proteins is less studied. One reason is that the contact prediction models for globular proteins can not be simply used in membrane proteins. For example, the contact prediction model developed by Rajgaria et al. maximizes the sum of hydrophobic contact energies between the contact residue pairs [42, 43]. This model uses the assumption that the lowest energy structure corresponds to the native structure, and this assumption can not be directly applied to membrane proteins.
Few attempts have been made for predicting the contacts in transmembrane helical proteins. Fuchs et al. developed a neural network method for predicting the inter-helical contacts in transmembrane proteins [2]. This is claimed to be the first published contact prediction method for membrane proteins, even though McAllister and Floudas (2008) presented an optimization based approach earlier [1]. The method by Fuchs et al. incorporates membrane protein specific features such as number of transmembrane helical segments, their positions and orientations into different neural network models. The best prediction accuracy achieved by the different neural networks is about 26% given a contact defined as the minimal distance between side chain or backbone heavy atoms is less than 5 Å. This method has been compared with several other contact prediction methods designed for globular proteins, and it is concluded that the prediction methods for globular proteins are not able to predict contacts with a comparable accuracy within transmembrane helical segments [2].
A support vector machine model for residue contact prediction of membrane proteins was recently developed by Lo et al. [3], and these predicted contacts are further used by the model to predict the interacting pair of helices. A residue prediction accuracy of 44.8% was achieved on an independent test set of proteins. It is reported that when at least three residue contacts are used for inferring a helical pair interaction, the prediction accuracy for the interacting helical pairs is 56%. A similar work by Nugent and Jones also relied on support vector machine for predicting the transmembrane helix packing through the use of residue contacts and a force directed algorithm [59]. The model is claimed to predict helix-helix interaction with up to 65% accuracy when tested by cross-validation on a non-redundant set.
In December 2008, McAllister and Floudas introduced a mixed integer programming (MIP) optimization based contact prediction model for transmembrane alpha-helical proteins [1]. This model assumes that some specific residues have higher probabilities of forming an inter-helical contact than other residues. By building pairwise (PAIRWISE) and three-residue (TRIPLET) contact probability sets based on a data set of transmembrane alpha-helical proteins, the approach successfully predicted residues contact for several transmembrane alpha-helical proteins, including a seven helical bundle protein, bovine rhodopsin [1]. Two different optimization models, PAIRWISE and TRIPLET, together with four different probability sets, were used to predict the inter-helical contacts in this work. Data from a limited number of available transmembrane alpha-helical proteins (26 proteins and 42 chains) were used.
Using an enlarged set of transmembrane alpha-helical proteins in PDB, we enhance the model by building new probability sets to satisfy the demand of high quality inter-helical contact predictions in transmembrane proteins. The new probability sets in this article are based on a combined data set from three different membrane protein data banks, Membrane Protein Topology Database (MPTopo) [60], Membrane Protein Data Bank (MPDB) [61] and Protein Data Bank of Transmembrane Proteins (PDBTM) [62].
The work in this article aims to firstly improve the model by constructing the enhanced probability sets and modifications of several physical constraints. Secondly, it aims to provide a method to predict residue contacts for blind predictions. In the original work, the evaluation of the predictions for a single run was based on the best average contact distances (the smallest average contact distance of all iterations during a run is defined as the best average contact distance). Because the distance information of a protein for a blind prediction is unknown, providing a systematic procedure to predict the best inter-helical contact prediction is of significance. The models are firstly applied to 65 test proteins which are collected from the paper by Fuchs et al. [2], and later by analyzing the effect of different parameters on the prediction accuracy, we developed a protocol for transmembrane helical residue contact prediction. The protocol has been applied on two additional test sets of proteins: the first set of five proteins is selected from the training protein set used for building the probability sets. They are carefully chosen so as to represent various topologies. An independent set of six non-redundant proteins is built from proteins released after Feb. 2009 in the membrane protein data banks PDBTM and MPDB. These six proteins are all subject to a sequence similarity check (35%) by PISCES [65]. Average accuracy of 56% is obtained for the first set of five proteins and average accuracy of 60.7% is obtained for the second set of six independent proteins. A comparison with a support vector machine method, TMhit [3], shows that the proposed approach produces better results when tested on the set of six proteins.
2 Material and Methods
2.1 Enhanced Probability Sets
In the previous work by McAllister and Floudas (2008), the inter-helical contact prediction for membrane proteins was achieved by building two mixed integer programing optimization models, namely PAIRWISE and TRIPLET [1]. The models predict the residue contacts between different transmembrane helical segment by maximizing the occurrence of the most probable residue pairs. A data set consisting of 26 unique helical membrane proteins (42 chains) was compiled from MPTopo [60]. Based on this data set, the PAIRWISE and TRIPLET inter-helical contact probabilities (namely, MIN-1 and MIN2) were developed. For the probability construction, a PAIRWISE inter-helical contact is defined as if two amino acids in two different transmembrane helical segments are within 4 to 10 Å; a TRIPLET inter-helical contact is defined for three amino acids with one amino acid in a transmembrane helical segment (MAIN residue) contacting with two other amino acids (SECONDARY residues) in the corresponding contacting transmembrane helical segment, and a TRIPLET contact happens if the average distance between MAIN residue and SECONDARY residues is between 4 to 10 Å. It should be noted that there were two other probability sets, AL-P (pairwise contact probability set) derived from the work of Adamian and Liang [63], and AL-T (triplet contact probability set) derived from Adamian et al. [64].
In this paper, the AL-T and AL-P probability sets used are adopted directly from Ref. [1]. Two new probability sets (MIN-1N and MIN-2N) are build based on an enhanced transmembrane helical protein data set. The probability sets of MIN-1N and MIN-2N are listed in supplementary material from Table 1 to Table 9. This data set combines all the transmembrane alpha-helical membrane proteins in Membrane Protein Topology Database (MPTopo) [60], Membrane Protein Data Bank (MPDB) [61] and Protein Data Bank of Transmembrane Proteins (PDBTM) [62]. The alpha-helical membrane protein list of each data bank is first culled through an online server PISCES to get a non-redundant list [65]. PISCES determines sequence identities by a combination of Combinatorial Extension (CE) structural alignment and PSI-BLAST sequence alignment [65, 66]. The culling parameters used for PISCES server are: Maximum percentage identity: 35%; Skip non-X-ray entries? No; Skip CA-only entries? No; with other threshold values set as default.
Table 1.
The data set of alpha-helical membrane proteins. Listed are the PDB codes with chain ID, and the number of amino acids.
| protein | length | protein | length | protein | length | protein | length |
|---|---|---|---|---|---|---|---|
| 1A91A | 79 | 1VF5A | 215 | 2H88D | 154 | 2R6GE | 370 |
| 1AFOA | 40 | 1VF5B | 160 | 2H8AA | 578 | 2R6GF | 514 |
| 1AR1B | 298 | 1VRYA | 76 | 2HYDA | 336 | 2R6GG | 296 |
| 1C17M | 177 | 1WPGA | 994 | 2I5NC | 137 | 2R9RA | 333 |
| 1H2SA | 225 | 1XIOA | 261 | 2I68A | 182 | 2R9RB | 514 |
| 1H2SB | 60 | 1XL4A | 301 | 2IC8A | 122 | 2RH1A | 500 |
| 1JB0A | 755 | 1XMEA | 568 | 2IH3C | 359 | 2UUIA | 156 |
| 1JB0K | 83 | 1Y5IA | 1246 | 2J58A | 500 | 2VPZA | 765 |
| 1JB0L | 154 | 1Y5IB | 512 | 2J7AA | 159 | 2VPZC | 253 |
| 1KF6B | 243 | 1Y5IC | 225 | 2J7AC | 1055 | 2Z73A | 448 |
| 1KF6C | 130 | 1YCEA | 89 | 2J8SA | 169 | 2Z9AA | 88 |
| 1KF6D | 119 | 1YEWA | 382 | 2J8SD | 274 | 3B9WA | 407 |
| 1KQFA | 1015 | 1YEWB | 247 | 2JAFA | 510 | 3BZ1A | 344 |
| 1KQFC | 217 | 1YEWC | 289 | 2JIZA | 482 | 3BZ1B | 510 |
| 1L9BC | 124 | 1YGMA | 118 | 2JIZD | 272 | 3BZ1C | 473 |
| 1M0KA | 262 | 1Z98A | 281 | 2JIZG | 501 | 3BZ1D | 352 |
| 1MHSA | 920 | 2A65A | 519 | 2JLNA | 44 | 3BZ1U | 104 |
| 1NEKC | 129 | 2AKHA | 77 | 2JWAA | 93 | 3BZ1V | 137 |
| 1NEKD | 115 | 2AKHB | 400 | 2K2FA | 183 | 3BZ1Z | 62 |
| 1OKCA | 297 | 2AKHC | 111 | 2K73A | 337 | 3C02A | 258 |
| 1OTSA | 465 | 2BBHA | 269 | 2NQ2A | 253 | 3CP1A | 86 |
| 1P49A | 562 | 2BG9A | 370 | 2NQ2C | 116 | 3CX5A | 431 |
| 1PPJA | 446 | 2BHWA | 232 | 2NS1B | 422 | 3CX5B | 352 |
| 1PPJB | 439 | 2BL2A | 156 | 2NWLA | 234 | 3CX5C | 385 |
| 1QCRH | 60 | 2BS2B | 241 | 2O9GA | 114 | 3CX5D | 248 |
| 1RZHL | 281 | 2BS2C | 256 | 2Q67A | 326 | 3CX5F | 146 |
| 1RZHM | 307 | 2CFQA | 417 | 2QI9A | 249 | 3CX5G | 126 |
| 1U19A | 348 | 2CPBA | 50 | 2QI9C | 245 | 3CX5W | 108 |
| 1U7GA | 385 | 2F2BA | 246 | 2QI9F | 321 | 3D31A | 348 |
| 1V54A | 514 | 2H3OA | 61 | 2QKSA | 438 | 3D31C | 295 |
| 1V54B | 227 | 2H88A | 621 | 2QTSA | 154 | 3DDLA | 273 |
| 1V54C | 261 | 2H88B | 252 | 2QWWA | 381 | 3DH4A | 530 |
| 1V54E | 109 | 2H88C | 140 | 2R6GA | 370 | 3EAMA | 317 |
| 1V54H | 85 | ||||||
Table 9.
Prediction accuracies of six test proteins for our method and TMhit. The accuracy for TMhit(Top20) is based on the first 20 predicted residue contacts. The accuracy for TMhit(L/5) is based on L/5 predicted residue contacts. The accuracy for TMhit(L/2) is based on L/2 predicted residue contacts (where L is the total length of transmembrane segments). Numbers in parentheses indicate the number of predicted residue contacts used for evaluation.
| PDB ID | 2ZY9A | 2W1PA | 3CN5A | 3KCUA | 3IXZA | 3K3FA | ave |
|---|---|---|---|---|---|---|---|
| Proposed method | 73%(26) | 46%(24) | 64%(22) | 21%(29) | 77%(31) | 83%(24) | 60.7% |
| TMhit (Top20) | 100%(20) | 50%(20) | 30%(20) | 20%(20) | 10%(20) | 25%(20) | 39.2% |
| TMhit (L/5) | 100%(24) | 67%(15) | 43%(14) | 13%(30) | 8%(25) | 20%(44) | 41.9% |
| TMhit (L/2) | 68%(60) | 42%(36) | 34%(35) | 15%(74) | 5%(61) | 16%(108) | 29.9% |
The Membrane Protein Topology Database (MPTopo) includes membrane proteins with experimentally validated transmembrane segments, and is maintained by the Stephen White laboratory at University of California, Irvine [67]. The 3D_Helix set are helical membrane proteins with known three dimensional structures and thus are used for probability construction. After culling the highly similar sequences by PISCES [65], an inspection was performed in order to exclude the proteins with only one alpha-helical segment, or with more than one but no clear helical contacts between different the transmembrane alpha-helical segments. A final list of 26 unique proteins (42 chains) were obtained [1]. Since MPTopo has not been updated since Aug. 2007, and McAllister and Floudas downloaded the data set on Sep. 2007, the protein list used in their work are simply adopted here [67].
Protein Data Bank of Transmembrane Proteins (PDBTM) [62] is a membrane protein data bank which collects all the membrane proteins from the official Protein Data Bank by using an automated algorithm TMDET [62]. TMDET scans the newly released structures in Protein Data Bank every week and identifies the membrane proteins with a discrimination power greater than 98%. Thus, it provides a more complete and up-to-date membrane protein data set than MPTopo. PMDET also identifies the location of the lipid bilayer that is relative to the coordinate system and assigns transmembrane character for each membrane protein in Protein Data Bank. As of Feb 22, 2009, 187 non-redundant transmembrane helical proteins (255 unique chains) exist in PDBTM and this list is downloaded from PDBTM website. The downloaded list of proteins is subject to the culling server PISCES to remove the redundant or highly-similar structures. 90 unique proteins (113 unique chains) were left after the culling process.
MPDB refers to Membrane Protein Data Bank, and it is updated weekly in parallel with Protein Data Bank and maintained by Raman et al. [61]. MPDB contains not only structural but also functional information of integral, anchored and peripheral membrane proteins. The membrane protein selection procedure consists mainly of manual inspection on the PDB entries containing ’membrane’. Ambiguous data are retrieved from the source literature and related database. MPDB provides different criteria to search the transmembrane proteins. Through a customized search (http:www.mpdb.ul.ie/customseach.asp), a total of 530 alpha-helical transmembrane proteins are downloaded. This list is again culled against PISCES so that the highly similar ones are eliminated. A total of 75 unique proteins (152 unique chains) is obtained. The options used for downloading the transmembrane alpha-helical proteins from MPDB are: Membrane disposition: Transmembrane (Polytopic: crosses the membrane more than once); Secondary structure of transmembrane domain: alpha-helical; Number of membrane crossings: Minimum=2 and Maximum=50 (default); Publication year high: 2009; with other threshold values set as default.
At a later stage, the three separately obtained data sets of MPDB, PDBTM and MPTopo are combined together, and redundant proteins are excluded from the combined set with 180 proteins remaining in the list. The 180 proteins are culled by PISCES to eliminate the highly-similar proteins. The final data set contains 98 unique proteins (181 unique chains). After culling, this combined protein set is inspected manually to delete the chains which have only one transmembrane helix or no clear formation of a α-helical bundle. The final data set consists of 84 unique proteins (133 chains) ranging from 44 amino acid long to 1246 amino acid long. This is three times the size of the data set used by McAllister and Floudas [1]. The full list of proteins is listed in Table 1.
In order to determine the orientation of the two contacting helices for the construction of parallel and antiparallel probability sets, four planes are defined for each helix. They are formed by amino acid triplets (assuming amino acids i, i+3, i+4, i-3 and i-4 belong to helix m and amino acid j belongs to helix n), (i, j, i+3), (i, j, i+4), (i, j, i-3) and (i, j, i-4). Normal vectors of the planes formed by (i, j, i+3) and (i, j, i+4) are added together to form a new vector, and this new vector in perfect case should be normal to helix m and vector drawn from i to j. Similarly, another vector is formed for planes (i, j, i-3) and (i, j, i-4). A total of four vectors are generated for the helical pair and the orientation of the helical pair is determined by the angles between different combinations of the four vectors [68].
2.2 Mathematical Models
2.2.1 PAIRWISE contact prediction model
A two level formulation is used for the PAIRWISE prediction model. Level one predicts the PRIMARY contacts while level two focuses on the prediction of WHEEL contacts given the PRIMARY contacts. A PRIMARY contact forms between residue i and residue j on two different helices; while given a PRIMARY contact between residue pair (i,j), a WHEEL contact is a contact formed between residue i+3 or i+4 and residue j-3 or j-4 if these two helices form an anti-parallel contact, or between residue i+3 or i+4 and residue j+3 or j+4 for two parallel contacting helical pairs.
Level one maximizes the probability of the sum of residue-residue contacts as follows:
| (1) |
where m and n are indices for helices; is a binary variable, representing an anti-parallel (parallel) contact between helices m and n if ; is a binary variable, denoting a contact between residue i on helix m and residue j on helix n for ; is the PRIMARY contact probability that a residue pair (i,j) an anti-parallel (parallel) contact.
The constraints for this model are separated into five categories, including basic model constraints, geometrical constraints, model complexity, membrane protein observations and model features.
Basic model constraints
Eq. 2 specifies that a residue-residue contact binary variable can only be active when the two helices contact either in parallel or anti-parallel. On the other hand, when the sum of the binary variable is greater or equal to one, then one of the the variables and is allowed to be active; otherwise, if the sum of is zero, then both and should be disallowed. This is specified in Eq. 3.
| (2) |
| (3) |
Geometrical constraints
Firstly, a helical pair can only interact either in anti-parallel or parallel fashion, and this is expressed in Eq. 4.
| (4) |
Realizing that for the proteins with even number of helical segments (greater than 2), the first and last helices must contact in anti-parallel if they contact with each other; for the case of odd number of helices (greater than 2), the first and last helices should contact in parallel if a contact takes place between them. However, Eq. 7 in the paper by McAllister and Floudas only enforces the desired behavior for the case of subtract = 0, where subtract is a parameter used to limit the total number of helical contacts in the model. Thus, if a protein has 7 helices, there must be at most 6 anti-parallel contacts and if a protein has 6 helices, there must be at most 6 anti-parallel contacts. While valid, it does not produce the desired relationships for non-zero subtract values [1]. This equation is rewritten as two separate equations, Eq. 5 and Eq. 6, to impose the correct contacts between the first and last helices. In these two equations, N is the total number of helices. Eq. 5 disallows the parallel contact between the first and last helices if N is even, but is not enforced if N is odd; Eq. 6 disallows the anti-parallel contact between the first and last helices if N is odd, but is not enforced if N is even.
| (5) |
| (6) |
Kinks are prevented by Eq. 7. This equation says if residue pairs (i,j) and (k,l) both form a contact on a given helical pair m and n, the number of residues between residue i and k on helix m is required to be within three residues of the number between residue j and l on helix n, thus reducing the kinks.
| (7) |
Eq. 8 expresses that if helices hm and hn are predicted to be parallel with a contact (i,j), with i from helix hm and j from hn, and are both allowed to be active (k > i). This is true only when the condition ‘∀(i, j, k)|l > j, |(|diff(i, k)| − |diff(j, l)|)| < 3’ holds; otherwise, only one is allowed to be active. Similarly, for helices m and n contacting in anti-parallel fashion, Eq. 9 imposes this constraint.
| (8) |
| (9) |
Another geometrical constraint considers the situation when a small helix is contacting a longer helix, in this case the end of the first helix can not contact with the beginning of the second helix given the loop is few residue long. Eqs. 11 and 12 of McAllister and Floudas (2008) impose this constraint [1].
Model complexity constraints
The first model complexity constraint deals with the fact that there is a maximum number of contacts allowed between a helical pair m and n, this is written in Eq. 10.
| (10) |
For almost all proteins, counth(m) is set to 2, and for rare cases when a helix can not have 2 contacts, this parameter is set to 1.
Similarly, for a residue on a given helix m, only one contact is allowed between residue i on helix m and other residues on another helix n, as shown in Eq. 11.
| (11) |
Membrane protein observations
This model aims at predicting the most general topologies and most of transmembrane helices contacts in anti-parallel fashion for consecutive ones. Thus, the parallel contacts between neighboring transmembrane helices are disallowed as expressed in Eq. 12
| (12) |
Another constraint in this category says that the PRIMARY contact between two helices is disallowed if the overlap between the two helices is less than 90% of the shorter helix. This is based on the observation that transmembrane helices tend to line up in a similar fashion to form a bundle, see Eqs. 16 and 17 of McAllister and Floudas (2008) [1].
Model features
This model aims to predict the most important contacts between helices, thus it is necessary to impose a constraint on the maximum number of contacts allowed to be predicted for a helical pair. In Eq. 13, max_contact is the parameter to limit the total allowed contacts between two helices. It is often chosen as either 1 or 2 for different proteins. A smaller max_contact gives less predicted contacts from the model, however, they are more likely the most important contacts.
| (13) |
Besides the limit on the allowed contacts for two helices, a parameter subtract is introduced to limit the total number of possible helix-helix contacts in a protein. This is expressed in Eq. 14.
| (14) |
Since for most of proteins, counth(m) takes a value of 2, a subtract value of zero value allows the maximum number of inter-helical contacts to be the number of helices. A non-zero subtract reduces the total number of predicted helical contacts, thus resulting in looser helix packing.
The model also allows to generate a rank-ordered list of solutions, which is achieved using integer cuts which exclude previously found solutions from the feasible solution space [69]. The solution of each iteration is a unique set of binary variables ( , and ) including active variables and inactive variables. Thus, the best solution of previous iteration (inactive and active , , variables) is eliminated from the feasible solution space.
Level two formulation optimizes the WHEEL contact probability based on the PRIMARY contact predicted. This level formation can distinguish the PRIMARY contacts with same objective function values from level one optimization. The formulation expresses the objective function as follows:
| (15) |
| (16) |
| (17) |
| (18) |
| (19) |
where is a binary variable denoting the presence of a WHEEL contact between k and l given a PRIMARY contact between i and j on helices m and n respectively. represents the probability of forming a WHEEL contact between k and l given a PRIMARY contact between i and j on two helices interacting in anti-parallel (parallel) fashion.
Note that the original model by McAllister and Floudas (2008) allows only for the contacts between the neighboring helices to be predicted. This restricts the prediction ability for proteins with more complicated topology. For example, the helical contacts (topology) of calcium-transporting ATPase are very complicated, and non-neighboring transmembrane helices contact frequently. In this topology, helix 2 and helix 4 form a contact, helix 1 and helix 3 form a contact, helix 5 and helix 8 form a contact, etc. [63]. This restriction is changed in the proposed model here allowing n to n+2 helical contact to be predicted.
It should also be noted that the original model used subsets of residue space and subsets that connect the helices to reduce the computational costs. So instead of using i, j to refer residues, subi, subj are introduced. A parameter CONN is introduced denoting the subset of possible contact helical pairs. In the original model, CONN includes only the consecutive helical pairs, thus only neighboring helical contacts are allowed. For example, CONN=1 means possible contact between helices 1 and 2, CONN=2 means possible contact between helices 2 and 3. CONN=N (N is the number of helices) means possible contact between the first and last helices allowed to be predicted. Subi and subj are the sub spaces of i and j, and they are related by CONN value. For example, CONN=1, subi=5, subj=28 simply denotes that the residue 5 on helix 1 and residue 28 on helix 2 are in contact. This reduces the computational costs, however, it limits the capability of the model for predicting more complicated topologies, and every equation and constrain has to be expressed consistently with this subset definition. This modification to the model aims to enhance the model such that more difficult topologies of transmembrane helical proteins could be predicted.
2.2.2 TRIPLET contact prediction model
Similar to the PAIRWISE model, the TRIPLET model maximizes the sum of the TRIPLET contact probability to predict the TRIPLET contacts between helices allowed by the constraints. The objective function is expresses as,
| (20) |
In the above equation, is a binary variable representing a TRIPLET contact formed between residue i (a MAIN residue) on helix m, residue j (the first SECONDARY residue) on helix n and a third residue (the second SECONDARY residue) on helix n if t=1; otherwise, the contact is formed between residue i (the first SECONDARY residue) on helix m, residue j (a MAIN residue) on helix n and a third residue on helix m (the second SECONDARY residue) for the case t =2. Thus t is used to define the position of the second SECONDARY residue. is the probability that an anti-parallel (parallel) TRIPLET contact is formed between i, j and k where k is defined by the value of t.
The constraints for the TRIPLET model are mostly similar to those of the PAIRWISE model. These constraints are also grouped into five categories, basic model constraints, geometrical constraints, model complexity constraints, membrane protein observation related constraints and model feature constraints. A full description of these constraints is presented in the supplementary material and the paper by McAllister and Floudas [1].
The main difference between formulating the PAIRWISE and TRIPLET models is that the introduction of t to define the position of the second SECONDARY residue in the contact binary variable . This affects the formulation of all the constraints affected by the position of the second SECONDARY residue. Especially, the second model complexity constraint is affected mostly. This constraint basically states that a residue can mostly contact with one other residue on a specific helix. In order to have the similar constraint as in Eq. 11 for the PAIRWISE model, three rules are established. The first rule states that a MAIN residue in a TRIPLET contact can not serve either as a MAIN or SECONDARY residue in another TRIPLET contact; the second rule says two SECONDARY residues of a TRIPLET contact can not participate in TRIPLET contacts with multiple residues; the third rule states that a SECONDARY residue is disallowed to form more than two contacts. These rules are implemented through several constraints in the following.
The first rule is constrained by the following three equations, Eqs 21, 22 and 23.
| (21) |
This equation expresses the restriction that if residue j or j+1 serves as a MAIN residue on helix n in a TRIPLET contact between helix n and helix p, j or j+1 can not serve as a SECONDARY residue in another TRIPLET contacts.
| (22) |
Eq. 22 basically states that if j serves as a MAIN residue of a TRIPLET contact, it can not serves as another MAIN residue in a second TRIPLET contact. That is if ; and if .
Equation 23 has the similar effect as Eq. 21. It states that if residue j or j-1 serves as a MAIN residue on helix n in a TRIPLET contact between helix n and helix m, j or j-1 can not serve as a SECONDARY residue in another TRIPLET contacts.
| (23) |
Eq. 24 is used to impose the second rule. It states that if residue j and its neighbor residue serve as SECONDARY residues in a TRIPLET contact, then they can not participate in other TRIPLET contact as a SECONDARY residue pair.
| (24) |
The final rule is implemented in Eq. 25. This limits the overlapping TRIPLETs on one helix. This equation says if residue j is a SECONDARY residue on helix n of a TRIPLET between helix m and n, only one of its neighbor residue, j+1 or j-1, can participate in a TRIPLET contact.
| (25) |
Note that both the PAIRWISE and TRIPLET models are nonlinear, special care has to be taken to reformulate the objective functions from nonlinear form to linear. See the supplementary information of the paper by McAllister and Floudas [1] and the book by C. A. Floudas [69].
For additional information about the model, the readers are referred to the paper by McAllister and Floudas [1].
3 Results and Discussion
The calculation of accuracy depends on the definition of contact used. In this paper we use a threshold value (DisCutoff) of 14 Å to define a true contact, that is if the distance between two Cα atoms of a predicted contact is less than 14 Å this contact is classified as a true contact, otherwise it is a false contact. The accuracy is then calculated as the number of true contacts divided by total predicted contacts. A more frequently used contact definition is to use 8 Å as the threshold value between Cβ atoms of two amino acids [53, 70, 71]. Other definitions are also used, for example, Fuchs et al. defined a contact if the minimal distance between side chain or backbone heavy atoms is less than 5.5 Å [2]. Since the contact predictions will be used as distance restraints in our protein tertiary structure method, ASTRO-FOLD [23], we maintain the DisCutoff value of 14 Å for analysis. In order to include the false contacts with a small violation of DisCutoff value 14 Å, we also analyzed the accuracy for DisCutoff = 15 Å.
For the case when a protein in the test set is also in the data set used for constructing the probability set, a leave-one-out cross validation is used to exclude this protein from the training set for probability development. The test set is divided into three parts for analysis, proteins with three to five transmembrane helical segments, proteins with six to eight transmembrane helical segments and proteins with ten or more transmembrane helical segments. These three parts are referred to as TM3-5 proteins, TM6-8 proteins, and TM10 proteins, respectively.
3.1 Calculation of Accuracy
The accuracy is calculated for every parameter set. A parameter set consists of several parameters that can affect the prediction accuracy for a protein. The probability set (PROB) used in prediction is one parameter, and others include subtract (SUBT) and max_contact (MXCT) parameters. MXCT (max_contact) is the maximum number of allowed contacts between a transmembrane helical pair in the PAIRWISE and TRIPLET models, and is often chosen as 1 or 2 since the models aim at predicting the most probable amino acid interaction pairs. SUBT is an integer representing how many (m) to (n) helical contacts to remove from the maximal helical packing solution. A larger SUBT value leads to looser helical packing. A SUBT value of 0 or 1 is chosen for the prediction. PROB is the probability set, and takes one of the four probability sets, MIN-1N, MIN-2N, AL-P and AL-T. These four sets are described in Materials and Methods section. For simplicity, the parameter set is written as {PROB (probability set), MXCT (max_contact), SUBT (subtract)}. For example, a contact prediction for protein 2K73A includes the 16 different runs resulting from different combinations of parameter sets: {PROB=MIN-1N; MXCT=1; SUBT=0}, {PROB=MIN-1N; MXCT=1; SUBT=1}, {PROB=MIN-1N; MXCT=2; SUBT=0}, {PROB=MIN-1N; MXCT=2; SUBT=1}, {PROB=MIN-1N; MXCT=1; SUBT=0}, {PROB=MIN-2N; MXCT=1; SUBT=1}, {PROB=MIN-2N; MXCT=2; SUBT=0}, {PROB=MIN-2N; MXCT=2; SUBT=1}, {PROB=MIN-2N; MXCT=1; SUBT=0}, {PROB=AL-P; MXCT=1; SUBT=1}, {PROB=AL-P; MXCT=2; SUBT=0}, {PROB=AL-P; MXCT=2; SUBT=1}, {PROB=AL-P; MXCT=1; SUBT=0}, {PROB=AL-T; MXCT=1; SUBT=1}, {PROB=AL-T; MXCT=2; SUBT=0}, and {PROB=AL-T; MXCT=2; SUBT=1}.
For each parameter set, the prediction accuracy for DisCutoff is obtained through the following steps:
Step 1. Consider the predicted contacts in all iterations and calculate their frequencies (number of times predicted). This is based on the assumption that that the most essential inter-helical contacts in proteins have higher probabilities to be predicted.
Step 2. Take the top three most frequent predicted contacts for each helical pairs as the predicted contacts. If less than three contacts are predicted for a helical pair, take all the predicted contacts for this pair. Discard the predicted contact whose frequency is one. For the PAIRWISE model using the MIN-1N probability set, the prediction is analyzed separately for WHEEL and PRIMARY contacts.
Step 3. Calculate the prediction accuracy for this parameter set. If the predicted contact has an actual distance in the real structure below DisCutoff, this contact is a true prediction, otherwise, it is a false prediction. Prediction accuracy is defined as the total number of true predictions divided by the total predictions.
3.2 Effect of Probability Set on Accuracy
Comparing the average prediction accuracy for different probability sets allows to analyze the performance of different probability sets, and the average is calculated over the different parameter sets whose probability is the same. The average prediction accuracy is calculated for each probability set using different DisCutoff values (14 and 15 Å). For MIN-1N probability set, the PRIMARY and WHEEL contacts are analyzed separately. For example, for 2K73A, the average prediction accuracy for AL-P and DisCutoff = 14 Angstrom is calculated over four different parameter combinations: {PROB=AL-P, MXCT=1, SUBT=0}, {PROB=AL-P, MXCT=1, SUBT=1}, {PROB=AL-P, MXCT=2, SUBT=0}, and {PROB=AL-P, MXCT=2, SUBT=1}. The analysis is done separately for three groups of proteins, TM3-5, TM6-8 and TM10.
TM3-5 proteins
Table 2 presents the average prediction accuracy of different probability sets for TM3-5 proteins. The data show that the TRIPLET model outperforms the PAIRWISE model consistently. The TRIPLET model using the MIN-2N probability set has an average accuracy 55%, about 6% higher than that (48%) of primary contact of the corresponding the PAIRWISE model using the MIN-1N probability set (MIN-2N outperforms the accuracy for wheel contact using MIN-1N by a smaller margin of 2%). The TRIPLET model using the AL-T probability set shows a similar trend, that is the PAIRWISE model using AL-P is 3% lower in average accuracy. For each prediction model (PAIRWISE or TRIPLET), the probability sets developed show the advantage in prediction accuracy over the probability sets derived from the work by Adamian and Liang [63] and the work by Adamian et al. [64]. For example, the average prediction accuracy for MIN-2N using the TRIPLET model is 5% higher than the AL-T probability set using the same TRIPLET model; For the PAIRWISE model, although the MIN-1N probability set has an accuracy for PRIMARY contact of 48%, which is only 2% higher than the AL-P probability set, the average accuracy for WHEEL contact using MIN-1N is 6% higher than AL-P. The overall performance of the developed probability sets, MIN-1N and MIN-2N, is better than AL-P and AL-T for this group of proteins. The analysis of the accuracies for a DisCutoff value of 15 Å draws to the same conclusion as 14 Å. And it shows an average 5.4% increase in the average prediction accuracy compared with 14 Å, which means about 5.4% predicted contacts are between 14 to 15 Å in the real structure.
Table 2.
Average prediction accuracy using DisCutoff = 14 Å for TM3-5 proteins. The numbers in parenthesis are for DisCutoff = 15 Å. Second column shows the accuracy for Primary contact using MIN-1N probability set, and third column shows the accuracy for Wheel contact using MIN-1N probability set.
| Protein | MIN-1N(P) | MIN-1N(W) | AL-P | MIN-2N | AL-T |
|---|---|---|---|---|---|
| 1JB0L | 0.85(0.89) | 0.92(1.00) | 0.95(1.00) | 0.91(0.91) | 0.88(0.94) |
| 1NEKC | 0.79(0.79) | 0.80(0.87) | 0.51(0.65) | 0.85(0.92) | 0.50(0.57) |
| 1NEKD | 0.78(0.78) | 0.79(0.79) | 0.55(0.55) | 0.62(0.62) | 0.51(0.53) |
| 1VF5B | 0.18(0.18) | 0.12(0.26) | 0.18(0.18) | 0.26(0.32) | 0.10(0.12) |
| 2B76C | 0.15(0.15) | 0.16(0.33) | 0.25(0.25) | 0.24(0.24) | 0.11(0.11) |
| 2B76D | 0.52(0.65) | 0.93(0.93) | 0.68(0.68) | 0.46(0.49) | 0.38(0.38) |
| 2BHWA | 0.16(0.16) | 0.14(0.14) | 0.24(0.36) | 0.22(0.24) | 0.48(0.50) |
| 2FBWC | 0.51(0.51) | 0.48(0.55) | 0.47(0.50) | 0.41(0.41) | 0.33(0.39) |
| 2FBWD | 0.75(0.78) | 0.87(0.87) | 0.48(0.58) | 0.50(0.64) | 0.53(0.53) |
| 2OAUA | 0.41(0.44) | 0.36(0.52) | 0.51(0.61) | 0.44(0.46) | 0.37(0.38) |
| 1KQFC | 0.53(0.63) | 0.69(0.72) | 0.48(0.57) | 0.59(0.74) | 0.52(0.56) |
| 1ORQC | 0.29(0.32) | 0.18(0.30) | 0.12(0.14) | 0.31(0.31) | 0.24(0.30) |
| 1VF5A | 0.44(0.52) | 0.56(0.65) | 0.56(0.61) | 0.61(0.75) | 0.65(0.81) |
| 1YEWC | 0.79(0.87) | 0.76(0.79) | 0.64(0.70) | 0.24(0.47) | 0.37(0.66) |
| 2A79B | 0.19(0.19) | 0.19(0.19) | 0.05(0.05) | 0.31(0.37) | 0.38(0.38) |
| 2BG9A | 0.45(0.51) | 0.63(0.66) | 0.58(0.61) | 0.66(0.70) | 0.56(0.75) |
| 2BL2A | 0.98(1.00) | 0.69(0.79) | 0.79(0.79) | 0.95(0.95) | 0.91(0.92) |
| 2HI7B | 0.25(0.27) | 0.38(0.42) | 0.22(0.28) | 0.65(0.65) | 0.36(0.42) |
| 2UUHA | 0.62(0.62) | 0.61(0.66) | 0.75(0.78) | 0.55(0.61) | 0.70(0.77) |
| 1AIGL | 0.51(0.51) | 0.41(0.41) | 0.30(0.51) | 0.64(0.64) | 0.49(0.51) |
| 1EYSM | 0.23(0.38) | 0.47(0.52) | 0.57(0.61) | 0.34(0.44) | 0.56(0.67) |
| 1FFTC | 0.35(0.42) | 0.53(0.59) | 0.36(0.39) | 0.71(0.79) | 0.53(0.71) |
| 1Q16C | 0.45(0.62) | 0.56(0.62) | 0.29(0.40) | 0.70(0.76) | 0.68(0.74) |
| 2AXTA | 0.59(0.62) | 0.55(0.57) | 0.55(0.58) | 0.57(0.61) | 0.46(0.50) |
| 2AXTD | 0.40(0.40) | 0.53(0.53) | 0.56(0.61) | 0.54(0.55) | 0.50(0.55) |
| 2BS2C | 0.20(0.44) | 0.08(0.24) | 0.31(0.35) | 0.65(0.87) | 0.70(0.82) |
|
| |||||
| Avg. | 0.48(0.53) | 0.52(0.57) | 0.46(0.51) | 0.54(0.59) | 0.49(0.56) |
For some proteins, our prediction accuracy is even above 90%, including 1JB0L using MIN-2N, AL-P and MIN-1N for WHEEL contact, 2BL2A using MIN-2N and AL-T and MIN-1N for PRIMARY contact. 1JB0L is a three transmembrane helical protein with three helices contacting with each other in anti-parallel fashion forming a very compact structure. 2BL2A has four transmembrane helices with consecutive helices contacting in anti-parallel fashion and helices 1 and 4 positioning at the opposite corners of the bundle. Our enhanced model allows the contact prediction between helix i and helix i+2, a prediction run with parameter set {MIN-1N; MXCT=2; SUBT=1} correctly predicted the contacts between helix 2 and helix 4, and between helix 1 and 3. However, for a protein with a rare topology, it is difficult for our model to predict. An example is four transmembrane helical protein 2A79B. Instead of forming a helical bundle, the four helices form a mostly planar structure with helix 1 and helix 2 from a parallel contact and helices 1 and 2 are far away from helices 3 and 4. Since our model assumes the anti-parallel contact between neighboring helices and maximizes the contact probability, the prediction accuracy of our model was low.
TM6-8 proteins
Table 3 shows the average accuracy for the TM6-8 proteins. Compared with the proteins in Table 2, these proteins have higher topological complexity, thus making the contact prediction more difficult. It can be seen from comparing Table 2 and Table 3 that the prediction accuracies of TM6-8 proteins for different probability sets are lower than the corresponding prediction accuracies of TM3-5 proteins. The average accuracy of TM6-8 proteins over all the probability sets is 43.8 %. Compared with 49.8 % of TM3-5 proteins, the prediction accuracy has dropped by 6% for a DisCutoff value of 14 Å. The accuracies of MIN-1N and AL-P are 40% and 38%, respectively, both of which are dropped by 8% compared with those of TM3-5 proteins. The TRIPLET model shows a smaller decrease in prediction accuracy. The accuracies of the probability sets MIN-2N and AL-T are 49% and 48%, only reduced by 5% and 1%, respectively. It is surprising that AL-T probability set performs well for TM6-8 proteins. Some of the conclusions for TM3-5 proteins are still valid for TM6-8 proteins. For example, the TRIPLET model using the MIN-2N and AL-T probability sets perform better than the PAIRWISE model using the MIN-1N and AL-P probability sets; and the probability sets MIN-1N and MIN-2N outperforms the AL-P and AL-T probability sets, although the accuracy for MIN-2N is only 1 % higher than AL-T. Also the accuracies for DisCutoff = 15 Å have the same tendency as 14 Å.
Table 3.
Average prediction accuracy using DisCutoff = 14 Å for TM6-8 proteins. The numbers in parenthesis are for DisCutoff = 15 Å. Second column shows the accuracy for Primary contact using MIN-1N probability set, and third column shows the accuracy for Wheel contact using MIN-1N probability set.
| Protein | MIN-1N(P) | MIN-1N(W) | AL-P | MIN-2N | AL-T |
|---|---|---|---|---|---|
| 1FX8A | 0.41(0.49) | 0.42(0.48) | 0.29(0.33) | 0.35(0.36) | 0.35(0.44) |
| 2AXTB | 0.19(0.19) | 0.25(0.25) | 0.36(0.36) | 0.43(0.43) | 0.56(0.56) |
| 2AXTC | 0.21(0.25) | 0.27(0.27) | 0.20(0.20) | 0.25(0.25) | 0.33(0.38) |
| 2C3EA | 0.35(0.45) | 0.30(0.42) | 0.07(0.08) | 0.45(0.59) | 0.37(0.49) |
| 2EVUA | 0.28(0.31) | 0.28(0.34) | 0.21(0.28) | 0.37(0.38) | 0.35(0.37) |
| 2HYDA | 0.59(0.59) | 0.68(0.75) | 0.34(0.42) | 0.54(0.63) | 0.60(0.62) |
| 2IC8A | 0.30(0.42) | 0.30(0.32) | 0.35(0.47) | 0.43(0.48) | 0.41(0.54) |
| 2NR9A | 0.27(0.37) | 0.27(0.29) | 0.47(0.54) | 0.36(0.43) | 0.52(0.64) |
| 2O9DA | 0.38(0.44) | 0.53(0.53) | 0.43(0.45) | 0.30(0.30) | 0.48(0.56) |
| 2ONKC | 0.38(0.44) | 0.26(0.35) | 0.27(0.30) | 0.56(0.59) | 0.34(0.35) |
| 3B4RB | 0.58(0.62) | 0.58(0.84) | 0.46(0.52) | 0.39(0.45) | 0.09(0.09) |
| 1M0KA | 0.59(0.64) | 0.70(0.77) | 0.58(0.68) | 0.70(0.82) | 0.94(1.00) |
| 1QLEC | 0.43(0.50) | 0.44(0.50) | 0.37(0.50) | 0.56(0.65) | 0.44(0.49) |
| 1U19A | 0.47(0.63) | 0.59(0.79) | 0.58(0.64) | 0.73(0.86) | 0.72(0.81) |
| 1XIOA | 0.59(0.62) | 0.61(0.85) | 0.63(0.71) | 0.71(0.74) | 0.75(0.80) |
| 1YEWB | 0.42(0.50) | 0.56(0.56) | 0.56(0.59) | 0.53(0.60) | 0.43(0.50) |
| 2F93A | 0.71(0.73) | 0.68(0.76) | 0.63(0.67) | 0.63(0.70) | 0.72(0.74) |
| 2JAFA | 0.58(0.71) | 0.68(0.80) | 0.59(0.65) | 0.82(0.90) | 0.77(0.83) |
| 1BCCC | 0.32(0.40) | 0.30(0.51) | 0.30(0.41) | 0.49(0.53) | 0.37(0.42) |
| 2FYNA | 0.28(0.35) | 0.28(0.29) | 0.27(0.36) | 0.39(0.44) | 0.31(0.35) |
| 2NWLA | 0.15(0.15) | 0.23(0.21) | 0.09(0.16) | 0.20(0.21) | 0.20(0.20) |
|
| |||||
| Avg. | 0.40(0.47) | 0.44(0.52) | 0.38(0.44) | 0.49(0.54) | 0.48(0.53) |
The best prediction is for 1M0KA using the AL-T probability set with an accuracy of 94%. This protein is a seven transmembrane helical bundle and is the K intermediate of bacteriorhodopsin [72]. The model with parameter set {AL; MACT=2; SUBT=1} successfully predicted the contacts between helix 3 and helix 5 as well as many other contacts. Only one false contact between 14A and 207L is predicted as can be seen from Fig. 1. 14A and 207L are on the opposite side of helix 1 and helix 7. The contact prediction for 2NWLA is least successful, with 20% for the TRIPLET model using both the MIN-2N and AL-T probability sets. 2NWLA is a eight transmembrane helical protein containing two helical membrane loops in the center of the protein which makes transmembrane helical segments to spread out. Helix 5 is even between helix 1 and helix 2. This complexity makes 2NWLA have an irregular topology.
Figure 1.
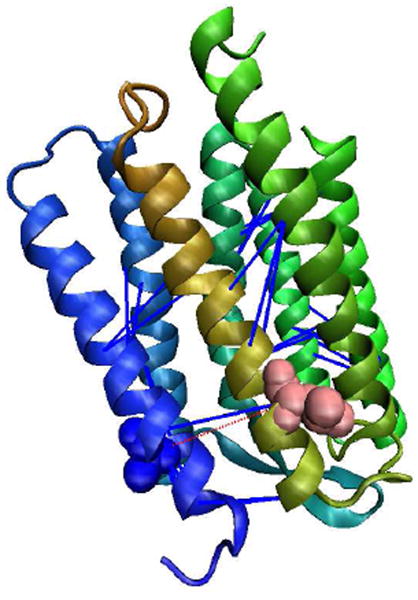
A cartoon illustrating the residue contact prediction for 1M0KA. Blue lines show the correct predictions while the red dotted line represents the false prediction between 207L (pink) and 14A (blue).
TM10 proteins
While the TM6-8 proteins already showed great topological complexities, the greatest challenge for testing the prediction ability of our models and the probability sets comes with the proteins that have even more transmembrane helical segments. Since there are no nine transmembrane helical membrane proteins in the test set from Fuchs et al. [2], all the proteins in Table 4 have at least 10 transmembrane helical segments. Out of the 18 proteins in Table 4, seven proteins have 10 transmembrane helical segments, two proteins have 11 transmembrane helical segments, eight proteins have 12 transmembrane helical segments, and one protein has 13 transmembrane helical segments.
Table 4.
Average prediction accuracy using DisCutoff = 14 Å for TM10 proteins. The numbers in parenthesis are for DisCutoff = 15 Å. Second column shows the accuracy for Primary contact using MIN-1N probability set, and third column shows the accuracy for Wheel contact using MIN-1N probability set. Last column shows the number of transmembrane helices of the proteins.
| Protein | MIN-1N(P) | MIN-1N(W) | AL-P | MIN-2N | AL-T | # Helices |
|---|---|---|---|---|---|---|
| 1L7VA | 0.44(0.56) | 0.46(0.52) | 0.39(0.45) | 0.33(0.40) | 0.49(0.54) | 10 |
| 1RH5A | 0.30(0.42) | 0.32(0.38) | 0.40(0.41) | 0.28(0.37) | 0.47(0.48) | 10 |
| 2AGVA | 0.43(0.45) | 0.32(0.50) | 0.24(0.28) | 0.35(0.49) | 0.52(0.62) | 10 |
| 2EXWA | 0.29(0.32) | 0.35(0.35) | 0.18(0.20) | 0.27(0.31) | 0.21(0.23) | 10 |
| 2NMRA | 0.57(0.60) | 0.59(0.61) | 0.53(0.64) | 0.47(0.52) | 0.41(0.43) | 10 |
| 3B8CA | 0.32(0.46) | 0.47(0.55) | 0.43(0.43) | 0.52(0.54) | 0.46(0.51) | 10 |
| 3B8EA | 0.56(0.65) | 0.57(0.61) | 0.49(0.51) | 0.42(0.45) | 0.33(0.38) | 10 |
| 1JB0A | 0.54(0.54) | 0.54(0.54) | 0.44(0.44) | 0.53(0.54) | 0.56(0.62) | 11 |
| 2B2FA | 0.51(0.61) | 0.52(0.58) | 0.57(0.64) | 0.52(0.60) | 0.45(0.45) | 11 |
| 1FFTA | 0.59(0.73) | 0.66(0.73) | 0.55(0.59) | 0.62(0.67) | 0.59(0.72) | 12 |
| 1PW4A | 0.22(0.28) | 0.30(0.36) | 0.34(0.40) | 0.34(0.42) | 0.47(0.50) | 12 |
| 1ZCDA | 0.31(0.40) | 0.40(0.45) | 0.23(0.35) | 0.37(0.46) | 0.30(0.32) | 12 |
| 2A65A | 0.13(0.18) | 0.10(0.13) | 0.12(0.21) | 0.24(0.30) | 0.16(0.21) | 12 |
| 2CFPA | 0.23(0.30) | 0.26(0.30) | 0.17(0.19) | 0.37(0.41) | 0.31(0.35) | 12 |
| 2GFPA | 0.23(0.26) | 0.28(0.32) | 0.20(0.29) | 0.25(0.33) | 0.17(0.21) | 12 |
| 2GIFA | 0.30(0.39) | 0.23(0.35) | 0.31(0.38) | 0.13(0.25) | 0.40(0.48) | 12 |
| 2GSMA | 0.57(0.64) | 0.60(0.78) | 0.63(0.75) | 0.66(0.80) | 0.86(0.94) | 12 |
| 1XMEA | 0.54(0.60) | 0.54(0.56) | 0.51(0.59) | 0.49(0.56) | 0.60(0.67) | 13 |
|
| ||||||
| Avg. | 0.39(0.47) | 0.42(0.48) | 0.37(0.43) | 0.40(0.47) | 0.43(0.48) | |
It is shown in Table 4 that MIN-2N has a prediction accuracy 40%, which is 1% higher than the MIN-1N probability set for the PRIMARY contact. However, a claim can not be made that MIN-2N is better than MIN-1N especially when considering the average accuracy of MIN-1N combining PRIMARY and WHEEL contacts. AL-T indeed shows better prediction ability than AL-P; and in fact AL-T is the best among all the probability sets for TM10 proteins. For example, by using the TRIPLET model with the AL-T probability set, an accuracy of 86% is achieved for protein 2GSMA. 2GSMA is a 12 transmembrane helical bundle with the consecutive helices interacting in an anti-parallel pattern and the last helix form a contact with the first helix. Since our models predict the n to n+1 and n to n+2 helical contacts, the prediction accuracies for this protein is high. For the proteins with irregular topologies, the prediction accuracy is reduced. For example, the accuracy of 2A65A is less than 24% for all the probability sets, and the transmembrane helices in 2A65A have irregular pattern caused by the big tilt angles.
A surprising finding in Table 4 is that the prediction accuracies for the TRIPLET model has been decreased more than PAIRWISE model, compared with the accuracies for TM6-8 proteins. MIN-2N has the largest drop in prediction accuracy, 9% from 49% for TM6-8 proteins to 40% for TM10 proteins. The second largest drop is for the AL-T probability set, 5%. However, the probabilities sets for the PAIRWISE model show a slight decrease, ranging from 1% to 2 %. This drop in prediction accuracy for the TRIPLET model brings the prediction performance for the TRIPLET and PAIRWISE models closer.
The overall performance of the TRIPLET model across all the test proteins is better than the PAIRWISE model. Which probability set should be used for the TRIPLET model depends on the complexity of the system studied. While for proteins with easy topology (see Table 2), MIN-2N outperforms the AL-T probability set; as the complexity of the system increases, the prediction ability of the MIN-2N is decreasing faster than AL-T. For TM10 proteins with greatest complexity, AL-T performs better than MIN-2N, thus should be used. For TM6-8 proteins, MIN-2N is slightly preferred than AL-T by 1%.
3.3 Effect of MXCT Parameter on Accuracy
A MXCT value of 2 allows the model to predict more contacts between helices. But how does MXCT value affect the contact prediction accuracy? Further analysis focuses on the effect of MXCT parameter on the average prediction accuracy. This analysis is important since for a blind prediction when the three dimensional structure is unknown, an optimal prediction using different parameters should be chosen such that the expected prediction accuracy is maximum.
The average prediction accuracy is calculated over two runs sharing the same MXCT value but different SUBT values for MIN-2N and AL-T probability sets. These two probability sets were chosen because they outperform other probability sets. The calculation of accuracy uses the DisCutoff value 14 Å.
In Table 5, the accuracy of MXCT=2 using the AL-T probability set is the same as that of MXCT=1 for the first two groups of proteins. For TM3-5 membrane proteins and TM6-8 proteins, the accuracies are 49% and 48%, respectively. For proteins with more transmembrane helices, using MXCT=2 generates a slightly higher accuracy than using MXCT=1 for AL-T probability sets. On the other hand, for the MIN-2N probability set, using parameter MXCT=2 uniformly results in better prediction accuracies than using MXCT=1 for all three groups of proteins with different complexities.
Table 5.
The average prediction accuracy for proteins with different complexities using MXCT=2. The numbers in parenthesis are average prediction accuracies for MXCT=1. The calculation of accuracy uses DisCutoff=14 Å.
| Proteins | MIN-2N | AL-T |
|---|---|---|
| TM3-5 | 0.54(0.53) | 0.49(0.49) |
| TM6-8 | 0.49(0.48) | 0.48(0.48) |
| TM10 | 0.42(0.38) | 0.44(0.43) |
The results in Table 5 also agree with the analysis of the effect of probability sets on prediction accuracy. MIN-2N is a better choice for proteins with easy topologies for both MXCT values, and AL-T performs better for proteins with greatest complexities (i.e., with ten or more transmembrane helices) for both MXCT values. For the proteins with six to eight transmembrane helices, MIN-2N with MXCT=2 has an accuracy of 49 %, slightly favored over AL-T with MXCT=2 (48 %).
In conclusion, using MXCT=2 is a better choice for the MIN-2N probability set; MXCT=2 and MXCT=1 show the same effect on the prediction accuracy for the AL-T probability set (only 1% difference in prediction accuracy is observed for TM10 proteins).
3.4 Effect of SUBT Parameter on Accuracy
This part focuses on the effect of the SUBT parameter on the contact prediction accuracy for the proteins with different topological complexities. Average accuracy is calculated over two runs sharing the same SUBT value and the same probability set but different MXCT values (MXCT=1 and MXCT=2). Following similar analysis as for the MXCT parameter, only accuracies for MIN-2N and AL-T probability sets were calculated since they provide higher contact prediction accuracy compared to other probability sets.
Table 6 shows the average prediction accuracy for SUBT=1 and SUBT=0 (in parenthesis). We can observe that using parameter SUBT=0 generates higher (or even) prediction accuracies for all the cases except for proteins with three to five transmembrane helices for the MIN-2N probability set. The MIN-2N probability set using SUBT=1 has an average accuracy of 56%, which is 4% more than the accuracy by using SUBT=0. Thus, SUBT=1 is a better choice than SUBT=2 for TM3-5 proteins. For TM6-8 proteins, using SUBT=0 results in higher prediction accuracies than that of using SUBT=1. On the other hand, for proteins with ten or more transmembrane helices, there is no difference in prediction accuracy between those of using SUBT=1 and SUBT=0; however, since using SUBT=0 allows more contacts to be predicted, it is a preferred choice.
Table 6.
The average prediction accuracy for proteins with different complexities by using SUBT=1. The numbers in parenthesis are average prediction accuracies for SUBT=0. The calculation of accuracy uses DisCutoff=14 Å.
| Proteins | MIN-2N | AL-T |
|---|---|---|
| TM3-5 | 0.56(0.52) | 0.49(0.50) |
| TM6-8 | 0.48(0.49) | 0.47(0.49) |
| TM10 | 0.40(0.40) | 0.43(0.43) |
3.5 Summary of Contact Predictions
In summary, the number of transmembrane helices of the protein determines which probability sets should be used. For TM3-5 proteins, the MIN-2N probability set out-performs other probability sets in terms of the average prediction accuracy. For TM6-8 proteins, the MIN-2N probability set is a slightly better choice than the AL-T probability set, both of which generated higher prediction accuracies compared to the PAIRWISE probability sets. TM10 proteins have the greatest complexity in topology. The probability sets for the TRIPLET model generated higher prediction accuracies than those for the PAIRWISE model. The AL-T probability set is preferred to use for contact prediction than the MIN-2N probability set.
After the probability set is chosen, other parameters should be selected to use for the contact prediction. Based on the analysis, a parameter value of MXCT=2 should be used when the MIN-2N probability is used. For the case when the AL-T probability set is used, different values of MXCT (1 or 2) have same effect on prediction accuracies, however, due to the fact that using MXCT=2 lead into more predicted contacts, MXCT=2 is preferred. The parameter value SUBT=1 should be used when the MIN-2N probability set is used in the contact prediction for TM3-5 proteins. For all other situations, SUBT=0 should be used since it allows more contacts to be predicted while the same or even higher prediction accuracy than that of SUBT=1 are achieved.
Combining the analysis of probability sets, the MXCT and SUBT parameter values, it is suggested that the following should be used for different proteins with different topological complexities. The contact prediction of TM3-5 proteins should use the parameter set {MIN-2N; MXCT=2; SUBT=1}. For TM6-8 proteins, {MIN-2N; MXCT=2; SUBT=0} is a better choice; and {AL-T; MXCT=2; SUBT=0} is the best choice for contact prediction in TM10 proteins.
3.6 Predictions with Known Transmembrane Helical Information
Five proteins are chosen as a first test set of the proposed method for contact prediction. The PDB codes for the five proteins are, 2K73A, 1YEWC, 3EMLA, 1H2SA, 1F88A. If the test protein already exists in the training protein set, this protein is excluded for building the probability sets. The transmembrane helical information is obtained from PDBTM [62]. 2K73A and 1YEWC are four transmembrane helical proteins, and the other three are seven transmembrane helical proteins. According to the proposed method, {MIN-2N; MXCT=2; SUBT=1} is used for 2K73A and 1YEWC ; while {MIN-2N; MXCT=2; SUBT=0} is used for 3EMLA, 1H2SA and 1F88A.
The contact prediction accuracies obtained for these proteins are, 1YEWC: 25%, 2K73A: 54%, 3EMLA: 61%, 1H2SA: 77% and 1F88A 62 %. The average accuracy of the five proteins is 56%. 1YEWC is a membrane protein that catalyses the biological oxidation of methane to methanol and the knowledge of how this process happens can help to develop an alternative energy source [73]. The reason for this low prediction accuracy is that the topology of 1YEWC is a four helical bundle, with helix 1 and helix 4 interacting in the opposite corners of the bundle, and helix 2 and helix 3 being separated by helix 4. This topology causes all the predicted contacts between helix 2 and helix 3 to be false contacts, and leads into low prediction accuracy.
The best contact prediction is for protein 1H2SA. 1H2SA is a sensory rhodopsin with seven transmembrane helices [74]. The contacts predicted for 1H2SA from the parameter set {MIN-2N; MXCT=2; SUBT=0} are listed in Table 7. The prediction accuracy of 1H2SA is 77%. Note in the table the contact between 12A and 49V happens twice, this is because this contact is predicted by two different TRIPLET contacts. After subtracting 1 from the total number of contacts, the prediction accuracy for 1H2SA is 76%. The average distance for true contact prediction is 9.32 Å and while the average distance for false contact prediction is 15.85 Å. Figure 2 shows the correct predicted contacts and false contacts in this protein.
Table 7.
A prediction result for 1H2SA by using parameter set {MIN-2N; MXCT=2; SUBT=1}. Res1 is the MAIN residue and Res2 and Res3 are the SECONDARY residues in the TRIPLET contact.
| Res1 | Res2 | Distance | Res1 | Res3 | Distance |
|---|---|---|---|---|---|
| 40L | 20L | 10.10 | 40L | 21A | 9.80 |
| 12A | 49V | 7.20 | 12A | 50A | 7.80 |
| 12A | 48A | 4.70 | 12A | 49V | 7.20 |
| 70A | 55A | 12.40 | 70A | 56L | 13.10 |
| 77I | 46I | 10.70 | 77I | 47A | 10.60 |
| 84V | 40L | 11.20 | 84V | 41V | 14.30 |
| 70A | 125A | 19.40 | 70A | 126L | 16.20 |
| 91A | 148S | 5.40 | 91A | 149A | 3.80 |
| 159L | 212A | 7.10 | 159L | 213L | 10.30 |
| 168V | 202L | 15.20 | 168V | 203V | 12.50 |
| 23A | 214D | 14.20 | 23A | 215A | 15.80 |
| 25A | 214D | 10.20 | 25A | 215A | 11.90 |
| 4L | 195A | 8.40 | 4L | 196L | 9.80 |
Figure 2.
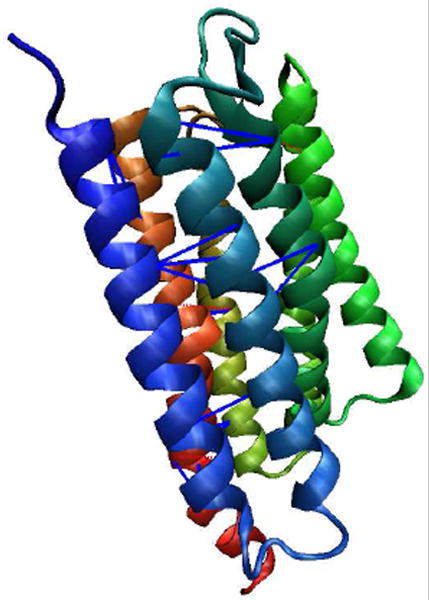
A cartoon illustrating the residue contact prediction for 1H2SA. Blue lines show the correct predictions while the red dotted lines represent the false predictions.
1F88A and 3EMLA are also seven transmembrane helical bundle proteins. 1F88A is bovine rhodopsin and is well-studied [75]; 3EMLA is human A2A adenosine receptor recently resolved by Jaakola et al. [76]. For these two proteins, the prediction accuracies are close to each other, 62% and 61%, respectively.
3.7 Predictions with Unknown Transmembrane Helical Information
One of the goals of contact prediction is to provide the useful distance constraints for helping determine the three dimensional structure of a protein. The second set of test proteins used in this section is released later than Feb 22, 2009 in MPDB [61] and in PDBTM [62]. To avoid the sequence similarity between the proteins for building the probability set and the proteins for testing, PISCES [65] is used to ensure the non-redundancy of testing proteins against the training set (maximum allowable sequence identity of 35% was used for all of the comparisons). Each of the downloaded proteins is subject to the similarity check and 42 non-redundant proteins are obtained from these two membrane protein data banks.
In true blind predictions no information is known for transmembrane helical segments and their contacts. The transmembrane helical information for these proteins is predicted by MEMSAT3 [77]. MEMSAT3 predicts transmembrane protein topology using neural networks and the method is found to predict both the correct topology and the locations of transmembrane segments for 80% of the test proteins [77]. It is also important to study the contact prediction of proteins with difficult topologies, thus proteins with less than 3 transmembrane helices are excluded. Six out of the 42 non-redundant proteins have more than three transmembrane helices: 2ZY9A (5 helices, 427 amino acids), 2W1PA (6 helices, 263 amino acids), 3CN5A (6 helices, 237 amino acids), 3KCUA (7 helices, 252 amino acids), 3IXZA (10 helices, 998 amino acids) and 3K3FA (10 helices, 332 amino acids). The MEMSAT3 predicted transmembrane helical segments and PDBTM obtained transmembrane helical segments are listed in Tables 10 and 11 of the supplementary material.
Based on the number of transmembrane helices, {MIN-2N; MXCT=2; SUBT=0} is used for predicting the inter-helical residue contacts of proteins 2W1PA, 3KCUA and 3CN5A. The parameter set {AL-T; MXCT=2; SUBT=0} is used for protein 3IXZA and 3K3FA. The parameter set {MIN-2N; MXCT=2; SUBT=1} is used for protein 2ZY9A. The prediction accuracies obtained are, 2ZY9A: 73%, 3KCUA: 21%, 2W1PA: 46%, 3CN5A: 64%, 3IXZA: 77% and 3K3FA: 83%. The average prediction accuracy for the six proteins is 60.7%. The detailed residue contacts predicted for protein 3IXZA are shown in Table 8, and predicted contacts for other proteins are listed in Tables 12-16 of the supplementary material.
Table 8.
The proposed contact prediction for 3IXZA. Res1 is the MAIN residue and Res2 and Res3 are the SECONDARY residues in the TRIPLET contact.
| Res1 | Res2 | Distance | Res1 | Res3 | Distance |
|---|---|---|---|---|---|
| 77L | 109A | 7.40 | 77L | 110L | 5.30 |
| 118G | 70L | 5.80 | 118G | 71A | 3.90 |
| 118G | 272L | 9.20 | 118G | 273A | 8.30 |
| 278A | 111I | 3.70 | 278A | 112A | 3.00 |
| 111I | 279T | 6.00 | |||
| 277G | 311L | 13.40 | 277G | 312A | 12.30 |
| 275L | 311L | 9.00 | 275L | 312A | 8.00 |
| 309G | 277G | 9.30 | 309G | 278A | 11.50 |
| 761L | 309G | 9.10 | 761L | 310L | 12.30 |
| 761L | 311L | 15.30 | 761L | 312A | 14.30 |
| 758I | 312A | 13.10 | 758I | 313T | 11.80 |
| 932A | 832G | 3.70 | 932A | 833A | 5.00 |
| 940G | 838A | 5.40 | 940G | 839G | 2.90 |
| 939I | 970G | 10.40 | 939I | 971L | 14.10 |
| 972L | 73G | 32.30 | 972L | 74L | 31.40 |
| 972L | 70L | 39.90 | 972L | 71A | 38.40 |
The highest accuracies are obtained for proteins 3IXZA (77%) and 3K3FA(83%) even though they have a much more complicated topology (10 transmembrane helices). 3IXZA is an proton pump responsible for generating a proton gradient across the gastric membrane. Its structure is resolved at 6.5 A resolution by electron crystallography [78]. The predicted contacts of 3IXZA are shown in Table 8. As shown in Table 8, the proposed method is able to predict some important short-range contacts, such as 839G-940G of 2.9 Å, 71A-118G of 3.9 Å, 111I-278A of 3.7 Å. The worst false predictions are for 70L-972L, 73G-972L, 71A-972L and 74L-972L (all above 30 Å). These correspond to the residue contact pairs of helix 1 and helix 10. Helix 1 and helix 10 do not form a contact and are separated far away from each other which causes the false predictions for 70L-972L, 73G-972L, 71A-972L and 74L-972L.
The lowest prediction accuracy is obtained for protein 3KCUA. This is partially due to the poor transmembrane helical segment prediction from MEMSAT3. From the membrane protein data bank PDBTM, seven transmembrane helical segments exist for protein 3KCUA, they are 8Y-31T, 35P-55V, 87L-113A, 118G-151V, 165F-176A, 182S-198F and 217L-241L (the amino acid IDs are renumbered so that the ID 1 corresponds to the first amino acid in the PDB structure); on the other hand, however, MEMSAT3 predicted 6 transmembrane helical segments for 3KCUA: 8Y-31T, 40K-64S, 85N-109E, 125A-148C, 163K-187F and 220M-244L. Clearly there is one transmembrane helix missing (helix 6: 182S-198F) in the prediction. This causes all the predictions between helix 5 and helix 6 to be wrong, for example contact 168V-241L with a distance of 19.70 Å, contact 175V-233G with a distance of 15.5 Å.
By using predicted transmembrane helical information, our proposed contact prediction method performed with an average contact accuracy of 60.7% on the six non-redundant transmembrane proteins with complex topologies. Testing on these six proteins is far from enough to conclude that our method is robust, however, it does show some potential, and this method will benefit from the growing number of membrane proteins released each year.
3.8 Comparison with a Support Vector Machine Method: TMhit
This section compares the performance of our method with a support vector machine method, TMhit [3]. TMhit is an online server and can predict residue contacts and helical pair interactions using support vector machine. An average accuracy of 44.8% was reported for TMhit when tested on an independent protein set (Table 1 in Ref. [3]). However a direct comparison of these two methods could provide more relevant and valuable information.
TMhit method was evaluated on the same six proteins used in the above section. These six proteins are released after Feb. 2009 and each of them was subject to a non-redundancy check against the training set of proteins [65]. Given that the training set of proteins is a very comprehensive and non-redundant, and TMhit was trained on the proteins released before Feb. 2009, these six proteins are independent proteins to TMhit training proteins.
The comparison results are shown in Table 9. The average prediction accuracy over the six proteins is 60.7% for our proposed approach, which is better than the highest accuracy 41.9% of TMhit. The best prediction accuracy for TMhit method is for L/5, 41.9%, slightly lower than the accuracy 44.8% reported in Table 1 of Ref. [3]. Although our method only uses residue contact propensities and TMhit uses many other features as input to its support vector machine (such as evolutionary profile), our model outperforms TMhit on average. However, TMhit performs better for proteins 2ZY9A and 2W1PA than our method, especially for 2ZY9A. TMhit predicts residue contacts for 2ZY9A with an accuracy of 100% for both L/5 and Top20 predicted residue contacts. On the other hand, our method performs much better for membrane proteins with complex topologies, such as proteins 3IXZA and 3K3FA, both having 10 transmembrane helical segments. Protein 3KCUA has the lowest prediction accuracy for both our method and TMhit method. This is due to the poor prediction of transmembrane helical segments by MEMSAT3 [77]. Both methods could benefit from an improved prediction power of helical segments for transmembrane proteins. The TMhit predicted residue contacts are listed in Tables 17-23 of the supplementary material.
In terms of computational cost, it takes about 2 minutes on average (for the 6 test cases) to receive the result from TMhit server. The proposed method takes about 5 minutes on average to predict the contact for a protein (CPU: Intel(R) Core(TM)2 Quad 2.83GHz (one core is used)).
4 Conclusions
Contact prediction for globular proteins has helped protein structure prediction in various ways, however the three dimension structure prediction for membrane proteins are relatively limited either by the limited experimental data in Protein Data Bank or by the difficulty to model or consider the surroundings around membrane proteins. This work is based on two mixed integer linear programing optimization models which focus on the contact prediction in transmembrane alpha-helical membrane proteins, and aims to predict high-quality amino acid contact constraints between transmembrane helical segments that can be used for three dimensional structure prediction for membrane proteins. In order to do so, a new enhanced data set has been built and the several important modifications were made to the PAIRWISE and TRIPLET contact prediction models. These modifications allows the model to predict more important contacts between transmembrane helices.
A strategy was proposed to predict the inter-helical contacts by which different parameter sets are used for different transmembrane alpha-helical proteins with different topological complexities. In order to test our models on blind cases, six non-redundant proteins with complicated topologies are used. By using MEMSAT3 to predict the transmembrane helical information for the proteins, our model was able to predict the contacts for all of the proteins with an average prediction accuracy of 60.7%. This outperforms on average a support vector machine method, TMhit [3]. The presented residue contact prediction method for membrane proteins shows great potential and it can help structure prediction of membrane proteins.
Supplementary Material
Acknowledgments
CAF gratefully acknowledges financial support from National Science Foundation, National Institutes of Health (R01 GM52032; R24 GM069736) and U.S. Environmental Protection Agency, EPA (GAD R 832721-010). Although the research described in the article has been funded in part by the U.S. Environmental Protection Agency’s STAR program through grant (GAD R 832721-010), it has not been subjected to any EPA review and does not necessarily reflect the views of the Agency, and no official endorsement should be inferred.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.McAllister SR, Floudas CA. alpha-helical topology prediction and generation of distance restraints in membrane proteins. Biophys J. 2008;95:5281–5295. doi: 10.1529/biophysj.108.132241. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Fuchs A, Firschner A, Frishman D. Prediction of helix-helix contacts and interacting helices in polytopic membrane proteins using neural networks. Proteins. 2009;74:857–871. doi: 10.1002/prot.22194. [DOI] [PubMed] [Google Scholar]
- 3.Lo A, Chiu YY, Rødland EA, Lyu PC, Sung TY, Hsu WL. Predicting helix-helix interactions from residue contacts in membrane proteins. Bioinformatics. 2009;25:996–1003. doi: 10.1093/bioinformatics/btp114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Zhang Y. Progress and challenges in protein structure prediction. Current opinion in structural biology. 2008;18(3):342–348. doi: 10.1016/j.sbi.2008.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Floudas CA, Fung HK, McAllister SR, Monnigmann M, Rajgaria R. Advances in protein structure prediction and de novo protein design: A review. Chemical Engineering Science. 2006;61:966–988. [Google Scholar]
- 6.Kolodny R, Petrey D, Honig B. Protein structure comparison: implications for the nature of ‘fold space’, and structure and function prediction. Current opinion in structural biology. 2006;16(3):393–398. doi: 10.1016/j.sbi.2006.04.007. [DOI] [PubMed] [Google Scholar]
- 7.Floudas CA. Computational methods in protein structure prediction. Biotechnology and Bioengineering. 2007;97(2):207–213. doi: 10.1002/bit.21411. [DOI] [PubMed] [Google Scholar]
- 8.Ginalski K. Comparative modeling for protein structure prediction. Current opinion in structural biology. 2006;16(3):172–177. doi: 10.1016/j.sbi.2006.02.003. [DOI] [PubMed] [Google Scholar]
- 9.Cheng JL. A multi-template combination algorithm for protein comparative modeling. BMC Structural biology. 2008;8:18. doi: 10.1186/1472-6807-8-18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Petrey D, Honig B. Protein structure prediction: inroads to biology. Mol Cell. 2005;20(6):811–819. doi: 10.1016/j.molcel.2005.12.005. [DOI] [PubMed] [Google Scholar]
- 11.Dunbrack RL., Jr Sequence comparison and protein structure prediction. Curr Opin Struct Biol. 2006;16(3):374–84. doi: 10.1016/j.sbi.2006.05.006. [DOI] [PubMed] [Google Scholar]
- 12.Xu JB, Jiao F, Yu LB. Protein structure prediction using threading. Methods in molecular biology. 2008;413:91–121. doi: 10.1007/978-1-59745-574-9_4. [DOI] [PubMed] [Google Scholar]
- 13.Wu ST, Zhang Y. LOMETS: A local meta-threading-server for protein structure prediction. Nucleic Acids Research. 2007;35:3375–3382. doi: 10.1093/nar/gkm251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Przybylski D, Rost B. Improving fold recognition without folds. J Mol Biol. 2004;341(1):255–269. doi: 10.1016/j.jmb.2004.05.041. [DOI] [PubMed] [Google Scholar]
- 15.Wang G, Jin Y, Dunbrack RL., Jr Assessment of fold recognition predictions in CASP6. Proteins. 2005;61(7):46–66. doi: 10.1002/prot.20721. [DOI] [PubMed] [Google Scholar]
- 16.Rohl CA, Strauss CE, Chivian D, Baker D. Modeling structurally variable regions in homologous proteins with rosetta. Proteins. 2004;55(3):656–77. doi: 10.1002/prot.10629. [DOI] [PubMed] [Google Scholar]
- 17.Zhang Y, Kolinski A, Skolnick J. TOUCHSTONE II: a new approach to ab initio protein structure prediction. Biophys J. 2003;85(2):1145–64. doi: 10.1016/S0006-3495(03)74551-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Kolinski A. Protein modeling and structure prediction with a reduced representation. Acta Biochim Pol. 2004;51(2):349–371. [PubMed] [Google Scholar]
- 19.Floudas CA. Deterministic global optimization: theory, methods and applications Nonconvex optimization and its applications. Dordrecht, The Netherlands: Kluwer Academic Publishers; [Google Scholar]
- 20.Srinivasan R, Rose GD. Ab initio prediction of protein structure using LINUS. Proteins. 2002;47:489–495. doi: 10.1002/prot.10103. [DOI] [PubMed] [Google Scholar]
- 21.Klepeis JL, Wei YN, Hecht MH, Floudas CA. Ab initio prediction of the three-dimensional structure of a de novo designed protein: A double-blind case study. Proteins-structure function and bioinformatics. 2005;58:560–570. doi: 10.1002/prot.20338. [DOI] [PubMed] [Google Scholar]
- 22.Lee J, Pillardy J, Czaplewski C, Arnautova Y, Ripoll DR, Liwo A, Gibson KD, Wawak RJ, Scheraga HA. Efficient parallel algorithms in global optimization of potential energy functions for peptides, proteins, and crystals. Computer Physics Communications. 2000;128:399–411. [Google Scholar]
- 23.Klepeis JL, Floudas CA. ASTRO-FOLD: a combinatorial and global optimization framework for Ab initio prediction of three-dimensional structures of proteins from the amino acid sequence. Biophys J. 2003;85(4):2119–2146. doi: 10.1016/s0006-3495(03)74640-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Lacapére JJ, Pebay-Peyroula E, Neumann JM, Etchebest C. Determing membrane protein structures: still a challenge! Trends in biochemical sciences. 2007;32(6):259–70. doi: 10.1016/j.tibs.2007.04.001. [DOI] [PubMed] [Google Scholar]
- 25.Engel A, Gaub HE. Structure and mechanics of membrane proteins. Annual Review of Biochemistry. 2008;77:127–148. doi: 10.1146/annurev.biochem.77.062706.154450. [DOI] [PubMed] [Google Scholar]
- 26.Barth P, Wallner B, Baker D. Prediction of membrane protein structures with complex topologies using limited constraints. Proceedings of the National Academy of Sciences. 2009;106:1409–1414. doi: 10.1073/pnas.0808323106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Hopkins AL, Groom CR. The druggable genome. Nat Rev Drug Discov. 2002;1:727–730. doi: 10.1038/nrd892. [DOI] [PubMed] [Google Scholar]
- 28.Berman HM, Battistuz T, Bhat TN, Bluhm WF, Bourne PE, Burkhardt K, Feng Z, Gilliland GL, Iype L, Jain S, Fagan P, Marvin J, Padilla D, Ravichandran V, Schneider B, Thanki N, Weissig H, Westbrook JD, Zardecki C. The protein data bank. Acta Crystallogr D Biol Crystallogr. 2002;58:899–907. doi: 10.1107/s0907444902003451. [DOI] [PubMed] [Google Scholar]
- 29.Forrest LC, Tang CL, Honig B. On the accuracy of homology modeling and sequence alignment methods applied to membrane proteins. Biophys J. 2006;91(2):508–517. doi: 10.1529/biophysj.106.082313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Elofsson A, Heijne GV. Membrane protein structure: prediction versus reality. Annual Review of Biochemistry. 2007;76:125–140. doi: 10.1146/annurev.biochem.76.052705.163539. [DOI] [PubMed] [Google Scholar]
- 31.Hunte C, Richers S. Lipids and membrane protein structures. Current Opinion in Structural Biology. 2008;18:406–411. doi: 10.1016/j.sbi.2008.03.008. [DOI] [PubMed] [Google Scholar]
- 32.Yarov-Yarovoy V, Schonbrun J, Baker D. Multipass membrane protein structure prediction using Rosetta. Proteins. 2006;62(4):1010–25. doi: 10.1002/prot.20817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Zhang Y, DeVries ME, Skolnick J. Structure modeling of all identified G protein-coupled receptors in the Human Genome. PLoS Comput Biol. 2006;2(2):e13. doi: 10.1371/journal.pcbi.0020013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Fleishman SJ, Unger VM, Ben-Tal N. Transmembrane protein structures without X-rays. Trends Biochem Sci. 2006;31(2):106–13. doi: 10.1016/j.tibs.2005.12.005. [DOI] [PubMed] [Google Scholar]
- 35.Michino1 M, Chen J, Stevens RC, Brooks CL., III FoldGPCR: Structure prediction protocol for the transmembrane domain of G protein-coupled receptors from class A. 2010;78(10):21892201. doi: 10.1002/prot.22731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Gromiha MM, Selvaraj S. Inter-residue interactions in protein folding and stability. Prog Biophys Mol Biol. 2004;86(2):235–77. doi: 10.1016/j.pbiomolbio.2003.09.003. [DOI] [PubMed] [Google Scholar]
- 37.Tanaka S, Scheraga HA. Model of protein folding: inclusion of short-, medium-, and long-range interactions. Proc Natl Acad Sci. 1975;72(10):3802–6. doi: 10.1073/pnas.72.10.3802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Wako H, Scheraga HA. Use of distance constraints to fold a protein. Macromolecules. 1981;14:961–969. [Google Scholar]
- 39.McAllister SR, Mickus BE, Klepeis JL, Floudas CA. A novel approach for alpha-helical topology prediction in globular proteins: generation of interhelical restraints. Proteins. 2006;65:930–952. doi: 10.1002/prot.21095. [DOI] [PubMed] [Google Scholar]
- 40.Göbel U, Sander C, Schneider R, Valencia A. Correlated mutations and residue contacts in proteins. Proteins. 1994;18:309–317. doi: 10.1002/prot.340180402. [DOI] [PubMed] [Google Scholar]
- 41.Ortiz AR, Kolinski A, Rotkiewicz P, Ilkowski B, Skolnick J. Ab initio folding of proteins using restraints derived from evolutionary in formation. Proteins. 1999;37(S3):177–185. doi: 10.1002/(sici)1097-0134(1999)37:3+<177::aid-prot22>3.3.co;2-5. [DOI] [PubMed] [Google Scholar]
- 42.Rajgaria R, McAllister SR, Floudas CA. Towards accurate residue-residue hydrophobic contact prediction for alpha helical proteins via integer linear optimization. Proteins. 2009;74:929–947. doi: 10.1002/prot.22202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Rajgaria R, Wei Y, Floudas CA. Contact prediction for beta and alpha-beta proteins using integer linear optimization and its impact on the first principles 3d structure prediction method ASTRO-FOLD. Proteins. 2010;78:1825–1846. doi: 10.1002/prot.22696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Klepeis JL, Floudas CA. Prediction of beta-sheet topology and disulfide bridges in polypeptides. Journal of Computational Chemistry. 2003;24:191–208. doi: 10.1002/jcc.10167. [DOI] [PubMed] [Google Scholar]
- 45.Klepeis JL, Floudas CA. Ab initio tertiary structure prediction of proteins. J Global Optim. 2003;25:113140. [Google Scholar]
- 46.Klepeis JL, Pieja MT, Flouda CA. A new class of hybrid global optimization algorithms for peptide structure prediction: integrated hybrids. Comput Phys Commun. 2003;151:121140. [Google Scholar]
- 47.Klepeis JL, Pieja MT, Flouda CA. A new class of hybrid global optimization algorithms for peptide structure predic tion: alternating hybrids and application for met-enkephalin and melittin. Biophys J. 2003;84:869882. doi: 10.1016/S0006-3495(03)74905-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Klepeis JL, Floudas CA, Morikis D, Lambris JD. Predicting Peptide structures using NMR data and deterministic global optimization. Journal of Computational Chemistry. 1999;20(13):1354–1370. [Google Scholar]
- 49.Klepeis JL, Floudas CA. Free energy calculations for peptides via deterministic global optimization. Journal of Chemical Physics. 1999;110:7491–7512. [Google Scholar]
- 50.Cheng J, Baldi P. Improved residue contact prediction using support vector machines and a large feature set. BMC Bioinformatics. 2007;8:113–121. doi: 10.1186/1471-2105-8-113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Vicatos S, Kaznessis YN. Separating true positive predicted residue contacts from false positive ones in mainly alpha proteins, using constrained metropolis MC simulations. Proteins. 2008;70:539–552. doi: 10.1002/prot.21553. [DOI] [PubMed] [Google Scholar]
- 52.Shackelford G, Karplus K. Contact prediction using mutual information and neural nets. Proteins. 2007;69:159–164. doi: 10.1002/prot.21791. [DOI] [PubMed] [Google Scholar]
- 53.Punta M, Rost B. PROFcon: novel prediction of long-range contacts. Bioinformatics. 2005;21:2960–2968. doi: 10.1093/bioinformatics/bti454. [DOI] [PubMed] [Google Scholar]
- 54.Lund O, Frimand K, Gorodkin J, Bohr H, Bohr J, Hansen J, Brunak S. Protein distance constraints predicted by neural networks and probability density functions. Protein Eng. 1997;10:1241–1248. doi: 10.1093/protein/10.11.1241. [DOI] [PubMed] [Google Scholar]
- 55.Horner DS, Pirovano W, Pesole G. Correlated substitution analysis and the prediction of amino acid structural contacts. Briefings in Bioinformatics. 2008;9(1):46–56. doi: 10.1093/bib/bbm052. [DOI] [PubMed] [Google Scholar]
- 56.Fariselli P, Olmea O, Valencia A, Casadio R. Prediction of contact maps with neural networks and correlated mutations. Protein Engineering. 2001;14:835–843. doi: 10.1093/protein/14.11.835. [DOI] [PubMed] [Google Scholar]
- 57.Zhao Y, Karypis G. Prediction of contact maps using support vector machines. Proc of the IEEE Symposium on BioInformatics and BioEngineering. 2003:26–33. [Google Scholar]
- 58.Latek D, Kolinski A. Contact prediction in protein modeling: Scoring, folding and refinement of coarse-grained models. BMC Structural Biology. 2008;8:36. doi: 10.1186/1472-6807-8-36. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Nugent T, Jones DT. Predicting Transmembrane Helix Packing Arrangements using Residue Contacts and a Force-Directed Algorithm. PLoS Computational Biology. 2010;6(3):e1000714. doi: 10.1371/journal.pcbi.1000714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Jayasinghe S, Hristova K, White SH. MPTopo: A database of membrane protein topology. Protein Sci. 2001;10(2):455–458. doi: 10.1110/ps.43501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Raman P, Cherezov V, Caffrey M. The membrane protein data bank. Cell Mol Life Sci. 2006;63:36–51. doi: 10.1007/s00018-005-5350-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Tusnády GE, Dosztányi Z, Simon I. Transmembrane proteins in the Protein Data Bank: identification and classification. Bioinformatics. 2004;20(17):2964–2972. doi: 10.1093/bioinformatics/bth340. [DOI] [PubMed] [Google Scholar]
- 63.Adamian L, Liang J. Helix-helix packing and interfacial pairwise interactions of residues in membrane proteins. J Mol Biol. 2001;311(4):891–907. doi: 10.1006/jmbi.2001.4908. [DOI] [PubMed] [Google Scholar]
- 64.Adamian L, Jackups R, Binkowski TA, Liang J. Higher-order interhelical spatial interactions in membrane proteins. J Mol Biol. 2003;327:251–272. doi: 10.1016/s0022-2836(03)00041-x. [DOI] [PubMed] [Google Scholar]
- 65.Wang G, Dunbrack RL., Jr PISCES: a protein sequence culling server. Bioinformatics. 2003;19:1589–1591. doi: 10.1093/bioinformatics/btg224. [DOI] [PubMed] [Google Scholar]
- 66.Shindyalov IN, Bourne PE. Protein structure alignment by incremental combinatorial extension (CE) of the optimal path. Protein Engineering. 1999;11(9):739–747. doi: 10.1093/protein/11.9.739. [DOI] [PubMed] [Google Scholar]
- 67.http://blanco.biomol.uci.edu/mptopo/
- 68.McAllister SR, Mickus BE, Klepeis JL, Floudas CA. A novel approach for alpha-Helical topology prediction in globular proteins: generation of tnterhelical restraints. Proteins. 2006;65:930–952. doi: 10.1002/prot.21095. [DOI] [PubMed] [Google Scholar]
- 69.Floudas CA. Nonlinear and Mixed-Integer Optimization: Fundamentals and Applications. Oxford University Press; 1995. [Google Scholar]
- 70.Graña O, Baker D, MacCallum RM, Meiler J, Punta M, Rost B, Tress ML, Valencia A. CASP6 assessment of contact prediction. Proteins. 2005;61(7):214–24. doi: 10.1002/prot.20739. [DOI] [PubMed] [Google Scholar]
- 71.Miyazawa S, Jernigan RL. Estimation of effective interresidue contact energies from protein crystal structures: quasi-chemical approximation. Macromolecules. 1985;18(3):534–552. [Google Scholar]
- 72.Schobert B, Cupp-Vickery J, Hornak V, Smith SO, Lanyi JK. Crystallographic structure of the K intermediate of bacteriorhodopsin: conservation of free energy after photoisomerization of the retinal. Journal of Molecular Biology. 2002;321:715–726. doi: 10.1016/s0022-2836(02)00681-2. [DOI] [PubMed] [Google Scholar]
- 73.Lieberman RL, Rosenzweig AC. Crystal structure of a membrane-bound metalloenzyme that catalyses the biological oxidation of methane. Nature. 2005;434:177–182. doi: 10.1038/nature03311. [DOI] [PubMed] [Google Scholar]
- 74.Gordeliy VI, Labahn J, Moukhametzianov R, Efremov R, Granzin J, Schlesinger R, Bueldt G, Savopol T, Scheidig A, Klare JP, Engelhard M. Molecular basis of transmembrane signalling by sensory Rhodopsin II-transducer complex. Nature. 2002;419:484–487. doi: 10.1038/nature01109. [DOI] [PubMed] [Google Scholar]
- 75.Palczewski K, Kumasaka T, Hori T, Behnke CA, Motoshima H, Fox BA, Trong IL, Teller DC, Okada T, Stenkamp RE, Yamamoto M, Miyano M. Crystal structure of rhodopsin: A G protein-coupled receptor. Science. 2000;289:739–745. doi: 10.1126/science.289.5480.739. [DOI] [PubMed] [Google Scholar]
- 76.Jaakola VP, Griffith MT, Hanson MA, Cherezov V, Chien EY, Lane JR, Ijzerman AP, Stevens RC. The 2.6 Angstrom crystal structure of a human A2A adenosine receptor bound to an antagonist. Science. 2008;322:1211–1217. doi: 10.1126/science.1164772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Jones DT. Improving the accuracy of transmembrane protein topology prediction using evolutionary information. Bioinformatics. 2007;23(5):538–544. doi: 10.1093/bioinformatics/btl677. [DOI] [PubMed] [Google Scholar]
- 78.Abe K, Tani K, Nishizawa T, Fujiyoshi Y. Inter-subunit interaction of gastric H+, K+-ATPase prevents reverse reaction of the transport cycle. EMBO J. 2009 Jun 3;28(11):1637–43. doi: 10.1038/emboj.2009.102. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


