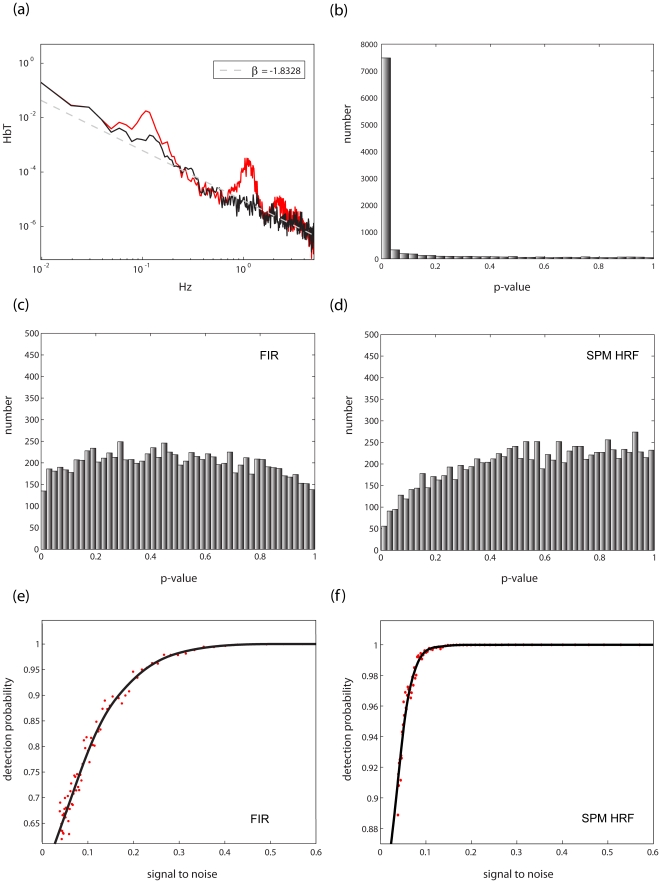
Figure 1. Noise characteristics of NIRS DATA.
(a): A representative power spectrum of a NIRS time series captured in the absence of stimulation (rest data in red) displayed on a logarithmic scale. The power spectrum follows a power law (exponent ∼ −1.8) tightly, apart from conspicuous deviations caused by systemic artifacts. The spectrum of the same time series after artifact reduction (see Methods section 2.1) is plotted in black. (b) Data were simulated data to mimick NIRS rest data (exponent −2). Ten thousand random vectors of this type were generated and analyzed with a GLM representing the design of the task described in Methods section 1, applying the precoloring method [23] to subdue autocorrelation. Next an ANOVA (for the FIR model) or a t-test (for the SPM-HRF model) wass carried out on the resulting coefficients, and the significance (p-value) for each derived. The resulting histogram of p-values is shown (c) A similar set of simulated noise was fitted with a FIR model representing the task design, and the FGLS (feasible generalized least squares- i.e. whitening according to a power law fit + precoloring (0.017 Hz)) method described in Methods section 2.3 was applied. The resulting histogram of p-values is very close to the theoretical optimum. (d) Simulated noise was fitted with a single basis function – the SPM hemodynamic response function [9] and the FGLS method described in Methods section 2.3 was applied. The resulting histogram of p-values exhibits some slight negative bias. (e-f) The same design vector was convolved with the SPM HRF. It then served as a model signal to which simulated noise of varying degrees was added. Next, FGLS was carried out using both the FIR and SPM HRF model. Probability of detection (average p-value) as a function of signal to noise (ratio of RMS (root means squared) squared) for the FIR (e) and SPM HRF model (f) are shown. As can be seen, both models are highly sensitive in the face of noise although, unsurprisingly, given that in the case of the SPM HRF model the model and signal are identical, the SPM HRF model is more sensitive in this case.