Abstract
Motivation: RNA secondary structure plays an important role in the function of many RNAs, and structural features are often key to their interaction with other cellular components. Thus, there has been considerable interest in the prediction of secondary structures for RNA families. In this article, we present a new global structural alignment algorithm, RNAG, to predict consensus secondary structures for unaligned sequences. It uses a blocked Gibbs sampling algorithm, which has a theoretical advantage in convergence time. This algorithm iteratively samples from the conditional probability distributions P(Structure | Alignment) and P(Alignment | Structure). Not surprisingly, there is considerable uncertainly in the high-dimensional space of this difficult problem, which has so far received limited attention in this field. We show how the samples drawn from this algorithm can be used to more fully characterize the posterior space and to assess the uncertainty of predictions.
Results: Our analysis of three publically available datasets showed a substantial improvement in RNA structure prediction by RNAG over extant prediction methods. Additionally, our analysis of 17 RNA families showed that the RNAG sampled structures were generally compact around their ensemble centroids, and at least 11 families had at least two well-separated clusters of predicted structures. In general, the distance between a reference structure and our predicted structure was large relative to the variation among structures within an ensemble.
Availability: The Perl implementation of the RNAG algorithm and the data necessary to reproduce the results described in Sections 3.1 and 3.2 are available at http://ccmbweb.ccv.brown.edu/rnag.html
Contact: charles_lawrence@brown.edu
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
RNA secondary structure plays a key role in the function of many types of RNA, including structural RNAs, non-coding RNAs (ncRNA) and regulatory motifs in mRNAs (e.g. riboswitches). Accordingly, structural features of RNA molecules are often characterized by evolutionarily conserved secondary structures that are critical to their functions. Furthermore, there are often multiple occurrences of these structural elements within one species (e.g. tRNA). Given the recent recognition of many important additional roles that RNAs play in cellular functions, predicting the common structural features of a set of RNA sequences is more important than ever.
1.1 Structure prediction for a single sequence
Three main classes of probabilistic models of P(S|Q) for the prediction of the secondary structure (S) for a single sequence (Q), are currently available. The most popular is a thermodynamic model that supposes that RNA structures may be described by Boltzmann statistics [e.g. Mfold (Zuker et al., 1981)]. The second model incorporates phylogenetic information into folding [e.g. PETfold (Seemann et al., 2008)]. The third method abandons the biophysical model in favor of machine learning algorithms that empirically infer structure based on probabilistic graphical models [e.g. CONTRAfold (Do et al., 2006)] or non-parametric methods [e.g. KNETfold (Bindewald et al., 2006)].
Algorithms that use a thermodynamic model have gained wide acceptance, particularly the early algorithms like Mfold (Zuker et al., 1981) and RNAfold (Hofacker et al., 1994) that use dynamic programming to find the most probable structure (MPS), i.e. the ‘minimum free energy structure’ (MFE). However, the Boltzmann weighted ensemble of structures, represented as a large set of binary matrices, defines a high-dimensional discrete space in which even the MPS is likely to have low probability. Furthermore, the MPS is often not representative of the Boltzmann weighted ensemble of structures. In particular, there is no fundamental reason for the MPS to even be included in the high-weight region of the Boltzmann space (Carvalho et al., 2008). Thus, alternative estimators that gain information from the full ensemble of structures have emerged, including centroid estimators (Carvalho et al., 2008; Ding et al., 2005) and the related maximum expected accuracy (MEA) estimator (Do et al., 2006). A generalization of the centroid estimator, the γ -centroid (Hamada et al., 2009, 2011), permits the balancing of false positive and false negative errors based on the tunable parameter γ. Moreover, the focus on finding the MPS without uncertainty analysis implicitly assumes that an RNA molecule exists only in one single stable state, which is not the case for many RNAs, and almost certainly is not the case for mRNAs. To address these issues, sampling algorithms like Sfold (Ding et al., 2005) provide a method to characterize the full ensemble of structures (Mathews, 2006), and Bayesian confidence limits, a.k.a. credibility limits, provide a method to delineate the uncertainty of an estimate (Newberg et al., 2009; Webb et al., 2008).
1.2 Structure prediction for multiple unaligned sequences
With multiple sequences, the problem becomes harder since the extra unknown alignment (A) of the sequences enters and the model becomes P(S,A|Q). Algorithms that address the two major components of this problem, i.e. the prediction of common structure given an alignment and predicting an alignment given a common structure, have been developed. The first of these assumes an alignment of sequences is given, and seeks to predict the structure common to the aligned sequences, i.e. draw inference from P(S|A,Q). Several methods have been developed for this problem. Mutual information (Gutell et al., 1992) and stochastic context-free grammars (SCFG) (Knudsen et al., 1999; Sakakibara et al., 1994) have been effectively used to detect and model complementary covariation that is indicative of conserved base pairing interactions. Maximum weighted matching (MWM), a graph-theoretical approach, was introduced to predict common secondary structures allowing pseudoknots (Cary et al., 1995; Tabaska et al., 1998). RNAalifold (Bernhart et al., 2008; Hofacker et al., 2002) incorporates both thermodynamic parameters and sequence covariation, and permits sampling of consensus structures from its probabilistic model.
Algorithms for finding a multiple alignment given a common structure, i.e. P(A|S,Q), have also been developed. There are well-known generic multiple alignment algorithms, e.g. ClustalW2 (Chenna et al., 2003) and ProbCons (Do et al., 2005), but these do not incorporate structural information, and thus model only P(A|Q). Of more direct interest here are algorithms that use a given consensus structure to predict a multiple alignment, i.e. the model P(A|S,Q). Such methods can improve the alignment of RNA sequences (Nawrocki and Eddy, 2007). In one approach, structures of individual sequences are predicted separately and abstractions of these structures aligned (Giegerich et al., 2004; Siebert et al., 2005; Steffen et al., 2006). Another approach (Ji et al., 2004) applies graph theory to find stems conserved across multiple sequences first, and then assembles conserved stem blocks to form consensus structures in which pseudoknots are permitted. The probabilistic covariance model (Eddy and Durbin, 1994) employs the SCFG model to multiply align sequences using a given consensus structure. This algorithm iterates between parameter estimation and alignment prediction using an expectation maximization (EM) algorithm. After convergence, it permits sampling of alignments. Eddy and Durbin (1994) also presented an iterative optimization procedure that iterates between alignment and structure, taking an optimization approach instead of the sampling approach we describe here. More recently, Yao et al. (2006) described CMfinder, an extension of this approach to find regulatory motifs.
There is a ‘chicken and egg’ problem for these two classes of algorithms: a good RNA sequence alignment (A) depends on a specified consensus structure (S), and a good consensus structure (S) prediction depends on a good alignment (A). One approach to solving this dilemma is to simultaneously align and fold a pair of RNA sequences with a dynamic programming algorithm (Sankoff, 1985). However, the computational complexity is O(n6), too high to be of practical value in all but very short sequences. Heuristics based on simplifications and restrictions of the Sankoff algorithm for multiple sequences (more than two) have been developed, such as FoldalignM (Torarinsson et al., 2007), mLocARNA (Will et al., 2007), Murlet (Kiryu et al., 2007a) and RNA Alignment and Folding (RAF) (Do et al., 2008).
Another approach is to iteratively predict structure and alignment conditioned on each other. Early work focused on finding the optimal solution with an EM algorithm (Eddy et al., 1994; Yao et al., 2006) or simulated annealing (Lindgreen et al., 2007). Recently, approaches that draw samples from probabilistic models using Markov chain Monte Carlo (MCMC) procedures have been described. Meyer et al. (2007) employs a Metropolis–Hastings algorithm that makes proposals for local alignment and structure changes, accepting them probabilistically. However, the slow convergence of these local-move algorithms tends to require a large number of sampling steps. Another variation is RNAsampler (Xing et al., 2007), which heuristically iterates between the alignment and sampling of candidate stems in the multiple sequences.
Gibbs sampling, introduced by Geman and Geman (1984), is another popular MCMC procedure. Inspired by a theorem of Liu (1994) concerning accelerated convergence of various Gibbs samplers, here we describe a blocked sampling algorithm that iterates between alignment (A) and structure prediction (S). In Liu's first theorem, three alternative Gibbs sampling approaches are considered: (i) the standard Gibbs sampler in which each of the random variables (RVs) are sampled individually; (ii) the grouped Gibbs sampler in which two or more of the RVs are sampled jointly in blocks; and (iii) the collapsed Gibbs sampler in which at least one of the RVs is removed from the problem via integration. He compares their convergence rates based on their forward operators, Fs, Fg, Fc. The theorem shows that the norms of these operators are ordered as follows: ||Fc||≤||Fg||≤||Fs||. Thus, the expected number of iterations until convergence follows the reverse order. However, as he points out, if the computation required at each iteration to sample blocks or to remove RVs via integration is too large, then any improvements in convergence rate may not be worth the added computational expense. Thus, the key is to find efficient procedures for blocking or integrating.
Here we describe a Gibbs sampling algorithm that capitalizes on Liu's theorem via block sampling. This algorithm, which we call RNAG, iteratively block samples from the conditional probability distributions P(Structure | Alignment) and P(Alignment | Structure), and in so doing refines the models of both Alignment and Structure. We use these samples to characterize the shape of the posterior space using hierarchal clustering and centroid estimators. We use γ -centroid estimators to delineate the trade-off between the positive predictive value (PPV) and the sensitivity of the algorithm, and credibility limits to characterize the uncertainty of our predictions.
2 METHODS
2.1 RNAG sampling algorithm
Consider the probabilistic model P(A,S|ΛA,ΛS,Q) for multiple sequences Q, where the hidden variables are A (the alignment) and S (the consensus structure), and ΛA, ΛS are the corresponding parameters of the A, S prediction steps. The goal is to find samples from the joint distribution P(A,S|ΛA, ΛS,Q). RNAG, the blocked Gibbs sampler described here, achieves this by iteratively sampling from the conditional probabilities P(S(t)|A(t−1), ΛS,Q) and P(A(t)|S(t−1), ΛA,Q), at the t-th iteration. Notice that our algorithm provides a generic framework that can employ any probabilistic sampling algorithms in each of its two sampling steps. Specifically, RNAG proceeds as follows.
2.1.1 Alignment initialization
In theory, it does not matter if the algorithm starts from an initial alignment or an initial consensus structure. Here, we begin with an initial alignment A(0) produced by ProbCons (Do et al., 2005) under the model P(A|Q).
2.1.2 Iteration steps
Sample a consensus structure (S(t)) given an alignment (A(t−1)). To sample from P(S(t)|A(t−1), ΛS,Q), we employ RNAalifold (Bernhart et al., 2008), which combines thermodynamic parameters and empirical parameters estimated from the aligned sequences using a default covariation weight ΛS.
Sample an alignment (A(t)) given a consensus structure (S(t)). To sample from P(A(t)|S(t), ΛA,Q), we employ the Infernal package (Nawrocki et al., 2009). ΛA is a set of empirical parameter estimates (parameters for SCFG model) obtained from P(ΛA|S(t), A(t − 1), Q) using an EM algorithm. Given ΛA, a multiple alignment is sampled from P(A(t)| ΛA, S(t) ,Q) using the SCFG model.
Supplementary Figure S1 shows a diagram of these steps.
2.2 Sample analysis: characterization of the posterior space
As described by Mathews (2006), sampling from the Boltzmann weighted ensemble of secondary structures can provide a full characterization of this structure space. Here, the RNAG sampler draws samples from the very high-dimensional space of structures and alignments. In our approach, attention is focused on the sampled structures, though the multiple alignments also evolve during the sampling. We employed clustering analysis to characterize the overall shape of the posterior space of structures, and credibility limits to delineate uncertainty in predicted structures.
2.2.1 Clustering analysis
Boltzmann weighted ensembles of RNA secondary structures can exhibit complex shapes, which often include multiple modes (Ding et al., 2006). Here we examine the shape of the probabilistically weighted posterior space using a hierarchical clustering procedure like that employed by Ding et al. (2006) for a single sequence.
Direct comparison of the sampled consensus structures is impractical because of the dependence of the indices of the bases of sampled structures on the alignment. Thus, we followed the second evaluation procedure described by Hamada et al. (2011), projecting the consensus structure back onto each sequence, and then used a hierarchical clustering method on the projected structures.
2.2.2 Centroid estimator
We calculated γ -centroid estimators (Hamada et al., 2009) for structure prediction and for comparison with alternative prediction methods. Specifically, we used estimates of marginal probabilities of base pairs obtained from base pair frequencies from the Gibbs sampler after a burn-in period to obtain the γ-centroid estimators. For each RNAG experiment described in Section 3, we sampled a burn-in period of 1000 iterations, and used the next 1000 sampled structures for clustering and calculation of the centroid. The γ-centroid, as a generalization of the centroid estimator, provides a means to balance sensitivity and PPV and accordingly can be used to compare procedures over the range of this trade-off. We employed the γ-centroid estimator for such comparisons and the original centroid estimator in calculations of bias and variance.
2.3 Evaluation metric
2.3.1 Prediction accuracy
To evaluate prediction accuracy, we compared the predicted structure for each sequence with its reference structure and calculated sensitivity (SEN) and PPV. SEN is the fraction of known base pairs correctly predicted, and PPV is the fraction of predicted base pairs that are in the known structure (Mathews, 2004). Using γ-centroid estimation, we can interpolate a curve on the PPV-−SEN plane based on different γ values (Hamada et al., 2011). Following the lead of Do et al. (2008), we report the average of (PPV, SEN) calculated for each test case, weighing each sequence equally. For the comparison of the relative performance of RNAG across RNA families, we used the area under the curve, acquired with linear interpolation, as a qualitative measure.
2.3.2 Uncertainty analysis
Credibility limits: Any prediction of structure provides only a point estimate of secondary structure, giving no information about the uncertainty of that estimate. We employed Bayesian confidence limits, a.k.a. credibility limits, to characterize this uncertainty (Newberg et al., 2009; Webb-Robertson et al., 2008). These limits compute the radius of the smallest hypersphere centered at the estimate containing 95% of the posterior weighted space.
Bias-variance analysis: In any prediction based on finite data involving comparison with a reference, deviations from the reference involve two components, bias and variance, where the bias measures the distance between the mean and the reference, and the variance gives the variation around the mean. In this discrete setting, where the secondary structure is treated as a binary matrix with random elements, the mean is almost certainly not a feasible RNA secondary structure, because it will almost certainly not be integer valued. Accordingly, here we measured bias as the distance between the reference structure and the structure in the ensemble that is nearest to the mean in the least squares sense (the centroid) (Carvalho and Lawrence, 2008), and the variance as the variation around the centroid of the ensemble. As Carvalho and Lawrence (2008) have shown, for binary variables, square error distances, p-th power error differences and Hamming distances are equal; thus, we used Hamming distances to calculate bias.
- Separation index: To assess how well separated the clusters of secondary structures were relative to the variation within clusters, we used the following separation index:
where D is the Hamming distance between the centroids of the two largest clusters, i.e. the total number of paired bases contained in one centroid structure but not the other, and C1, C2 are the 95% credibility limits around the two largest cluster centroids. When this index is at least 1, no more than 5% of the structures from either cluster are within the 95% credibility limit of the other cluster, and thus we say the two largest clusters are well separated.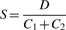
(1)
3 RESULTS
Following Hamada et al. (2011), we picked 17 γ-centroid estimators, where γ∈{2k: −5≤k≤10, k∈Z}∪{6} from which to interpolate the curve on the PPV–SEN plane.
3.1 Training
Because there are only a few current algorithms for each step of RNAG, and because we used default parameters and settings for each algorithm employed in our study, training in this study was very limited. Furthermore, since there are very few available algorithms that draw samples, we have explored only RNAalifold and Infernal for the two iteration steps. Using the dataset of Kiryu et al. (2007a), we compared ClustalW and ProbCons for the initialization step, and found that ProbCons returned better results; thus, the results presented here all use ProbCons.
3.2 Comparison of accuracy (testing)
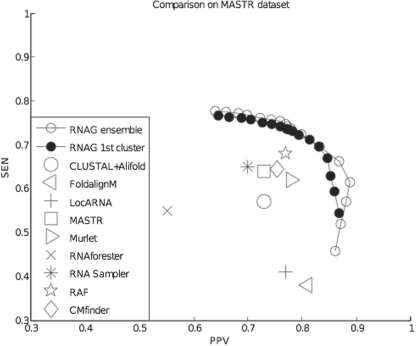
In our first accuracy assessment, we evaluated RNAG on the benchmark dataset from Lindgreen et al. (2007), herein called the MASTR dataset. Structure prediction results from current algorithms for this dataset are given in Do et al. (2008) and plotted together with the PPV-SEN curve from RNAG in Figure 1.
Fig. 1.
Average performance of different secondary structure prediction methods in the PPV–SEN plane for the MASTR dataset (Lindgreen et al., 2007). PPV = TP/P = TP/(TP + FP), SEN = TP/T = TP/(TP + FN). Note: the axis ranges are set from 0.3 to 1.0 to improve readability. Points showing the performance of extant procedures were taken from Do et al. (2008) except for CMfinder, which was included because of its similarity to RNAG. CMfinder was run at default values and settings.
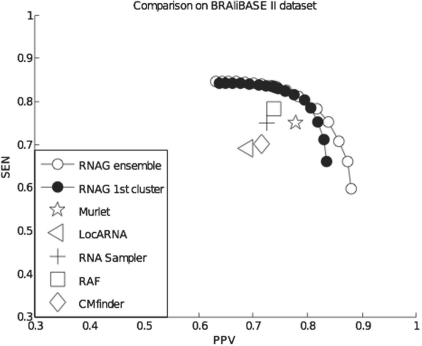
We also tested and compared different align-fold algorithms on the BRAliBASE II dataset (Gardner et al., 2005), which contains collections of ~100 five-sequence subalignments, sampled from four specific Rfam families (5S rRNA, group II intron, tRNA and U5 spliceosomal RNA) for which the BRAliBASE II dataset included reference alignments. For comparison, the results reported in Do et al. (2008) were averaged over the four RNA families and are shown plotted on the PPV–SEN plane along with the RNAG frontier in Figure 2.
Fig. 2.
Average performance of different secondary structure prediction methods in the PPV–SEN plane for four RNA families (5S rRNA, group II intron, tRNA and U5 spliceosomal RNA) from the BRAliBASE II dataset (Gardner et al., 2005). Note: the axis ranges are set from 0.3 to 1.0 to improve readability. Points showing the performance of extant procedures were taken from Do et al. (2008) except for CMfinder, which was run at defaults.
These comparisons demonstrate that the results of extant procedures lie below the RNAG frontier, indicating that, on average, RNAG provides a better trade-off between PPV and sensitivity. Not surprisingly, this is not always the case. Do et al. (2008) presents the results of prediction methods for each of the four RNA families in the BRAliBASE II dataset. Supplementary Figure S2 shows that 14 of these 16 predictions are below the RNAG frontier and 2 are somewhat above this frontier.
3.3 RNAG performance characteristics
We explored RNAG's properties using the benchmark dataset described by Kiryu et al. (2007a), which contains 85 reference alignments of 10 sequences each, representing 17 RNA families from the Rfam database (Griffiths-Jones et al., 2005). This dataset spans a range of sequence lengths from 51 to 291 bases, and a range of sequence identity from 40% to 94%, including nine families with identities under 60%. Kiryu et al. (2007a) used this dataset to compare algorithms that predict a consensus structure for an aligned set of sequences. Perhaps not surprisingly, as shown in Supplementary Figure S3, RNAG also outperforms these procedures, including CentroidAlifold (Hamada et al., 2011), a state-of-the-art algorithm. However, our purpose in using this dataset was to characterize the variation in RNAG performance with number of sequences in the alignment and over various RNA families.
3.3.1 Variation with the number of unaligned sequences
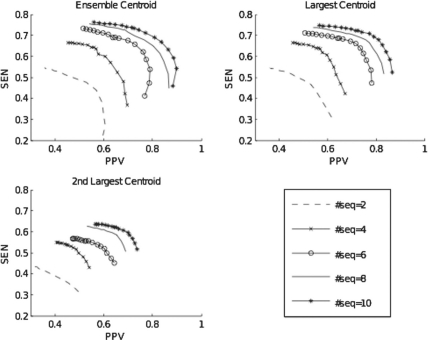
To assess the effect that the number of input sequences has on prediction accuracy, we took N (2≤N≤10) random sequences from each of the 85 reference alignments, ran RNAG on these subsets of sequences and averaged over 10 independent runs (except for N=10). The results are given in Table 1 and a subset of these results are shown as PPV–SEN curves in Figure 3, which shows that with additional sequences the structure prediction improves, but with decreasing increments, as indicated by the small improvement between 8 and 10 input sequences. However, Supplementary Figure S4 and Table S1 show that this finding differs between sequence sets, and depends on the average pairwise identity of the input sequences, suggesting that larger gains are attainable with additional sequences when the input sequences have <60% average pairwise identity. Notice in Table 1 that the bias decreases with the number of sequences in the alignment, but with decreasing gains, which is in agreement with improvements in the area under the PPV–SEN curves.
Table 1.
Effects of the number of sequences on prediction results
| No. of sequences | Area under PPV–SEN curve |
Bias | SD | No. of samples |
95% credibility limit |
||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Ensemble | First cluster | Second cluster | First cluster | Second cluster | First+second cluster | Ensemble | First cluster | Second cluster | |||
| 2 | 0.44 | 0.46 | 0.37 | 0.27 | 0.04 | 728.13 | 150.76 | 878.89 | 0.21 | 0.14 | 0.11 |
| 3 | 0.58 | 0.59 | 0.49 | 0.20 | 0.03 | 793.15 | 124.94 | 918.09 | 0.14 | 0.10 | 0.07 |
| 4 | 0.58 | 0.58 | 0.48 | 0.20 | 0.03 | 791.66 | 115.00 | 906.66 | 0.14 | 0.09 | 0.06 |
| 5 | 0.62 | 0.63 | 0.51 | 0.17 | 0.03 | 802.20 | 113.24 | 915.44 | 0.12 | 0.08 | 0.05 |
| 6 | 0.67 | 0.67 | 0.54 | 0.16 | 0.03 | 800.50 | 111.66 | 912.16 | 0.11 | 0.07 | 0.05 |
| 7 | 0.70 | 0.69 | 0.57 | 0.15 | 0.03 | 795.52 | 111.92 | 907.44 | 0.10 | 0.07 | 0.05 |
| 8 | 0.73 | 0.71 | 0.60 | 0.15 | 0.03 | 797.56 | 116.19 | 913.75 | 0.10 | 0.07 | 0.04 |
| 9 | 0.73 | 0.73 | 0.60 | 0.14 | 0.02 | 790.59 | 122.38 | 912.97 | 0.09 | 0.06 | 0.04 |
| 10 | 0.75 | 0.74 | 0.63 | 0.13 | 0.02 | 792.85 | 125.11 | 917.96 | 0.09 | 0.06 | 0.04 |
For each row, we not only calculate the average area under the PPV–SEN curve for accuracy comparison, but also summarize the bias-variance statistics and the size of the two biggest clusters to visualize the clustering results. In order to normalize bias, SD and credibility limits with respect to the sequence length, we divide them by the average sequence length for the family.
Fig. 3.
Improvement of the RNAG PPV–SEN curves with increasing numbers of input sequences.
3.3.2 A detailed look into each family
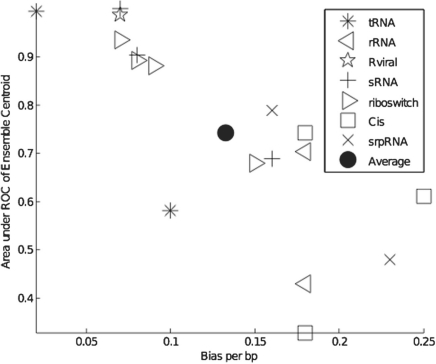
The above results describe the overall performance of RNAG for this dataset, but do not reveal differences across the families. In Table 2, we list the bias-variance statistics, area under the PPV–SEN curve and cluster statistics for each family. As this table indicates, there is considerable variability in the biases and under-curve areas, which reflects the fact that the ability to predict the reference structure varies widely between families. Figure 4 highlights this variability and shows a strong correlation between bias and the area under the PPV–SEN curve.
Table 2.
A detailed look into the RNAG results on 17 RNA families, listed in groups by their functional type
| RNA family | RNA type | Mean length (percent identity) | Bias | SD | 95% credibility limit |
PPV–SEN area |
No. of samples |
Separation index | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ensemble | First cluster | Second cluster | Ensemble | First cluster | Second cluster | First+second | First cluster | Second cluster | ||||||
| T-box | tRNA | 244 (45) | 0.10 | 0.01 | 0.06 | 0.04 | 0.02 | 0.58 | 0.55 | 0.47 | 926 | 826 | 100 | 1.00 |
| t-RNA | tRNA | 73 (45) | 0.02 | 0.01 | 0.03 | 0.01 | 0.01 | 1.00 | 0.99 | 0.91 | 949 | 888 | 61 | 2.50 |
| 5S-rRNA | rRNA | 116 (57) | 0.17 | 0.02 | 0.07 | 0.05 | 0.03 | 0.70 | 0.70 | 0.67 | 922 | 751 | 171 | 0.88 |
| 5-8S-rRNA | rRNA | 154 (61) | 0.18 | 0.03 | 0.14 | 0.10 | 0.08 | 0.43 | 0.42 | 0.26 | 907 | 744 | 163 | 0.56 |
| Retroviral-psi | Rviral | 117 (92) | 0.07 | 0.05 | 0.15 | 0.11 | 0.05 | 0.99 | 0.99 | 0.47 | 981 | 952 | 29 | 1.25 |
| U1 | sRNA | 157 (59) | 0.16 | 0.02 | 0.06 | 0.06 | 0.02 | 0.69 | 0.69 | 0.63 | 988 | 928 | 60 | 1.13 |
| U2 | sRNA | 182 (62) | 0.08 | 0.02 | 0.05 | 0.05 | 0.02 | 0.90 | 0.90 | 0.71 | 981 | 941 | 40 | 1.14 |
| Sno-14q-I-II | sRNA | 75 (64) | 0.07 | 0.03 | 0.12 | 0.08 | 0.07 | 1.00 | 0.92 | 0.86 | 838 | 636 | 202 | 0.47 |
| Lysine | riboswitch | 181 (49) | 0.07 | 0.02 | 0.06 | 0.05 | 0.03 | 0.94 | 0.93 | 0.84 | 983 | 923 | 60 | 0.88 |
| RFN | riboswitch | 140 (66) | 0.15 | 0.03 | 0.11 | 0.06 | 0.06 | 0.68 | 0.64 | 0.60 | 820 | 574 | 246 | 0.58 |
| THI | riboswitch | 105 (55) | 0.08 | 0.02 | 0.07 | 0.06 | 0.02 | 0.89 | 0.88 | 0.75 | 968 | 869 | 99 | 1.13 |
| S-box | riboswitch | 107 (66) | 0.09 | 0.02 | 0.07 | 0.03 | 0.03 | 0.88 | 0.87 | 0.74 | 945 | 806 | 139 | 1.17 |
| IRES-HCV | Cis | 261 (94) | 0.25 | 0.05 | 0.21 | 0.16 | 0.08 | 0.61 | 0.58 | 0.44 | 936 | 877 | 59 | 1.00 |
| SECIS | Cis | 64 (41) | 0.17 | 0.02 | 0.08 | 0.02 | 0.02 | 0.74 | 0.71 | 0.72 | 840 | 679 | 161 | 1.50 |
| UnaL2 | Cis | 54 (73) | 0.18 | 0.03 | 0.06 | 0.02 | 0.02 | 0.33 | 0.62 | 0.61 | 867 | 752 | 115 | 1.00 |
| SRP-bact | srpRNA | 93 (47) | 0.16 | 0.03 | 0.12 | 0.04 | 0.04 | 0.79 | 0.78 | 0.70 | 834 | 646 | 188 | 2.75 |
| SRP-euk-arch | srpRNA | 291 (40) | 0.23 | 0.01 | 0.04 | 0.03 | 0.02 | 0.49 | 0.48 | 0.47 | 921 | 837 | 84 | 0.80 |
| Average | 142 | 0.13 | 0.02 | 0.09 | 0.06 | 0.04 | 0.76 | 0.74 | 0.63 | 926 | 826 | 100 | 0.90 | |
We calculated the average area under the PPV–SEN curve for accuracy comparison, as well as statistics like bias, SD, credibility limit, and separation index from cluster analysis, to better understand the posterior secondary structure space.
Fig. 4.
2D plot of bias per base pair and the area under the PPV–SEN curve of the ensemble centroid for the 17 RNA families in Table 2. The results for each family are represented by a symbol indicating their functional group.
Furthermore, we observed that the normalized 95% credibility limits for the ensemble centroid are <10% for 11 of the families, which indicates that the probabilistically weighted ensembles are quite tightly compact around the centroid of the full ensemble for the majority of the families. Normalization was obtained by dividing the Hamming distances by the lengths of the sequences. In spite of this, 11 families have a separation index of at least 1 (shown in the last column of Table 2), indicating that the cluster centroids are well separated for these 11 families. Finally, notice that the biases, which give the distances between the predicted structures and the reference structures, are more than twice as large as the SDs of the distances of ensemble members around the predicted structures, which shows that the predictions are substantially more precise than they are accurate.
4 DISCUSSION
Our results comparing RNAG predictions to those from several additional recently published methods show that the existing procedures yield a combination of sensitivity and PPV that is considerably below the RNAG frontier. Some features of RNAG suggest an explanation for this behavior. RNAG not only inherits the advantages of the sampling method, but also enjoys a theoretical convergence advantage over the Metropolis–Hastings algorithm, which employs local moves. Since RNAG samples full, valid secondary structures, it enjoys an advantage over iterative algorithms that sample only stems. Also, since the two recursive steps sample from the full space of alignments and structures directly, we avoid the need to use a reduced model; a concession that is common to several extant procedures. However, since RNAG is an MCMC procedure, there are no means to assure that it has converged to its target distribution.
4.1 Limitations of comparison datasets and training
We specifically selected three published datasets and compared RNAG's performance to the published performance of other methods in order to avoid self-serving selection biases and biases that can arise with less than ideal application of extant methods. We added CMfinder to these comparisons by first reproducing the results in Yao et al. (2006) with default settings and then applying the published algorithm to the three datasets in this study with default settings. CMfinder was included because it is similar to RNAG, and as shown by Yao et al. (2006), it can be used to predict global RNA secondary structure, but in fairness, note that CMfinder was not designed primarily for this purpose. Of the three datasets, the most extensive is that of Kiryu et al. (2007a), which includes 17 Rfam families. We accept that in this field it is almost always difficult or impossible to obtain a truly representative dataset. Nevertheless, it is important to recognize that available datasets have limitations. Specifically, generalizations from these 17 families, plus the datasets from the other two comparison groups to the population of RNAs, should be drawn with some caution as the combined sample size is not large and these sets are not random samples. As pointed out above, we did very little to train RNAG in this implementation.
4.2 Potential improvement of RNAG
There are several potential means for improving RNAG. Since we have done no training to select options or parameters for the algorithmic components in this implementation, the performance of RNAG could potentially be improved by exploiting the full strength of these packages and by tuning the model on a training set. Moreover, RNAG is only a framework for computation and the auxiliary packages above can be replaced by any other algorithms that are designed for P(A|Q), P(S|A,Q) and P(A|S,Q). Furthermore, RNAG now takes the theoretical advantage of a blocked Gibbs sampler by grouping parameters to sample into S and A. A further increase in the convergence rate may be available by integrating out A from the model to take advantage of the collapsed Gibbs sampler. There are several other options for improving the algorithm's speed, including the use of better stopping rules, parallel implementation, and the use of more advanced sampling methods such as parallel tempering.
4.3 An alternative goal of these algorithms
Our finding of substantial biases in the Kiryu et al. (2007a) dataset indicates that there are systematic departures of predictions from the reference structures. Such systematic departures suggest one of the following: current alignment and structural models are deficient; 1000 iterations is not sufficient for reaching convergence; or several of the reference structures in the 17 Rfam families are not reflective of the structural and sequence features common to the RNA families. As shown in Supplementary Table S2, only two of the reference structures in this dataset were obtained by covariation analysis, and 13 were obtained by X-ray or NMR. Thus, nearly 76% of the reference structures in this dataset were determined by in vitro methods. Structures from such biophysical experiments may not reflect structural features common among family members, as important cellular components were likely missing in these experiments. This suggests an alternative goal for align-fold algorithms aimed at RNA family identification: correct classification of sequences into families, similar to that reported by Webb et al. (2002) for protein sequences. As the database of Rfam families has been obtained based on alignments to specific ‘reference structures,’ it will be a particularly difficult challenge to demonstrate that there is an alternative structure that is superior in the identification of family members. Thus, comparison of performances in family membership may require the use of reference sets obtained through independent experiments, such as those using immunoprecipitation (IP) methods. Finally, the existence of small variances indicates that an alternative estimator that trades larger variances for reduced bias may yield lower overall deviations.
4.4 Confusion of MEA
In recent publications (Do et al., 2006; Kiryu et al., 2007), MEA estimators are widely used as a better representative than the previous MFE estimator. However, we find the name MEA misleading. If the MEA is calculated on the basis of base pairs instead of individual bases, then this estimator corresponds to the centroid or γ -centroid. But our findings of large biases of these estimators indicate that expected ‘accuracy’ is misleading, in that there is no assurance that these estimators are close to an outside reference structure. However, these estimators do return estimates that have minimum variance, and thus in the least squared sense they are the most reproducible of all estimators in the posterior weighted space. Accordingly, they would be better described as maximum expected precision (MEP) estimators, or perhaps preferably by the non-buoyant name that defines them as centroid or γ-centroid estimates.
5 CONCLUSION
In this study, we introduce a blocked Gibbs sampler (RNAG) to predict secondary structure for unaligned RNA sequences. RNAG confronts the high time complexity of the align-fold problem by capitalizing on Liu's findings on blocked Gibbs sampling. Figures 1 and 2 show that the new algorithm delivers substantial improvement, as measured by PPV–SEN curves. However, as with any MCMC procedure, evidence of convergence during the burn-in cannot be guaranteed. Also, in the current implementation of this algorithm, little has been done ensure fast code or an efficient stopping rule. We found that the running times of RNAG are in the range of 3 times faster than the RNAsampler and 10 times slower than RAF. Thus, improvements in implementation speed will be important. While the results with the two available datasets and those shown in Supplementary Figure S3 are encouraging, these do not assure that this procedure will perform this well for all RNA sequence sets. Furthermore, this procedure and others like it may not be ideal for structure prediction since if it works perfectly, it will only capture structural and sequence features common to a set of input sequences, much as motif finding algorithms capture sequence characteristics common to transcription factor binding sites in multiple sequences. Nevertheless, here we show that RNAG does a better job at predicting reference structures than extant procedures, while providing a fuller characterization of the shape of the posterior space including characterization of multimodal features and ascertainment of uncertainty in structural predictions. Even if RNAG does continue to perform well at this task, several more steps will be necessary to develop a fully Bayesian RNA motif finder.
Supplementary Material
ACKNOWLEDGEMENTS
We thank Sean Eddy, Dave Mathews and the referees for their many helpful suggestions. We also thank Bill Thompson for his help improving the scripts for our implementation and Lee Ann McCue for helping to improve our presentation.
Funding: US Department of Energy, DOE grant (DOE: DE-FG02-04ER63942) and funds from Brown University.
Conflict of Interest: none declared.
REFERENCES
- Bindewald E., Shapiro B.A. RNA secondary structure prediction from sequence alignments using a network of k-nearest neighbor classifiers. RNA. 2006;12:342–352. doi: 10.1261/rna.2164906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernhart S.H., et al. RNAalifold: improved consensus structure prediction for RNA alignments. BMC Bioinformatics. 2008;9:474–487. doi: 10.1186/1471-2105-9-474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carvalho L., Lawrence C. Centroid estimation in discrete high-dimensional spaces with applications in biology. Proc. Natl Acad. Sci. USA. 2008;105:3209–3214. doi: 10.1073/pnas.0712329105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cary R.B., Stormo G.D. Graph-theoretic approach to RNA modeling using comparative data. Proc. Int. Conf. Intell. Syst. Mol. Biol. 1995;3:75–8. [PubMed] [Google Scholar]
- Chenna R., et al. Multiple sequence alignment with the Clustal series of programs. Nucleic Acids Res. 2003;31:3497–3500. doi: 10.1093/nar/gkg500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding Y., et al. RNA secondary structure prediction by centroids in a Boltzmann weighted ensemble. RNA. 2005;11:1157–1166. doi: 10.1261/rna.2500605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding Y., et al. Clustering of RNA secondary structures with application to messenger RNAs. J. Mol. Biol. 2006;359:554–571. doi: 10.1016/j.jmb.2006.01.056. [DOI] [PubMed] [Google Scholar]
- Do C.B., et al. ProbCons: probabilistic consistency-based multiple sequence alignment. Genome Res. 2005;15:330–340. doi: 10.1101/gr.2821705. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Do C.B., et al. CONTRAfold: RNA secondary structure prediction without physics-based models. Bioinformatics. 2006;22:e90–e98. doi: 10.1093/bioinformatics/btl246. [DOI] [PubMed] [Google Scholar]
- Do C.B., et al. A max-margin model for efficient simultaneous alignment and folding of RNA sequences. Bioinformatics. 2008;24:i68–i76. doi: 10.1093/bioinformatics/btn177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eddy S.R., Durbin R. RNA sequence analysis using covariance models. Nucleic Acids Res. 1994;22:2079–2088. doi: 10.1093/nar/22.11.2079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner P.P., et al. A benchmark of multiple sequence alignment programs upon structural RNAs. Nucleic Acids Res. 2005;33:2433–2439. doi: 10.1093/nar/gki541. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geman S., Geman D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE PAMI. 1984;6:721–741. doi: 10.1109/tpami.1984.4767596. [DOI] [PubMed] [Google Scholar]
- Giegerich R., et al. Abstract shapes of RNA. Nucleic Acids Res. 2004;32:4843–4851. doi: 10.1093/nar/gkh779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griffiths-Jones S., et al. Rfam: annotating non-coding RNAs in complete genomes. Nucleic Acids Res. 2005;33:D121–D124. doi: 10.1093/nar/gki081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gutell R.R., et al. Identifying constraints on the higher-order structure of RNA: continued development and application of comparative sequence analysis methods. Nucleic Acids Res. 1992;20:5785–5795. doi: 10.1093/nar/20.21.5785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamada M., et al. Prediction of RNA secondary structure using generalized centroid estimators. Bioinformatics. 2009;25:465–473. doi: 10.1093/bioinformatics/btn601. [DOI] [PubMed] [Google Scholar]
- Hamada M., et al. Improving the accuracy of predicting secondary structure for aligned RNA sequences. Nucleic Acids Res. 2011;39:393–402. doi: 10.1093/nar/gkq792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hofacker I.L., et al. Fast folding and comparison of RNA secondary structures. Monatshefte f. Chemie. 1994;125:167–188. [Google Scholar]
- Hofacker I.L., et al. Secondary structure prediction for aligned RNA sequences. J. Mol. Biol. 2002;319:1059–1066. doi: 10.1016/S0022-2836(02)00308-X. [DOI] [PubMed] [Google Scholar]
- Ji Y., et al. A graph theoretical approach for predicting common RNA secondary structure motifs including pseudoknots in unaligned sequences. Bioinformatics. 2004;20:1591–1602. doi: 10.1093/bioinformatics/bth131. [DOI] [PubMed] [Google Scholar]
- Kiryu H., et al. Murlet: a practical multiple alignment tool for structural RNA sequences. Bioinformatics. 2007a;23:1588–1598. doi: 10.1093/bioinformatics/btm146. [DOI] [PubMed] [Google Scholar]
- Kiryu H., et al. Robust prediction of consensus secondary structures using averaged base pairing probability matrices. Bioinformatics. 2007b;23:434–441. doi: 10.1093/bioinformatics/btl636. [DOI] [PubMed] [Google Scholar]
- Knudsen B., Hein J. RNA secondary structure prediction using stochastic context-free grammars and evolutionary history. Bioinformatics. 1999;15:446–454. doi: 10.1093/bioinformatics/15.6.446. [DOI] [PubMed] [Google Scholar]
- Lindgreen S., et al. MASTR: multiple alignment and structure prediction of non-coding RNAs using simulated annealing. Bioinformatics. 2007;23:3304–3311. doi: 10.1093/bioinformatics/btm525. [DOI] [PubMed] [Google Scholar]
- Liu J.S. The collapsed Gibbs Sampler in Bayesian computations with applications to a gene regulation problem. J. Am. Stat. Assoc. 1994;89:958–966. [Google Scholar]
- Mathews D.H. Using an RNA secondary structure partition function to determine confidence in base pairs predicted by free energy minimization. RNA. 2004;10:1178–1190. doi: 10.1261/rna.7650904. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathews D.H. Revolutions in RNA secondary structure prediction. J. Mol. Biol. 2006;359:526–532. doi: 10.1016/j.jmb.2006.01.067. [DOI] [PubMed] [Google Scholar]
- Meyer I.M., Miklos I. SimulFold: simultaneously inferring RNA structures including pseudoknots, alignments, and trees using a Bayesian MCMC framework. PLoS Comput. Biol. 2007;3:e149. doi: 10.1371/journal.pcbi.0030149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nawrocki E.P., Eddy S.R. Query-dependent banding (QDB) for faster RNA similarity searches. PLoS Comput. Biol. 2007;3:e56. doi: 10.1371/journal.pcbi.0030056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nawrocki E.P., et al. Infernal 1.0: inference of RNA alignments. Bioinformatics. 2009;25:1335–1337. doi: 10.1093/bioinformatics/btp157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newberg L.A., Lawrence C.E. Exact calculation of distributions on integers, with application to sequence alignment. J. Comput. Biol. 2009;16:1–18. doi: 10.1089/cmb.2008.0137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakakibara Y., et al. Stochastic context-free grammers for tRNA modeling. Nucleic Acids Res. 1994;22:5112–5120. doi: 10.1093/nar/22.23.5112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sankoff D. Simultaneous solution of the RNA folding, alignment and protosequence problems. SIAM J. Appl. Math. 1985;45:810–825. [Google Scholar]
- Seemann S.E., et al. Unifying evolutionary and thermodynamic information for RNA folding of multiple alignments. Nucleic Acids Res. 2008;36:6355–6362. doi: 10.1093/nar/gkn544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siebert S., Backofen R. MARNA: multiple alignment and consensus structure prediction of RNAs based on sequence structure comparisons. Bioinformatics. 2005;21:3352–3359. doi: 10.1093/bioinformatics/bti550. [DOI] [PubMed] [Google Scholar]
- Steffen P., et al. RNAshapes: an integrated RNA analysis package based on abstract shapes. Bioinformatics. 2006;22:500–503. doi: 10.1093/bioinformatics/btk010. [DOI] [PubMed] [Google Scholar]
- Tabaska J.E., et al. An RNA folding method capable of identifying pseudoknots and base triples. Bioinformatics. 1998;14:691–699. doi: 10.1093/bioinformatics/14.8.691. [DOI] [PubMed] [Google Scholar]
- Torarinsson E., et al. Multiple structural alignment and clustering of RNA sequences. Bioinformatics. 2007;23:926–932. doi: 10.1093/bioinformatics/btm049. [DOI] [PubMed] [Google Scholar]
- Webb B.M., et al. BALSA: Bayesian algorithm for local sequence alignment. Nucleic Acids Res. 2002;30:1268–1277. doi: 10.1093/nar/30.5.1268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Webb-Robertson B.M., et al. Measuring global credibility with application to local sequence alignment. PLoS Comput. Biol. 2008;4:e1000077. doi: 10.1371/journal.pcbi.1000077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Will S., et al. Inferring noncoding RNA families and classes by means of genome-scale structure-based clustering. PLoS Comput. Biol. 2007;3:e65. doi: 10.1371/journal.pcbi.0030065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xing X., et al. RNA Sampler: a new sampling based algorithm for common RNA secondary structure prediction and structural alignment. Bioinformatics. 2007;23:1883–1891. doi: 10.1093/bioinformatics/btm272. [DOI] [PubMed] [Google Scholar]
- Yao Z., et al. CMfinder - a covariance model based RNA motif finding algorithm. Bioinformatics. 2006;22:445–452. doi: 10.1093/bioinformatics/btk008. [DOI] [PubMed] [Google Scholar]
- Zuker M., Stiegler P. Optimal computer folding of large RNA sequences using thermodynamics and auxiliary information. Nucleic Acids Res. 1981;109:133–148. doi: 10.1093/nar/9.1.133. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.