Dynamics May Significantly Influence the Estimation of Interatomic Distances in Biomolecular X-ray Structures

Abstract

Atomic positions obtained by X-ray crystallography are time and space averages over many molecules in the crystal. Importantly, interatomic distances, calculated between such average positions and frequently used in structural and mechanistic analyses, can be substantially different from the more appropriate time-average and ensemble-average interatomic distances. Using crystallographic B-factors, one can deduce corrections, which have so far been applied exclusively to small molecules, to obtain correct average distances as a function of the type of atomic motion. Here, using 4774 high-quality protein X-ray structures, we study the significance of such corrections for different types of atomic motion. Importantly, we show that for distances shorter than 5 Å, corrections greater than 0.5 Å may apply, especially for noncorrelated or anticorrelated motion. For example, 14% of the studied structures have at least one pair of atoms with a correction of ≥ 0.5 Å in the case of noncorrelated motion. Using molecular dynamics simulations of villin headpiece, ubiquitin, and SH3 domain unit cells, we demonstrate that the majority of average interatomic distances in these proteins agree with noncorrelated corrections, suggesting that such deviations may be truly relevant. Importantly, we demonstrate that the corrections do not significantly affect stereochemistry and the overall quality of final refined X-ray structures, but can provide marked improvements in starting unrefined models obtained from low-resolution X-ray data. Finally, we illustrate the potential mechanistic and biological significance of the calculated corrections for KcsA ion channel and show that they provide indirect evidence that motions in its selectivity filter are highly correlated.

Graphical Abstract

Research Highlights

► We obtain corrected interatomic distances from static X-ray structures and B-factors. ► For a large set of protein structures, we show that corrections may exceed 0.5 Å. ► Molecular dynamics simulations agree best with noncorrelated corrections. ► Use of corrected distances in refinement frequently lowers the R_free factor. ► Corrections give indirect evidence of correlated motions in KcsA selectivity filter.

Introduction

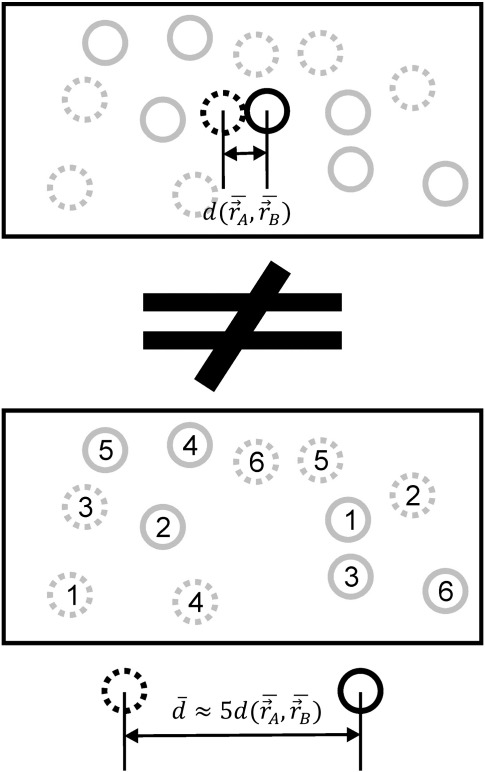
From an examination of active-site geometries to a mechanistic analysis of functionally important conformational changes in biomolecules, assessment of interatomic distances is an important element in most studies of biomolecular X-ray structures. However, it should be borne in mind that the X-ray structures deposited in the Protein Data Bank (PDB) are derived from measurements that are time and space averages over many dynamic, structurally heterogeneous conformers contained in the crystal.^1,2 One issue arising from such averaging is that the interatomic distances calculated from experimentally obtained average atomic positions may be significantly different from the corresponding time-average and ensemble-average distances due to the nonlinear relation between atomic distance and position. Simply put, the distance between average positions is not the same as the average distance. In Fig. 1, we show a simple example illustrating this point. Two atoms (one depicted with a continuous line and one depicted with a dotted line) move inside a box, and we compare the distance between their average positions (top) with the average distance between them over time (bottom). In the latter case, the positions of the two atoms at equivalent time points are indicated by sequential indices (Fig. 1, bottom). As shown in the figure, the distance between the average positions of the two atoms is approximately five times shorter than the average distance between them over time, illustrating how dramatic the above effect can be in principle.

Fig. 1.

Interatomic distances calculated from average atomic positions may significantly differ from time-average and ensemble-average distances. To illustrate this, we show a simple system with the positions of two gray circles over time (continuous and broken). In the upper rectangle, the average positions of the two circles are shown in black, and their distance is marked with $d\left(\overline{{\overrightarrow{r}}_{\text{A}}},\overline{{\overrightarrow{r}}_{\text{B}}}\right)$. In the lower rectangle, the distance between circles is calculated for each time point and then averaged linearly over time. The average distance is shown in black; for this system, it is actually five times greater than the distance between the average positions $\bar{d}\approx 5d\left(\overline{{\overrightarrow{r}}_{\text{A}}},\overline{{\overrightarrow{r}}_{\text{B}}}\right)$.

While the average distances are more appropriate and more rigorous in terms of statistical mechanics, in most practical applications, one uses distances between the average atomic positions reported in PDB files. In order to address this discrepancy in the case of small molecules, Busing and Levy derived corrections to distances between average positions to obtain average distances by using crystallographic B-factors.³ Importantly, in their derivation, they require that the type of interatomic motion (correlated, noncorrelated, or anticorrelated) is known or can be assumed. The Busing–Levy corrections have been extensively used over the years almost exclusively on small molecules due primarily to the complexity of macromolecules and their dynamics.^4,5 Here, we apply the Busing–Levy formalism to a large number of known protein structures obtained from the PDB in order to study the magnitude of the corrections assuming different types of atomic motion. We show that for short distances, large corrections may apply, especially in cases of noncorrelated and anticorrelated atomic motions.

While these corrections may be sizable, it is not a priori clear how correlated atomic motions are in typical proteins.^6–12 Molecular dynamics (MD) simulations have played a leading role in this regard, and a variety of different behaviors, ranging from highly correlated motion to highly anticorrelated motion, have been observed for different systems.^7,10–12 To address this question in the present context, we have performed a set of MD simulations of the crystallographic unit cells of the villin headpiece, ubiquitin, and SH3 domain from which we directly calculate the following: (1) the time-average and ensemble-average interatomic distances; (2) the distances between time-average and ensemble-average positions; and (3) the corrections to the latter based on B-factors derived from root-mean-square fluctuations (RMSFs).¹³ A comparison between these three values calculated for the simulated structures has subsequently allowed us to determine what type of corrections calculated from B-factors would be most appropriate for typical proteins. Force-field imperfections notwithstanding, the main advantage of such an analysis is that it is fully self-consistent (i.e., we compare distances between average positions and average distances within the same model). Finally, we analyze the effect of the corrections on the stereochemistry of refined X-ray structures and refinement quality measures such as the R_free factor. On the whole, the effect of the corrections on the final deposited structures is minor. However, when using starting structures from molecular replacement, we observed a noticeable improvement.

What is the biological significance of the discussed corrections? As a test case, we calculate the corrections for an X-ray structure of the transmembrane part of the KcsA ion channel¹⁴ to study their potential effects. This bacterial channel is known for its selectivity for potassium ions over sodium ions by a factor of 10⁴. Such a high preference for potassium ions has been explained by a fine-tuned solvation of dehydrated ions by the carbonyl oxygens of amino acids in the channel's selectivity filter (the TVGYG motif) and by the fact that such solvation is deemed impossible for sodium ions due to their smaller radius.^15,16 Naturally, a measurement of interatomic distances in the filter is a key element in any quantitative analysis of such effects. Importantly, there have been several reports on the correlated motion of ions and carbonyl groups inside the selectivity filter indicative of its flexibility.^17–21 Here, we demonstrate the potential mechanistic and biological significance of the distance corrections in the case of the selectivity filter of the KcsA ion channel and show that the type of motion in it can actually be determined indirectly through the calculated corrections.

Results

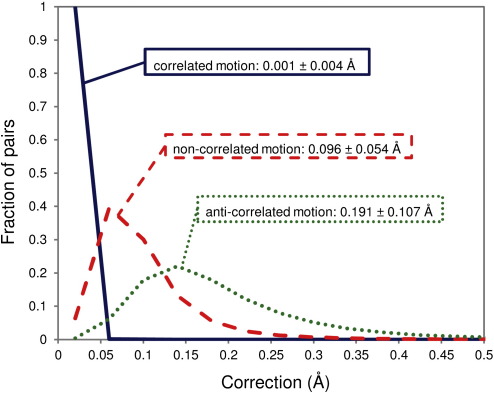
We have applied the Busing–Levy method³ to a set of 4774 high-quality protein X-ray structures assuming different types of motion for each selected atomic pair in each structure. For the analysis, we chose those pairs of atoms that are close in space (< 5 Å) in a given reported structure, as the corrections are inversely proportional to separation (see Methods) and are potentially sizeable only for relatively short separations. Moreover, we only chose atoms that are separated sufficiently in protein sequence (≥ 5 residues) to avoid situations where correlated motion dominates simply due to covalent connectivity. The distributions of calculated corrections to distances between average atomic positions for all motion types, together with their arithmetic means and standard deviations, are shown in Fig. 2. In the case of the distributions of corrections for fully correlated motion, calculated values of more than 99% of atomic pairs are smaller than 0.04 Å (Fig. 2) and 1% (Fig. S2), with arithmetic means of the distributions of 0.001 ± 0.004 Å and 0.026 ± 0.090%, respectively. However, the distributions of corrections for noncorrelated and anticorrelated motions are substantially wider, with a long right-hand-side tail showing that there is a significant number of atomic pairs in both cases for which the corrections are larger than 0.5 Å and 15% (Fig. 2; Fig. S2). The arithmetic means of the distributions of noncorrelated corrections are 0.096 ± 0.054 Å and 2.300 ± 1.464%, while they are 0.191 ± 0.107 Å and 4.575 ± 2.907% for the distributions of anticorrelated corrections.

Fig. 2.

Distributions of corrections to distances between average atomic positions calculated for a collection of X-ray structures (4774 structures) assuming different types of interatomic motion: correlated (continuous blue curve), noncorrelated (broken red curve), and anticorrelated (dotted green curve), with their arithmetic means and standard deviations. All values were binned in 0.04-Å bins to generate the distributions.

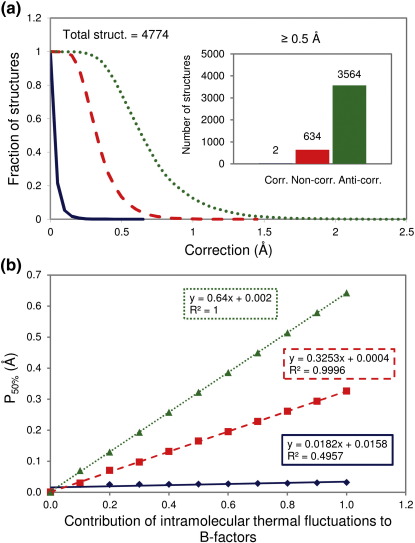
Clearly, at the level of population means, the corrections are relatively small for all three types of motion studied. However, this should not be confused with the fact that in almost every one of the studied structures, there is a subset of atoms for which corrections are significantly more dominant. To examine this more closely, we report the number of structures that have at least one pair of atoms with a distance correction corresponding to or greater than a given value, assuming different types of motion (Fig. 3a). It can be seen that for almost every structure in our set, there is at least one pair of atoms that exhibits a correction greater than 0.2 Å if the interatomic motion is assumed to be noncorrelated or anticorrelated. Moreover, almost 15% of all structures in our data set have at least one pair of atoms with a correction of ≥ 0.5 Å for noncorrelated motion, while for anticorrelated motion, the number increases to almost 75% of all structures. In order to more closely study these atoms most affected by such corrections, we have determined whether they belong to residues on the protein surface or residues in the protein core. To determine which residues in a given protein are on its surface, we divided the solvent-accessible surface area of the residue in question by its solvent-accessible surface area when fully exposed to solvent. If this fraction is higher than 0.2, we consider the residue to be on the surface of a given protein, and vice versa. Briefly, in 28% of all of the analyzed pairs, both atoms belong to a surface residue regardless of the type of motion; in 44% of the pairs, one atom belongs to a surface residue and one atom belongs to a core residue; and in 28% of the pairs, both atoms belong to core residues. These percentages do not change significantly if we calculate them for all the analyzed pairs, and not only for those with such high corrections.

Fig. 3.

(a) Fraction of structures that have at least one pair of atoms for which the correction is equal to or greater than a given value (in steps of 0.05 Å), assuming three types of motion: correlated (continuous blue curve), noncorrelated (broken red curve), and anticorrelated (dotted green curve). Inset: Exact numbers are given for corrections greater than 0.5 Å, with the same color code. (b) Cutoff where 50% of the structures exhibit at least one interatomic distance with a correction greater than or equal to it (P_50%), as a function of the contribution of intramolecular thermal fluctuations to B-factors (the color code for types of motion is the same as in (a)).

In our calculations, we have assumed that the B-factors reported in PDB files originate exclusively from intramolecular atomic fluctuations. However, the question of how much thermal fluctuations actually contribute to crystallographic B-factors is a matter of long-standing debate.^7,22–24 Considering this, we have recalculated the distributions given in Fig. 3a assuming different levels of contribution of intramolecular thermal fluctuations to B-factors used in the equations. As a summary of this analysis, we report in Fig. 3b the values (P_50%) for which 50% of the structures in our data set have at least one interatomic pair with a corresponding or greater correction. It can be seen that the effect on those values is linearly proportional to the level of contribution of intramolecular fluctuations to B-factors for all types of motion. For example, even if only one-half of the reported B-factors comes from intramolecular fluctuations, still more than 50% of the structures in our set would exhibit at least one correction greater than 0.18 Å.

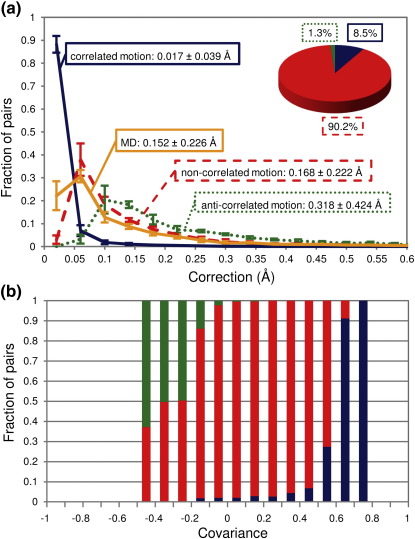
The corrections discussed herein depend directly on the type of atomic motion involved. At this point, it is important to ask how correlated atomic motions are in a typical protein. To address this question, we have performed MD simulations of the crystallographic unit cells of the villin headpiece (all-α-fold), ubiquitin (α/β-fold), and SH3 domain (all-β-fold) in order to obtain and compare time-average and ensemble-average distances between atoms, on one hand, with the distances between time-average and ensemble-average positions corrected for motional effects using B-factors, on the other hand. The latter can be derived directly from MD simulations from atom-positional RMSFs by using Eq. (5) (see Methods). The distributions of calculated corrections, based on five independent 20-ns-long simulations of ubiquitin molecules in the unit cell, are shown in Fig. 4a (absolute value) and Fig. S3 (percentages). The arithmetic means of the distributions are as follows: 0.017 ± 0.039 Å and 0.415 ± 0.964% for correlated corrections; 0.168 ± 0.222 Å and 4.132 ± 5.952% for noncorrelated corrections; and 0.318 ± 0.424 Å and 7.849 ± 11.404% for anticorrelated corrections.

Fig. 4.

(a) Distributions of corrections to interatomic distances calculated for structures obtained from MD simulations of the unit cell of ubiquitin's crystal, assuming three different types of motion: correlated (continuous blue curve), noncorrelated (broken red curve), and anticorrelated (dotted green curve). The distribution of differences between average interatomic distances and distances from average positions (also obtained directly from MD simulations) is shown as a continuous orange curve, with the arithmetic means and standard deviations for every distribution also given. All the values were binned in 0.04-Å bins to generate the distributions. Inset: Relationship between average instantaneous distances and corrections, assuming different types of motion. The percentage of atomic pairs whose average distance is closest to the one obtained from the corrections: 8.5% for correlated motion (blue), 90.2% for noncorrelated motion (red), and 1.3% for anticorrelated motion (green). (b) Normalized positional covariances between pairs of atoms used for calculations from an MD simulation of ubiquitin's crystallographic unit cell. Values are binned in 0.1 bins and color coded according to the closeness of the average distance to the correction for a specific type of motion (correlated, blue; noncorrelated, red; anticorrelated, green).

How do the calculated corrections compare with the differences between the average interatomic distances and the distances between the average positions obtained from the simulated trajectories? Interestingly, across different values, the distribution of the latter differences (with arithmetic means of 0.152 ± 0.226 Å and 3.759 ± 6.162%) is closest to the distribution of corrections in the case of noncorrelated motion. In fact, ≈ 90% of the studied atomic pairs in ubiquitin exhibit an average distance that is closest to the one obtained using the correction for noncorrelated motion (Fig. 4a, inset). In addition, we performed similar simulations of ubiquitin in solution with two different starting structures: the X-ray structure 1UBI^25,26 and the solution NMR structure 1D3Z²⁷ (see Supplementary Data, Figs. S4 and S5). Notably, the distributions of the aforementioned values do not change significantly for the solution simulations of ubiquitin, regardless of the starting structure. Moreover, the results for the simulations of villin headpiece molecules (Fig. S6a and b) and SH3 domain molecules (Fig. S6c and d) match the ubiquitin results to within a few percentages: approximately 85% and 95% of the studied atomic pairs in the villin headpiece and SH3 domain, respectively, exhibit an average distance that is closest to the one obtained using the correction for noncorrelated motion (Fig. S6a and c, insets). Taken together, our results suggest that for these proteins and even for short interatomic separations, the motion of the studied nonbonded atoms is likely to be mostly noncorrelated, meaning that these corrections should be the most relevant ones. Here, it is important to mention that our MD simulation analysis is completely self-consistent, as we calculate both average positions and distances between them, as well as B-factors and dynamics-based corrections from the same simulated ensembles. However, it is possible that imperfections in the force fields used introduce some biases in the degree of correlation of atomic motions. While this possibility is extremely difficult to test further at the present moment, primarily because of a lack of quality experimental results with sufficient resolution, it should be borne in mind.

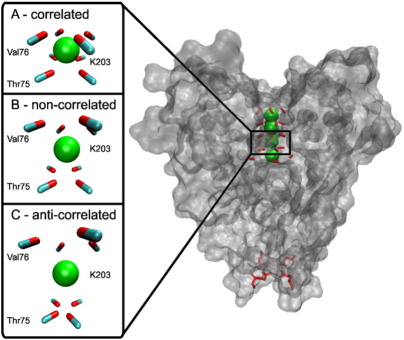
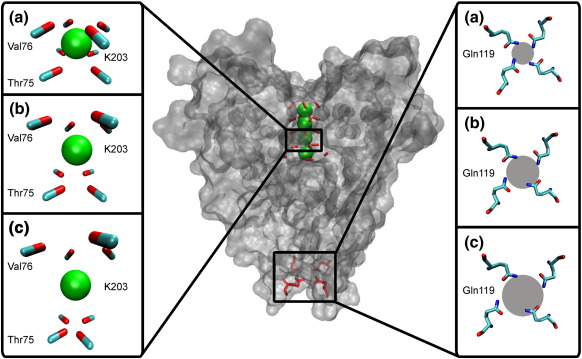
The above examples suggest that, in some cases, time-average and ensemble-average interatomic distances may be more than 0.5 Å greater than the distance between average atomic positions. How biologically significant is this? Here, we would like to suggest that this difference may indeed have important consequences for considerations of biological mechanisms. The KcsA ion channel is an illustrative example of a biomolecular structure where distances between atoms and their orientation play a key role in the molecule's function (i.e., ionic selectivity, as described in the Introduction). Therefore, using a 2.8-Å-resolution X-ray structure of the channel (PDB ID: 1J95), we have calculated the corrections to average distances between the backbone carbonyl groups of Thr75 and Val76 (part of the TVGYG motif in the selectivity filter) and the potassium ion (K203), which these carbonyl groups coordinate. Corrections were also calculated for the N^ε atom of Gln119 located at the end of the channel's cavity (the gate). Based on the corrected average distances, we generated configurations showing how these specific parts of the channel would look like if their interatomic distances corresponded to the actual corrected average distances under three types of motion (Fig. 5). The results are striking. The average corrections for the assumption of noncorrelated motion are Thr75C-K203 = 16% (4.3 Å versus 3.7 Å), Thr75O-K203 = 35% (3.5 Å versus 2.6 Å), Val76C-K203 = 17% (4.0 Å versus 3.4 Å), Val76O-K203 = 26% (3.4 Å versus 2.7 Å), and Gln119N^ε-Gln119N^ε = 39% (4.3 Å versus 3.1 Å), while the average corrections for anticorrelated motion are Thr75C-K203 = 30% (4.8 Å versus 3.7 Å), Thr75O-K203 = 65% (4.3 Å versus 2.6 Å), Val76C-K203 = 35% (4.6 Å versus 3.4 Å), Val76O-K203 = 52% (4.1 Å versus 2.7 Å), and Gln119N^ε-Gln119N^ε = 81% (5.6 Å versus 3.1 Å). Based on this, one can indirectly conclude that correlated motion is the only kind of motion that is still consistent with the channel's function. Namely, the structure of the channel, which would simultaneously agree with the measured B-factors and either noncorrelated or anticorrelated motion corrections, would be highly distorted (Fig. 5). As the above numbers show, the cross section of the narrowest part of the channel (i.e., its selectivity filter) would significantly increase in surface area for noncorrelated correction, and even more so for anticorrelated correction, having direct implications on the size and coordination properties of ions that can pass through it (i.e., on the channel's selectivity).

Fig. 5.

Configurations based on average interatomic distances obtained by correcting distances between average positions in two locations of the KcsA ion channel (PDB ID: 1J95).²⁸ The corrections on the left-hand side of the figure are calculated for the carbonyl group (carbon atom, light blue; oxygen atom, red) of Thr75 and Val76 (in the selectivity filter) and the potassium ion K203 (green), and they represent one possible structure of the particular part of the filter assuming different types of motion: (a) correlated, (b) noncorrelated, and (c) anticorrelated. On the right-hand side of the figure, the corrections are calculated for the N^ε atoms (dark blue) of Gln119 located at the end of the channel's cavity (the gate), also assuming various types of motion. The radii of gray circles are averages of distances between the opposite N^ε atoms. All the structures in the figure have been prepared by VMD version 1.8.6.²⁹

Discussion

X-ray crystallography is widely considered to be the most powerful method for determining structures of biomolecules with subangstrom precision. Here, our application of the Busing–Levy method³ for the correction of distances between average positions reveals that there are numerous protein X-ray structures with atom pairs whose corrected distance is 0.5 Å (or more) larger than the distance in the X-ray structure calculated from average atomic positions, assuming the motion is noncorrelated or anticorrelated (Fig. 2). Moreover, such examples imply that there are cases where the corrections can have a significant influence on the conclusions drawn from structural analysis and should not be disregarded. Note that the motional effects discussed here are largely independent of the equally relevant issue of how precisely the average atomic coordinates are determined. The precision of atomic coordinates in PDB structures, which are given to one-thousandth of an angstrom in PDB files, actually depends on the resolution of a given structure and the B-factor of the atom in question, and can vary greatly from one-hundredth an angstrom to several tenths of an angstrom, even for high-resolution structures.^1,30,31 However, it should be strongly emphasized that the dynamics-based corrections addressed in this study are fully independent of the uncertainty in interatomic distances originating from the uncertainty in average atomic positions. Even if the average atomic positions were determined with infinite precision, the dynamics-based corrections would still be there as a consequence of the fact that distance between average positions is not the same as the average distance, as discussed above. In other words, imprecision in average atomic coordinates acts in tandem with the dynamics-related corrections discussed herein; this further means that the corrections can exhibit uncertainty themselves (and can actually even be larger) just due to the error in the average coordinates. Equations for the propagation of error in average atomic coordinates to the corrected distances can be found in Supplementary Data. The effect of dynamics and intrinsic coordinate precision could be studied by comparing the corrected distances to distances measured with more precision by, for example, advanced NMR techniques.⁸

In an effort to learn more about the range of validity of the different types of assumed atomic motions, we have simulated the unit cells of the crystal villin headpiece, ubiquitin, and SH3 domain. This has enabled us to calculate the corrections based on the B-factors derived from a measure often used in MD RMSF and to compare them to average interatomic separations of atoms that were also obtained directly from the simulations (Fig. 4a; Fig. S6a and c). One might expect that, at the close separations studied here (< 5 Å), the average distances would be closest to the distances corrected for correlated motion. Note that correlated motion has been observed in previous computational studies for closely packed atoms.^6,7 In fact, one of the molecules studied here—ubiquitin—has frequently been used to study the timescales of internal motions and the levels of structural fluctuations in proteins. For example, Lindorff-Larsen et al.³² reported a liquid-like behavior of the interior atoms in ubiquitin, indicating significant mobility, while Clore and Schwieters³³ detected correlations between N–H bond vectors that are generally limited to sequentially neighboring residues, but also appear in long-range vector pairs that are close in space (although their correlations are not very prominent). On the other hand, Li et al. showed that over 98% of protein dihedral-angle pairs in ubiquitin are in fact uncorrelated.³⁴ However, we can conclude from our analysis of the aforementioned proteins that the majority of atomic pairs separated by less than 5 Å (and at least five residues apart in sequence) exhibit average distances closest to the correction for noncorrelated motion (Fig. 4a; Fig. S6a and c). How can one explain this in light of the fact that significant correlated motions have been observed in proteins, as discussed above? The resolution of this seeming paradox is reached if one recognizes that a better agreement with noncorrelated corrections than with correlated corrections does not mean that the atomic motions are necessarily fully noncorrelated. In fact, analysis of our simulations shows that even for atomic pairs whose normalized positional covariance exceeds 0.6, one can, in some cases, get average interatomic distances that agree better with noncorrelated corrections than with correlated corrections (Fig. 4b; Fig. S6b and d). Overall, the majority of pairs with positional covariances between approximately − 0.4 and 0.5 (and this is the majority of studied atoms) exhibit average distances closest to the noncorrelated correction (Fig. 4b; Fig. S6b and d). Fully correlated motions are likely present only for nonbonded atoms that are in direct van der Waals contact, while noncorrelated motions dominate at larger separations. Note also that, in our analysis, we purposefully excluded atomic pairs whose motion could be correlated just by chain connectivity (i.e., those whose sequence separation was < 5 residues).

Using distance-restraining methods and corrections discussed herein, one can, in principle, refine structural models of biomolecules, which, instead of capturing correct average atomic positions, capture correct interatomic distances. Following this approach, we have refined three protein structures (villin headpiece, PDB ID: 2RJY; ubiquitin, PDB ID: 3EFU; SH3 domain, PDB ID: 1H8K)^35–37 using in the refinement distance restraints that correspond to the Busing–Levy corrections based on B-factors derived from unrestrained refinement. As an additional control, we also perform refinement with distance restraints derived from the same structure, but without any corrections. The results of this procedure are summarized in Table 1, where it can be seen that distance corrections have varied effects when applied to refinement using the final structures deposited in the PDB (Table 1). In particular, while including the restraints had a positive effect on R_free in the refinement of the SH3 domain 1H8K structure compared to the unrestrained case (0.324 versus 0.360), there was little or no effect (0.227 versus 0.232) for the villin headpiece 2RJY structure, and the effect was reversed (0.318 versus 0.338) for the ubiquitin 3EFU structure. There are several challenges in this regard. First, it is difficult to know a priori what motional model to apply to a given pair of atoms for deriving corrections. However, as discussed above, our simulations suggest that about 90% of all pairs of atoms exhibit average distances closest to the noncorrelated correction, 9% of all pairs of atoms exhibit average distances closest to the correlated correction, and 1% of all pairs of atoms exhibit average distances closest to the anticorrelated correction (Fig. 4a). In agreement with this, in the present examples, we have imposed on each pair of atoms a correction that is a weighted average of the three types of corrections in accordance with these percentages. This is obviously a simplification; however, in the absence of any other information, it is likely a reasonable approach to follow. Second, the corrections discussed here are all of pairwise nature, and it is not clear how they translate to many-body situations. Finally, even if one has a set of correct average interatomic distances, it is difficult to find a single three-dimensional structure that fully satisfies them all, and this problem grows with the number of atoms (i.e., distances) involved. For example, only about 50% of all distances in the present examples have the target distances better matched in the restrained structure than in the unrestrained structure (Table 1). Interestingly, a significant improvement in R_free (0.324 versus 0.360) is seen for the SH3 domain structure, which is where target corrected distances are best matched (Table 1).

Table 1.

Refinement details for the SH3 domain (PDB ID: 1H8K), villin headpiece (PDB ID: 2RJY), and ubiquitin (PDB ID: 3EFU)

	PDB ID 1H8K				PDB ID 2RJY				PDB ID 3EFU
	unrestr0	unrestr	restr	restror	unrestr0	unrestr	restr	restror	unrestr0	unrestr	restr	restror
R	0.237	0.233	0.248	0.245	0.202	0.202	0.205	0.206	0.210	0.226	0.250	0.245
Rfree	0.324	0.360	0.324	0.312	0.227	0.227	0.232	0.231	0.308	0.318	0.338	0.334
RMS (Å)	0.104	0.150	0.111	0.106	0.116	0.116	0.119	0.116	0.130	0.187	0.164	0.147
Distance match (%)	13.8	19.7	59.0	7.5	20.0	22.1	44.5	13.4	18.3	25.7	46.6	9.4
RMS bond length (Å)	0.012	0.017	0.013	0.015	0.027	0.028	0.027	0.026	0.148	0.070	0.072	0.070
RMS bond angle (°)	1.395	1.789	1.459	1.529	2.200	2.278	2.198	2.131	1.926	1.560	1.710	1.946
RMS chiral volume (Å3)	0.091	0.120	0.104	0.102	0.143	0.148	0.138	0.136	0.133	0.096	0.095	0.114

RMSD is calculated between the interatomic distances used as restraints in the refinement and the distances in each of the models, as well as for the following stereochemical quantities: bond lengths, bond angles, and chiral volumes. Distance match for each model represents the percentage of interatomic distances closest to the calculated restraints compared to the distances in the other two models. The following labels apply: unrestr₀—structure refined without external restraints; unrestr—structure refined from unrestr₀ without external restraints; restr—structure refined from unrestr₀ using corrections calculated according to Busing–Levy equations as restraints; restr_or—structure refined from unrestr₀ using distances without any corrections as restraints.

Similarly, a marked improvement is observed when using molecular replacement starting models, particularly with low-resolution data (Table 2). When starting refinement with the molecular replacement models and distance restraints for the 1H8K and 3EFU structures, we obtained significantly improved R_free values when corrected distance restraints were used (Table 2), with generally a small effect on stereochemistry. Specifically, R_free dropped from 0.409 to 0.358 for the SH3 domain 1H8K structure, and from 0.352 to 0.329 for the ubiquitin 3EFU structure, compared with the model refined using no restraints. Moreover, for the lower-resolution 1H8K case, the introduction of the corrected distance restraints led to much less overfitting, as seen by a smaller difference between the R factor and the R_free factor. It can also be seen that the use of corrected distance restraints in the refinement results in a much lower R_free factor than the use of the uncorrected restraints for the SH3 domain 1H8K structure (0.358 versus 0.396), with no significant difference for the ubiquitin 3EFU structure (0.329 versus 0.322). Further work should be directed at exploring this potentially exciting approach for improving the quality of refined X-ray structures: using corrected distances may be a powerful restraint for improving the convergence of X-ray structure refinement, particularly with low-resolution data.

Table 2.

Molecular replacement details for the SH3 domain (PDB ID: 1H8K) and ubiquitin (PDB ID: 3EFU)

	PDB ID 1H8K				PDB ID 3EFU
	start	unrestr	restr	restror	start	unrestr	restr	restror
R	0.458	0.248	0.301	0.368	0.374	0.273	0.277	0.279
Rfree	0.438	0.409	0.358	0.396	0.396	0.352	0.329	0.322
RMS (Å)	0.158	0.493	0.372	0.186	0.065	0.268	0.157	0.129
Distance match (%)	22.4	15.5	38.8	23.3	30.2	8.1	52.3	9.4
RMS bond length (Å)	0.021	0.013	0.013	0.015	0.020	0.022	0.023	0.022
RMS bond angle (°)	2.762	1.507	1.629	1.965	3.006	2.002	2.220	2.186
RMS chiral volume (Å3)	0.188	0.081	0.099	0.128	0.175	0.140	0.157	0.138

RMSD is calculated between the interatomic distances used as restraints in the refinement and the distances in each of the models, as well as for the following stereochemical quantities: bond lengths, bond angles, and chiral volumes. Distance match for each model represents the percentage of interatomic distances closest to the restraints compared to the distances in the other two models. The following labels apply: start—molecular replacement solution; unrestr—structure refined without external restraints; restr—structure refined using corrections calculated according to Busing–Levy equations as restraints (the restraints were calculated for PDB ID 1H8K from the 1SHG model and for PDB ID 3EFU from the 1UBQ model); restr_or—structure refined from unrestr₀ using distances without any corrections as restraints.

In addition, we have obviated most of the refinement problems by exclusively focusing on a small but important number of atoms in the case of the KcsA channel (Fig. 5). However, it should be stressed that structural representations capturing corrected distances in Fig. 5 depend on the total number of interatomic distances and atoms involved in the calculation, and are used only for illustration purposes. Nonetheless, we are still able to indirectly conclude that the motion between the selected atoms must be highly correlated, confirming previous findings^17–21 in a completely novel and orthogonal way.

The principal assumption behind all of the above analyses and applied corrections is that crystallographic B-factors report exclusively on the intramolecular dynamics of the biomolecule in question. Of course, other factors such as crystal lattice defects, rigid-body motions, occupancy levels, or refinement artifacts can and do contribute to the observed B-factors.^7,38–40 Furthermore, they also contain components coming from both static disorder and dynamic disorder,^41,42 whose separation is nontrivial.⁷ In addition, it is difficult to tell whether the refinement has been conducted using the state-of-the-art software at the time of deposition and whether the software has been used in an optimal manner.⁴³ Until all of the mentioned artifacts are fully resolved and understood, making assumptions based on a comparison of simulations and secondary or derived data can result in overinterpreted or misinterpreted conclusions.⁴⁴ In this sense, corrections discussed herein should be taken as upper limits derived under the premise that B-factors report exclusively on intramolecular dynamics (for further discussion on the drawbacks of using both B-factors and MD simulations to study biomolecular dynamics, please refer to an insightful study by Meinhold and Smith⁷). The effect of varying the level of dynamic contribution to B-factors is analyzed in Fig. 3b; it is largely linearly proportional to the fraction of B-factors coming from intramolecular fluctuations and can be significant even if this fraction is far from 100% (Fig. 3b). In conclusion, these kinds of analysis can provide insight into protein dynamics that may be obscured by time averaging and space averaging occurring in X-ray crystallography experiments. Even more importantly, they should inspire caution when analyzing X-ray structures and studying biological mechanisms. In particular, we expect them to be highly relevant to all situations where short interatomic distances are of critical importance, such as in the analysis of enzymatic reaction mechanisms, drug design applications, or structure-based quantum mechanics/molecular mechanics simulations.

Materials and Methods

Busing–Levy equations for distance corrections

Here we present equations for calculating corrections of interatomic distances derived by Busing and Levy in their original study (for the derivation, refer to Supplementary Data).³ If the motion of two atoms in question is assumed to be correlated, the corrected distance is:

$$\bar{S}=S_0+{\left[{\left(\overline{w_{\text{B}}^2}\right)}^{\frac{1}{2}}-{\left(\overline{w_{\text{A}}^2}\right)}^{\frac{1}{2}}\right]}^2/2S_0$$ (1)

For anticorrelated motion, the corrected distance is:

$$\bar{S}=S_0+{\left[{\left(\overline{w_{\text{B}}^2}\right)}^{\frac{1}{2}}+{\left(\overline{w_{\text{A}}^2}\right)}^{\frac{1}{2}}\right]}^2/2S_0$$ (2)

If the motion between atoms is considered to be noncorrelated, the corrected distance is calculated as follows:

$$\bar{S}=S_0+\left(\overline{w_{\text{A}}^2}+\overline{w_{\text{B}}^2}\right)/2S_0$$ (3)

In Eqs. (1), (2), and (3), $\bar{S}$ is the corrected distance, S₀ is the distance between average positions obtained from the X-ray experiment, and $\overline{w^2}$ is the average of the square of the projected instantaneous displacements w of the two atoms that can be linked to isotropic B-factors (B):

$$\overline{w^2}=\frac{B}{4{\pi }^2}$$ (4)

Selection of X-ray structures and atomic pairs for calculations

A total of 4774 protein X-ray structures used for calculations were downloaded from the Research Collaboratory for Structural Bioinformatics PDB on May 11, 2009 using the following search criteria: structures had to be solved by X-ray crystallography with a resolution of ≤ 2.5 Å and with a refinement R_free factor lower than 0.2, and no structures with nonphysical negative B-factors were allowed. The criteria for the selection of atomic pairs used for analysis were as follows: they had to be separated by at least five amino acids if they belonged to the same chain, and the distance between them had to be smaller than 5 Å and larger than 80% of the sum of their van der Waals radii.

MD simulations

Five independent 20-ns MD trajectories of a single-unit cell of each protein crystal (villin headpiece, ubiquitin, and SH3 domain) were generated using the GROMOS 45A3 force field.⁴⁵ The starting structures for the simulations were obtained by performing P2₁2₁2₁ symmetry operation on an experimental X-ray structure of each protein (villin headpiece, PDB ID: 2RJY; ubiquitin, PDB ID: 1UBI; SH3 domain, PDB ID: 1SHG)^25,26,35,46 to account for the fact that each of the unit cells contains four symmetry-related molecules. The simulation boxes had the following experimental dimensions: villin headpiece, 31.21 Å, 37.78 Å, and 53.15 Å; ubiquitin, 50.84 Å, 42.77 Å, and 28.95 Å; and SH3 domain, 34.00 Å, 42.27 Å, and 49.85 Å, containing four proteins each. The boxes were solvated with 328/324/0 SPC⁴⁷ waters placed in crystallographically identified sites and with 540/276/1153 SPC water molecules placed at noncrystallographic sites for the villin headpiece, ubiquitin, and SH3 domain, respectively. Further simulation details can be found in Supplementary Data.

Calculations of average interatomic separations

The last 15 ns of each simulated trajectory were included in the calculations, and each frame was separated into four different structures from the unit cell of each protein (villin headpiece, ubiquitin, and SH3 domain). The backbone of every structure was aligned to the reference structure (PDB IDs: 2RJY, 1UBI, and 1SHG) by using the McLachlan algorithm,⁴⁸ as implemented in ProFit version 3.1^†, but excluding the unstructured tail of ubiquitin (residues 71–76) from alignment (it was included in all the other analyses). The choice of the reference structure for the alignment in these cases has a minor effect on the root-mean-square deviations (RMSDs) and RMSFs, as shown by our previous work.⁴⁹ The average structure was calculated from the aligned structures and used to select atomic pairs for the calculations based on the criteria listed in Selection of X-ray Structures and Atomic Pairs for Calculations. Before the application of the equations for calculating corrections, B-factors were derived from RMSFs obtained for the aligned structures (Eq. (5)). For each atomic pair, we calculated the corrections, assuming different types of motion, as well as the instantaneous distances, which were then averaged accordingly:

$$B_i=\frac{8{\pi }^2}{3}{\text{RMSF}}_i^2$$ (5)

X-ray refinement details

Crystallographic refinement was performed with Refmac5 version 5.6.0081⁵⁰ using the original data deposited for the 2RJY, 1H8K, and 3EFU structures of the villin headpiece, SH3 domain, and ubiquitin, respectively. Twenty-five cycles of refinement were performed for each of the test cases using default values for all other parameters, including automated weighting between geometry and X-ray target functions. The only difference between restrained and unrestrained refinements is the specification of the distance restraints, with equal weights given to all distances. The molecular replacement solutions were determined using the program MOLREP;⁵¹ unfortunately, molecular replacement could not be performed on test case 2RYJ, as the molecular replacement solution was not available in the PDB.

The following are the supplementary materials related to this article.

Supplementary data

Edited by I. Wilson