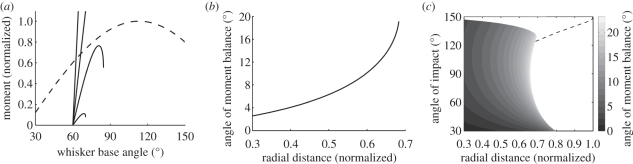
Figure 3.
The balance of moments method is based on how radial distance relates to how much the vibrissa rotates beyond initial impact. (a) For a given contact angle (60° shown here) and given radial distance (30, 50, 70 and 90% vibrissa length shown here), the angle of moment balance is defined as the maximum change in θ beyond initial impact (where the curves intersect). (b) The relationship between angle of moment balance and radial distance (for any given angle of impact) is monotonic, allowing the determination of radial distance. (c) Repeating these steps for a range of impact angles, we obtain a surface. The curve in (b) can be interpreted as a horizontal slice through the surface at θi = 60°. The white space below the dashed line indicates situations where the vibrissa flicked past the object, and the space above the line indicates where moment balance was not achieved owing to the limited range of whisking motion.