Abstract
Purpose: A new model is introduced that individually resolves the delivery, transport, and phosphorylation steps of metabolism of glucose and its analogs in skeletal muscle by interpreting dynamic positron emission tomography (PET) data.Methods: The model uniquely utilizes information obtained from the competition between glucose and its radiolabeled analogs. Importantly, the model avoids use of a lumped constant which may depend on physiological state. Four basic physiologic quantities constitute our model parameters, including the fraction of total tissue space occupied by interstitial space (fIS), a flow-extraction product and interstitial (ISg) and intracellular (ICg) glucose concentrations. Using the values of these parameters, cellular influx (CI) and efflux (CE) of glucose, glucose phosphorylation rate (PR), and maximal transport (VG) and phosphorylation capacities (VH) can all be determined. Herein, the theoretical derivation of our model is addressed and characterizes its properties via simulation. Specifically, the model performance is evaluated by simulation of basal and euglycemic hyperinsulinemic (EH) conditions.Results: In fitting the model-generated, synthetic data (including noise), mean estimates of all but ICg of the parameter values are within 5% of their values for both conditions. In addition, mean errors of CI, PR, and VG are less than 5% whereas those of VH and CE are not.Conclusions: It is concluded that under the conditions tested, the novel model can provide accurate parameter estimates and physiological quantities, except ICg and two quantities that are dependent on ICg, namely CE and VH. However, the ability to estimate ICg seems to improve with increases in intracellular glucose concentrations as evidenced by comparing ICg estimates under basal vs EH conditions.
Keywords: glucose transport, radiopharmaceutical, PET, glucose clamp
INTRODUCTION
In positron emission tomography (PET), the glucose analog labeled with the radionuclide 18F, 2-fluoro-2-deoxy-D-glucose ([18F]2FDG), is widely used to study glucose metabolism, especially in brain. It is well known that the uptake of glucose and its analogs, such as [18F]2FDG, from plasma to brain utilize glucose transporters, primarily GLUT1, to cross the blood-brain barrier. Once inside the cell, [18F]2FDG is phosphorylated by hexokinase forming [18F]FDG-6-phosphate, which is trapped intracellularly. To probe these processes, two-compartment models with three (3K model) and four (4K model) rate constants were proposed by Sokoloff et al.1 and Phelps et al.,2 respectively. Both models lump extracellular and intracellular glucose into a single compartment and therefore cannot resolve the transport step.
Herein, our emphasis is on glucose handling by skeletal muscle which, because of its overall mass, is one of the largest consumers of glucose in the body and is the target of some pharmaceuticals used to treat diabetes. The application of the above-mentioned 3K and 4K models to skeletal muscle is controversial.3 Unlike brain, skeletal muscle does not have a tight barrier between capillary and interstitial space. In skeletal muscle, glucose diffuses into interstitial space from plasma through pores and fenestrations between endothelial cells in capillaries. Glucose then enters cells via facilitative glucose transporters, GLUT1 and GLUT4, with GLUT4 being dominant in mediating the glucose transport response to insulin. Once inside the cell, glucose phosphorylation is catalyzed by hexokinase. Since the 3K and 4K models lump extracellular and intracellular glucose into the same compartment, these models cannot independently account for glucose transport from plasma into cells. Consequently, a three-compartment five-rate-constant model (5K model) was proposed by Bertoldo et al.3 that resolves glucose metabolism into three individual steps: delivery, transport, and phosphorylation. While the level of detail is an important advantage of this 5K model, it is challenging to reliably determine values for all of the model’s parameters.
To this end, Bertoldo and co-workers have used sequential injections of the nonphosphorylatable glucose analog 11C-labeled 3-O-methyl-D-glucose [11C]3OMG) and the phosphorylatable analog [18F]2FDG to obtain more information than can be obtained with only a single injection.4 They endeavored to more reliably resolve the transport and phosphorylation steps. This approach seems appropriate, yet challenges remain: First, [11C]3OMG, a reference tracer for glucose transport in PET has a limitation in its clinical use due to the 20-min half-life of 11C. Second, a value for a lumped constant (LC) must be assumed so that one may infer the glucose metabolic rate from that of the analog, whereas the value depends on plasma and tissue glucose concentrations.5, 6 Third, the 5K model3 has five parameters (i.e., five rate constants), which make their reliable estimation difficult. Fourth, no direct estimation of the interstitial and intracellular glucose concentrations is provided by this 5K or any other published PET glucose model.
Herein, we address these challenges. We use a nonphosphorylatable analog 18F-labeled 6-fluoro-6-deoxy-D-glucose [18F]6FDG), which has a 110-min half-life and has been shown to be transported but not phosphorylated.7 We propose a novel model that resolves delivery, transport, and phosphorylation steps and which explicitly accounts for interactions between glucose and its analog thereby obviating the need for a lumped constant. Our proposed model incorporates physiologic constraints and well-established kinetic laws and requires four independent parameters to be estimated from the PET data.
We first introduce the theoretical derivation of our model and present studies characterizing its ability to estimate parameter values in computer simulations wherein the estimates can be compared to the known true values. We then design a two-injection protocol for PET scanning. The experimental procedure utilizes PET scanning upon injection of [18F]6FDG followed by a subsequent injection of [18F]2FDG with continued scanning. This two-injection simulation protocol is performed for both basal (fasting) and euglycemic hyperinsulinemic (EH) conditions.
METHODS AND MATERIALS
Kinetic modeling of glucose analogs in skeletal muscle
Similar to the 5K model, our model has three compartments with five rate constants. Molar concentrations of the glucose analog in the arterial plasma, interstitial, and intracellular spaces are denoted Pa, ISa, and ICa, respectively, and the intracellular concentration of the phosphorylated analog denoted IPa is assumed to be metabolically trapped inside the cell. In this model, total tissue space (Vtotal) is the sum of interstitial (VIS), intracellular (VIC), and blood (Vb) spaces. From the molar balance, the following equations define the quantitative relationship for the kinetic model:
| (1) |
| (2) |
| (3) |
Based on the assumptions that the interstitial space is a well-mixed compartment and that capillaries in the tissue are uniformly distributed, Johnson and Wilson8 showed that when the intracapillary solute concentrations equilibrate rapidly compared with the interstitial solute concentrations, the flow-extraction product (FE, ml/min) can be used to describe the transcapillary flux of solutes from plasma to interstitial space. In addition, Renkin9 showed that when solutes cross the capillary wall primarily by diffusion, the first term of the right side of Eq. 1, i.e., FE[Pa(t)-ISa(t)], can be used to quantify the exchange of solutes, e.g., glucose analogs, between plasma and interstitial space. The rate constants k3a and k4a denote transport of glucose analogs by glucose transporters. Inside the cell, the rate constant k5a describes the phosphorylation of glucose analogs catalyzed by hexokinase.
Now, we can normalize Eqs. 1, 2, 3 by total tissue space (Vtotal).
| (4) |
| (5) |
| (6) |
where fIS = VIS/Vtotal, fIC = VIC/Vtotal, k1 = FE/Vtotal, and k2 = k1/fIS. Herein, we assume that glucose and its analogs have the same rate constant k1(= FE/Vtotal) because they are carried by blood flow (F) and have similar extraction (E). Since we define k2 = k1/fIS, the rate constant k2 is the same for glucose and its analogs. To derive the final model equations for parameter estimates, we define IS′a(t) = fISISa(t), IC′a(t) = fICICa(t), and IP′a(t) = fICIPa(t). As a result, Eqs. 4, 5, 6 can be written as
| (7) |
| (8) |
| (9) |
Now, as shown in Fig. 1, our model can be described by Eqs. 7, 8, 9, which are the final model equations used for parameter estimates.
Figure 1.
Kinetic model for glucose analogs.
PET images pixel values are calibrated to the total radioactivity concentration, which is calculated by multiplying molar concentration by specific activity and summing activities in all compartments:
| (10) |
where B(t) is the decay-corrected whole blood activity, and fb (=Vb/Vtotal) is the fraction of total tissue space occupied by blood space. Integration over time and division by frame duration yields the time-averaged value between the beginning and ending time of frame i. A is the specific activity in units of activity per quantity (μCi/pmol). According to Eqs. 7, 8, 9, 10, six model parameters are k1, fIS, k3a, k4a, k5a, and fb. In Sec. 2B, we would show that the rate constants k3a, k4a, and k5a can be expressed in terms of k1, fIS, ISg, and ICg and that the final model parameters to be estimated are k1, fIS, ISg, and ICg.
Classic Michaelis–Menten kinetics
Using classic enzyme-substrate kinetics, a glucose analog is modeled as a competitive inhibitor of glucose transport and phosphorylation. Consequently, the reaction velocity Va, of either process, for substrate (glucose analog) at concentration Sa can be expressed as Va = Vmax × (Sa/Ka)/[1+Sa/Ka+Sg/Kg], where Vmax is the maximum velocity, Ka is the Michaelis constant for the analog, Kg is the Michaelis constant for glucose, and Sg is the concentration of glucose.10 Generally speaking, the concentration of radiolabeled glucose analog in a PET study is much less than its Michaelis constant so that Sa/Ka is small compared to one and may be neglected in the denominator. With this simplification, substituting the appropriate interstitial or intracellular concentration for substrate concentration Sa into this velocity expression, and dividing by Sa, we obtain the effective rate “constants” k3a and k4a for transport and k5a for phosphorylation of the glucose analog
| (11) |
| (12) |
| (13) |
We use the symbols V to denote maximum velocities in units of millimole per minute per milliliter tissue and K to denote Michaelis constants. Superscripts G and H denote glucose transporter and hexokinase, respectively. Subscripts a and g denote glucose analog and glucose, respectively. ISg, (millimole per milliliter interstitial space) and ICg (millimole per milliliter intracellular space) are, respectively, the interstitial and intracellular concentrations of glucose. Based on the assumption that glucose transport is bidirectional and symmetric, Michaelis constants for the forward and reverse transport are equal11 and the units of and are millimoles per mililiter of distribution volume, which are interstitial and intracellular spaces for influx and efflux, respectively. In the right side of Eq. 11, the units in the numerator are millimoles per minute per milliliter tissue, the units within the parentheses in the denominator are millimoles per mililiter interstitial space, and the unit of fIS in the denominator is milliliter interstitial space per milliliter tissue so that k3a has the expected units of per minute. Analogously, in the right sides of Eqs. 12, 13 the units in the numerators are millimoles per minute per milliliter tissue, the units in the parentheses of the denominators are millimoles per milliliter intracellular space, and fIC has units of milliliter intracellular space per milliliter tissue so that k4a and k5a have units of per minute. Note that the rate constant k5a is only pertinent to glucose or its analogs that can be phosphorylated. From Eqs. 11, 12, 13, it is clear that values of k3a, k4a, and k5a depend on ISg and ICg and thus are not actually constants. However, if PET studies are performed when glucose concentrations are stable, k3a, k4a, and k5a may be treated as constants during the studies. Michaelis constants for glucose and its analogs are assumed to be fixed values under most physiological conditions and will be determined separately via transporter assays. Now, given assumed Michaelis constants (i.e., , , , and ), model parameters are k1, fIS, fIC, fb, , , ISg, and ICg. As detailed below, physiologic constraints are applied so that the final model parameters are k1, fIS, ISg, and ICg.
PET studies are performed with steady glucose concentrations. Accordingly, the left sides of differential equations for glucose—analogous to Eqs. 4, 5 with replacement of subscripts a by g in all symbols to denote glucose—equate to zero and the differential equations simplify to algebraic equations
| (14) |
| (15) |
In addition, plasma (Pg), interstitial (ISg), and intracellular (ICg) glucose concentrations are assumed to be constant over the time-course of PET studies. The rate constant expressions k3g, k4g, and k5g for glucose are obtained from those of its analog Eqs. 11, 12, 13, 14 by replacing the values of maximum velocities and Michaelis constants of the analog with those of glucose. Thus, rate constant k3g, k4g, and k5g can be written as
| (16) |
| (17) |
| (18) |
After substituting Eqs. 16, 17, 18 into the steady-state equations for glucose Eqs. 14, 15, one has
| (19) |
| (20) |
Solving Eq. 19 for , one has
| (21) |
According to Eq. 19, we know that k1(Pg-ISg) = ISg/( + ISg)- ICg/( + ICg) and then Eq. 20 can be written as
| (22) |
Solving Eq. 22 for , one has
| (23) |
Since glucose and its analogs have similar molecular weights and chemical properties and are acted upon by the same transporter, we assume that as have others for GLUT1.12, 13, 14 We assume the case to be analogous for GLUT4. Thus, for simplicity, we denote and as VG. The analogous assumption, i.e. , is applied for hexokinase so we, likewise, denote and by VH. After substituting Eqs. 21, 23 into Eqs. 11, 12, 13, the rate constants k3a, k4a, and k5a are
| (24) |
| (25) |
| (26) |
Since blood space (Vb) in skeletal muscle is relatively small as compared to VIS and VIC,15 we assume that Vtotal ≈ VIS + VIC. As a result, fIC = VIC/Vtotal ≈ 1-fIS, for skeletal muscle. Thus, given measured Pg and assumed Michaelis constants, the rate constants k3a, k4a, and k5a can be expressed in terms of k1,fIS,ISg, and ICg. The assumption also indicates that fb × B(t) in Eq. 10 may be ignored. At the end of Sec. 2A, six parameters to be estimated are k1, fIS, k3a, k4a, k5a, and fb. With these simplifications, the final model parameters are k1, fIS, ISg, and ICg. These are a priori locally identifiable (see Appendix A).16
Classic Simulations of PET data in rat skeletal muscle
PET simulations were performed using COMKAT.17, 18 Using Eq. 10, synthetic data without including radioactive decay were generated with a plasma input (Pa) function defined as
| (27) |
with A1 = 800, A2 = 3, A3 = 2 pmol/ml; L1 = 20, L2 = 0.6, and L3 = 0.01 min−1 for 6FDG and A1 = 1500, A2 = 24, A3 = 6 pmol/ml; L1 = 16, L2 = 1.2, and L3 = 0.03 min−1 for 2FDG under basal conditions.19 (Note that in [18F]2FDG and [18F]6FDG prepared for PET studies, the amount of labeled analog is negligible as compared to amount of unlabeled 2FDG and 6FDG, respectively.) In practice, EH conditions would have lower concentration of 2FDG (or 6FDG) in plasma than basal conditions because the muscular uptake of glucose and its analog is increased by insulin. Thus, we increase the values of L1, L2, and L3 of 2FDG and 6FDG by 25% for EH conditions.
Based on the published data,3, 15 the fraction of the total tissue space occupied by the blood space (fb = Vb/Vtotal) is negligible in rat skeletal muscle. Thus, we assume that skeletal muscle has 75% intracellular space (fIC), 25% interstitial space (fIS) and neglect fb. The value of the Michaelis constant for glucose transport is set to 3.5 mM (Ref. 20) and that of phosphorylation by hexokinase is set to 0.13 mM.21 As the Michaelis constant for 6FDG transport () has not yet been determined, we made a preliminary estimate of 10 mM based on published22 and unpublished experimental data. Also, we assume that the Michaelis constant of 2FDG transport () is 8 mM based on unpublished experimental data and that of phosphorylation by hexokinase equals 0.17 mM.21
For both basal and EH conditions, plasma glucose concentration (Pg) was set to 6 mM, consistent with our prior experimental data in the rat.22 ISg was specified as 85% of Pg (=5.1 mM) and 50% of Pg (=3 mM) for basal and EH conditions, respectively.19 From the skeletal muscle blood flow in rats,23 we assume k1 = 0.04 min−1 for basal conditions. In rat skeletal muscle, fasting intracellular free glucose concentration (ICg) is close to zero20 so that ICg is set to 0.05 mM for basal conditions. Given these values, we solved Eqs. 21, 23 to obtain values of VG (=0.06 mmol/min/ml tissue) and VH (=0.13 mmol/min/ml tissue). For EH conditions, wherein insulin brings transporters to the plasma membrane and stimulates phosphorylation, we increased the number of transporters (VG) 5-fold24 and hexokinase activity (VH) 2-fold25 and set ISg = 3 mM. Given these values, we solved Eqs. 21, 23 to obtain values for k1 and ICg. Interestingly, this indicates a 1.1-fold increase in k1. Physiologically, this could be interpreted as an increase in blood flow.26, 27 Table TABLE I. is the summary of values of parameters used for both conditions.
Table 1.
Summary of parameters used in basal and EH conditions.
| Symbol | Description | Value for basal conditions | Value for EH conditions | Unit |
|---|---|---|---|---|
| k1 | Rate constant of diffusion of glucose and its analogs from plasma to interstitial space | 0.040 | 0.044 | ml/ml per min |
| ISg | Interstitial glucose concentration | 5.1 | 3.0 | mmol/ml IS space |
| ICg | Intracellular glucose concentration | 0.050 | 0.135 | mmol/ml IC space |
| VG | Maximal transport capacity | 0.06 | 0.31 | mmol/min/ml tissue |
| VH | Maximal phosphorylation capacity | 0.13 | 0.26 | mmol/min/ml tissue |
| Michaelis constant for glucose transport by GLUT4 | 3.5 | 3.5 | mM | |
| Michaelis constant for 2FDG transport by GLUT4 | 8 | 8 | mM | |
| Michaelis constant for 6FDG transport by GLUT4 | 10 | 10 | mM | |
| Michaelis constant for phosphorylation of glucose | 0.13 | 0.13 | mM | |
| Michaelis constant for phosphorylation of 2FDG | 0.17 | 0.17 | mM | |
| CI | Cellular influx | 0.0369 | 0.1435 | mmol/min/ml tissue |
| CE | Cellular efflux | 0.0009 | 0.0115 | mmol/min/ml tissue |
| PR | Phosphorylation rate | 0.0360 | 0.1320 | mmol/min/ml tissue |
With parameter values assigned above, we generated model output and treated it as simulated, noiseless PET data. To this we added simulated noise according to
| (28) |
where and Di are, respectively, the noisy and the noiseless data at the ith frame. indicates deviates from a normal distribution with zero mean and variance . Standard deviation (SD) was set as
| (29) |
where α is the noise level.28 Parameter values were estimated by minimizing the weighted least squares objective function
| (30) |
where p is the parameter vector (k1, fIS, ISg, and ICg), wi is the weight for frame i, and CPET,i is the model output in frame i. In this simulation, we used the known SD to determine the weights wi () for fitting data. With the experimental data, we would use either the iteratively reweighted least squares or extended least squares methods to estimate the noise and to determine weights.28 The data-fitting algorithm was performed with COMKAT’s fit function that currently uses matlab 2010 b (The Mathworks, Inc., Natick, MA) function ‘‘lsqcurvefit,’’ a trust-region-reflective method.29 In addition, data from both injections were considered as a single large set that was fit contemporaneously. In particular, model output [i.e., Eq. 10] was calculated by summing the radioactivity from the two radiopharmaceuticals. We repeated this minimization 500 times producing 500 sets of parameter estimates, one set for each of 500 simulated, noisy data sets. This entire process was performed twice: during basal and EH conditions. For both basal and EH conditions, initial guesses for k1, ISg, ICg, and fIS were 0.1 min−1, 4.0 mM, 0.1 mM, and 0.15, and the bounds were set as 0.001 ≤ k1 ≤ 0.5 min−1, 2 ≤ ISg ≤ 6 mM, 0.001 ≤ ICg ≤ 0.5 mM and 0.1 ≤ fIS ≤ 0.5. Means and standard deviations (SD) of the parameter estimates were calculated from estimates obtained by fitting the 500 data sets. Also, bias and precision were summarized using mean ±SD of estimation errors [estimation error = (estimated value − true value)/true value × 100%]. Cellular influx (CI), efflux (CE), and phosphorylation rate (PR) of glucose can be determined as
| (31) |
| (32) |
| (33) |
In skeletal muscle, upon cellular entry glucose is phosphorylated by hexokinase and further metabolized. Since muscle lacks glucose-6-phosphatase, glucose-6-phosphate cannot be dephosphorylated and exit the cells. Consequently, PR is equal to glucose metabolic rate,30 the usual outcome measurement of the 3K and 4K models used with [18F]2FDG data.
The simulated experimental protocol included a 1-h PET scan beginning with a bolus injection of [18F]6FDG (t = 0 min) and then continued with another hour of PET scanning after a bolus injection of [18F]2FDG at t = 60 min. As a result, the total simulated imaging time of this two-injection protocol was fixed to 2 h. To emulate the time-sampling inherent with PET we binned the data into a sequence of 2-s (n = 6) frames followed by sequences of 6-s (n = 8), 15-s (n = 16), 60-s (n = 5) and finally 300-s (n = 10) frames. To visualize parameter estimates in terms of bias and precision, we use box plots. A gray bar shows the central 50 percentile and the horizontal black line within the box designates the median. Circles indicate outliers defined as estimates that are below the lower quartile or above the upper quartile by more than 1.5 times the difference between the upper and lower quartile.
RESULTS
Model behaviors under basal and EH conditions
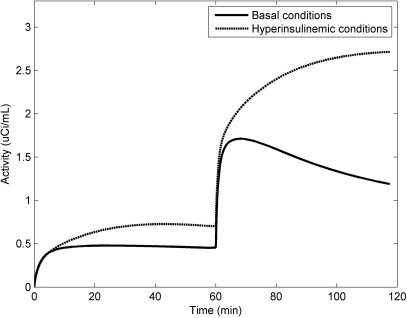
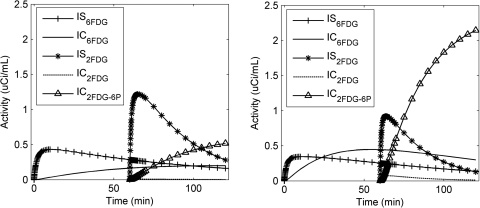
Noise-free time-activity curves (TACs) under both conditions are shown in Fig. 2. As compared to basal conditions, EH conditions cause an increase in the later tissue radioactivity for [18F]6FDG, which is consistent with our previous [18F]6FDG studies.22 For [18F]2FDG, the later tissue radioactivity increases with time under EH conditions, but decreases under basal conditions. To explain the different curve shapes of these two conditions, we plot the model-predicted radioactivity for each compartment in Fig. 3. In contrast to basal conditions, EH conditions have lower interstitial [18F]6FDG (IS6FDG) but higher intracellular [18F]6FDG (IC6FDG), which is attributed to an insulin-stimulated increase in the number of glucose transporters. Thus, EH conditions show higher tissue radioactivities for [18F]6FDG. Also, similar effects are observed for [18F]2FDG. But the difference is greater since once [18F]2FDG enters the cell, it is rapidly phosphorylated. Upon entry, intracellular [18F]2FDG (IC2FDG) is immediately phosphorylated into [18F]2FDG-6-P (IP2FDG-6-P) by hexokinase and trapped inside cells. This causes rapid accumulation of IP2FDG-6-P under EH conditions compared to basal conditions, as expected. As a result, the tissue radioactivities after the injection of [18F]2FDG keeps increasing under EH conditions, but promptly decreases under basal conditions.
Figure 2.
Noise-free tissue TACs after injecting a bolus of [18F]6FDG and [18F]2FDG at 0 and 60 min, respectively, under basal and EH conditions.
Figure 3.
Resolution of tissue radioactivities in each of three compartments after injection a bolus of [18F]6FDG and [18F]2FDG at 0 and 60 min, respectively, under basal (left) and EH (right) conditions.
With corresponding parameters specified above, we determined CI, CE, and PR of glucose under basal and EH conditions, Table TABLE I.. At the basal state, CI is almost the same with PR but CE is much lower than CI and PR indicating that virtually all the glucose that enters the cell is phosphorylated and then further metabolized. In the insulin-stimulated state, the increases over basal conditions are CI: 0.1435, CE: 0.0115, and PR: 0.1320 mmol/min/ml tissue. This shows that synthetic data set exhibits reasonable physiologic behavior: at the basal state, the transport step is rate-limiting and hexokinase phosphorylates glucose essentially as fast as it is transported into cells whereas with insulin stimulation the phosphorylation step becomes more rate-determining.31, 32
Summary of model fits and parameter estimates
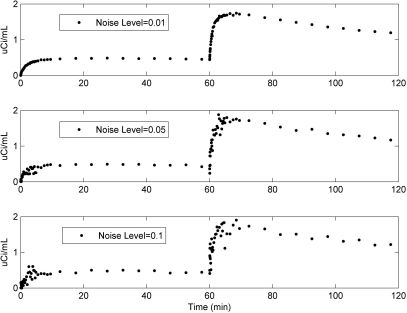
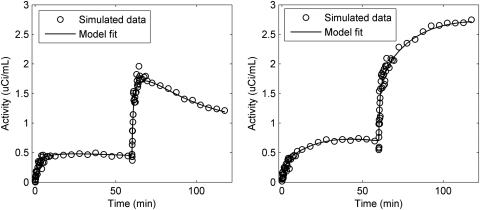
Figure 4 shows TACs at different noise levels (α = 0.01, 0.05, and 0.1) under basal conditions. The noise level α = 0.05 best agreed with our prior experimental data (see Appendix B).22 Example fits (noise level α = 0.05) are shown in Fig. 5 for basal (left) and EH (right) conditions. Our model appears to fit the synthetic data well for both conditions noting the expected high variability in the data in early frames due to their short duration. In particular, the model parameters can generally be estimated. When the noise level α = 0.05 was used for simulations, the results showed that in both basal and EH conditions, mean errors (i.e., biases) of the parameter values were ≤5% with SD (i.e., precision) <10% for k1, ISg, fIS, VG, CI, and PR. However, under basal conditions, ICg (163 ± 322%), CE (159 ± 312%) and VH (271 ± 757%) show poor estimates (mean errors ± SD). Except VH: 645 ± 1559%, the other two parameters were better determined in the EH condition, ICg: 37 ± 115% and CE: 41 ± 119%, than in the basal condition.
Figure 4.
Model-predicted [18F]6FDG (i.e., 0–60 min) and [18F]2FDG (i.e., 60–120 min) time-activity curves during basal conditions at noise levels of 0.01, 0.05, and 0.1.
Figure 5.
Simulation data set (noise levels = 0.05) and model fit during basal (left) and EH (right) conditions.
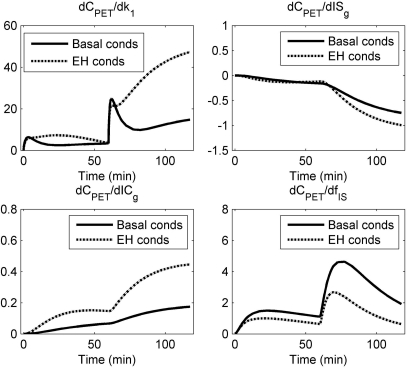
To investigate the identifiability of each model parameter, the sensitivity functions, which are derivatives of model output with respect to the change of each parameter, for basal and EH conditions were evaluated in Fig. 6. In terms of curve shape, the sensitivity functions are different for different parameters. For a given parameter, the curve shapes are similar both in basal and EH conditions. From the magnitude, the value of the sensitivity function for ICg is much less than that of the other parameters, which indicates that the data are relatively insensitive to ICg. Thus, the estimates of ICg with high bias and low precision are not surprising.
Figure 6.
Sensitivity functions under basal and hyperinsulinemic conditions. For both conditions, the magnitude of dCPET/(dICg) is low. This means that ICg is insensitive to measured data.
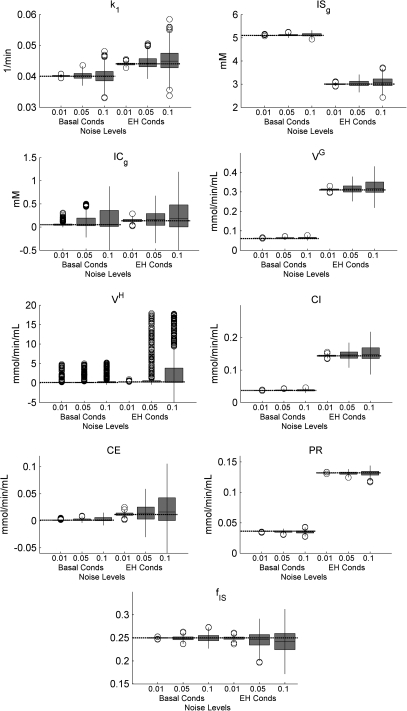
The distributions of parameter estimates of 500 trials obtained from both conditions at different noise levels (α = 0.01, 0.05, and 0.1) were shown graphically in box plots, Fig. 7. Means and standard deviations of model parameters and individual rate constants for basal and EH conditions are tabulated in Tables 2, TABLE SII. (see Appendix C), respectively. In addition, the summary of bias and precision of all parameters (Table TABLE SIII.) for both basal and EH conditions is included in Appendix C. As noise levels are decreased, parameter estimates improve, especially for ICg, CE, and VH. For EH conditions, the number of outliers for VH decreases as the noise level reduces to 0.01. For basal conditions, the box plot of VH shows many outliers at each noise level, but PR which relates to VH shows good precision with few outliers. At the highest noise level, the bias of ICg, CE, and VH exceeds 100% of its true value, but other parameters are estimated with a bias of less than 6%, indicating much less sensitivity to noise.
Figure 7.
The distribution of the parameter estimates is summarized by box plots for different noise levels (α = 0.01, 0.05, and 0.1) under EH conditions. The gray bars denote the central 50 percentile, the black lines denote the median, the circles denote outliers, and the horizontal dashed lines denote the true values. The parameter estimates are well-behaved in that they converge toward the true value with diminishing noise level.
Table 2.
Summary of parameter estimates for basal conditions.
| Noise levels | 0.01 | 0.05 | 0.1 | |
|---|---|---|---|---|
| Parameters | True | 500 sets of estimates (mean ± SD) | ||
| k1 (mL/mL min−1) | 0.04 | 0.04 ± 0.00 | 0.04 ± 0.00 | 0.04 ± 0.00 |
| ISg (mM) | 5.10 | 5.10 ± 0.01 | 5.12 ± 0.04 | 5.13 ± 0.07 |
| ICg (mM) | 0.05 | 0.06 ± 0.05 | 0.13 ± 0.16 | 0.16 ± 0.20 |
| fIS (unitless) | 0.25 | 0.25 ± 0.00 | 0.25 ± 0.00 | 0.25 ± 0.01 |
| VG (mmol/min/mL tissue) | 0.06 | 0.06 ± 0.00 | 0.06 ± 0.00 | 0.06 ± 0.00 |
| VH (mmol/min/mL tissue) | 0.13 | 0.39 ± 0.82 | 0.48 ± 0.98 | 0.65 ± 1.20 |
| CI (mmol/min/mL tissue) | 0.0369 | 0.0370 ± 0.0005 | 0.0377 ± 0.0017 | 0.0377 ± 0.0028 |
| CE (mmol/min/mL tissue) | 0.0009 | 0.0009 ± 0.0008 | 0.0023 ± 0.0027 | 0.0028 ± 0.0033 |
| PR (mmol/min/mL tissue) | 0.0360 | 0.0360 ± 0.0004 | 0.0354 ± 0.0018 | 0.0349 ± 0.0027 |
| k2 (min−1) | 0.16 | 0.16 ± 0.00 | 0.16 ± 0.01 | 0.16 ± 0.01 |
| k3_6FDG (min−1) | 0.0101 | 0.0102 ± 0.0001 | 0.0104 ± 0.0001 | 0.0103 ± 0.0011 |
| k4_6FDG(min−1) | 0.0082 | 0.0082 ± 0.0001 | 0.0081 ± 0.0002 | 0.0081 ± 0.0004 |
| k3_2FDG(min−1) | 0.0127 | 0.0127 ± 0.0002 | 0.0130 ± 0.0007 | 0.0129 ± 0.0013 |
| k4_2FDG(min−1) | 0.0102 | 0.0102 ± 0.0001 | 0.0102 ± 0.0003 | 0.0101 ± 0.0005 |
| k5_2FDG(min−1) | 0.7341 | 2.79 ± 6.43 | 3.49 ± 7.68 | 4.83 ± 9.40 |
Table 3.
Summary of parameter estimates for EH conditions.
| Noise levels | 0.01 | 0.05 | 0.1 | |
|---|---|---|---|---|
| Parameters | True | 500 sets of estimates (mean ± SD) | ||
| k1 (mL/mL min−1) | 0.044 | 0.04 ± 0.00 | 0.04 ± 0.00 | 0.05 ± 0.00 |
| ISg (mM) | 3.00 | 3.00 ± 0.04 | 3.04 ± 0.13 | 3.08 ± 0.20 |
| ICg (mM) | 0.13 | 0.14 ± 0.04 | 0.19 ± 0.15 | 0.22 ± 0.20 |
| fIS (unitless) | 0.25 | 0.25 ± 0.00 | 0.24 ± 0.02 | 0.24 ± 0.02 |
| VG (mmol/min/mL tissue) | 0.31 | 0.31 ± 0.00 | 0.32 ± 0.02 | 0.32 ± 0.03 |
| VH (mmol/min/mL tissue) | 0.26 | 0.26 ± 0.06 | 1.93 ± 4.04 | 3.04 ± 5.07 |
| CI (mmol/min/mL tissue) | 0.1435 | 0.1441 ± 0.0029 | 0.1477 ± 0.0124 | 0.1511 ± 0.0166 |
| CE (mmol/min/mL tissue) | 0.0115 | 0.0123 ± 0.0032 | 0.0162 ± 0.0138 | 0.0198 ± 0.0183 |
| PR (mmol/min/mL tissue) | 0.1320 | 0.1380 ± 0.0005 | 0.1315 ± 0.0024 | 0.1313 ± 0.0183 |
| k2 (min−1) | 0.176 | 0.177 ± 0.004 | 0.183 ± 0.020 | 0.019 ± 0.033 |
| k3_6FDG (min−1) | 0.0670 | 0.0673 ± 0.0017 | 0.0699 ± 0.0077 | 0.0719 ± 0.0109 |
| k4_6FDG(min−1) | 0.0399 | 0.0399 ± 0.0001 | 0.0399 ± 0.0004 | 0.0399 ± 0.0008 |
| k3_2FDG(min−1) | 0.0837 | 0.0842 ± 0.0021 | 0.0874 ± 0.0096 | 0.0898 ± 0.0136 |
| k4_2FDG(min−1) | 0.0499 | 0.0499 ± 0.0001 | 0.0499 ± 0.0005 | 0.0499 ± 0.0010 |
| k5_2FDG(min−1) | 0.9977 | 1.0330 ± 0.4488 | 14.31 ± 32.14 | 23.08 ± 40.27 |
Table 4.
Summary of bias and precision for both basal and EH conditions at different noise levels.
| 500 sets of parameter estimates | ||||||
|---|---|---|---|---|---|---|
| Conditions | Basal | EH | ||||
| Noise levels | 0.01 | 0.05 | 0.1 | 0.01 | 0.05 | 0.1 |
| Parameters | Error %(mean ± SD) | |||||
| k1 | 0.27 ± 0.60 | 0.32 ± 2.81 | 0.30 ± 5.90 | −0.02 ± 0.96 | 1.05 ± 4.48 | 2.79 ± 8.36 |
| ISg | 0.05 ± 0.22 | 0.34 ± 0.86 | 0.57 ± 1.30 | 0.13 ± 1.04 | 1.24 ± 4.41 | 2.74 ± 6.81 |
| ICg | 16 ± 90 | 163 ± 322 | 228 ± 391 | 6 ± 28 | 37 ± 114 | 66 ± 152 |
| fIS | 0.03 ± 0.38 | −0.43 ± 1.76 | −0.07 ± 3.33 | −0.28 ± 1.47 | −2.05 ± 6.31 | −3.34 ± 9.38 |
| VG | 0.30 ± 1.20 | 2.03 ± 4.51 | 1.91 ± 7.59 | 0.29 ± 1.53 | 2.17 ± 6.45 | 3.67 ± 8.63 |
| VH | 202 ± 632 | 271 ± 757 | 402 ± 926 | 1.63 ± 21.81 | 645 ± 1559 | 1082 ± 1956 |
| CI | 0.32 ± 1.26 | 2.17 ± 4.65 | 2.14 ± 7.63 | 0.36 ± 2.04 | 2.92 ± 8.62 | 5.27 ± 11.59 |
| CE | 16 ± 90 | 159 ± 312 | 219 ± 379 | 6 ± 28 | 40 ± 119 | 72 ± 159 |
| PR | 0.03 ± 1.22 | −1.61 ± 4.97 | −3.11 ± 7.40 | −0.15 ± 0.38 | −0.38 ± 1.84 | −0.55 ± 3.26 |
| k2 | 0.31 ± 0.85 | 0.82 ± 4.01 | 0.59 ± 8.28 | 0.29 ± 2.34 | 3.85 ± 11.06 | 8.00 ± 18.53 |
| k3_6FDG | 0.30 ± 1.47 | 2.36 ± 5.99 | 1.97 ± 10.60 | 0.54 ± 2.53 | 4.36 ± 11.50 | 7.30 ± 16.27 |
| K4_6FDG | 0.07 ± 0.63 | −0.37 ± 3.01 | −1.26 ± 5.48 | −0.03 ± 0.22 | 0.01 ± 1.06 | −0.05 ± 2.09 |
| K3_2FDG | 0.30 ± 1.47 | 2.36 ± 5.99 | 1.97 ± 10.60 | 0.54 ± 2.53 | 4.36 ± 11.50 | 7.30 ± 16.27 |
| k4_2FDG | 0.07 ± 0.63 | −0.37 ± 3.01 | −1.26 ± 5.48 | −0.03 ± 0.22 | 0.01 ± 1.06 | −0.05 ± 2.09 |
| ks_2FDG | 280 ± 875 | 375 ± 1046 | 557 ± 1281 | 3.54 ± 44.99 | 1334 ± 3221 | 2214 ± 4036 |
DISCUSSION
Model properties
Because of our physiologic-based assumptions, our model has fewer independent parameters that need to be estimated compared to other PET models that are used to assess glucose kinetics. Unique features of our model are that interstitial and intracellular glucose concentrations can be estimated directly and that the model does not use a lumped constant to relate kinetics of glucose to that of its labeled analog. We thereby avoid vagaries of using a possibly incorrect value of the lumped constant which might depend on dietary state, hormonal changes, and specifics of the tissue.5, 6 However, in this study, we have difficulties in estimates of ICg and its related quantities: CE and VH. In addition, the proposed model requires a priori knowledge of five Michaelis constants (see Table TABLE I.) which can be determined experimentally by in vitro assays. When the values of Michaelis constants derived from in vitro assays are used for in vivo studies, we may consider the effect of in vivo versus in vitro values on parameter estimates.
Our proposed model estimates transport and phosphorylation rates of glucose, and offers a direct way to quantify the rates of the individual steps of glucose metabolism in vivo. Because the method could be applied to human experiments, it can provide details about glucose metabolism on a regional or organ level in ways that heretofore have not been available. Consequently, our model could potentially provide unique insight to the evolution of diabetes, insulin resistance, and treatment of such diseases.
Model prediction
The novel model presented herein predicts responses of glucose and its analogs under various conditions. Since [18F]6FDG is not phosphorylated, a priori, we expected insulin stimulation to impact the rate at which it achieves steady state between interstitial and intracellular spaces but not to impact the steady state concentration. Importantly, the model offers a mechanistic explanation for the increase of tissue radioactivity during EH conditions that was observed with nonphosphorylated analogs both in our own prior data21 using [18F]6FDG and those of Bertoldo et al.4 using [11C]3OMG. It is well known that insulin increases the number of functional GLUT4 transporters at the plasma membrane. The capacity for glucose to enter the cell may then exceed the phosphorylation rate while the intracellular concentration increases sufficiently until mass-action increases the phosphorylation rate to balance the influx.33, 34 The increased intracellular glucose concentration increases transport competition between glucose and its radiolabeled analog for cellular efflux. Under the increased transport competition, the efflux of intracellular radiolabeled analog decreases so that tissue radioactivity increases during EH conditions.
Parameter estimates and limitations
In comparing all parameters, both conditions have relatively poor precision and high bias in estimates of ICg, CE, and VH. This may be an intrinsic limitation as physiologically ICg is too low to provide measurable competition with the analog for efflux. However, the increase of ICg from 0.05 to 0.135 mM (from basal to EH conditions) reduces mean errors from 163 to 37%. This indicates that our model would be able to obtain more accurate estimate for higher ICg. In addition, the expected improvements of parameter estimates with decreases in noise levels are evident in Fig. 7. This behavior provides evidence that the software code is being implemented correctly.
Unlike other PET models, our model does not require a LC and therefore avoids the potential for incorrect values of the LC which depends on dietary state. However, our model requires Michaelis constants of glucose and its analogs. These constants can be determined experimentally in transporter assays. Based on our analysis (see Appendix B), for example, 20% bias in slightly increases bias for ISg, (by 3 and 9% for basal and EH conditions, respectively) but has no significant effect on k1 and fIS. Incorrect values for Michaelis constants have no effect on ICg, which has high bias and low precision estimates.
Application of the new model
Insulin resistance manifested as impaired glucose transport in response to insulin is one of the hallmarks of type 2 diabetes and obesity.35 To assess insulin sensitivity, hyperinsulinemic euglycemic glucose clamp methodology has been widely used in clinical studies.36 However, this method indicates total body insulin sensitivity;37 no regional or tissue-specific information is provided. Fortunately, some earlier studies37, 38 showed that the potential of dynamic in vivo PET imaging combined with kinetic models could provide valuable information about impaired glucose metabolism in skeletal muscle. In type 2 diabetic patients, many studies35, 39 showed that the impairment of glucose phosphorylation was greater than that of glucose transport under euglycemic hyperinsulinemic glucose clamp; hence, ICg would be higher than in normal subjects. In this case, our model would perform even better than predicted herein because the poor precision was attributed to low ICg. Further studies are needed to investigate the performance of our model in conditions of impaired glucose metabolism vs normal controls.
In addition to its use in characterizing glucose transport in striated muscle by GLUT4 and GLUT1, our model could be extended to evaluate renal (or intestinal) handling of glucose, which is transported into the cells by sodium-glucose cotransporters (SGLTs). Glucose transport in the kidney is a two-step process with SGLTs facilitating the first step at the luminal surface of proximal tubular cells and GLUT2 facilitating the second at the basolateral surface. For this, our model would be modified to include an additional transport step. This would be particularly promising with 6FDG because it is well-transported by both GLUTs and SGLTs.7
CONCLUSIONS
We have proposed and mathematically demonstrated local identifiability properties of a new model for describing transport and phosphorylation of glucose and its analogs in skeletal muscle. Except for intracellular glucose concentration, parameter estimates generally appear to be very accurate (unbiased) under various conditions. Unlike other PET models, our model has fewer model parameters to be estimated and obviates the use of lumped constant. Another unique feature of our model is that it provides direct estimates of interstitial and intracellular glucose concentrations (ISg and ICg, respectively, in the model). Moreover, we simulate the effect of insulin action by increasing maximal velocities for glucose transport and phosphorylation (i.e., VG and VH). In our model, this causes increases in cellular influx and efflux of glucose and glucose phosphorylation rate. These changes are consistent with the known physiological response to insulin stimulation. With these results, we expect that conditions associated with impaired glucose transport and abnormal glucose metabolism can be detected and evaluated by our model.
Table 5.
Summary of parameter estimates using different Michaelis constants for basal conditions.
| 500 sets of parameter estimates (mean ± SD) | ||||||
|---|---|---|---|---|---|---|
| Basal conditions | True | Assumed | k1 (mL/mL min−1) | ISg (mM) | ICg (mM) | fIS |
| True Michaelis constants | 0.040 ± 0.001 | 5.12 ± 0.04 | 0.13 ± 0.16 | 0.25 ± 0.00 | ||
| 3.5 | 2.8 | 0.040 ± 0.001 | 4.94 ± 0.06 | 0.15 ± 0.17 | 0.25 ± 0.00 | |
| 3.5 | 4.5 | 0.040 ± 0.001 | 5.25 ± 0.03 | 0.12 ± 0.16 | 0.25 ± 0.00 | |
| 0.13 | 0.104 | 0.040 ± 0.001 | 5.11 ± 0.04 | 0.12 ± 0.15 | 0.25 ± 0.00 | |
| 0.13 | 0.156 | 0.040 ± 0.001 | 5.12 ± 0.04 | 0.12 ± 0.16 | 0.25 ± 0.02 | |
| 10 | 8 | 0.040 ± 0.001 | 5.11 ± 0.03 | 0.01 ± 0.02 | 0.24 ± 0.00 | |
| 10 | 12 | 0.040 ± 0.001 | 5.15 ± 0.04 | 0.36 ± 0.16 | 0.25 ± 0.00 | |
| 8 | 6.4 | 0.040 ± 0.001 | 5.29 ± 0.03 | 0.37 ± 0.15 | 0.25 ± 0.00 | |
| 8 | 9.6 | 0.040 ± 0.001 | 4.96 ± 0.03 | 0.02 ± 0.04 | 0.24 ± 0.00 | |
| 0.17 | 0.136 | 0.040 ± 0.001 | 5.12 ± 0.05 | 0.12 ± 0.15 | 0.25 ± 0.00 | |
| 0.17 | 0.204 | 0.040 ± 0.001 | 5.12 ± 0.04 | 0.12 ± 0.15 | 0.25 ± 0.00 | |
Table 6.
Summary of parameter estimates using different Michaelis constants for EH conditions.
| 500 sets of parameter estimates (mean ± SD) | ||||||
|---|---|---|---|---|---|---|
| EH conditions | True | Assumed | k1 (mL/mL min−1) | ISg (mM) | ICg (mM) | fIS |
| True Michaelis constants | 0.045 ± 0.002 | 3.04 ± 0.13 | 0.19 ± 0.15 | 0.24 ± 0.02 | ||
| 3.5 | 2.8 | 0.045 ± 0.002 | 2.77 ± 0.14 | 0.27 ± 0.14 | 0.24 ± 0.01 | |
| 3.5 | 4.5 | 0.044 ± 0.002 | 3.27 ± 0.10 | 0.10 ± 0.12 | 0.25 ± 0.01 | |
| 0.13 | 0.104 | 0.045 ± 0.002 | 3.01 ± 0.11 | 0.16 ± 0.14 | 0.24 ± 0.02 | |
| 0.13 | 0.156 | 0.045 ± 0.002 | 3.07 ± 0.15 | 0.21 ± 0.17 | 0.25 ± 0.02 | |
| 10 | 8 | 0.046 ± 0.002 | 3.01 ± 0.08 | 0.01 ± 0.03 | 0.23 ± 0.01 | |
| 10 | 12 | 0.043 ± 0.002 | 3.06 ± 0.11 | 0.36 ± 0.13 | 0.26 ± 0.01 | |
| 8 | 6.4 | 0.043 ± 0.002 | 3.33 ± 0.08 | 0.41 ± 0.09 | 0.26 ± 0.01 | |
| 8 | 9.6 | 0.047 ± 0.002 | 2.77 ± 0.07 | 0.01 ± 0.03 | 0.23 ± 0.01 | |
| 0.17 | 0.136 | 0.045 ± 0.002 | 3.08 ± 0.16 | 0.22 ± 0.18 | 0.25 ± 0.02 | |
| 0.17 | 0.204 | 0.044 ± 0.002 | 3.01 ± 0.12 | 0.16 ± 0.14 | 0.25 ± 0.02 | |
ACKNOWLEDGMENTS
This work was supported by National Institute of Diabetes and Digestive and Kidney Diseases Grant No.: R01 DK082423 (PIs: Muzic and Ismail-Beigi). The authors thank Dr. Chandramouli for discussion on our proposed method.
Appendix A: Identifiability Analysis
To analyze a priori identifiability of the final model parameters using the transfer function method,40 we start with the model equations shown in Eqs. 7–9.
| (A1) |
| (A2) |
| (A3) |
In addition, the model output can be written as:
| (A4) |
By taking Laplace transform of Eqs. A1–A3, one has
| (A5) |
| (A6) |
| (A7) |
Solving for IS'a(s), IC'a(s) and IS'a(s) one has
| (A8) |
| (A9) |
| (A10) |
Thus, the Laplace transform of CPET(t) can be written as
| (A11) |
As a result, the six known observational parameters are
| (A12) |
| (A13) |
| (A14) |
| (A15) |
| (A16) |
| (A17) |
Thus, these six observational parameters are a priori uniquely identifiable. To assess the identifiability of the model parameters k1, k2, k3a, k4a, k5a and fb, we solve for them in terms of the observational parameters
| (A18) |
| (A19) |
| (A20) |
| (A21) |
| (A22) |
| (A23) |
The unique solutions indicate these six parameters are a priori uniquely identifiable. To test whether fIS, fIC, ISg and ICg are a priori uniquely identifiable, we solve for these in terms of the observational parameters. For fIS, we substitute k2=k1/fIS, into Eq. A19 to obtain
| (A24) |
indicating it is a priori uniquely identifiable. The analyses for k1, fIS, fIC, ISg, and ICg are more complex. As we described in Sec. B, given known Michaelis constants and Pg, the rate constants k3a, k4a and k5a can expressed in terms of k1, fIS, fIC, ISg, and ICg,
| (A25) |
| (A26) |
| (A27) |
Substituting Eqs. A25–A27 into Eqs. A20–A22, we can solve for fIC, ISg and ICg in terms of known parameters, Pg, , , , , Φ1, Φ2, Φ3, Φ4 and Φ5.
| (A28) |
| (A29) |
| (A30) |
According to Eq. A28, since b2−4ac≥0, ISg may have two real solutions. This shows the model, in terms of our final parameterization, can have at most two solutions. Accordingly, all six model parameters, k1, fIS, fIC, fb, ISg and ICg are a priori locally identifiable.
The identifiability of the proposed model derived above is for a phosphorylated glucose analog (i.e., 2FDG). For a non-phosphorylated glucose analog (i.e., 6FDG), we still have six model parameters, k1 fIS, fIC, fb, ISg and ICg. The Laplace transform of CPET(t) can be simply obtained by setting the rate constant k5a of Eq. A11 to zero. As a result, there are five known observational parameters and six unknown model parameters, indicating that these six model parameters are non-identifiable. However, since we assume for skeletal muscle fb + fIS + fIC=l (i.e., fIC=l −fIS − fb), the number of unknown model parameters is reduced from six to five. Again, we can solve for ISg and ICg in terms of known parameters, Pg, , and five observational parameters. Analogously, ISg may have two real solutions. Accordingly, all five model parameters, k1, fIS, fb, ISg and ICg are a priori locally identifiable.
In the case of a two-injection study, as we propose, which uses 6FDG followed by 2FDG, the information content of the combined data set is at least as great as that obtained with either 2FDG or 6FDG used alone. Consequently, the two-injection study is a priori locally identifiable.40
Appendix B: Analysis of Noise levels
In the figure shown below, we compare the tissue time-activity curves (TACs) for rat skeletal muscle during [18F]6FDG PET scans obtained from a preliminary study to those from the simulation. We observe that the noise level (α=0.05) used in simulation is in the range of that obtained from animal studies. To quantitatively estimate the noise level (a), we fit the noisy TAC ((, shown below) using the 5K model and treat the model fit as noise-free data (Di). Then, the noise level would be estimated by calculating the standard deviation of . As a result, the estimated noise level is 0.03 which shows that the value of α = 0.05 might be a bit pessimistic indicating we have taken a conservative approach of testing conditions that may be a little more challenging than reality.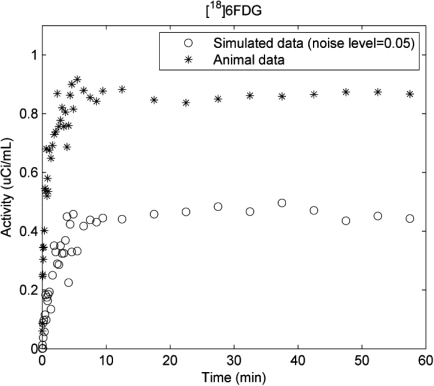
Appendix C: Additional Simulation Results
References
- Sokoloff L., Reivich M., Kennedy C., Des Rosiers M. H., Patlak C. S., Pettigrew K. D., Sakurada O.,and Shinohara M., “The [14C]deoxyglucose method for the measurement of local cerebral glucose utilization: theory, procedure, and normal values in the conscious and anesthetized albino rat,” J. Neurochem. 28, 897–916 (1977). 10.1111/j.1471-4159.1977.tb10649.x [DOI] [PubMed] [Google Scholar]
- Phelps M. E., Huang S. C., Hoffman E. J., Selin C., Sokoloff L., and Kuhl D. E., “Tomographic measurement of local cerebral glucose metabolic rate in humans with (F-18)2-fluoro-2-deoxy- D-glucose: Validation of method,” Ann. Neurol. 6, 371–388 (1979). 10.1002/ana.v6:5 [DOI] [PubMed] [Google Scholar]
- Bertoldo A., Peltoniemi P., Oikonen V., Knuuti J., Nuutila P., and Cobelli C., “Kinetic modeling of [(18)F]FDG in skeletal muscle by PET: A four-compartment five-rate-constant model,” Am. J. Physiol. Endocrinol. Metab. 281, 524–536 (2001).http://ajpendo.physiology.org/content/281/3/E524.full [DOI] [PubMed] [Google Scholar]
- Bertoldo A., Pencek R. R., Azuma K., Price J. C., Kelley C., Cobelli C., and Kelley D. E., “Interactions between delivery, transport, and phosphorylation of glucose in governing uptake into human skeletal muscle,” Diabetes 55, 3028–3037 (2006). 10.2337/db06-0762 [DOI] [PubMed] [Google Scholar]
- Schuier F., Orzi F., Suda S., Lucignani G., Kennedy C., and Sokoloff L., “Influence of plasma glucose concentration on lumped constant of the deoxyglucose method: Effects of hyperglycemia in the rat,” J. Cereb. Blood. Flow. Metab. 10, 765–773 (1990). 10.1038/jcbfm.1990.134 [DOI] [PubMed] [Google Scholar]
- Suda S., Shinohara M., Miyaoka M., Lucignani G., Kennedy C., and Sokoloff L., “The lumped constant of the deoxyglucose method in hypoglycemia: Effects of moderate hypoglycemia on local cerebral glucose utilization in the rat,” J. Cereb. Blood. Flow. Metab. 10, 499–509 (1990). 10.1038/jcbfm.1990.92 [DOI] [PubMed] [Google Scholar]
- Landau B. R., C. L.Spring-Robinson, Jr. Muzic R. F., Rachdaoui N., Rubin D., Berridge M. S., Schumann W. C., Chandramouli V., Kern T. S., and Ismail-Beigi F., “6-Fluoro-6-deoxy-D-glucose as a tracer of glucose transport,” Am. J. Physiol. Endocrinol. Metab. 293, 237–245 (2007). 10.1152/ajpendo.00022.2007 [DOI] [PubMed] [Google Scholar]
- Johnson J. A. and Wilson T. A., “A model for capillary exchange,” Am. J. Physiol. 210, 1299–1303 (1966).http://ajplegacy.physiology.org/content/210/6/1299.long [DOI] [PubMed] [Google Scholar]
- Renkin E. M., “Transport of potassium-42 from blood to tissue in isolated mammalian skeletal muscle,” Am. J. Physiol. 197, 1205–1210 (1959).http://ajplegacy.physiology.org/content/197/6/1205.abstract [DOI] [PubMed] [Google Scholar]
- Dixon M. and Webb E. C., Enzymes (Academic, Inc., New York, 1979). [Google Scholar]
- Taylor L. P. and Holman G. D., “Symmetrical kinetic parameters for 3-O-methyld-glucose transport in adipocytes in the presence and absence of insulin,” Biochim. Biophys. Acta. 642, 325–335 (1981). 10.1016/0005-2736(81)90449-1 [DOI] [PubMed] [Google Scholar]
- Crane P. D., Pardridge W. M., Braun L. D., and Oldendorf W. H., “Kinetics of transport and phosphorylation of 2-fluoro-2-deoxy-D-glucose in rat brain,” J. Neurochem. 40, 160–167 (1983). 10.1111/j.1471-4159.1983.tb12666.x [DOI] [PubMed] [Google Scholar]
- Mori K. and Maeda M., “Use of [3H]methylglucose and [14C]iodoantipyrine to determine kinetic parameters of glucose transport in rat brain,” Am. J. Physiol. 272, 163–171 (1997).http://ajpregu.physiology.org/content/272/1/R163.abstract [DOI] [PubMed] [Google Scholar]
- Pardridge W. M. and Oldendorf W. H., “Kinetics of blood-brain transport of hexoses,” Biochim. Biophys. Acta. 382, 377–392 (1975). 10.1016/0005-2736(75)90279-5 [DOI] [PubMed] [Google Scholar]
- Cieslar J., Huang M. T., and Dobson G. P., “Tissue spaces in rat heart, liver, and skeletal muscle in vivo,” Am. J. Physiol. 275, 1530–1536 (1998).http://ajpregu.physiology.org/content/275/5/R1530.full [DOI] [PubMed] [Google Scholar]
- Cobelli C., Foster D., and Toffolo G., Tracer Kinetics in Biomedical Research: From Data to Model (Kluwer Academic/ Plenum, New York, 2001). [Google Scholar]
- R. F.Muzic, Jr. and Cornelius S., “COMKAT: Compartment model kinetic analysis tool,” J. Nucl. Med. 42, 636–645 (2001).http://jnm.snmjournals.org/content/42/4/636.full [PubMed] [Google Scholar]
- Fang Y. H., Asthana P., Salinas C., Huang H. M., and R. F.MuzicJr., “Integrated software environment based on COMKAT for analyzing tracer pharmacokinetics with molecular imaging,” J. Nucl. Med. 51, 77–84 (2010). 10.2967/jnumed.109.064824 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fang Y. H. and R. F.Muzic, Jr. “Spillover and partial-volume correction for image-derived input functions for small-animal 18F-FDG PET studies,” J. Nucl. Med. 49, 606–614 (2008). 10.2967/jnumed.107.047613 [DOI] [PubMed] [Google Scholar]
- Halseth A. E., Bracy D. P., and Wasserman D. H., “Functional limitations to glucose uptake in muscles comprised of different fiber types,” Am. J. Physiol. Endocrinol. Metab. 280, 994–999 (2001).http://ajpendo.physiology.org/content/280/6/E994.long [DOI] [PubMed] [Google Scholar]
- Muzi M., Freeman S. D., Burrows R. C., Wiseman R. W., Link J. M., Krohn K. A., Graham M. M., and Spence A. M., “Kinetic characterization of hexokinase isoenzymes from glioma cells: implications for FDG imaging of human brain tumors,” Nucl. Med. Biol. 28, 107–116 (2001). 10.1016/S0969-8051(00)00201-8 [DOI] [PubMed] [Google Scholar]
- Spring-Robinson C. L., Chandramouli V., Schumann W. C., Faulhaber P. F., Wang Y., Wu C., Ismail-Beigi F., and R. F.MuzicJr., “Uptake of 18F-labeled 6-fluoro-6-deoxy-D-glucose by skeletal muscle is responsive to insulin stimulation,” J. Nucl. Med. 50, 912–919 (2009). 10.2967/jnumed.109.062687 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steven W. C., Karen S. H., Brad J. B., Poole D. C., and Musch T. I., “Effects of Type II diabetes on exercising skeletal muscle blood flow in the rat,” J. Appl. Physiol. 109, 1347–1353 (2010). 10.1152/japplphysiol.00668.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- King P. A., Hirshman M. F., Horton E. D, and Horton E. S., “Glucose transport in skeletal muscle membrane vesicles from control and exercised rats,” Am. J. Physiol. 257, C1128–C1134 (1989).http://ajpcell.physiology.org/content/257/6/C1128.reprint [DOI] [PubMed] [Google Scholar]
- Postic C., Leturque A., Rencurel F., Printz R. L., Forest C., Granner D. K., and Girard J., “The effects of hyperinsulinemia and hyperglycemia on GLUT4 and hexokinase II mRNA and protein in rat skeletal muscle and adipose tissue,” Diabetes 42, 922–929 (1993). 10.2337/diabetes.42.6.922 [DOI] [PubMed] [Google Scholar]
- Vincent M. A., Dawson D., Clark A. D., Lindner J. R., Rattigan S., Clark M. G., and Barrett E. J., “Skeletal muscle microvascular recruitment by physiological hyperinsulinemia precedes increases in total blood flow,” Diabetes 51, 42–48 (2002). 10.2337/diabetes.51.1.42 [DOI] [PubMed] [Google Scholar]
- Gudbjörnsdóttir S., Sjöstrand M., Strindberg L., Wahren J., and Lönnroth P., “Direct measurements of the permeability surface area for insulin and glucose in human skeletal muscle,” J. Clin. Endocrinol. Metab. 88, 4559–4564 (2003). 10.1210/jc.2003-030434 [DOI] [PubMed] [Google Scholar]
- R. F.MuzicJr. and Christian B. T., “Evaluation of objective functions for estimation of kinetic parameters,” Med. Phys. 33, 342–353 (2006). 10.1118/1.2135907 [DOI] [PubMed] [Google Scholar]
- Coleman T. F. and Li Y., “An interior trust region approach for nonlinear minimization subject to bounds,” SIAM. J. Optim. 6, 418–445 (1996). 10.1137/0806023 [DOI] [Google Scholar]
- Huang S. C., Phelps M. E., Hoffman E. J., Sideris K., Selin C. J., and Kuhl D. E., “Noninvasive determination of local cerebral metabolic rate of glucose in man,” Am. J. Physiol. 238, 69–82 (1980). [DOI] [PubMed] [Google Scholar]
- Morgan H. E., Neely J. R., and Kira Y., “Factors determining the utilization of glucose in isolated rat hearts,” Basic. Res. Cardiol. 79, 292–299 (1984). 10.1007/BF01908029 [DOI] [PubMed] [Google Scholar]
- Behrooz A. and Ismail-Beigi F., “Stimulation of Glucose Transport by Hypoxia: Signals and Mechanisms,” News. Physiol. Sci. 14, 105–110 (1999). [DOI] [PubMed] [Google Scholar]
- Ferrannini E., Smith J. D., Cobelli C., Toffolo G., Pilo A., and DeFronzo R. A., “Effect of insulin on the distribution and disposition of glucose in man,” J. Clin. Invest. 76, 357–364 (1985). 10.1172/JCI111969 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park C. R., Reinwein D., Henderson M. J., Cadenas E., and Morgan H. E., “The action of insulin on the transport of glucose through the cell membrane,” Am. J. Med. 26, 674–684 (1959). 10.1016/0002-9343(59)90227-X [DOI] [PubMed] [Google Scholar]
- Bonadonna R. C., Del Prato S., Saccomani M. P., Bonora E., Gulli G., Ferrannini E., Bier D., Cobelli C., and DeFronzo R. A., “Transmembrane glucose transport in skeletal muscle of patients with non-insulin- dependent diabetes,” J. Clin. Invest. 92, 486–494 (1993). 10.1172/JCI116592 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonadonna R. C., Saccomani M. P., and Cobelli C., “In vivo glucose transport in human skeletal muscle: tools, problems and perspectives,” Baillieres Clin. Endocrinol. Metab. 7, 929–960 (1993). 10.1016/S0950-351X(05)80240-X [DOI] [PubMed] [Google Scholar]
- Ng J. M., Kelley D. E., and Goodpaster B. H., “Mechanisms of insulin resistance assessed by dynamic in-vivo positron emission tomography imaging,” Curr. Opin. Clin. Nutr. Metab. Care 12, 508–512 (2009). 10.1097/MCO.0b013e32832eb59a [DOI] [PubMed] [Google Scholar]
- Williams K. V., Price J. C., and Kelley D. E. “Interactions of impaired glucose transport and phosphorylation in skeletal muscle insulin resistance: A dose-response assessment using positron emission tomography,” Diabetes 50, 2069–2079 (2001). 10.2337/diabetes.50.9.2069 [DOI] [PubMed] [Google Scholar]
- Pendergrass M., Bertoldo A., Bonadonna R., Nucci G., Mandarino L., Cobelli C., and Defronzo R. A., “Muscle glucose transport and phosphorylation in type 2 diabetic, obese nondiabetic, and genetically predisposed individuals,” Am. J. Physiol. Endocrinol. Metab. 292, 92–100 (2007). 10.1152/ajpendo.00617.2005 [DOI] [PubMed] [Google Scholar]
- Cobelli C., Foster D., and Toffolo G.. Tracer Kinetics in Biomedical Research: From Data to Model. New York: Kluwer Academic/Plenum, 2001. [Google Scholar]