Role of stochastic processes in maintaining discrete strain structure in antigenically diverse pathogen populations

Abstract

Many highly diverse pathogen populations appear to exist stably as discrete antigenic types despite evidence of genetic exchange. It has been shown that this may arise as a consequence of immune selection on pathogen populations, causing them to segregate permanently into discrete nonoverlapping subsets of antigenic variants to minimize competition for available hosts. However, discrete antigenic strain structure tends to break down under conditions where there are unequal numbers of allelic variants at each locus. Here, we show that the inclusion of stochastic processes can lead to the stable recovery of discrete strain structure through loss of certain alleles. This explains how pathogen populations may continue to behave as independently transmitted strains despite inevitable asymmetries in allelic diversity of major antigens. We present evidence for this type of structuring across global meningococcal isolates in three diverse antigens that are currently being developed as vaccine components.

Many pathogen species, including those causing AIDS, malaria, and influenza, exhibit high levels of diversity among genes encoding antigenic proteins, enabling immune escape at both the individual and population levels. Many of the relevant antigens also have important functional roles in the life history of the pathogen, however. The potential antigenic diversity of pathogen populations can thus be represented by either a continuous or discrete “strain space” whose form and boundaries derive from their biological roles as well as considerations of molecular structure. The behavior of the pathogen population within this antigenic strain space is determined by the degree to which infection of a host with one antigenic type or strain generates cross-protective immune responses against other strains. This cross-protection may be (i) strain-transcending, where infection with one strain provides an equal level of protection against all other strains (1, 2); (ii) strain-specific, where strains have well-defined antigenic relationships with each other (3–7); or (iii) a combination of both (8, 9). In cases ii and iii, competition for hosts when immunological cross-protection is strong can cause the pathogen population to become polarized in strain space. In models in which immunity is directed against a specific number of antigenic loci, each with a finite number of allelic variants, this can manifest as the stable coexistence of a subset of discrete discordant strains with nonoverlapping antigenic variant repertoires (6, 7).

The emergence of strains with completely nonoverlapping combinations of antigenic alleles within these systems is a consequence of the inbuilt symmetry imposed by assuming equal levels of allelic diversity among loci, however. Theoretical studies have shown that the signature of immune selection can become considerably more complex in the absence of this symmetry (10, 11), such that dominant strains within pathogen populations may show substantial allelic overlap. It is therefore surprising that evidence of discrete strain structure has been found in several pathogen species. For example, the pathogenic bacterial species Neisseria meningitidis exhibits a clear nonoverlapping structure among hypervariable regions of immunodominant subcapsular antigens at the population level (7, 12, 13). Populations of the relapsing fever spirochete Borrelia hermsii are also characterized by discrete independent strains in which repertoires of immunodominant outer membrane proteins in wild isolates are either identical or completely distinct from each other (14). The long-term population structure of two outer membrane proteins of global Group A Streptococcus exhibit distinct combinations of alleles with minimal overlap between strains (14, 15). Similarly, recent analysis of the tick-borne bacteria Anaplasma marginale, a prevalent livestock pathogen, has shown that the coinfection of cattle with different strains relies on the expression of nonoverlapping variants of the major antigen family by superinfecting strains (16). For the human malaria parasite, Plasmodium falciparum, analysis of serological responses to disease-causing isolates in children indicates that parasites are behaving phenotypically as independent strains, despite the variety of diverse antigenic determinants expressed during infection (17–21). Although the specific epitopes involved in these responses have not yet been elucidated, wild parasite isolates in areas of intense transmission do not appear to share genetic sequences among the var gene family encoding the immunodominant variant surface antigen P. falciparum Erythrocyte Membrane Protein 1 (22). Recent analysis of a malaria parasite protein and vaccine candidate, Merozoite Surface Protein-3, has also shown this type of discrete pattern among its relevant epitope regions (23).

Given that immunodominant antigens are likely to contain epitopes with varying levels of diversity, imposed by their structural position and molecular role within the protein (24), the conformation of real pathogen populations to theoretical predictions based on assumptions of allelic symmetry is difficult to explain. Here, we show that stochasticities, inherent to dynamic processes of infection and immunity but often ignored in mathematical frameworks, can explain this paradox. We explore the effects of immune selection on a pathogen population defined by antigenic loci with varying degrees of functional constraints, as reflected by asymmetries in allelic diversity, using a stochastic model that explicitly includes recombination and mutation, and permits extinction of alleles. We show that these processes qualitatively change the resulting pathogen population structure and allow for the emergence of simple discrete strain structure over a wide range and variability of functional constraints on the relevant antigens. We examine a global database of meningococcal isolates and find that regional diversities are similar at three different antigenic loci, despite substantial differences in their diversities. Our results provide an important example in which a stochastic individual-based model is more successful in reconciling pattern with process than its deterministic counterpart (25).

Results

We developed stochastic analogs of multilocus models (6) in which pathogens were defined by two or three antigenic loci, with each locus having the same (symmetric) or different (asymmetric) number of possible alleles. To compare the deterministic and stochastic model outcomes, we used two metrics of population structure: diversity, D, and discordance, f*, measuring the distribution of strain prevalence and the level of relatedness (i.e., overlap in variant repertoires) in the circulating strains, respectively (more details are presented in Methods). For symmetric systems, the general dynamics of both deterministic and stochastic models are equivalent to those described by Gupta et al. (7), and there is a clear relationship between the diversity and discordance of the pathogen population and the strength of immunological cross-protection (γ, the original model dynamics are illustrated in Fig. S1). When γ is low, all pathogen strains can be found at equal prevalence, resulting in maximum diversity (D = 1). Because strains with overlapping antigenic determinants coexist, the degree of nonoverlapping structure or discordance (f*) is also very low. When γ is high, diversity drops and the degree of discordance rises as a subset of nonoverlapping strains emerges (Fig. S2).

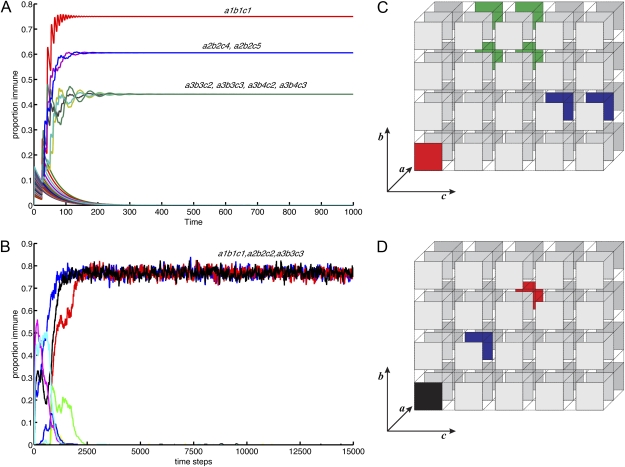
Asymmetries in the number of alleles at each locus introduce important differences between the deterministic and stochastic models, however; Fig. 1 A and B show simulations for the deterministic and stochastic models, respectively, of a multilocus system under strong immune selection with three, four, and five alleles at each of three loci. For the deterministic model (Fig. 1A), the asymmetric case results in a highly structured equilibrium in which dominant and subdominant sets of strains are maintained and strains with entirely nonoverlapping combinations of alleles cannot exclude all others because of the geometry of the system. Here, alleles at the least diverse locus are associated with more than one allele at the more diverse loci because these have an equal competitive advantage. Fig. 1C illustrates the dimensions of this strain space at equilibrium. The stochastic model simulation (Fig. 1B) diverges significantly from its deterministic counterpart: Only 3 of the possible 60 strains continue to coexist. In other words, under high levels of immune selection, most of the alleles initially present (or generated by means of mutation) at the more diverse loci are driven to extinction. Fig. 1D illustrates the corresponding dimensions of strain space for the stochastic simulation, showing the contrast between the highly structured patterns of dominant and subdominant strains in the deterministic system and the simple nonoverlapping structures in the stochastic system.

Fig. 1.

Examples of time series for deterministic (A) and stochastic (B) 3 × 4 × 5 allele models showing the proportion of the population immune to particular strains. Each strain is labeled according to the locus (a, b, and c), with a subscript representing the allele (between 1 and 5). Parameter values for the deterministic model: β = 4, σ = 1, μ = 0.02. (C) Dimensions of strain space at equilibrium for the deterministic model corresponding to A. (D) Dimensions of strain space at equilibrium for the stochastic model corresponding to B. In both, the three-allele locus is represented as layers one behind the other and the strains are colored according to the allele expressed at this locus (e.g., the green squares in C all share allele 3 at locus a).

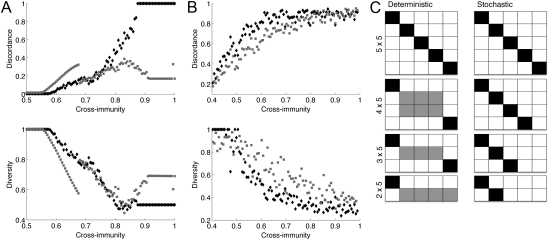
The impact of these contrasting dynamics on the discordance and diversity of the pathogen populations within the model systems is shown in Fig. 2. For the deterministic model, the asymmetric case results in a number of complex and variably structured populations in which dominant and subdominant sets of strains are maintained at equilibrium as cross-immunity (γ) increases. As a result, higher levels of diversity can be maintained even when γ is high. Fig. 2A illustrates this result, showing the difference in the diversity and discordance profiles of the symmetric and asymmetric deterministic systems for the two-locus case, where (i) each locus has five alleles (in black) and (ii) one locus has two alleles and one locus has five alleles (in gray). Fig. 2B shows the same metrics for the stochastic version. It is clear from these figures that the stochastic model diverges significantly from its deterministic counterpart as immune selection (γ) increases. Although the 2 × 5 system maintains slightly more diversity and shows more overlap among strains than the symmetric system at intermediate levels of immune selection, when immune selection is strong, only 2 of the possible 10 strains continue to coexist. Thus, both the symmetric and asymmetric systems show the same high degree of discordance and low levels of diversity under very strong immune selection, because the 2 × 5 system effectively collapses to a symmetric 2 × 2 system. This reversion to symmetry facilitates the dominance of completely nonoverlapping subsets of strains and is stable even in the presence of extremely high rates of recombination and mutation. Fig. 2C illustrates the structure of strain space for different deterministic and stochastic systems at equilibrium when cross-immunity is strong (and see Figs. S3 and S4).

Fig. 2.

Comparison of the relationship between diversity/discordance and cross-immunity for the symmetric 5 × 5 system (black diamonds) and an asymmetric 2 × 5 system (gray squares) for the deterministic (A) and stochastic (B) models. Each point in the stochastic figures represents the mean of simulations for which cross-immunity fell within a bin of 0.02. Parameter values for the deterministic model: β = 4, σ = 1, μ = 0.02. (C) Patterns of dominance observed at high levels of cross-immunity for equivalent deterministic and stochastic two-locus systems. Alleles of locus 1 are represented by rows, and alleles of locus 2 are represented by columns, such that each square in the matrix represents one allelic combination. Black squares represent dominance at equilibrium of particular combinations, and white squares represent the absence of particular combinations. Gray squares represent subdominant (in terms of prevalence) allelic combinations.

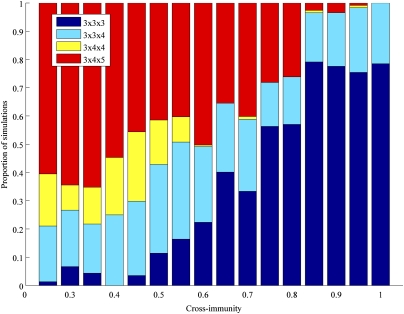
The extinction of alleles occurring in the stochastic system allows the pathogen population to reduce competition among strains, albeit at the expense of diversity. Fig. 3 shows the distribution of equilibrium outcomes for increasing levels of immune selection within the stochastic framework. As cross-immunity increases, pathogen populations become increasingly dominated by strains with entirely nonoverlapping antigen repertoires. The dimensions of strain space among these populations were therefore determined by the number of distinct allelic forms possible at the most constrained locus (in this case, the locus with 3 allelic variants), and the emergence of diversity among the less constrained loci becomes unfeasible with increasing competition. An exploration of the effects of host contact network structure was performed to determine how local mixing might affect the structure of these pathogen populations. Consistent with our previous work (26), although a host population characterized only by local mixing produces less structured pathogen populations, only a few long-range connections (coupled with strong cross-immunity) are sufficient to structure the entire pathogen population into symmetric nonoverlapping combinations of alleles (Fig. S5). Importantly, the stochastic model is necessarily constrained in its population size. We have shown that increasing the population size does not change the outcome at equilibrium (Fig. S6), but we do expect that the speed at which equilibrium is reached will be increased in small populations.

Fig. 3.

Relationship between the dimensions of strain space and cross-immunity for the three-locus 3 × 4 × 5 stochastic model. Stacked bars represent the proportion of simulations with particular dimensions at equilibrium.

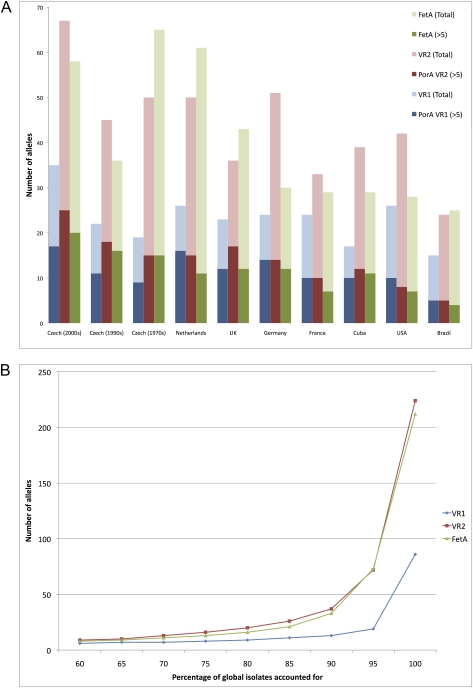
To determine whether the structuring observed in our model output was evident in real pathogen populations, we interrogated a global database of meningococcal isolates (www.pubmlst.org). We compiled a list of allelic variants at two meningococcal outer membrane antigens that exhibit considerable diversity and have been included in strain-specific vaccines because of their immunogenicity (27, 28). For each region, we examined the hypervariable regions (VR1 and VR2) of the PorA locus, which may be considered as separate epitopes because they recombine freely (12), and the diverse FetA locus. We have previously shown nonoverlapping structure among these antigens in one region and explored the dynamics of these antigens over time with respect to housekeeping loci (12). Here, we focus on the antigenic determinants on a global scale. Fig. 4A illustrates the difference between the number of allelic variants at each locus found in more than five isolates compared with the total number of allelic variants found in each region. Although the difference in the total diversities in each locus is substantial when considering the very rare alleles, they show similar numbers of alleles when considering strains appearing at significant frequencies in the population (here, we chose an arbitrary threshold of 5, but the outcome was insensitive to the exact number). We can explain this pattern within the framework of our model by assuming strain space is continually being explored at the more diverse PorA VR2 and FetA loci, generating many single variants, but the dominant strains in the population are constrained by the level of diversity at the PorA VR1 locus. Table 1 shows the number of isolates analyzed and the f* values calculated for the prevalent variants for each country, indicating the extent of nonoverlapping structure among the dominant strains. The distribution of allele frequencies observed in these regions is similar to the larger simulations of our model (SI Text), and particularly surprising is the number of f* values close to or equal to 1, given that we would expect very low values from the deterministic model with many alleles even under relatively strong immune selection (Figs. S7 and S8). Interestingly, when we pooled all the isolates in the database, although the diversity of both FetA and PorA VR2 was extremely high when considering every possible allele, the number of alleles at all three loci was approximately the same for nearly 70% of all global isolates (Fig. 4B). For PorA VR1, the number of alleles was more or less constant for up to 90% of all isolates. We believe this pattern is consistent with our hypothesis that the diversity of PorA VR1 may be constraining the diversities of PorA VR2 and FetA.

Fig. 4.

(A) Regional diversities of meningococcal antigens PorA VR1 and VR2 and FetA. Each bar represents the total number of alleles observed in each region (lighter shades) and the subset of alleles represented by more than five isolates (darker shades). (B) Cumulative number of alleles found in all global isolates in the database.

Table 1.

f* values calculated for the dominant strains (those shown in the darker shades in Fig. 4B) from each country, with sample sizes (n) also shown

	Sample size (n)	f* PorA VR1/VR2	f* PorA VR1/FetA	f* PorA VR2/FetA
United Kingdom	335	0.690	0.253	0.30
France	126	1	0.519	1
Germany	265	0.688	0.376	0.498
The Netherlands	277	0.782	1	1
Brazil	77	0.809	1	0.712
United States	117	0.797	1	1
Cuba	408	0.957	0.712	0.951
Czech Republic in 2000s	657	0.548	0.274	0.272
Czech Republic in 1990s	297	0.721	0.662	0.911
Czech Republic in 1970s	286	0.939	0.475	0.541
Mean	285	0.793	0.627	0.719

Discussion

Understanding the evolutionary forces shaping the structure of pathogen populations is an important goal of mathematical models. Although deterministic models provide important insights into these mechanisms, stochastic processes, such as extinction, can play a crucial role in the real world. Deterministic frameworks (10, 11) have indicated that asymmetries in the allelic diversities of different immunodominant antigens, attributable to such factors as varying functional constraints, can lead to a higher degree of antigenic overlap among prevailing strains within pathogen populations than expected when loci are equally diverse. Even when immune selection is strong, these allelic asymmetries can prevent the emergence of entirely nonoverlapping strains in the deterministic model. However, a stochastic version of the model illustrates how the extinction of alleles at more diverse loci can lead to the recovery of a symmetric strain space characterized by entirely nonoverlapping strains. Many important pathogens have multiple immunodominant antigenic determinants, and it is extremely likely that some will be more functionally or otherwise restricted in their diversities. The results presented here may provide the answer to how so many such pathogen populations continue to behave as independently transmitted strains despite these inevitable asymmetries. We propose that the stochastic processes delineated here can explain the success of simple symmetric and deterministic models in describing the population structure of pathogens with multiple immunodominant loci ranging from N. meningitidis to P. falciparum and A. marginale.

There have been various theoretical studies on the effect of host immunity on the population structures of antigenically diverse pathogens. The study presented here concentrates on systems in which the relationship between any two pathogenic variants or strains is clearly defined by an overlap in their respective antigenic repertoire at loci under immune selection. As such, two strains will interfere with each other's transmission through the action of cross-immunity if they have one or more alleles in common, and the actual degree of overlap (in terms of common/shared alleles) does not alter the degree of interference. It will be interesting to see how our results apply to systems where the degree of antigenic overlap also determines the degree of cross-immunity (11, 29); we may hypothesize, however, that these systems will also tend toward complete discordance when stochastic extinction occurs.

Our results indicate that the extinction of alleles at more diverse antigenic loci will occur more rapidly in small or spatially structured host populations. The effect of population size on pathogen diversity has previously been demonstrated, for example, by Abu-Raddad and Ferguson (1), although the system considered in their study allowed for unconstrained genetic/antigenic evolution and the results crucially depended on relative pathogen fitness and the rate at which strains are introduced and replaced within the population. In contrast, our results do not depend on those parameters and are robust to changes in the shape and dimension of strain-space.

The data presented here provide evidence for the signature of these processes occurring within a range of globally distributed populations of N. meningitidis. Our model framework can explain how the enormous diversity of certain meningococcal antigens may be constrained by the levels of diversity present at another antigenic locus. Note that we have previously shown that the nonoverlapping structure at these antigenic loci is not found among housekeeping genes in the same isolates (12), highlighting the fact that recombination can allow for divergent evolutionary trajectories among genes within the same isolates.

Our framework also has important ramifications for invasion of endemic populations by new strains, because pathogens must acquire different epitopes or alleles at every immunodominant locus to invade successfully. The emergence of a new strain of meningococcal bacteria in the Czech Republic provides a good example of this phenomenon. Against a background of stable and nonoverlapping combinations of antigenic variants at three immunodominant loci circulating in the meningococcal population in the 1970s and 1980s, a new lineage emerged in the population in 1993 expressing previously unobserved antigenic variants at all three loci in our study (PorA VR1, VR2, and FetA), rising to a relatively high prevalence and causing significant amounts of disease (12).

The dynamic implications of the stochastic model framework extend also to such pathogens as influenza, in which strains appear to emerge sequentially along a diagonal pathway through antigen space (30). The exploration of strain space by the pathogen population in our simulations follows a trajectory in which new strains can successfully emerge only when they acquire different alleles (or variants) at all loci (or epitope regions). This behavior is consonant with models of influenza that either rely on restrictions on epitope diversity within a discrete framework, as suggested by Recker et al. (31), or propose a more continuous structure to strain space with cross-immunity decaying along a number of different epitope axes (32). Such factors as short-term cross-immunity (33) are likely to reinforce this behavior and, together with a high level of redundancy in genotype-phenotype mapping (34), may be necessary to generate the phylogenetic patterns characteristic of influenza. An important future direction for this work will be to explore the relationship between these model frameworks and phylogenetic data for a variety of other pathogen systems.

Methods

Deterministic Model.

The model is a direct extension of the one introduced by Gupta et al. (6) incorporating asymmetric numbers of alleles. Here, pathogen strains are defined by up to three immunodominant loci, a, b, and c, with i, j, and k alleles, respectively: a₁…a_i, b₁…b_j, and c₁…c_k. This allows for a maximum of i*j*k different combinations of alleles that constitute a strain. The host population is divided into three partially overlapping compartments for each strain s: the proportion infectious with strain s, y_s; the proportion immune (here, infected or previously exposed) to strain s, z_s; and the proportion immune to any strain that shares alleles with s, w_s. The rate of change in these compartments is given by the following set of differential equations:

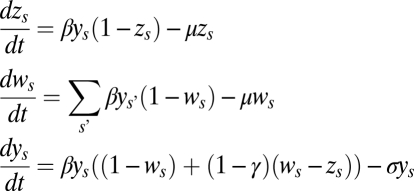For simplicity, it is assumed that sharing one allele has the same protective effect as sharing more than one. The strength of cross-immunity is determined by the parameter γ, and all strains are assumed to have the same transmissibility, β. The duration of infectiousness is 1/σ and is short compared with the average lifespan 1/μ, (i.e., σ>>μ); immunity is assumed to be lifelong. R₀, the basic reproduction ratio of a strain, is simply given by β/σ. Recombination is not explicitly modeled, and all possible strains are present from the start.

Stochastic Model.

An individual-based stochastic model was also developed, in which a population of hosts is infected by a directly transmitted and antigenically diverse pathogen species. Hosts are connected to each other on a dynamic random-mixing network (26), which is seeded randomly with different strains of the pathogen. Hosts remain infectious (for a period 1/σ, on average, where σ is the rate of loss of infectiousness) before recovering and maintain allele-specific immunity for a given duration after this (1/ς, on average, where ς is the rate of loss of immunity). Pathogen strains are defined by antigenic alleles at either two or three loci. Each locus has a defined number of alleles, such that strain space may be envisaged as either a 2D matrix or a 3D rectangular box of allelic associations. Infection with each strain generates allele-specific immunity within the host. The susceptibility of a host to infection by a new strain is then dependent on how many alleles it shares with previously seen strains as well as its transmissibility, similar to previous models (6, 26). It is assumed that all strains are equally transmissible, and two strains coinfecting the same host could undergo recombination with a defined probability. In addition, each locus is subject to mutation, allowing for all possible areas of strain space to be explored during a simulation and every strain to emerge if it could be competitive. Table S1 shows the range of parameters explored. A total of 2,500 simulations were run in which the pathogen population is defined by three loci with 3, 4, and 5 alleles, respectively, just as in the deterministic model. This yielded a strain space described by a 3 × 4 × 5 matrix of allelic associations. A further 3,600 simulations were run for a two-locus model, 1,000 with a symmetric number of alleles (5 at each locus), 600 with 2 alleles at one locus and 5 alleles at another, and 2,000 with 10 alleles at one locus and 25 alleles at another. These simulations explored the effects of increased numbers of alleles, as well as changing host population size. To explore spatial effects within the host population and the impact of population size, we ran 7,000 simulations with varying host contact network structure and population size, as described in SI Text.

Metrics for the Evaluation of Diversity and Discordance.

To describe the pathogen population, we used a measure of diversity (D) based on the Shannon–Weaver index of diversity, previously used for this kind of system (26). This measure describes how evenly the pathogen population is distributed across all possible strains and is given as

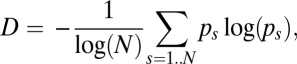where N is the total number of possible strains and p_i is the proportionate prevalence of strain i in the population (i.e., p_s = y_s/y with).

In addition, a metric for discordance or lack of overlap, f*, was used to measure the extent to which pathogen strains share alleles (12). Discordance can be calculated by evaluating the mean “dominance” of the most prevalent composition of a particular allele averaged over all alleles, where dominance refers to the relative prevalence of strains expressing particular allelic combinations. That is, for each allele i (or j or k), we find the most prevalent strain containing allele i and calculate its dominance over all other strains containing this particular allele. In the context of a two-locus system, this can be understood as calculating the “row” and “column” dominance for each allele within a matrix of allelic associations; in the three-locus model, we also take into account each allele's relative dominance with respect to all three axes (row, column, and “depth” within a 3D box of allelic associations). As a three-locus example, let a₀b_jc_k be the most prevalent of all strains containing allele a₀. Its dominance compared with all other strains containing a₀ or b_jc_k can be calculated as

As the averaged mean of all alleles, f* is then given as

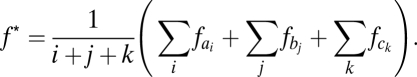Therefore, f* scores close to 1 indicate that combinations of alleles at three loci share very few alleles, whereas lower scores are indicative of overlapping associations.