The modelling of a primitive ‘sustainable’ conservative cell

Abstract

The simple sustainable or ‘eternal’ cell model, assuming preservation of all proteins, is designed as a building block, a primitive element upon which one can build more complete functional cell models of various types, representing various species. In the modelling we emphasize the electrophysiological aspects, in part because these are a well-developed component of cell models and because membrane potentials and their fluctuations have been generally omitted from metabolically oriented cell models in the past. Fluctuations in membrane potential deserve heightened consideration because probably all cells have negative intracellular potentials and most cells demonstrate electrical activity with vesicular extrusion, receptor occupancy, as well as with stimulated excitation resulting in regenerative depolarization. The emphasis is on the balances of mass, charge, and of chemical species while accounting for substrate uptake, metabolism and metabolite loss from the cell. By starting with a primitive representation we emphasize the conservation ideas. As more advanced models are generated they must adhere to the same basic principles as are required for the most primitive incomplete model.

1. Introduction

Genomics, molecular and cell biology have evolved so rapidly in the past few years that there is more information available than can be readily or accurately understood in terms of the behaviour of whole cells, intact tissues and organs, and of the functioning organism. Even where the biochemical pathways are known, it is not yet possible to fully portray the fluxes along them, or their regulation over a physiological range of conditions. Yet these and a host of related functions, at all levels of integration, are just what are required in order to understand and predict the effects of genomic or pharmacological intervention (Schilling & Palsson 2000). Because even small systems are sufficiently complex, nonlinear, and time-varying, intuitive understanding is impossible. The present and proposed modelling, at the cell and subcellular levels, has the purpose of providing computational models as mind-expanders, as aids to intuition, and as a means of developing a feeling for and a quantitative appraisal of complicated networks of reactions, transport processes, receptor signalling, etc., in a functioning cell.

This limited goal, the provision of knowledge at the cellular functional level, is important in its own right as a vehicle for understanding drug interactions, as in cardiac arrhythmias, or receptor blockage. Moreover, it is one of a set of goals aimed towards understanding the larger systems at the organ level, e.g. cardiac contraction and ejection fraction and contractility, and at the organism level, e.g. blood pressure and volume regulation, or endocrine regulation.

The reader may feel that the goal of defining the primitive sustainable ‘eternal’ cell is too modest to be worthy of phrasing as a meaningful stepping stone, but it does define a real goal on the way toward higher-level systems integration (Bassingthwaighte 2000). The purpose of this essay is not to report that such a goal has been achieved, for it has not, but to try to define the route toward this goal and to report on the progress that has been made toward it.

(a) The ‘eternal’ cell

Pretend that there are no proteolytic enzymes, no protein degradation, and that no energy goes into protein production. All protein concentrations are constant. There is no potential for cell division, or for changes in gene expression. In this parsimonious situation, in this ‘eternal’ cell, one can work out the basics of what a simplified but functioning cell requires to sustain function. Such models pose as minimal standardized cell models, properly conservative in a biophysical and energetic sense, and need to account for dissipative losses by metabolizing substrates. A sequence of more complex and more interesting tissue and organ models can be constructed from them.

The cell membrane is permeable, so that sustaining the cell requires energy or substrate from outside. The elemental functions are (1) to sustain a transmembrane potential, E_m, in the resting state, in spite of leakages of ions across the cell membrane; this requires being able to recover the ionic balance after an action potential in an excitable cell, and to maintain the cell’s ions and the E_m, and to maintain electroneutrality; (2) to maintain the energy balance, primarily in high-energy purine nucleotides and high-energy phosphates; (3) to support a more or less steady state for the redox state (reducing equivalents), and for pH, osmolarity, cell volume, and for the concentrations of substrates and metabolites.

We take a conservative approach, in the sense of trying to make sure that all of these balances are expressible in terms that allow calculation of the costs and mechanisms of maintaining a steady state. Consider a finite system: enclose the cell within a finite volume of extracellular fluid, and then account for all solutes and solvents exchanging between the cell and its surrounding fluid space. This allows mass balance to be calculated. If the extracellular volume is much larger than the cell, then substrates and oxygen will be only gradually depleted, and the metabolites will accumulate gradually.

A computational model of this primitive cell allows one to determine the minimal requirements for supplying substrate from outside the system to sustain a true steady state inside a cell with precisely defined ion and substrate fluxes. Questions such as the following can be addressed. Can one sustain the cell with glucose alone if there is no need for protein production? What are the enzymes required to maintain ATP balance given that there is metabolism of adenosine? Are the kinetic rate constants, equilibrium constants, and forward reaction velocities reported in the literature compatible with sustaining the cell? What are the thermodynamic constraints that limit the possible range of kinetic rate constants?

2. Modelling to define the balancing act

The conservative cell in the steady state is in balance. Parasitic beasts that we are, every cell requires some source of energy, a minimal set of substrates supplied from outside, and produces a set of metabolites. The metabolites would, if not removed from the cell, eventually poison it. Therefore, every cell model needs to incorporate these inflows and outflows. Our most primitive cell model is no exception, but pretending that there is no proteolysis allows us to omit major components of a real cell: the nucleus and the genes, transcription and regulation of the transcriptome, cell division, protein synthesis, recognition and signalling pathways, and even such details as the anaplerotic and cataplerotic exchanges with the tricarboxylic acid cycle. We need to account for the regulation of enzymes. In this basic approach we take advantage of the prior modelling developments in single cell modelling. The lowest level version needs to incorporate ionic channels and pumps, and transporters for the essential substrates that cannot readily diffuse across lipid bilayers. The cell model should account for ionic fluxes and potentials, energy (cellular free energy, redox state), transient and steady states in substrate and metabolite concentrations and in pH, balances for key atoms (C, N, P, S, O), water and osmolarity balance.

3. Ionic balances and imbalances

(a) The pumps and exchangers

If only the alkali metal ions required governance, then the minimum three ionic pumps would be the NaK ATPase, the Ca ATPases on the cell membrane and on internal membranes, and the Na/Ca exchanger, extruding Ca or Na depending on the circumstances. But to preserve H⁺ ion levels, the NaH exchanger is needed too. So the main four are:

1. NaK ATPase: 3 Na⁺ outward for 2 K⁺ inward; electrogenic, uses ATP, polarizing;

2. Ca ATPase: 2 Ca²⁺ from cytosol for 1 ATP → ADP;

3. Na/Ca exchanger: 3 Na⁺ in for 1 Ca²⁺ out, electrogenic, depolarizing, no ATP required;

4. Na/H exchange: 1 Na for 1 H⁺, electroneutral, and the Na/HCO₃ cotransporter.

Some cells do not have all of these. For example, dog erythrocytes lack an NaK ATPase: their intracellular [K⁺]_i level is low; the intracellular [Na⁺]_i is nevertheless only ca. 40 mM while [Na⁺]_o is still 140 mM, a consequence of the combined effects of the efficacy of the Na/Ca exchanger and the plasmalemmal Ca ATPase. In this case the Na/Ca exchanger is powered by the [Ca²⁺] gradient, driving Na out at the expense of Ca influx on the exchanger. In effect, the Ca ATPase is doing all the work. One genus of sheep has red blood cells (RBCs) of two types, one with the Na pump and one without (Hoffman & Tosteson 1971).

Cooling a cell to low temperatures stops all the pumps. Then Na_i accumulates, but heart cells maintain a low enough permeability to Ca that they do not go into contracture. On rewarming, the pumps restart, and work so effectively that the membrane potential may be driven to hyperpolarizing levels (Hiraoka & Hecht 1973). We (Bassingthwaighte et al. 1976) observed hyperpolarization even to lower than −120 mV in the course of experiments on how high Ca_i raises the conductance of the potassium channels.

Regulation of pH is vital for stable metabolism. The Na/H exchanger is one of a set of transporters involved in pH balance. The Na/HCO₃ co-transporter (Dart & Vaughan-Jones 1992) is argued to be electrogenic (Aiello et al. (1998) say yes; Choi et al. (2000) say no) and there are two other transporters involved with pH balance, the Cl/HCO₃ exchanger and the Cl/OH exchanger (Leem & Vaughan-Jones 1998a, b).

The pumps and exchangers cause net movement of charges, so they contribute to both the membrane potential and to the shape of the action potential. This can be illustrated with the model of Winslow et al. (1999), and with that of Noble and co-workers (see, for example, Noble et al. 1998; Ch’en et al. 1998), the Oxsoft Heart model, which is available commercially and also through collaboration with its creators (www.oxsoft.co.uk).

(b) Nernst potential

This is the potential difference across a membrane due to a difference in the concentration of a particular ion on the two sides. There is a Nernst potential for each charged molecular species.

Potassium concentration inside, [K⁺]_i, is, for example, ca. 140 mM and outside is 4 mM. Its Nernst potential, E_K, is

$$E_{\mathrm{K}}=\frac{\mathit{\text{RT}}}{\mathit{\text{zF}}}\text{log}\frac{{\mathrm{K}}_{\mathrm{o}}}{{\mathrm{K}}_{\mathrm{i}}},$$ (3.1)

where R is the gas constant (8.314 J mol⁻¹ K⁻¹), T is temperature (kelvins), z is valence of the ion and F is Faraday’s constant (98 485 C mol⁻¹). The ratio RT/E_mF is the ratio of thermal energy to electrical energy. The Faraday constant is equal to the charge on an electron, e (in coulombs), times the number of ions per mole, N_A, Avogadro’s number, so

$$\frac{\mathit{\text{RT}}}{F}=\left[\frac{\mathit{\text{RT}}}{N_{\mathrm{A}}e}\right]=\left[\frac{k_{\mathrm{B}}T}{e}\right],$$ (3.2)

where k_B is the Boltzmann constant, which is equal to the gas constant R divided by N_A, and e is the energy in joules of an ion per kelvin.

1. At 37 °C (= 310 K), then RT/zF times log_e, 10 (which is 2.303) is 61.3 mV, so that E_K = −94.6 mV.

2. With Na_o = 145 mM, Na_i = 15 mM, E_Na = +60 mV.

3. With Ca_o = 2 mM, Ca_i = 10⁻⁷ M, E_Ca = +129 mV.

4. With Cl_o = 120 mM, Cl_i = 5 mM, E_Cl = −83 mV. But equilibration is fast, and is in accord with the intracellular protein concentrations, so it has little or no effect on the membrane potential, E_m.

(c) Resting potential E_R, or E_m in the absence of an action potential

If potassium were the only ion for which there was a conducting pathway across the membrane, then E_m would be E_K. But it is not, so other influences must coexist. The resting potential is governed by all the leaks and pumps that allow or drive net charge flow. The Goldman–Hodgkin–Katz expression (Goldman 1943; Hodgkin & Katz 1949; Sperelakis 1979) accounts for the conductances due to the leaks:

$$E_{\mathrm{m}}=-\frac{\mathit{\text{RT}}}{F}\text{log}\frac{P_{\mathrm{K}}{\mathrm{K}}_{\mathrm{i}}+P_{\text{Na}}{\text{Na}}_{\mathrm{i}}+2P_{\text{Ca}}{\text{Ca}}_{\mathrm{i}}}{P_{\mathrm{K}}{\mathrm{K}}_{\mathrm{o}}+P_{\text{Na}}{\text{Na}}_{\mathrm{o}}+2P_{\text{Ca}}{\text{Ca}}_{\mathrm{o}}},$$ (3.3)

where the Ps are the permeabilities for the individual ions. The terms are proportional to the fluxes: each unidirectional flux z_XP_XX · E_mF/(RT(1 − e^−E_mF/RT)) is a unidirectional flux of ion X per unit surface area of the membrane, where z_x is the valence, X is the concentration of the ion on one side or the other and represents [X]_{i or o} and the phrase E_mF/(RT(1 − e^−E_mF/RT)) is a factor to account for the electrical field (assumed constant) within the membrane channel or pore. Since it is the same for all terms, it cancels out of the numerator and denominator. When E_m is near zero the term E_mF/(RT(1 − e^−E_mF/RT)) goes to 1.0. The multiplication of the Ca flux by 2 is because the valence is 2, and two charges are carried. The subscripts ‘i’ and ‘o’ indicate inside and outside. The chloride concentration difference does not influence E_m because it is strictly passive and equilibrates in accord with the potential determined by the ions which are pumped and electrogenically exchanged. Blocking the leaks for K⁺ and Ca²⁺ will allow P_Na to become the dominant leak, and then E_m goes to E_Na.

(i) Modification of the Goldman–Hodgkin–Katz equation for pumps

The pumps and exchangers are operating continuously, and will have an influence if the currents they carry are of the same magnitude as the leaks. Consider each component as a flux, i.e. P_KK_i is the unidirectional flux of a charged species, potassium, with the units millimoles per second per square centimetre of surface area. The right term of the Goldman equation is a ratio of currents. The NaK pump current can be represented by a net efflux of monovalent cations, J_ep, multiplied by the reciprocal of the scalar E_mF/RT accounting for the effect of the constant intramembrane field on the Ps. Ignoring the Ca fluxes, which are small at the resting potential, we rewrite the expression:

$$E_{\mathrm{m}}=-\frac{\mathit{\text{RT}}}{F}\text{log}\frac{P_{\mathrm{K}}{\mathrm{K}}_{\mathrm{i}}+P_{\text{Na}}{\text{Na}}_{\mathrm{i}}+J_{\text{ep}}\mathit{\text{RT}}/(E_{\mathrm{m}}F)}{P_{\mathrm{K}}{\mathrm{K}}_{\mathrm{o}}+P_{\text{Na}}{\text{Na}}_{\mathrm{o}}}.$$ (3.4)

Other pumps can be represented similarly. Alternative approaches are given in the chapter by Sperelakis (1979).

(d) Time- and voltage-dependent leak currents

Nerve and muscle cells were the first to be recognized to be excitable, responding to electrical excitation. Cardiac cells were found to generate waves of depolarization at regular intervals, spontaneously, as seen in the electrocardiogram (ECG). The electroencephalogram showed that similar events were going on in the brain. Now we know that many other cells are excitable, some in association with cell motion, some in association with extrusion of material from the cells, for example the pancreatic beta cells, secreting insulin, and the mast cells, extruding histamine. For our exemplary cell, we will incorporate the channels associated with time- and voltage-dependent ionic conductances, even while recognizing that some cells will not express all those channel proteins found in the heart or brain. Non-excitable cells lack the regenerative depolarization served by a Na⁺ or Ca²⁺ channel, but do have K⁺ channels. Several models have been worked out over the past half century. See Noble & Rudy (2001).

(e) The pumps and exchangers influence the action potential

The NaK ATPase, the Ca ATPase and the Na/Ca exchanger are all electrogenic and therefore influence both the resting potential and the action potential. The two ATPases are ‘demand’ pumps: they pump more when there is more to pump, and the work they do per ion transferred is dependent on the transmembrane potential. The pumps are reversible and the ionic gradients can be used to produce ATP from ADP: Makinose & Hasselbach (1971) showed this for the Ca ATPase on the sarcoplasmic reticulum, and it is true for the NaK ATPase as well. The Na/Ca exchanger depends upon the electrochemical potential for Na⁺ as the driving force for the extrusion of Ca²⁺. It can work in either direction, to extrude calcium using the Na⁺ gradient as the energy source or to use the Ca²⁺ gradient to extrude Na⁺. The general rule is that all enzymatic reactions and pumps are reversible, given that the laws of thermodynamics are not violated.

The influences during a single action potential can be explored with the action potential model of Winslow et al. (1999) on our website (http://nsr.bioeng.washington.edu) or with the Oxsoft model (www.oxsoft.com). Reversal of the Na/Ca exchanger current occurs during the plateau phase of the action potential. The Na/Ca exchange current gives net positive charge flux inward at the resting potential. However, during the plateau of the action potential this is reversed. Likewise, a reduction in the flux via the NaK ATPase changes the action potential, due to the reduction in the net outward current (3 ions Na out for 2 ions K in).

(f) Electroneutrality

Despite all the rapid changes in the membrane potential the cell remains essentially electroneutral, the changes in E_m representing minuscule fluctuations in the number of ions of one charge or the other in excess. The electroneutrality means that the sums of the negative and positive charges must balance. The governing equation is

$$0={\displaystyle \sum }{z}_i{C}_{\text{anions}}+{\displaystyle \sum }{z}_i{C}_{\text{cations}}.$$ (3.5)

In actual practice, because the number of ions of Na entering with each action potential is only 1/10⁷ times the [Na]_i, this equation cannot be readily used to calculate changes in charge balance and in the membrane potential without going to higher precision arithmetic.

Stabilizing influences are osmotic water balance and the protein content of the cell. Generally, the membrane is impermeable to proteins, which are usually negatively charged, the more highly charged ones having more histidines and lysines. These negatively charged groups on the surface attract cations and repel anions. They contribute immensely to the ionic and osmotic balances within the cell. Since the proteins, at least in our hypothetical conservative cell, do not leave the cell, they are a major component of the anions and thus intracellular chloride is much lower than extracellular. There is a Donnan equilibrium, or a Gibbs–Donnan potential.

(g) The Gibbs–Donnan potential

Consider that the concentration of the negative charges on the protein is, for example, 100 mM, with the charges counterbalanced by Na⁺. If Na⁺ and Cl⁻ are both freely diffusible through the membrane, but proteins not, and there is an outside NaCl concentration of 100 mM, then two conditions must be reached: (1) electroneutrality both inside and out, and (2) zero steady state net flux of ions.

Under these conditions:

$$\frac{{[\text{Na}]}_{\mathrm{i}}}{{[\text{Na}]}_{\mathrm{o}}}=\frac{{[\text{Cl}]}_{\mathrm{o}}}{{[\text{Cl}]}_{\mathrm{i}}},$$ (3.6)

and

$${\displaystyle \sum }{[\text{protein}]}_{\mathrm{i}}+{[\text{Cl}]}_{\mathrm{i}}={\displaystyle \sum }{[\text{bound Na}]}_{\mathrm{i}}+{[\text{free Na}]}_{\mathrm{i}}.$$ (3.7)

If the volumes inside and outside are equal then the outside concentrations of Na and Cl are depleted to balance the protein charges inside the cell, settling at [Na]_o and [Cl]_o both equal to 67 mM while [Na]_i = 133 mM and [Cl]_i = 33 mM. This gives a ‘Donnan’ potential equal to the Nernst potential for either Na⁺ or Cl⁻ of −18 mV. Notice the big difference in total concentrations on the two sides of the membrane: this gives rise to an osmotic gradient, a driving force for water flux. This Gibbs–Donnan idea is therefore an incomplete model unless water cannot cross the membrane, or unless there is a large intracellular pressure excess across the membrane to offset the osmotic imbalance.

(h) Excitation–contraction coupling

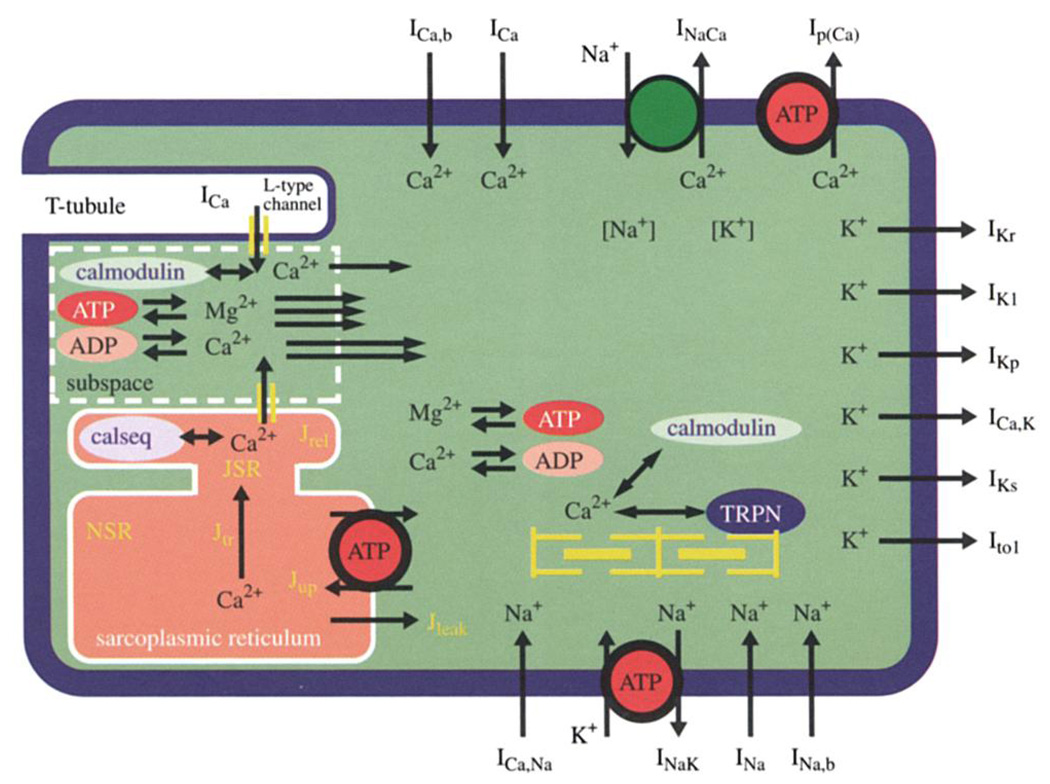
The processes involved in excitation–contraction (EC) coupling are relevant to a host of events in cellular biology. These include the elevation of Ca_i that induces the release of Ca from intracellular storage sites, and Ca binding to proteins that lowers its effective diffusion coefficient. (Ca triggers other events (motility of proteins, vesicular transport and exocytosis), affects various signalling pathways, and causes shifts in metabolism not only of substrates for energy generation but also of pathways for cellular responses to injury, stress, etc., leading to changes in gene expression and regulation of the proteome, but we do not consider these in our most primitive cell. We define the proteome as the status of all the proteins in the cell.) Figure 1 provides an overview of the mechanisms.

Figure 1.

Diagram of the pumps, leaks and voltage-dependent channels in the cardiac myocyte. (Representing the ionic currents, pumps, and exchanges in the model by Winslow et al. (1999) and from Michailova and McCulloch at the University of California in San Diego, the calcium and magnesium binding to ADP and ATP, to myofilament proteins, and to carrier proteins calsequestrin (inside SR) and calmodulin (cytosolic).) The simple arrows across the membrane are channels; the circles in the membrane are ‘pumps’ when powered by ATP and are exchangers when powered by the transmembrane electrochemical potential differences. Other ionic fluxes in an excitable muscle cell are indicated. Specific action potential models can be found on Web sites. The models of Hodgkin & Huxley (1952), Beeler & Reuter (1977) and Winslow et al. (1999) can be run and parameters changed at http://nsr.bioeng.washington.edu. The Luo–Rudy model is at http://www.bme.jhu.edu/~nthakor/Lab/cardio/isc_mod; the model of DiFrancesco & Noble (1985) is at http://cmrg.ucsd.edu; the Oxsoft model (Noble et al. 1998; Kohl et al. 1999) is at www.oxsoft.co.uk.

For EC coupling the sequence of events is as follows:

1. electrical depolarization (using only small numbers of ions to make large changes in transmembrane voltage);

2. geometrically selective points of entry of the calcium inward current into the SR-subsarcolemmal opposition space (Bassingthwaighte & Reuter 1972) occurring during the plateau of the action potential introduces ‘trigger’ Ca, which in turn induces release of Ca from SR;

3. Ca diffuses into myofilament bundles;

4. binds to troponin-C allowing contraction; and

5. relaxation of the muscle occurs when Ca is removed from the cytosol and from the myofilament space by the Ca ATPase pump on the SR membrane, priming it for the next release.

(i) Mechano-electrical feedback

Kohl et al. (1998, 1999) and Kohl & Sachs (2001) have added this to the Oxsoft model. Stretch can induce shortening or lengthening of the action potential. The evidence points to changes in K⁺ channel conductance as being the basis, but the molecular mechanism is not clear.

(j) Energy balance in the cell

What is the measure of the energy balance? How is a balance achieved? What are the consumers and producers of energy? In our hypothetical cell not requiring protein expression, it is possible to model the balancing events. We start with a mathematical cell, in order to minimize the number of biochemical reactions to be considered. Again pH comes into the picture for it plays a vital role in relating the biochemical and energetic reactions. An RBC is a simple cell that has been modelled well (Joshi & Palsson 1990; Mulquiney & Kuchel 1999a, b; Mulquiney et al. 1999; Church & Palsson at http://arep.med.harvard.edu), for it has no mitochondria, no fatty acid metabolism, and no protein production, but requires energy for the pumps.

Much work is going into E. coli. Karp et al. (1999) have developed an extensive database of enzymes and reaction schema for the pathways; Savinell & Palsson (1992), Pramanik & Keasling (1997), Schilling et al. (1999a, b, 2000) and Schilling & Palsson (2000) have developed both theory and extensive models.

The E-CELL project of Tomita et al. in Japan (see Tomita et al. (1999), http://www.e-cell.org/ and Kitano (2001)) tackles the cell from another point of view, namely, what is the minimum number of genes that can be selected to maintain a cell population, allowing transcription, translation, but not cell division? Remarkably, only 127 genes allow a maintainable system, but obviously this would not account for very much of the biology of the everyday working cell.

(i) Cellular free energy

Focusing on ATP at the energy store, the Gibbs free energy of ATP hydrolysis, ΔG, is given by

$$\mathrm{\Delta }G=\mathrm{\Delta }{G}^0+\mathit{\text{RT}}\text{ln}\frac{[\text{ADP}][P_{\mathrm{i}}]}{[\text{ATP}]},$$ (3.8)

where the ratio of concentrations is related to the high-energy phosphorylation potential, E_ph,

$$E_{\text{ph}}=-\frac{\mathit{\text{RT}}}{F}·\text{ln}\frac{[\text{ATP}]}{[\text{ADP}][P_{\mathrm{i}}]},$$ (3.9)

calculated from the cytosolic concentrations of free, unbound ATP, ADP, and inorganic phosphate. E_ph is normally ca. −65 mV. Values more negative indicate higher energy reserve. At −45 mV the cell stalls for lack of energy. The high-energy phosphorylation potential is approximated well by the adenine nucleotide situation since the ADP and ATP are nearly in equilibrium through the myokinase reaction, are nearly in equilibrium with phosphocreatine, PCr, through the creatine kinase reaction, and are in high concentrations relative to other high-energy phosphates.

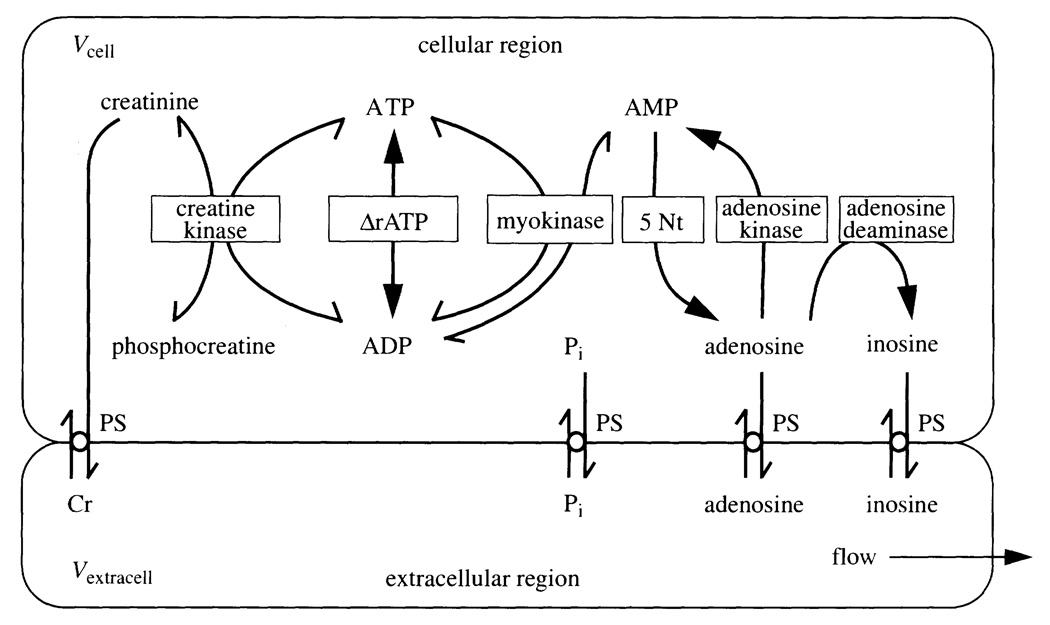
A diagram of a part of the nucleoside/nucleotide reactions (figure 2) shows a narrowly limited set of the reactions in which ATP is involved. Palsson’s modelling of E. coli metabolism accounts for over 200 reactions involving ATP. Our diagram is focused on the central reactions through which the major regulation occurs. Though this essay focuses on the sustainable cell, in real life the communication between cells of different types governs cell behaviour all the way from gene expression to immediate physiological responses.

Figure 2.

Nucleotide and nucleoside reactions in the myocardium. Myocyte and endothelial cells both play a role in regulating the interstitial adenosine concentration and its occupancy of receptors on the smooth muscle cell (from Kroll et al. 1997).

(ii) Energy consumers

The obvious consumers of ATP are the kinases; the phosphatases lyse phosphorylated compounds and thereby degrade what kinases formed. There are many others, at all levels, from transcription to transporters. The biggest consumers are the pumps and contractile proteins. Kinases use ATP at the entry points in the substrate metabolic pathways; e.g. both glucose and fatty acids are phosphorylated, using ATP, before they can be metabolized to provide more ATP. In some cases, this ‘down payment’ is sufficiently disadvantageous that at least one organism, the trypanosome, has developed a sequestered vacuole, the glycosome, within which the kinase operates during recovery from hypoxia to prime the pump before depleting the last of the available ATP. Without sequestering the enzymes for glycolysis the cellular ATP can be completely depleted when the organism is resupplied with oxygen, causing its death even while in an environment conducive to recovery (Bakker et al. 2000). Contractile cells such as cardiac myocytes normally expend most of their energy on contraction, ca. 50% of ATP hydrolysis being used by myosin ATPase, ca. 20% for ion cycling and the remainder for cell maintenance (Gibbs & Chapman 1979). These proportions can change dramatically. While the cell seems to protect itself against contractile demands that exceed oxygen availability by stopping contraction, the protection against demands for ATP by the pumps is incomplete: when high Ca²⁺ influx occurs, as in halothane-induced malignant hyperthermia or by the administration of a calcium ionophore, the activity of the Ca ATPase can quickly deplete the cell of virtually all of its ATP (Rohn et al. 1996).

(iii) Energy producers

The basic substrates for ATP production are sugars and fats, though amino acids are normally consumed as well. Energy production from all three types of substrate is mainly through the tricarboxylic acid cycle. Only in the RBC is glycolysis alone sufficient to supply the cell’s energy. A first version of a conservative cell could be based on glucose metabolism alone. Erythrocytes and neurons are almost solely powered by glycolysis, and endothelial cells mainly, but most cells use varied proportions of sugar, fat and, to a lesser extent, protein. From glucose, C₆H₁₂O₆, the stoichiometry for glycolysis (from glucose to pyruvate) is

$$2\text{NAD}+1\text{glucose}+2\text{ATP}\to 4\text{ATP}+2\text{pyruvate}+2\text{NADH}$$

and for the overall reaction including the intramitochondrial oxidation:

$$\text{ADP}+P_{\mathrm{i}}+\text{NADH}+\text{FADH}+1\text{glucose}+6{\mathrm{O}}_2\to 36\text{ATP}+6{\text{CO}}_2+\text{NAD}+\text{FAD}.$$

These are not exact stoichiometries, for the exact numbers depend on how the NADH reducing equivalents are transferred from cytosol to intramitochondrial space: via a malate–aspartate or glycerophosphate shuttle. With the former the yield is 38 ATP per glucose, 36 with the latter. Likewise there is some cost for transmembrane transport of glucose, i.e. for manufacturing the transporters. In any case, glucose oxidation yields about 6 ATP per O₂. Fatty acid oxidation, somewhat more complex, but sharing the same tricarboxylic acid cycle (the TCA cycle), gives a similar yield, about 5.6 ATP per O₂ (Bassingthwaighte 1991):

$$1\text{palmitic acid}+23{\mathrm{O}}_2\to 129\text{ATP}.$$

The regulation of the balance between fatty acid and glucose varies among different cell types. Regulation occurs in exercising muscle via malonyl CoA (Kudo et al. 1995). While it is well known that the muscle of sprinters is dominantly fast twitch, glycolytic type, and that of marathoners is slow twitch, depending more on fatty acid (see, for example, Andersen et al. 2000), and that one muscle type can be gradually converted to another by a change in muscular activity (Buller et al. 1960a, b), how this major regulatory shift occurs is not known. It does involve changes in gene expression, as the myosin isoforms differ in the different athletes.

When cardiac muscle is unloaded there is a shift away from glucose utilization (Depre et al. 1998). When hypoxia is such that the oxygen supply is compromised, fatty acid oxidation and the TCA cycle are slowed. There is a strong shift to glycolysis, the pyruvate is converted to lactate, and the cell goes into survival mode, ceasing contraction, but maintaining viability on the net production of 2 ATPs per glucose. Here the Na/H exchanger and also the Na/HCO₃ cotransporter both operate to reduce the raised intracellular pH (Lagadic-Gossmann et al. 1992). A complete modelling should include Pasteur and Crabtree effects, which may vary between cell types (Racker 1980).

The regulation of metabolism is complicated, and has led to the development of the field of metabolic control analysis (MCA). Following leads from Kacser & Burns (1973) and Newsholme & Start (1973), the field has evolved to provide the tools for gaining insight into complex systems and for designing approaches to control via intervention. One should distinguish three key approaches. The first of these theories is flux-orientated theory (FOT), summarized by Crabtree & Newsholme (1985). The second, metabolic control theory (Kacser & Burns 1973), is summarized in a book by Fell (1996). The third is biochemical systems theory, put forward by Savageau and others (see, for example, Sorribas & Savageau 1989). Savageau’s theory assumes that finite power equations can be used instead of differentials to represent metabolic reactions. Metabolic control analysis (MCA) and FOT are both based on differential coefficients, with the former relying on ‘control theorems’ (see, for example, Cornish-Bowden 1989). None of these methods of analysis is easy to apply, but they provide higher levels of insight into the system since they provide something closely akin to sensitivity analysis. The difference between MCA and FOT is the reliance in the former on changes in enzyme activity, while in the latter, the focus is on changes in regulator concentrations. While MCA provides ways of looking at systems in steady state, it gives strong inferences about the responses to increases in demand at particular points in reaction networks. These are expressed in terms of elasticity coefficients and control coefficients. The elasticity coefficients are the logarithmic slopes of the relationships between concentration and fluxes; control coefficients are the ratios of the proportional change in a flux of a substrate divided by the proportional change in the substrate concentration. A point emerging from the theories is that systems are governed mainly by demand, not supply.

It is possible to simplify the computation of complex metabolic networks and still represent the kinetics faithfully for specific states. Palsson et al. (1987) used low-order linear differential operators to replace linear reaction sequences, thus capturing the timing of the mass flux through the set of reacting species within the sequence. This is very efficient but what is lost is the flexibility and automatic nature of the regulation as conditions change. Now he uses the fully detailed set of reactions, resulting in large computations (Schilling et al. 2000), something that was not possible 15 years ago.

A critical requirement in formulating models of networks of reactions is to appreciate that in principle all reactions are reversible: high product concentrations produce substrate, running the reaction backward. This holds for the ionic pumps: driving the SR ATPase backwards produces ATP when ADP is available as substrate. For a reversible Michaelis–Menten (M–M) reaction the flux from substrate to product may be written (see, for example, the book by Westerhoff & Van Dam (1987)):

$$J_{S,P}=\frac{(V_{\mathrm{f}}S)/k_S-V_{\mathrm{r}}(P/k_P)}{1+S/k_S+P/k_P},$$ (3.10)

or

$$J_{S,P}=(1-\frac{\Gamma }{K})\frac{V_{\mathrm{f}}(S/k_S)}{1+S/k_S+P/k_P},$$ (3.11)

where S is substrate concentration, P is product, the net forward reaction J_S,P may be negative or positive, V_f is the rate of the forward reaction, V_r that of the reverse or backward reaction, K is the ratio of P to S at equilibrium and equals (V_f/k_S)/(V_r/k_P), k_S is the dissociation constant for S from the enzyme, k_P is the dissociation constant for P from the enzyme, and Γ is the ratio of P to S at any time. When Γ = K the reaction is at equilibrium. When P is zero this reduces to the standard M–M relationship for the forward reaction S → P. This equation is simpler than is necessarily the case: it assumes equilibrium dissociation of both substrate and product in their binding with enzyme, and that the reaction step, in either direction, is slow compared with the association/dissociation rates. The virtue of its use compared with the standard M–M equation is that networks of such reactions are more stable than those assuming irreversibility: concentrations do not go to zero. Furthermore, the reversibility imposes a thermodynamic constraint that limits the effective range of possible values for the kinetics, as shown, for example, by Gresser (1983), and which is summarized at an equilibrium between forward and backward reaction velocities by the Haldane relationship (Mahler & Cordes 1971).

Similar consideration needs to be given to the reversibility of reactions which show cooperativity, and for the same reasons. Mathematically, this was more difficult to handle until Hofmeyr & Cornish-Bowden (1997) worked out a minimally complex version of the reversible Hill equation:

$$J_{S,P}=\frac{(V_{\mathrm{f}}S/k_S)(1-\Gamma /K){(S/k_S+P/k_P)}^{n-1}}{1+{(S/k_S+P/k_P)}^n}.$$ (3.12)

The exponent n is a descriptor for the degree of cooperativity, greater than 1 for positive cooperativity. The exponent does not take high values, and is about 2.7 when there is cooperativity for binding at four sites, as for oxygen binding to haemoglobin. Nevertheless, a steep relationship between concentration and flux does make for increased responsiveness to concentration changes and reduces stability.

Another mechanism for increasing the steepness of stimulus–response relationships is partial sequestration of the enzyme. Thomas & Bassingthwaighte (2000) show that when access of substrate to the active site is hindered, the relation between the reaction forward flux versus concentration may have a very high apparent Hill coefficient, up to 10 when there is no competing reaction and even higher when another local reaction competes. How often this occurs is not known. An example is the positioning of hepatic glucose-6-phosphatase inside vesicles of endoplasmic reticulum (ER): the substrate G-6-P, and the products glucose and inorganic phosphate, traverse the ER membrane via specialized transporters, allowing access. The effect is seen also when enzymes inside endothelial cells compete for substrate, as adenosine kinase and adenosine deaminase compete for adenosine entering the cell. For transporters and any membrane-bound enzyme, the membrane phase (gel versus liquid) and fluidity may be important determinants of binding and fluxes (Finkelstein & Ghosh 1985).

The effect of steepening the flux–concentration relationships is to approach switch-like kinetics within metabolic networks. Such behaviour is also becoming evident in systems controlling gene expression. The existence of delays in feedback loops and sharply demarcated or steep response curves both contribute to instability in metabolic systems. Though Glass & Malta (1990) came to the conclusion that metabolic systems should not become chaotic, there is some evidence that period doubling oscillations and even chaotic behaviour can occur (Ghosh & Chance 1964; Chance et al. 1964a, b; Pye & Chance 1966). A good example is the glucose–insulin–ATP system studied by Markus & Hess (1985). Thus one needs to write the equations for individual reactions describing them as close to nature as is possible.

One of the hopes of metabolic control systems approaches to networks of reactions was to avoid having to characterize all of the little reactions. This hope has not been abandoned. But it is no longer so important to simplify computation to gain speed. Further, the greater availability of information means that reactions can be explicitly described, providing an understanding of mechanism, of activation processes, the formation of intermediates and the use of alternative pathways. The idea that in all species a given substrate goes through a specific reaction sequence to a specific product is incorrect. As genomes for more species come on line, it is often observed that in one species a reaction sequence has the same beginning and ending reactions as in a previously characterized species, but some of the expected proteins cannot be found. A search may then reveal either an alternative pathway or a protein that is quite different though it serves the same enzymatic function.

(k) The balancing acts

By developing the mathematical descriptions of the networks of reactions, filling in the gaps where needed by doing more experimental work, and using the models to design the experiments that test the hypotheses defined, quantitatively, by the models, one can do science—namely, figure out what is going on. A large set of balancing acts serves as a constraint on the modelling and on the parameter values themselves. These are first and foremost extensions of mass balance, what goes in goes out, in the steady state.

Mass balance must hold for carbon, hydrogen, nitrogen (ignored so far in the hypothetical cell that loses no protein), and oxygen. The buffering of pH by proteins and of cations by bicarbonate and other anions is also important. The balance is needed for purine nucleotides and nucleosides, for phosphate, sulphur and sulphate, and other ingredients. The sources and sinks of ATP are probably the greatest single set of influences on cell state.

Energy balance, phosphorylation and redox potentials follow from these. The ATP, GTP, NAD, and NADP levels all contribute directly to the governance of the fluxes through the networks. An individual reaction is not governed by the total cellular free energy, but by the difference in energy potential occurring with the reaction, and by the concentration of a particular supplier of energy for the reaction.

The same applies to oxidizing and reducing reactions. The cellular reduction–oxidation potential (redox state) depends on the reactions of reducing compounds, notably thiols, and is summarized by the NAD/NADH ratio.

The osmotic balance shifts in accord with the numbers of solute and solvent molecules inside cells. Metabolic breakdown of larger solutes such as glucose to smaller solutes, pyruvate and lactate, raises intracellular osmolarity so that there is a concentration gradient for water across the membrane: the cell swells. Ions are buffered by intracellular proteins, reducing their osmotic activities. The cell water content, and tissue water content, is remarkably constant in a given tissue. For example, the water content of the left ventricular myocardium is 0.78 ± 0.01 ml g⁻¹ (Yipintsoi et al. 1972); as expected, the specific gravity is normally also constant, ca. 1.06 g ml⁻¹, even though the variation in local flows per gram of tissue covers an eightfold range. Translated to the level of cell behaviour, these observations imply that even while cells within an organ may differ widely in their metabolic rates, there is remarkable ‘robustness’ and stability due to these balances. Homeostasis, in accord with Claude Bernard’s idea of a stable ‘milieu intérieure’ is provided by this robustness. Given the dynamic nature of cellular systems we do not expect exact homeostasis, but rather, because of external influences and internal dynamics, a homeodynamic, modestly fluctuating system.

The key to homeodynamic balance is control. There are no set points, reference points or levels to which the system is supposed to be matched. Control in some situations is very simple. One mechanism is that the controllers (of flow or oxygen delivery, for example) of the supply system are driven to change to match the demand (for tissue oxygen consumption). Others are much more complex, involving neural signalling pathways or intracellular signalling (see, for example, Shapiro et al. 2001).

4. Conclusion

The ‘simple sustainable’ cell model is designed as a building block, a primitive element upon which one can build more complete functional cell models of various types, representing various species. In the model outlined above we have perhaps overrepresented the electrophysiological aspects; the reason for this is that membrane potentials and their fluctuations have been generally omitted from metabolically oriented cell models in the past. Fluctuations in membrane potential deserve heightened consideration because probably all cells have negative intracellular potentials and most cells demonstrate electrical activity with vesicular extrusion, receptor occupancy, as well as with stimulated excitation.

The main points are the emphasis on the balances of mass, charge, and of chemical species while accounting for substrate uptake, metabolism and metabolite loss from the cell. By starting with a primitive representation we emphasize the conservation ideas. As more advanced models are generated they must adhere to the same basic principles as are required for the most primitive incomplete model.