An innovative Bayesian hierarchical modeling approach was used to combine longitudinal information from functional and structural tests for detection of glaucomatous progression. The methodology performed significantly better for detection of change over time than did the isolated use of structural or functional tests and the conventional approach of ordinary least-squares linear regression.
Abstract
Purpose.
To present and evaluate a new methodology for combining longitudinal information from structural and functional tests to improve detection of glaucoma progression and estimation of rates of change.
Methods.
This observational cohort study included 434 eyes of 257 participants observed for an average of 4.2 ± 1.1 years and recruited from the Diagnostic Innovations in Glaucoma Study (DIGS). The subjects were examined annually with standard automated perimetry, optic disc stereophotographs, and scanning laser polarimetry with enhanced corneal compensation. Rates of change over time were measured using the visual field index (VFI) and average retinal nerve fiber layer thickness (TSNIT average). A Bayesian hierarchical model was built to integrate information from the longitudinal measures and classify individual eyes as progressing or not. Estimates of sensitivity and specificity of the Bayesian method were compared with those obtained by the conventional approach of ordinary least-squares (OLS) regression.
Results.
The Bayesian method identified a significantly higher proportion of the 405 glaucomatous and suspect eyes as having progressed when compared with the OLS method (22.7% vs. 12.8%; P < 0.001), while having the same specificity of 100% in 29 healthy eyes. In addition, the Bayesian method identified a significantly higher proportion of eyes with progression by optic disc stereophotographs compared with the OLS method (74% vs. 37%; P = 0.001).
Conclusions.
A Bayesian hierarchical modeling approach for combining functional and structural tests performed significantly better than the OLS method for detection of glaucoma progression. (ClinicalTrials.gov number, NCT00221897.)
Detection of progression plays a central role in the diagnosis and management of glaucoma and standard automated perimetry (SAP) remains the method of choice for monitoring functional changes in the disease. However, there is evidence that many patients can present structural changes in the optic nerve or retinal nerve fiber layer (RNFL) before detectable changes in SAP.1–9 On the other hand, several patients show evidence of functional deterioration without measurable changes in currently available structural tests.4,5,10 The disagreement between structural and functional methods for detecting progression could be related to the different algorithms used to assess change, the variability of measurements over time, or the different scales used to assess structure and function.8,10–19 Whatever the reason might be, it is likely that a combination of structural and functional measurements would improve detection of clinically significant disease progression compared with either method used alone.
An ideal method for detection of glaucomatous progression should give not only an indication of whether the eye or the patient is showing progression, but also an estimate of the rate of deterioration. Although most glaucoma patients show some evidence of progression if followed up long enough, the rate of deterioration can be highly variable among them.9,20–23 Although most patients progress relatively slowly, others have aggressive disease with fast deterioration that can eventually result in blindness or substantial impairment unless appropriate interventions are made. The elucidation of the longitudinal relationship between structural and functional tests and their rates of change over time is essential to determine the relative utility of these tests in monitoring the disease.
In the present study, we propose a new methodology for combining longitudinal information from structural and functional tests to improve detection of glaucoma progression and estimation of rates of change. This approach is based on joint modeling of longitudinal changes using Bayesian hierarchical models. The joint modeling approach enables a better characterization of the true underlying relationship between structural and functional tests, as it decreases the impact of measurement error by incorporating it in a simultaneous model of the two longitudinal outcomes. By joint modeling of the two outcomes, information derived from one test is allowed to influence the inferences obtained from the other. For example, a visual field change that would otherwise be declared nonstatistically significant by analysis of visual field data alone may be declared significant after taking into consideration the structural changes occurring in the same eye. We applied our methodology to an investigation of longitudinal changes in SAP and RNFL thickness in a cohort of glaucoma patients and individuals suspected of having the disease followed over time.
Methods
This was an observational cohort study. Participants from this study were included in a prospective longitudinal study designed to evaluate optic nerve structure and visual function in glaucoma (DIGS; Diagnostic Innovations in Glaucoma Study) conducted at the Hamilton Glaucoma Center, University of California, San Diego. Participants in the DIGS were longitudinally evaluated according to a pre-established protocol that included regular follow-up visits in which patients underwent clinical examination and several other imaging and functional tests. All the data were entered in a computer database. All participants from the DIGS study who met the inclusion criteria described below were enrolled in the present study. The whole period of observation for the present study was from March 2002 to October 2010, but patients were enrolled at different times and had different durations of follow-up. Informed consent was obtained from all participants. The University of California San Diego Human Subjects Committee approved all protocols, and the methods described complied with the tenets of the Declaration of Helsinki.
At each visit during follow-up, subjects underwent a comprehensive ophthalmic examination, including review of medical history, best corrected visual acuity, slit lamp biomicroscopy, intraocular pressure (IOP) measurement, gonioscopy, dilated funduscopic examination, stereoscopic optic disc photography, and automated perimetry (SITA Standard 24-2). Only subjects with open angles on gonioscopy were included. The subjects were excluded if they presented best corrected visual acuity less than 20/40, spherical refraction outside ± 5.0 D. and/or cylinder correction outside 3.0 D or any other ocular or systemic disease that could affect the optic nerve or the visual field.
The study included patients with diagnosed glaucoma as well as those with suspected disease, as determined on the baseline visit. Eyes were classified as glaucomatous if they had repeatable (two consecutive) abnormal visual field test results on the baseline visits, defined as a pattern standard deviation (PSD) outside the 95% normal confidence limits, or a Glaucoma Hemifield Test result outside normal limits. Eyes were classified as having suspected glaucoma if they had a history of elevated intraocular pressure (>21 mm Hg) and/or glaucomatous or suspicious appearance of the optic nerve but normal and reliable visual field results on the baseline visits.
The study also included a cohort of healthy subjects recruited from the general population and from hospital staff. These subjects had normal-appearing optic discs and no evidence of progressive optic disc damage over time, by masked optic disc stereophotograph assessment. They also had normal visual fields at the baseline visit and no history of elevated IOP. This cohort was used to assess the specificity of our proposed methodology.
Standard Automated Perimetry
Only reliable tests (≤33% fixation losses and false negatives and <15% false positives) were included. Evaluation of rates of visual field change during follow-up was performed using the visual field index (VFI; Humphrey perimeter; Carl-Zeiss Meditec, Inc., Dublin, CA). Details of the calculation of the VFI have been described elsewhere.24 In brief, the VFI represents the percent of normal age-corrected visual function, and it is intended for use in calculating rates of progression and staging glaucomatous functional damage. Evaluation of rates of functional loss in glaucomatous eyes with the VFI has been proposed to be less susceptible than the mean deviation (MD) to the effects of cataract or diffuse media opacities.24–26 The VFI can range from 100% (normal visual field) to 0% (perimetrically blind field). The current Humphrey software analyzes the rate of VFI change over time using ordinary least-squares (OLS) linear regression, and the printout shows a message indicating whether the slope of the regression line is statistically significant.
Stereophotograph Grading
Simultaneous stereoscopic optic disc photographs (TRC-SS; Topcon Instrument Corp. of America, Paramus, NJ) were reviewed with a stereoscopic viewer (Asahi Pentax Stereo Viewer II; Asahi Optical Co., Tokyo, Japan). For progression assessment, each patient's most recent stereophotograph was compared with the baseline one. Definition of change was based on focal or diffuse thinning of the neuroretinal rim and increased excavation, appearance, or enlargement of RNFL defects. Evidence of progression was based on masked (patient name, diagnosis, temporal order of photographs) comparison between the baseline and most recent photograph, by two observers. If these observers disagreed, a third observer served as an adjudicator.
Scanning Laser Polarimetry
Patients were imaged using a commercially available scanning laser polarimeter (SLP) with enhanced corneal compensation (GDx ECC; Carl-Zeiss Meditec). The general principles of scanning laser polarimetry and the algorithms used for enhanced corneal compensation have been described in detail elsewhere.27–30 Assessment of SLP image quality was performed by an experienced examiner masked to the subject's identity and the results of the other tests. To be classified as good quality, an image required a focused and evenly illuminated reflectance image with a centered optic disc. The image quality score had to be greater than or equal to 7. Image quality was evaluated by masked trained technicians at a reading center.31
RNFL retardation measurements were obtained on a 3.2-mm diameter calculation circle around the optic nerve head. For this study, we used the TSNIT average parameter, which represents the global average RNFL thickness (calculated as the average of the RNFL measurements obtained on the 360° around the optic nerve) and is provided on the standard GDx printout. The GDx provides measurements of RNFL retardation, which are converted to estimated RNFL thickness using a fixed conversion factor.
Average follow-up time was 4.2 ± 1.1 years. A minimum of three SLP examinations and three SAP tests were required during follow-up. The study included a total of 1651 SLP visits. The number of visits per eye ranged from three to seven, with 61% of the eyes having at least four visits during follow-up. A total of 2493 visual field test results were available during the corresponding follow-up period. The number of visual field tests per eye ranged from 3 to 12, with 75% of the eyes having at least five tests during follow-up. During the follow-up, each patient was treated at the discretion of the attending ophthalmologist.
Bayesian Hierarchical Modeling Approach
A joint multivariate mixed-effects model was implemented within a Bayesian hierarchical modeling framework to evaluate the relationship between the two longitudinal measures obtained over time (i.e., the GDx RNFL measurements and SAP VFI).32–35 Linear mixed models were used to evaluate the evolution of each response over time. In these models, the average evolution of a specific response is described using some function of time, and subject-specific deviations from this average evolution are introduced by random intercepts and random slopes, allowing for different baseline values and different rates of change for each patient. Linear mixed models are a natural extension of Bayesian hierarchical models, where the first level of hierarchy corresponds to within-patient variation and the second level to between-patient variation. The Bayesian framework, however, allows more flexible specification of the model assumptions and easier implementation of the joint modeling approach, as described below.36–42
In a joint modeling approach using mixed models, random-effects are assumed for each response process and the different processes are associated by imposing a joint multivariate distribution on the random effects. This approach has great flexibility and allows the joining of models for responses of different types and also with a different number of observations, as in our application.32
Each response process is described using the following linear mixed-effects model
where Y1 and Y2 represent the longitudinal measurements of SLP and SAP, respectively, for a subject i taken at time t, and m1(t) and m2(t) represent the average linear evolution of each response over time, that is, the average rate of change of SLP measurements and the average rate of change in SAP sensitivity. Both response trajectories are tied together through a multivariate distribution of the random effects, where a1 and b1 correspond to random intercepts and random slopes, respectively, for process 1 (SLP), and a2 and b2 correspond to random intercepts and random slopes for process 2 (SAP). By adding an additional level for eye nested within patient, it is also possible to use information from both eyes of the same patient taking into account the correlation between them.
Conventional linear mixed models assume a normal distribution of random effects. However, previous studies have shown that the general assumption of normally distributed random effects may lead to biased estimates of individual change parameters when there is heterogeneity in the population.43,44 In the present application, heterogeneity is to be expected, as only a proportion of eyes will show progression over time. Further, in the progressing group, only a small proportion is expected to have relatively fast progression. This situation can induce considerable nonnormality, or skewness, in the random effects distribution. To address the problem, we used a multivariate skew t distribution to model random effects. Both the t and skew t distributions allow greater flexibility in the distribution of random effects compared with the normal distribution and have been successfully applied to model nonnormal random effects.41,45 The probability density function for a random effect bj that is t distributed t(μ, v, k) is
where μ is the mean, v the scale parameter, and k the degrees of freedom determining the weight of the tails, giving variance σ2 = [k/(k − 2)]v. The t distribution can be extended to accommodate the multivariate case.46 To allow for skewing, Fernandez and Steel47 proposed the introduction of skewness to any unimodal distribution symmetric ∼0, using a scale factor γ on each side of 0. For a random variable −∞ < x < ∞, this method gives:
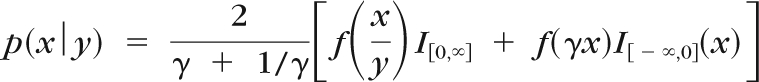 |
where I[c,d] is the indicator function for x, being between c and d, and γ controls the mass on each side of 0, representing the skewness.
Therefore, in our Bayesian model, the intercepts and slopes were assumed to follow a multivariate skew t distribution. This multivariate distribution acted as a “prior” for the estimation of the intercepts and slopes for each eye and the parameters of the multivariate distribution were themselves estimated from the data. However, to perform Bayesian inference, we also need to specify priors for the parameters of the multivariate distribution (i.e., the hyperparameters). Unless there are strong prior beliefs in the hyperparameter values, it is usually desirable to use noninformative priors. Therefore, we used normal (0,1000) for μ and uniform (0,100) for σ.48 An exponential (0.1) prior was used for k in the t distribution,47 but restricted to k > 2.5 to prevent problems with undefined variance when k ≤ 2. For the skew parameter γ, we used a γ(0.5, 0.318) prior for φ = γ2. These are general priors used in previous applications of Bayesian hierarchical models using t and skew t distributions.45
Estimates of the posterior distributions of the parameters of interest (i.e., the random effects, were obtained by Markov chain Monte Carlo (MCMC) procedures. The MCMC sampler was implemented in WinBUGS software.49 We used 10,000 iterations after discarding the initial 5,000 iterations for burn-in. Convergence of the generated samples was assessed by standard tools in WinBUGS (trace plots and autocorrelation function [ACF] plots) as well as Gelman-Rubin convergence diagnostics. After the posterior distributions were estimated, summary measures were calculated, such as mean and credible intervals. For a specific test, we considered that progression had occurred if the upper limit of the 95% credible interval for the slope was less than 0.
Importantly, no information on the classification of subjects (i.e., whether there was optic disc progression on stereophotographs or not) was inserted into the model. Also, the likelihood information from healthy eyes was not allowed to influence calculations of model parameters. This was done to have a model that would reflect a population that is commonly followed under a clinical scenario, that is, composed of eyes with glaucoma or suspected of having disease. We calculated sensitivity, specificity, and receiver operating characteristic (ROC) curves as measures of discrimination. To estimate the effect of the sample composition on the predictive distribution, we ran 200 bootstrap resamples and re-estimated sensitivity and specificity. To avoid potential biases in the estimation of sensitivity and specificity, we also used a leave-one-out approach to calculate the estimates for individual eyes. That is, the model was built with information from n − 1 eyes and applied to obtain the estimates of progression in the nth eye. We compared our algorithm for detection of progression to standard approaches reported on the printouts of the instruments and used in previous studies.8,10,25,50–53 The standard approach is based on OLS linear regression of measurements over time, so that an eye is considered to have progressed if a negative OLS regression slope is significantly different from 0, with P < 0.05. OLS regressions were performed separately for each eye and for each test (i.e., SAP VFI and SLP TSNIT average).
Results
The study included 434 eyes of 257 participants with a mean ± SD age of 63 ± 12 years at baseline. One hundred fifty-four (60%) patients were women. Of the 434 eyes included in the study, 165 (38%) had glaucomatous visual field loss at the baseline visit, 240 (55%) were classified as suspect, and 29 (7%) were healthy eyes. Median (first quartile, third quartile) MD and PSD of the visual field closest to the baseline imaging test date in glaucomatous eyes were −2.93 dB (−5.40 to −1.62) and 3.00 dB (2.34–5.25), respectively. Corresponding values for glaucoma suspect eyes were −0.60 dB (−1.42 to 0.19) and 1.51 dB (1.33–1.69), respectively, and for healthy eyes were −0.46 dB (−1.14 to 0.26) and 1.48 dB (1.33–1.78), respectively. There was a large variation in baseline MD in the eyes included in the study, with values ranging from −21.9 to 1.9 dB.
Bayesian Slopes of Change
Of the 405 glaucomatous and suspect eyes, 92 (22.7%) had progression according to Bayesian slopes of change for VFI and/or TSNIT average. Of these 92 eyes, 26 (28%) progressed by both tests, 5 (5%) progressed by visual fields only, and 61 (66%) progressed by SLP only. Figure 1 shows Venn diagrams representing the number of eyes progressing by the Bayesian method in structure, function, or both, according to their baseline classification. Bayesian slopes of change for VFI in progressing eyes were significantly faster than those of nonprogressing eyes (−0.81% ± 1.17 per year vs. −0.03% ± 0.14% per year). Similarly, Bayesian slopes of change for TSNIT average for progressing eyes were significantly faster than those of nonprogressing eyes (−1.15 ± 0.72 μm/year vs. −0.28 ± 0.28 μm/y).
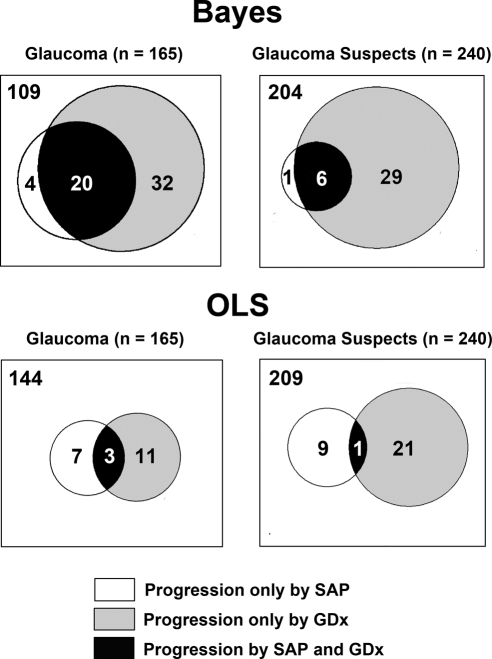
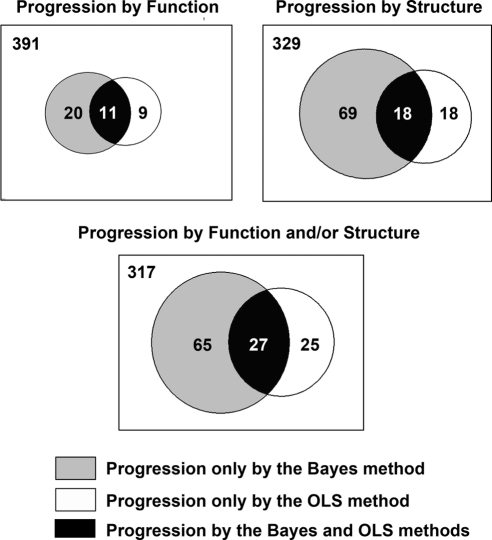
Figure 1.
Proportional Venn diagrams illustrating the number of eyes identified as progressing by the Bayesian and OLS methods, according to the baseline diagnosis. The areas of the circles are proportional to the number of subjects in each category.
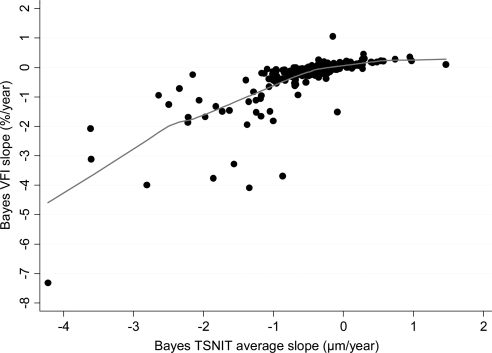
Figure 2 shows the relationship between Bayesian slopes of change calculated for VFI and TSNIT average. There was a significant relationship between slopes of change for VFI and TSNIT average (Spearman's ρ = 0.81; P < 0.001). However, eyes that progressed only by TSNIT average tended to have less severe baseline disease than did those that progressed by both methods, as indicated by differences in average baseline values for VFI (94% ± 11% vs. 87% ± 12%; P = 0.004), respectively.
Figure 2.
Relationship between slopes of change in the VFI and TSNIT average parameter over time obtained by the Bayesian method. A locally weighted scatterplot smoothing (LOWESS) was fit to the plot.
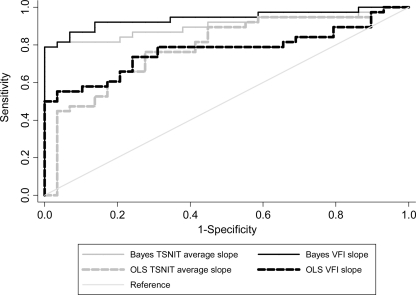
Of the 29 healthy eyes, none was identified as progressing by Bayesian slopes of change for VFI or TSNIT average, resulting in a specificity of 100% (95% CI, 88%–100%) for the combined method. Of the 405 glaucomatous and suspect eyes, 38 eyes had evidence of progressive glaucomatous optic neuropathy (PGON) on optic disc stereophotographs. The Bayesian method detected 28 of these eyes, resulting in a sensitivity of 74% (95% CI, 57%–87%) for this group. Table 1 shows average slopes of change according to the Bayesian method for healthy and PGON groups. The areas under the ROC curves to discriminate healthy eyes from those with progressive optic disc damage on stereophotographs were 0.94 ± 0.03 and 0.90 ± 0.04 for Bayesian slopes of change for VFI and TSNIT average, respectively (Fig. 3). The bias-corrected estimates of sensitivity and specificity were 72% and 99%, respectively.
Table 1.
Slopes of Change over Time and Areas under the ROC Curves to Discriminate Eyes That Had PGON on Optic Disc Stereophotographs from Healthy Eyes
| PGON (n = 38) | Healthy (n = 29) | P† | AUC (SE) | |
|---|---|---|---|---|
| Bayesian VFI slope, %/y | −0.82 ± 1.34 | 0.01 ± 0.08 | <0.001 | 0.94 (0.03) |
| Bayesian TSNIT slope, μm/y | −1.04 ± 0.80 | −0.24 ± 0.20 | <0.001 | 0.90 (0.04) |
| OLS VFI slope, %/y | −1.11 ± 1.67 | 0.10 ± 0.48 | <0.001 | 0.77 (0.06) |
| OLS TSNIT slope, μm/y | −1.27 ± 1.46 | 0.47 ± 1.74 | <0.001 | 0.81 (0.05) |
Data are the mean ± SD.
*Bayesian slope indicates slopes obtained through the Bayesian hierarchical regression model.
Mann-Whitney U test.
Figure 3.
ROC curves to discriminate eyes that showed progression on optic disc stereophotographs versus healthy eyes for the Bayesian and OLS methods.
OLS Slopes of Change
We also evaluated the ability of OLS linear regression in detecting change. Of the 405 glaucomatous and suspect eyes, 52 (12.8%) were identified as progressing by OLS slopes of change for VFI and/or TSNIT average. Of these 52 eyes, only 4 (7.7%) had progression by both tests, whereas 16 (31%) had progression only by VFI and 32 (61.5%) had progression only by SLP. Figure 1 also shows Venn diagrams representing the number of eyes progressing by the OLS method in structure, function, or both, according to their baseline classification. OLS slopes of change for VFI in progressing eyes were significantly faster than those of nonprogressing eyes (−0.75% ± 1.26% per year vs. −0.11% ± 0.96% per year). OLS slopes of change for TSNIT average for progressing eyes were also significantly faster than those of nonprogressing eyes (−1.37 ± 1.19 μm/year vs. −0.33 ± 1.04 μm/year).
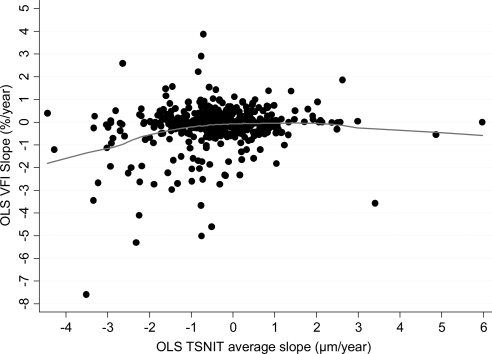
Figure 4 shows the relationship between OLS slopes of change calculated for VFI and TSNIT average. There was only a very weak, albeit statistically significant, relationship between OLS slopes of change for VFI and TSNIT average (Spearman's ρ = 0.10; P = 0.04).
Figure 4.
Relationship between slopes of change in the VFI and TSNIT average parameter over time obtained by the OLS linear regression method. A locally weighted scatterplot smoothing (LOWESS) was fit to the plot.
Of the 29 healthy eyes, none was identified as progressing by OLS slope of change for VFI or TSNIT average, resulting in a specificity of 100% (95% CI, 88%–100%). Of the 38 glaucomatous and suspect eyes that had evidence of progressive GON by optic disc stereophotographs, the OLS method was able to detect only 14, resulting in a sensitivity of only 37% (95% CI, 22%–54%) for this group. Table 1 also shows average slopes of change in the healthy and PGON groups, according to the OLS method. The areas under the ROC curve to discriminate healthy eyes from those with progressive optic disc damage on stereophotographs were 0.77 ± 0.06 and 0.79 ± 0.06 for OLS slopes of change for VFI and TSNIT average, respectively (Fig. 3).
Comparison between Bayesian and OLS Slopes of Change
The Bayesian method identified a significantly higher proportion of glaucomatous and suspect eyes as having progressed compared with the OLS method (22.7% vs. 13%; P < 0.001), while showing the same specificity in healthy eyes. In addition, the Bayesian method identified as progressing a significantly higher proportion of eyes that had progression on optic disc stereophotographs compared to the OLS method (74% vs. 37%; P = 0.001). The ROC curve areas to discriminate healthy eyes from those with PGON on stereophotographs were significantly larger for the Bayesian method compared with OLS regression for VFI slopes (0.94 vs. 0.77; P < 0.001) and for TSNIT average slopes (0.90 vs. 0.79; P = 0.004), respectively.
We also examined the factors related to the differences between detection of progression by the Bayesian and OLS methods. Figure 5 shows Venn diagrams representing the agreement between the two methods for detection of progression. Sixty-five eyes were detected as progressing only by the combined Bayesian method, whereas 25 eyes were detected as progressing only by the OLS method (VFI and/or TSNIT). Table 2 shows average slopes of change for the Bayesian and OLS methods, along with average SE of the slopes of change, which indicate the variability of measurements over time and precision in the estimation of the slopes. In general, eyes progressing only by the Bayesian method had faster rates of change than those progressing only by OLS, but the large standard errors of the slopes precluded their identification by the OLS method. The presence of concomitant structural change in these eyes allowed the combined Bayesian method to declare the functional changes as significant and vice versa. Eyes progressing only by the OLS method had relatively slower and clinically insignificant rates of visual field loss that were not supported by concomitant changes in structure (and vice versa) and, therefore, were declared as nonprogressors by the Bayesian method.
Figure 5.
Proportional Venn diagrams illustrating the agreement between the Bayesian and OLS methods in detecting structural (TSNIT average) and functional (standard automated perimetry visual field index [VFI]) change over time. The areas of the circles are proportional to the number of subjects in each category.
Table 2.
Differences in Slopes of Change and Standard Errors of the Slopes between Eyes that Progressed According to the Two Linear Regression Methods
| Progression Only by the Bayesian Method (n = 65) | Progression Only by the OLS Method (n = 25) | P† | |
|---|---|---|---|
| VFI | |||
| Average Bayesian slope | −0.74 ± 1.23 | −0.08 ± 0.11 | <0.001 |
| Average standard error of the Bayesian slopes | 0.46 ± 0.26 | 0.31 ± 0.04 | <0.001 |
| Average OLS slope | −0.90 ± 1.55 | −0.11 ± 0.39 | <0.001 |
| Average standard error of the OLS slopes | 1.06 ± 1.20 | 0.34 ± 0.30 | <0.001 |
| TSNIT Average | |||
| Average Bayesian slope | −1.04 ± 0.62 | −0.40 ± 0.32 | <0.001 |
| Average standard error of the Bayesian slopes | 0.58 ± 0.24 | 0.42 ± 0.11 | <0.001 |
| Average OLS slope | −1.44 ± 0.98 | −0.99 ± 0.84 | 0.033 |
| Average standard error of the OLS slopes | 0.84 ± 0.75 | 0.28 ± 0.38 | <0.001 |
*Progression only by Bayesian indicates eyes that progressed according to the combined Bayesian method (structure and/or function). Progression only by OLS indicates eyes that progressed only by the OLS linear regression method (structure and/or function).
Mann-Whitney U test.
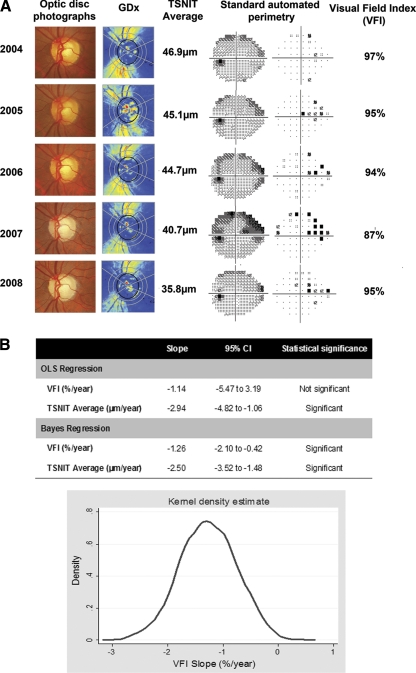
Figure 6 illustrates a case of detection of glaucoma progression with the combined Bayesian method.
Figure 6.
(A) SAP and SLP results in an eye that had progressive glaucomatous optic neuropathy over time on optic disc stereophotographs. There was progressive RNFL thinning, as shown by the color-coded map and a decrease in TSNIT average values over time. SAP shows progressive visual field defect on the superior nasal sector. (B) Slopes of change for VFI and TSNIT average obtained by OLS regression and the combined Bayesian method for the examinations shown in (A). The OLS regression slope for VFI was not statistically significant, whereas the Bayesian VFI slope was significantly less than 0. The Bayesian slope for the functional test (VFI) was influenced by the presence of significant changes in the structural test (TSNIT average). The graph shows the kernel density estimate for the posterior distribution of the slope of VFI change obtained by the Bayesian hierarchical model.
Discussion
In the present study, we proposed an innovative methodology for the combination of structural and functional tests for detection of longitudinal change in glaucoma. Our approach identified a significantly larger proportion of eyes with glaucoma and suspected disease as having progressed over time compared with the conventional method of OLS linear regression that is commonly used by the software of commercially available instruments. To our knowledge, this is the first study to report a successful method of combining longitudinal structural and functional tests in glaucoma using Bayesian methodology.
The use of a combined approach for evaluation of structural and functional change provides several advantages compared with an analysis of change in structure or function performed separately. The joint model allows for the correlation between structural and functional change over time and, therefore, inferences on the significance of functional change are influenced by the presence of structural change and vice versa. This is likely to explain the improved detection of glaucoma progression with the combined Bayesian approach, as shown in our study. In fact, of the 405 eyes with diagnosed or suspected glaucoma, the combined Bayesian approach identified 92 (22.7%) eyes as progressing compared with only 52 (12.8%) for the OLS regression method. In addition, we tested the performance of the method in identifying a group of eyes classified as progressing based on optic disc stereophotographs. The presence of progression on optic disc stereophotographs has been shown to be highly predictive of the risk of future visual field loss1 and, therefore, is a suitable, although still imperfect, reference method for detection of progression.54 In the subjects with PGON by optic disc photos, the Bayesian method also largely outperformed the OLS regression approach with sensitivity of 74% compared to 37%, respectively.
Because there is no perfect independent reference standard to detect progression, it is difficult to estimate the sensitivity and specificity of our combined Bayesian method for detection of change. Although we have compared our method to detection of optic disc change by stereophotographs, it is known that many cases of progression can be missed if optic disc stereophotographs are used as the sole method of detecting change, especially in more advanced cases of disease.4,5 That is, optic disc photos have limited sensitivity. Therefore, if we rely on optic disc stereophotographs as the only reference standard, many eyes with true progression will not be detected, which is likely to make the test under investigation appear to have a high number of false positives. If we had estimated specificity on the basis of the number of the 405 glaucomatous and suspect eyes that had no change on optic disc stereophotographs, the specificities would be 82.6% and 89.6% for the combined Bayesian and OLS methods, respectively. It is likely that these specificities would be underestimated because of the inability of optic disc stereophotographs to detect all cases of glaucoma progression. In fact, the very high specificity of the combined Bayesian method when applied to healthy eyes suggests that the significant changes detected in the glaucoma and suspect population were indeed representative of true disease deterioration. It should be noted, however, that estimation of specificities in a group of healthy eyes is not without problems. In clinical practice, visual fields and imaging instruments are applied to detect and monitor disease in diseased eyes or those with suspected glaucoma. Healthy eyes may have different characteristics from the eyes followed in clinical practice such as visual field variability, for example, and therefore estimates of specificity obtained from healthy eyes may be different from those in the clinically relevant population. For this reason, some authors8 have used as a surrogate for specificity the proportion of eyes showing positive slopes on the clinical tests, based on the assumption that real improvement does not occur in glaucoma. Using this approach, the Bayesian and OLS methods would have specificities of 100% and 97.7%, respectively, in the 405 eyes of with diagnosed and suspected glaucoma.
Clinicians frequently try to integrate results from structural and functional testing to detect disease progression. This is done routinely, as they attempt to correlate changes in their examinations of the optic nerve to those occurring in the visual field, so that if changes over time are seen in both methods, they are more reassuring to indicate true deterioration. However, clinicians are frequently uncertain about how to interpret apparently conflicting results coming from different tests. Also, the use of many different tests can increase the chance of a type I error (i.e., declaring as significant a change that actually has occurred by chance). The approach of joint modeling of structural and functional testing largely overcomes these limitations. By using joint models, it is possible to keep the chance of type I error under control.55 In addition, the correlation between results of both methods is formally taken into account in the model decision framework, which helps solve potentially conflicting results. Using the combined Bayesian method, a visual field change that would otherwise be declared nonstatistically significant by analysis of visual field data alone was declared significant after taking into consideration the structural changes occurring in the same eye and vice versa. In fact, many eyes with relatively fast rates of visual field loss were declared as nonprogressing by the OLS method in our study due to the variability of measurements over time (i.e., large SE of the OLS regression slope), as shown in Table 2 and Figure 6. In these cases, one frequently has to obtain more tests to attempt to more precisely estimate the slope of OLS regression. However, in clinical practice, there is a cost associated with obtaining more measurements over time, including the expense of the test itself, the cost in patient time, and the cost related to delaying detection of change. The current Humphrey Field Analyzer printout requires a minimum of five visual field tests to calculate the OLS slope. Therefore, we reanalyzed our results on eyes with a minimum of five visual fields. From the group of eyes with progressive optic disc damage, 27 eyes had at least five visual fields. The Bayesian approach was able to detect 22 (81%) of these eyes versus only 11 (41%) of the OLS approach. Therefore, there was a benefit of the Bayesian approach, even when only eyes with a greater number of tests were considered. Although different techniques have been used in an attempt to decrease the impact of variability in the detection of visual field progression, to our knowledge, no previous method has been reported that combines structural and functional change.
The combined Bayesian approach resulted in much better agreement between structural and functional changes, with a Spearman's rank correlation of 0.81 compared with only 0.10 for the correlation between OLS slopes. Twenty-six eyes had progression in both structure and function with the Bayesian method, as opposed to only four eyes, using conventional OLS regression. The better agreement seen with the combined Bayesian method results from a better characterization of the true underlying relationship between the two tests, as it decreases the impact of measurement error by incorporating it in a joint model of the two longitudinal outcomes.32–35,56 It is important to note, however, that even with the combined Bayes method, some eyes were identified as progressing by structure or by function only. Such a level of disagreement is not surprising, and several previous studies have also documented disagreement on detection of glaucoma progression by different tests. The disagreement could be related to the ability of the tests in identifying progression at different stages of the disease. Previous studies have suggested that SLP may be better suited for detection of progression at relatively early stages of disease, whereas the technology may fail to detect change in cases with advanced damage.9,15,19,23,26,57 On the other hand, the logarithmic scaling of clinical perimetric data may favor detection of change in later stages of disease with SAP.2,58 Also, VFI values only show decrease after a certain threshold of abnormality on the pattern deviation plot has been exceeded.24 In fact, the eyes that progressed only by SLP in our study had significantly less severe baseline disease than did the eyes that progressed by visual fields. The presence of disagreement actually reinforces the need for a combined approach for detection of glaucoma progression to allow effective monitoring of the disease at all stages of damage. It is important to emphasize that, for the combined Bayes approach, the presence of clear change in function was still declared as significant, even when not occurring concomitantly to a change in structure, and vice versa. By joint modeling random intercepts and slopes for SLP and SAP, the Bayesian approach can also take into consideration the influence of different stages of disease severity on the slopes of change.
It is important to emphasize that no information about the classification of subjects was entered on the Bayesian model. Therefore, our methodology can be used to classify individual eyes as progressing or nonprogressing. Also, it provides estimates of rates of change over time. Although we applied our methodology to VFI and scanning laser polarimetry data, it is likely that it will also perform well in combining other methods of evaluation of functional and structural loss, such as other perimetric indexes combined with measurements from technologies such as OCT and confocal SLO. When we conducted similar analyses using the MD index in our study, we obtained similar results (not shown), which is not surprising, in that the correlation between VFI and MD values in our dataset was very high (r = 0.93).
Bayesian estimates of slopes of change, as obtained from hierarchical models, are considered shrinkage estimates, which depend not only on the actual data for the eye being evaluated, but also on data available from the overall population of eyes. This actually represents another potential advantage of the method compared to OLS regression, as we have shown in a previous study.59 Although rates of change in glaucoma have traditionally been estimated using OLS linear regression, the true rate of change, however, is actually a latent or unobservable variable, and the slope of change obtained from OLS is just an imprecise estimate that is confounded by noise and influenced by the number and intervals of measurements during follow-up. OLS estimates are obtained taking into account only the measurements of an individual patient, without considering the influence of the population where the patient comes from. The Bayesian hierarchical modeling approach, however, improves the precision of an individual patient's estimate of slope of change by using previously longitudinally collected data from other patients. For example, it is reasonable to assume that the best estimator of the rate of change in a patient in whom we do not have any measurements collected over time is the average rate of change in the overall population of which the individual is a part. As measurements are acquired for this patient, however, the rate of change will most likely deviate from the population average. For patients with fewer measurements, the precision of the estimates can be increased by “borrowing strength” from the population, whereas for patients with large number of measurements, precise estimates can be obtained relying almost only on the individual data and the need to borrow strength from the population decreases. It is also worth emphasizing that the combined structure–function approach, as reported in this study, is still advantageous compared with Bayesian slopes of change obtained by applying the Bayesian methodology to each test separately. For example, 23% of the eyes detected as progressing by the VFI using the combined approach would not be detected as progressing if structural information was not included in the model. Conversely, 18% of the eyes would not be detected by TSNIT slopes if the Bayesian model did not include functional information.
It is important to note that our approach requires an adequate and sufficiently large sample of patients similar to the patients in whom we want to make predictions. In our study, we used a large group of patients with diagnosed glaucoma and suspected glaucoma that have been longitudinally studied according to prespecified protocols for many years. In addition, using bootstrap resampling, we showed that the estimates were robust against variations in the composition of the sample. Construction of similar built-in databases would be necessary to implement this methodology in currently available instruments. Another potential advantage of our methodology is that data from patients tested over time could be continuously incorporated into the Bayesian model, leading to improved estimates that would more likely reflect the progression rates in a particular clinical setting, generating a “customized” database for comparison. The generalizability of our modeling approach will have to be tested under different clinical scenarios, including patients observed in other geographic areas, with different degrees of disease severity and under different clinical protocols.
Our study had limitations. We assumed a linear rate of structural and functional change over time. Findings in previous studies using cross-sectional data, however, suggest that functional changes over the whole course of the disease would probably not be linear.2,60–66 However, the assumption of linear change is probably a reasonable one when evaluating change in periods of short- to medium-term follow-up, as performed in clinical practice. It should be noted, however, that extensions of our methodology to incorporate nonlinear change are also possible, but the evaluation is likely to require populations with longer follow-up times.
In conclusion, a Bayesian hierarchical modeling approach for combining functional and structural tests performed significantly better than the conventional OLS method of detection of glaucoma progression. Combining structural and functional measurements is likely to improve our ability to effectively monitor the disease and estimate rates of deterioration.
Footnotes
Supported in part by an American Glaucoma Society research grant (FAM) and by the National Eye Institute Grants EY08208 (FAM) and EY11008 (LMZ). Participant retention incentive grants in the form of glaucoma medication at no cost: Alcon Laboratories Inc., Allergan, Pfizer Inc., and SANTEN Inc.
Disclosure: F.A. Medeiros, Carl-Zeiss Meditec, Inc. (F), Heidelberg Engineering (R); M.T. Leite, None; L.M. Zangwill, Heidelberg Engineering (F, R), Carl-Zeiss Meditec, Inc. (F); R.N. Weinreb, Carl-Zeiss Meditec, Inc. (F), Heidelberg Engineering (F)
References
- 1. Medeiros FA, Alencar LM, Zangwill LM, Bowd C, Sample PA, Weinreb RN. Prediction of functional loss in glaucoma from progressive optic disc damage. Arch Ophthalmol. 2009;127(10):1250–1256 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Hood DC, Kardon RH. A framework for comparing structural and functional measures of glaucomatous damage. Prog Retin Eye Res. 2007;26(6):688–710 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Harwerth RS, Carter-Dawson L, Smith EL, 3rd, Barnes G, Holt WF, Crawford ML. Neural losses correlated with visual losses in clinical perimetry. Invest Ophthalmol Vis Sci. 2004;45(9):3152–3160 [DOI] [PubMed] [Google Scholar]
- 4. Kass MA, Heuer DK, Higginbotham EJ, et al. The Ocular Hypertension Treatment Study: a randomized trial determines that topical ocular hypotensive medication delays or prevents the onset of primary open-angle glaucoma. Arch Ophthalmol. 2002;120(6):701–713, 2002; discussion 829–730 [DOI] [PubMed] [Google Scholar]
- 5. Miglior S, Zeyen T, Pfeiffer N, Cunha-Vaz J, Torri V, Adamsons I. Results of the European Glaucoma Prevention Study. Ophthalmology. 2005;112(3):366–375 [DOI] [PubMed] [Google Scholar]
- 6. Wollstein G, Schuman JS, Price LL, et al. Optical coherence tomography longitudinal evaluation of retinal nerve fiber layer thickness in glaucoma. Arch Ophthalmol. 2005;123(4):464–470 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Strouthidis NG, Scott A, Peter NM, Garway-Heath DF. Optic disc and visual field progression in ocular hypertensive subjects: detection rates, specificity, and agreement. Invest Ophthalmol Vis Sci. 2006;47(7):2904–2910 [DOI] [PubMed] [Google Scholar]
- 8. Leung CK, Cheung CY, Weinreb RN, et al. Evaluation of retinal nerve fiber layer progression in glaucoma: a study on optical coherence tomography guided progression analysis. Invest Ophthalmol Vis Sci. 2010;51(1):217–222 [DOI] [PubMed] [Google Scholar]
- 9. Medeiros FA, Alencar LM, Zangwill LM, Sample PA, Weinreb RN. The relationship between intraocular pressure and progressive retinal nerve fiber layer loss in glaucoma. Ophthalmology. 2009;116(6):1125–1133, e1121–1123 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Artes PH, Chauhan BC. Longitudinal changes in the visual field and optic disc in glaucoma. Prog Retin Eye Res. 2005;24(3):333–354 [DOI] [PubMed] [Google Scholar]
- 11. Chauhan BC, Hutchison DM, Artes PH, et al. Optic disc progression in glaucoma: comparison of confocal scanning laser tomography to optic disc photographs in a prospective study. Invest Ophthalmol Vis Sci. 2009;50(4):1682–1691 [DOI] [PubMed] [Google Scholar]
- 12. Vesti E, Johnson CA, Chauhan BC. Comparison of different methods for detecting glaucomatous visual field progression. Invest Ophthalmol Vis Sci. 2003;44(9):3873–3879 [DOI] [PubMed] [Google Scholar]
- 13. Chauhan BC, McCormick TA, Nicolela MT, LeBlanc RP. Optic disc and visual field changes in a prospective longitudinal study of patients with glaucoma: comparison of scanning laser tomography with conventional perimetry and optic disc photography. Arch Ophthalmol. 2001;119(10):1492–1499 [DOI] [PubMed] [Google Scholar]
- 14. Xin D, Greenstein VC, Ritch R, et al. A Comparison of functional and structural measures for identifying progression of glaucoma. Invest Ophthalmol Vis Sci. 2011;52:519–525 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Alencar LM, Zangwill LM, Weinreb RN, et al. Agreement for detecting glaucoma progression with the GDx guided progression analysis, automated perimetry, and optic disc photography. Ophthalmology. 2010;117(3):462–470 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Medeiros FA, Zangwill LM, Alencar LM, et al. Detection of glaucoma progression with stratus OCT retinal nerve fiber layer, optic nerve head, and macular thickness measurements. Invest Ophthalmol Vis Sci. 2009;50(12):5741–5748 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Strouthidis NG, White ET, Owen VM, Ho TA, Hammond CJ, Garway-Heath DF. Factors affecting the test-retest variability of Heidelberg retina tomograph and Heidelberg retina tomograph II measurements. Br J Ophthalmol. 2005;89(11):1427–1432 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Medeiros FA, Alencar LM, Zangwill LM, Sample PA, Susanna R, Jr, Weinreb RN. Impact of atypical retardation patterns on detection of glaucoma progression using the GDx with variable corneal compensation. Am J Ophthalmol. 2009;148(1):155–163, e151 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Grewal DS, Sehi M, Greenfield DS. Detecting glaucomatous progression using GDx with variable and enhanced corneal compensation using Guided Progression Analysis. Br J Ophthalmol. 2011;95:502–508 [DOI] [PubMed] [Google Scholar]
- 20. Weinreb RN, Khaw PT. Primary open-angle glaucoma. Lancet. 2004;363(9422):1711–1720 [DOI] [PubMed] [Google Scholar]
- 21. Anderson DR, Drance SM, Schulzer M. Natural history of normal-tension glaucoma. Ophthalmology. 2001;108(2):247–253 [DOI] [PubMed] [Google Scholar]
- 22. Heijl A, Bengtsson B, Hyman L, Leske MC. Natural history of open-angle glaucoma. Ophthalmology. 2009;116(12):2271–2276 [DOI] [PubMed] [Google Scholar]
- 23. Medeiros FA, Zangwill LM, Alencar LM, Sample PA, Weinreb RN. Rates of progressive retinal nerve fiber layer loss in glaucoma measured by scanning laser polarimetry. Am J Ophthalmol. 2010;149(6):908–915 [DOI] [PubMed] [Google Scholar]
- 24. Bengtsson B, Heijl A. A visual field index for calculation of glaucoma rate of progression. Am J Ophthalmol. 2008;145(2):343–353 [DOI] [PubMed] [Google Scholar]
- 25. Strouthidis NG, Gardiner SK, Sinapis C, Burgoyne CF, Garway-Heath DF. The spatial pattern of neuroretinal rim loss in ocular hypertension. Invest Ophthalmol Vis Sci. 2009;50(8):3737–3742 [DOI] [PubMed] [Google Scholar]
- 26. Grewal DS, Sehi M, Greenfield DS. Comparing rates of retinal nerve fibre layer loss with GDxECC using different methods of visual-field progression. Br J Ophthalmol. Published online September 10, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Weinreb RN, Shakiba S, Zangwill L. Scanning laser polarimetry to measure the nerve fiber layer of normal and glaucomatous eyes. Am J Ophthalmol. 1995;119(5):627–636 [DOI] [PubMed] [Google Scholar]
- 28. Weinreb RN, Dreher AW, Coleman A, Quigley H, Shaw B, Reiter K. Histopathologic validation of Fourier-ellipsometry measurements of retinal nerve fiber layer thickness. Arch Ophthalmol. 1990;108(4):557–560 [DOI] [PubMed] [Google Scholar]
- 29. Zhou Q, Weinreb RN. Individualized compensation of anterior segment birefringence during scanning laser polarimetry. Invest Ophthalmol Vis Sci. 2002;43(7):2221–2228 [PubMed] [Google Scholar]
- 30. Reus NJ, Zhou Q, Lemij HG. Enhanced imaging algorithm for scanning laser polarimetry with variable corneal compensation. Invest Ophthalmol Vis Sci. 2006;47(9):3870–3877 [DOI] [PubMed] [Google Scholar]
- 31. Sample PA, Girkin CA, Zangwill LM, et al. The African Descent and Glaucoma Evaluation Study (ADAGES): design and baseline data. Arch Ophthalmol. 2009;127(9):1136–1145 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Beckett LA, Tancredi DJ, Wilson RS. Multivariate longitudinal models for complex change processes. Stat Med. 2004;23(2):231–239 [DOI] [PubMed] [Google Scholar]
- 33. Fieuws S, Verbeke G, Molenberghs G. Random-effects models for multivariate repeated measures. Stat Methods Med Res. 2007;16(5):387–397 [DOI] [PubMed] [Google Scholar]
- 34. Chakraborty H, Helms RW, Sen PK, Cohen MS. Estimating correlation by using a general linear mixed model: evaluation of the relationship between the concentration of HIV-1 RNA in blood and semen. Stat Med. 2003;22(9):1457–1464 [DOI] [PubMed] [Google Scholar]
- 35. Zucker DM, Zerbe GO, Wu MC. Inference for the association between coefficients in a multivariate growth curve model. Biometrics. 1995;51(2):413–424 [PubMed] [Google Scholar]
- 36. Lee KJ, Thompson SG. Flexible parametric models for random-effects distributions. Stat Med. 2008;27(3):418–434 [DOI] [PubMed] [Google Scholar]
- 37. Ghosh P, Branco MD, Chakraborty H. Bivariate random effect model using skew-normal distribution with application to HIV-RNA. Stat Med. 2007;26(6):1255–1267 [DOI] [PubMed] [Google Scholar]
- 38. Bandyopadhyay D, Lachos VH, Abanto-Valle CA, Ghosh P. Linear mixed models for skew-normal/independent bivariate responses with an application to periodontal disease. Stat Med. 2010;29(25):2643–2655 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Huang Y, Dagne G. Skew-normal Bayesian nonlinear mixed-effects models with application to AIDS studies. Stat Med. 2010;29(23):2384–2398 [DOI] [PubMed] [Google Scholar]
- 40. Huang Y, Dagne G. A Bayesian approach to joint mixed-effects models with a skew-normal distribution and measurement errors in covariates. Biometrics. May 10 2010 [DOI] [PubMed] [Google Scholar]
- 41. Jara A, Quintana F, Martin ES. Linear mixed models with skew-elliptical distributions: Bayesian approach. Comput Stat Data Anal. 2008;52(11):5033–5045 [Google Scholar]
- 42. Ho RKW, Hu I. Flexible modelling of random effects in linear mixed models: a Bayesian approach. Comput Stat Data Anal. 2008;52(3):1347–1361 [Google Scholar]
- 43. Verbeke G, Lesaffre E. A linear mixed-effects model with heterogeneity in the random-effects population. J Am Stat Assoc. 1996;91:217–221 [Google Scholar]
- 44. Verbeke G, Lesaffre E. The effect of misspecifying the random-effects distribution in linear mixed models for longitudinal data. Comput Stat Data Anal. 1997;23:541–556 [Google Scholar]
- 45. Lee KJ, Thompson SG. Flexible parametric models for random-effects distributions. Stat Med. 2008;10 27(3):418–434 [DOI] [PubMed] [Google Scholar]
- 46. Kotz S, Nadarajah S. Multivariate Distributions and Their Applications. Cambridge, UK: Cambridge University Press; 2004 [Google Scholar]
- 47. Fernandez C, Steel MFJ. On Bayesian modeling of fat tails and skewness. J Am Stat Assoc. 1998;93(441):359–371 [Google Scholar]
- 48. Gelman A. Prior distributions for variance parameters in hierarchical models. Bayesian Anal. 2006;1(3):515–533 [Google Scholar]
- 49. Lunn DJ, Thomas A, Best N, Spiegelhalter D. WinBUGS: a Bayesian modelling framework: concepts, structure, and extensibility. Stat Comput. October 2000:10(4):325–337 [Google Scholar]
- 50. Leung CK, Cheung CY, Weinreb RN, et al. Evaluation of retinal nerve fiber layer progression in glaucoma: a comparison between the fast and the regular retinal nerve fiber layer scans. Ophthalmology. 2011;118:763–767 [DOI] [PubMed] [Google Scholar]
- 51. O'Leary N, Crabb DP, Mansberger SL, et al. Glaucomatous progression in series of stereoscopic photographs and Heidelberg retina tomograph images. Arch Ophthalmol. 2010;128(5):560–568 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52. See JL, Nicolela MT, Chauhan BC. Rates of neuroretinal rim and peripapillary atrophy area change: a comparative study of glaucoma patients and normal controls. Ophthalmology. 2009;116(5):840–847 [DOI] [PubMed] [Google Scholar]
- 53. Ang GS, Mustafa MS, Scott N, Diaz-Aleman VT, Azuara-Blanco A. Perimetric progression in open angle glaucoma and the Visual Field Index (VFI). J Glaucoma. 2011;20:223–227 [DOI] [PubMed] [Google Scholar]
- 54. Medeiros FA, Zangwill LM, Bowd C, Sample PA, Weinreb RN. Use of progressive glaucomatous optic disk change as the reference standard for evaluation of diagnostic tests in glaucoma. Am J Ophthalmol. 2005;139(6):1010–1018 [DOI] [PubMed] [Google Scholar]
- 55. Fieuws S, Verbeke G. Pairwise fitting of mixed models for the joint modeling of multivariate longitudinal profiles. Biometrics. 2006;62(2):424–431 [DOI] [PubMed] [Google Scholar]
- 56. Laird NM, Ware JH. Random-effects models for longitudinal data. Biometrics. 1982;38(4):963–974 [PubMed] [Google Scholar]
- 57. Medeiros FA, Alencar LM, Zangwill LM, et al. Detection of progressive retinal nerve fiber layer loss in glaucoma using scanning laser polarimetry with variable corneal compensation. Invest Ophthalmol Vis Sci. 2009;50(4):1675–1681 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Garway-Heath DF, Caprioli J, Fitzke FW, Hitchings RA. Scaling the hill of vision: the physiological relationship between light sensitivity and ganglion cell numbers. Invest Ophthalmol Vis Sci. 2000;41(7):1774–1782 [PubMed] [Google Scholar]
- 59. Medeiros FA, Zangwill LM, Weinreb RN. Improved prediction of rates of visual field loss in glaucoma using empirical Bayes estimates of slopes of change. J Glaucoma. Published online March 16, 2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60. Caprioli J, Miller JM. Correlation of structure and function in glaucoma: quantitative measurements of disc and field. Ophthalmology. 1988;95(6):723–727 [DOI] [PubMed] [Google Scholar]
- 61. Mai TA, Reus NJ, Lemij HG. Structure-function relationship is stronger with enhanced corneal compensation than with variable corneal compensation in scanning laser polarimetry. Invest Ophthalmol Vis Sci. 2007;48(4):1651–1658 [DOI] [PubMed] [Google Scholar]
- 62. Ajtony C, Balla Z, Somoskeoy S, Kovacs B. Relationship between visual field sensitivity and retinal nerve fiber layer thickness as measured by optical coherence tomography. Invest Ophthalmol Vis Sci. 2007;48(1):258–263 [DOI] [PubMed] [Google Scholar]
- 63. Reus NJ, Lemij HG. Relationships between standard automated perimetry, HRT confocal scanning laser ophthalmoscopy, and GDx VCC scanning laser polarimetry. Invest Ophthalmol Vis Sci. 2005;(11):4182–4188 [DOI] [PubMed] [Google Scholar]
- 64. Schlottmann PG, De Cilla S, Greenfield DS, Caprioli J, Garway-Heath DF. Relationship between visual field sensitivity and retinal nerve fiber layer thickness as measured by scanning laser polarimetry. Invest Ophthalmol Vis Sci. 2004;45(6):1823–1829 [DOI] [PubMed] [Google Scholar]
- 65. Strouthidis NG, Vinciotti V, Tucker AJ, Gardiner SK, Crabb DP, Garway-Heath DF. Structure and function in glaucoma: the relationship between a functional visual field map and an anatomic retinal map. Invest Ophthalmol Vis Sci. 2006;47(12):5356–5362 [DOI] [PubMed] [Google Scholar]
- 66. Garway-Heath DF, Holder GE, Fitzke FW, Hitchings RA. Relationship between electrophysiological, psychophysical, and anatomical measurements in glaucoma. Invest Ophthalmol Vis Sci. 2002;43(7):2213–2220 [PubMed] [Google Scholar]