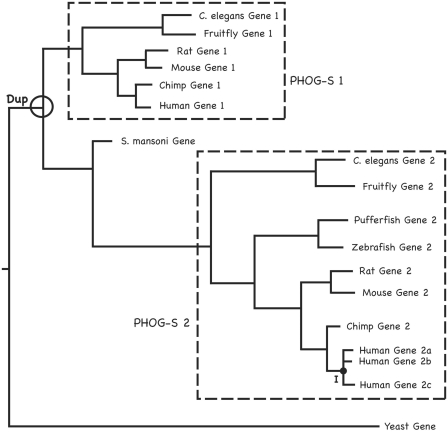
Figure 1:

Orthology and paralogy subtypes and the use of tree distances in PHOG. We present this toy example of gene family evolution to illustrate the main orthology subtypes and how the PHOG algorithm uses tree distances and topology jointly to infer orthologs. ‘Dup’ indicates a duplication event in the animal lineage, and ‘I’ represents a group of predicted inparalogs. Recall that super-orthology requires that all nodes on a path joining two sequences correspond to speciation events. The PHOG algorithm for super-orthology identification allows subtrees containing only members of a single species to be included in a PHOG super-orthology group; some of these will correspond to actual inparalogs while others will be multiple entries and/or isoforms of the same gene in protein sequence databases. The two boxed subtrees (PHOG-S 1 and PHOG-S 2) correspond to super-orthology groups by this definition, with PHOG-S 2 including a possible inparalogous subtree with human genes 2a, 2b and 2c. In contrast, the Schistosoma mansoni and yeast genes have no super-orthologs. Standard phylogenetic orthology prediction protocols consider only the tree topology, including the S. mansoni gene in an orthology group with the Gene 2 clade. However, PHOG uses both tree distance and topology to enhance orthology identification precision; since the tree distances between the S. mansoni gene and genes in PHOG-S 1 are smaller than those between it and genes in PHOG-S 2, it is excluded from PHOG-S 2. This toy example also illustrates the nontransitivity of the standard definition of orthology, which requires only that the most recent common ancestor of two genes correspond to a speciation event. By this definition, the yeast gene is orthologous to Mouse Gene 1 and Mouse Gene 2, and to Rat Gene 1 and Rat Gene 2 and to all of the other sequences in the tree. However, Mouse Gene 1 is clearly not orthologous to Rat Gene 2 (they are paralogs, since they are related by gene duplication).