A possible degree of motional freedom in bacterial chemoreceptor cytoplasmic domains and its potential role in signal transduction

Abstract

We describe an array of gaps in an antiparallel four-helix bundle structure, the cytoplasmic domains of bacterial chemoreceptors. For a given helix, the side chain interactions that define a helix’s position are analyzed in terms of residue interfaces, the most important of which are a-a, g-g, d-d, g-d, and a-d. It was found that the interdigitation of the side groups does not entirely fill the space along the long axis of the structure, which results in a rather regular array of gaps. A simulated piston motion of helix CD1 along the helical axis direction by 1.2Å shows that 85% of the side chain interactions still satisfy Van der Waals criteria, while the remaining clashes could be avoided by small rotations of side chains. Therefore, two states could exist in the structure, related by a piston motion. Analysis of the crystal structure of a small four-helix bundle, the P1_short domain of CheA in Thermotoga Maritima, reveals that the two coexisting states related by a 1.3-1.7Å piston motion are defined by the same mechanism. This two-state model is a plausible candidate mechanism for the long distance signal transduction in bacterial chemoreceptors and is qualitatively consistent with literature chemoreceptor mutagenesis results. Such a mechanism could exist in many other structures with interdigitating α-helices.

Introduction

Bacterial chemotaxis is a well studied model system for studying signal transduction due to its simplicity of architecture, high sensitivity, and broad dynamic range [1, 2]. At the center of the stage is the methyl-accepting chemotaxis protein (MCP), or chemoreceptor, which binds nutrients at the ligand-binding domain and transmits the signal to the signaling tip which can be as far as 300Å away. The signal then passes on to proteins CheA and CheW, which triggers a cascade of events and eventually controls the swimming behavior of the bacteria. MCP is typically composed of ligand binding domain, transmembrane (TM) domain, a linker region (the “HAMP” domain), and cytoplasmic domain (CD) [2]. A number of evidences support the model that the binding of ligand induces a 1-2Å of piston motion of one of the helices (α4/TM2) in the ligand binding and transmembrane domains [3–5].

Less is known about the cytoplasmic domain (MCP-CD), though several hypotheses have been proposed based on certain aspects of experimental results [6–10]. All the proposals are subject to the constraint that the magnitude of the conformation or dynamics change must be small[2] due to the small amplitude of stimulation received from the TM domain[3]. This poses a stark contrast to the large amplitude of thermal motional freedom in the cytoplasmic domain as revealed by many experiments including cysteine reactivity, disulfide formation propensity, NMR chemical shift dispersion, and hydrogen exchange experiments [6, 11]. The current models lack a molecular-level underpinning on the basis of fundamental interactions, which would be necessary to explain how a small signal could survive such large-scale thermal perturbation over a distance as long as 200Å. On the other hand, MCP-CD has a thin, long, and repetitive structure, which only offers very limited modes of motional freedom that can be transmitted along the long axis. In this report, we describe a possible mode of motion in the crystal structures of MCP-CD, compare it with a small four-helix bundle structure with a confirmed two-state behavior, and discuss its potential role in signal transduction.

Methods

The unwinding transformation was performed according to the following procedure. (a) The coordinates of all atoms read from the PDB file are rotated as a rigid body so that the superhelix axis is parallel to z axis. Since both Tsr_c Esc and MCP_1143C are rod-like proteins, the optimal Euler angles for the rotation are found when the z dimension of the protein is maximized and x-y dimension minimized. (b) All the coordinates undergo a translation on the x-y plane so that the center of the superhelix coincides with the origin of the x-y plane.(c) The superhelix is unwound by a rotation about z axis with an angle that is linear to the z position of the atoms. Rotation of 1.91°/Å is used to make all the helices approximately straight. The resulting structure was four straight helices approximately parallel to each other. (d) Coordinates are stored in a new PDB format file and viewed using standard molecular viewing software. All the distance measurements are performed on the original structure, while the unwound structure is only used to make qualitative observations (explicitly noted where they are presented).

It is to be noted that the unwinding transformation is only an aid to easily visualize the structure. All the observations remain the same with or without this transformation.

Results

Packing of chemoreceptor cytoplasmic domain: The cytoplasmic domain crystal structures of Escherichia Coli serine receptor Tsr (Tsr_C Esc, Protein Data Bank code 1QU7) [12] and a chemoreceptor (tm1143) in Thermotoga Maritima (MCP_1143C, Protein Data Bank Code 2CH7) [13] have been determined (the subscripts C stand for cytoplasmic domain). Both of them are four-helix bundles formed by dimers of a pair of antiparallel α helices connected by a “U-turn” at the signaling tip. The four helices are wound together to form a left-handed super helix.

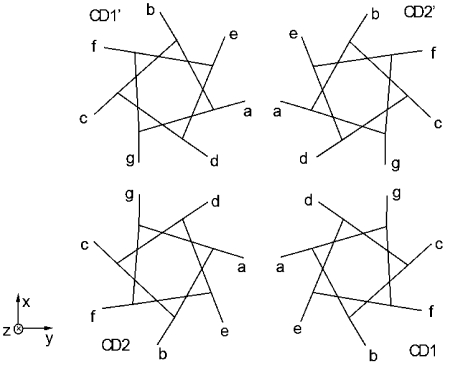
The sequences of MCP-CD exhibit a “double heptad” pattern [12] in which residues a, d, and g are mostly hydrophobic, with d being the most hydrophobic. A sketch of the MCP cross-section is shown on Figure 1, in which the assignment of the heptad positions follows that in ref. [14]. CD1 and CD2 are the N- and C-terminal helix of the first subunit, respectively, while CD1’ and CD2’ belong to the second subunit. The direction of the unwound helix axis toward membrane is defined as z direction, while the cross section of helices as x-y plane. The two subunits have an approximate 2-fold symmetry, so all the discussions on CD1 (CD2) also apply to CD1’ (CD2’). The four helices roughly make a square shape (with deviations in certain sections [10]), with residue d of each helix pointing to the center and residues a and g make up the edges. The relative orientations of the four helices resemble that of knobs-to-knobs packing[8, 15], which is well preserved for all heptads in both crystal structures, with only minor deviations near the signaling tip and the truncated termini. Homology analysis [14] suggests that these packing features and consequently the signal transduction mechanism are likely to conserve for many other chemotaxis systems. Particularly, the crystal structure of Tsr_C ESC and MCP_1143C bear very similar packing features and thus essentially all the discussions on the latter in the present report also apply to the former.

Figure 1.

Cross section sketch of MCP-CD. Each helix is represented by a heptad with residue positions indicated. The extensions projected out of the seven-cornered stars represent the direction of C_α-C_β bonds.

Vacancies in the Protein Structure: First we examine the interaction between a helix and its “lattice” – a collection of all of its direct neighbors. A helix’s position along z direction (referred to as “z position”) is determined by side chain interdigitation with its lattice. Take CD1 of Figure 1 as an example, it interacts with CD2 mainly via residues a from both helices, which have a large interpenetration depth. We call this component of interaction “a_CD1-a_CD2 interface”. CD1 also interacts with CD2 via the e residues of both helices (e_CD1-e_CD2 interface), though this interface is less important in restricting the z position of CD1 than is a_CD1-a_CD2 interface since the pairs of e residues have a smaller average interpenetration depth. By this way, we can decompose the CD1-lattice interaction into the following residue interfaces: a_CD1-a_CD2, g_CD1-g_CD2’, d_CD1-d_CD2’, d_CD1-d_CD2, e_CD1-e_CD2, etc.

To visualize these residue interfaces over many heptads, an algorithm was developed to “unwind” the super-helix, which results in four straight α-helices that are approximately parallel to each other. The unwinding gives a small amount of distortion to the coordinates (a twist of about 10° per turn around the axis of the super helix). This transformation is solely for the convenience of the eye; all the observations discussed in this report have been obtained from the superhelical crystal structure, without invoking this transformation. In addition, all the inter-atomic distance measurements were made from the superhelical structure. All observations made from the unwound structures are specifically stated.

Three most important residue interfaces of MCP_1143C’s CD1, a_CD1-a_CD2, g_CD1-g_CD2’, and d_CD1-d_CD2’, are shown on Figure 2 (unwound structure; sections of 6 heptads for each helix). Only the backbones and the side chains of the involved residues are shown. Interestingly, there is a vacancy (used interchangeably with “gap” in the following) with z dimensions ranging from 1-3Å above (i.e., toward the membrane direction) essentially every CD1 residues for all three interfaces. Due to the array of vacancies, steric repulsion between the side chains at each residue interface does not confine CD1 in a fixed z position. An upward motion of about 1-1.5Å for CD1 along z direction seems to satisfy steric repulsion constraints from all three residue interfaces, resulting in a “free play” room for the entire helix segment.

Figure 2.

Residue interfaces of CD1 (residues 230-269 and 480-516) of the unwound structure. A. a_CD1-a_CD2, B. g_CD1-g_CD2’; and C. d_CD1-d_CD2’. Van der Waals surfaces of the entire backbone and the involved side chains at each interface are displayed. The helix on the left is CD1 in all three panels.

At a given residue interface, each side chain is situated between two side chains (“partners”) from the opposing helix, located on the cytoplasmic (“cyto”) side and membrane (“mem”) side of the side chain, respectively. For example, in Figure 2(a), I238’s cyto- and mem-side partners are V518 and V511, respectively. Table 1 shows the statistics of gap widths for each residue of CD1 formed with its partners at the three major interfaces. The results for the side chains with their partners on the cyto- and mem sides are tabulated separately. The gap width is defined by the closest carbon-to-carbon distance between the pairs of side chains subtracted by 3.8Å. The latter value is the sum of Van der Waals radii of two carbons (1.75Å each) plus 0.3Å, as the lowest-energy distance is about 0.3Å greater than the sum of Van der Waals radii[16]. For residue pairs involving Arg, measurements were taken at γ or δ carbons (depending on which one is closer to its partners) rather than simply by the criterion of shortest distance, as the end group is highly flexible and has little interaction with the backbone.

Table 1.

Asymmetry of CD1 with respect to its cyto- and mem-side partners (measured on structure 2CH7). Gap data for CD1 with mem-side partners are in italic font. Residue pairs that involve Gly do not participate in the average gap width calculation

	aCD1-aCD2		gCD1-gCD2’		dCD1-dCD2’
	cyto	men	cyto	men	cyto	men
total number of residue pairs	21		21		21
Number of pairs with gap width <1Å	14	1	16	4	18	4
Number of pairs with gap width 1Å − 2.5Å	6	13	3	9	1	10
Number of pairs with gap width >2.5Å	1	7	0	6	1	6
Average gap width (Å)	0.66	2.13	0.53	1.79	0.52	2.02

The asymmetry of CD1 with respect to its cyto- and mem side partners is immediately seen from Table 1. Most CD1 side chains are much closer to their partners on cyto side than to those on mem side. Therefore, it appears that the lattice provides more space than what CD1 can occupy, and CD1 is situated in one corner in a span of available space. The results in Table 1 show that the average gap widths for CD1 with its mem-side partners are about the same (~ 2Å) for all three major interfaces, and that the majority of the gaps are between 1.0Å and 2.5Å. This gives rise to the possibility of a piston motion for CD1. Due to the rigidity of α helices, the amplitude of the piston motion of helix CD1 would most likely be relatively uniform for all the involved heptads, probably in the range of 1-1.5Å.This motion also satisfies the constraints from other, less important interfaces not shown on Figure 2. The amplitude of the piston motion is of very similar magnitude for Tsr_C Esc.

The terminology “vacancy” or “gap” rather than “cavity” is used here because there are wide grooves at interfaces e-e and c-c, which can allow water to access a-a and g-g interfaces. In the crystal structure, some water molecules can be seen residing in these grooves. The groove formed between e residues is quite wide (ca. 3Å) and thus can allow water to access interface a-a. The average groove width at c-c interface is slightly smaller than that of e-e. The gap widths at interfaces e-e and c-c are quite uniform for most part of the length except that for the segment within 30Å of the signaling tip, e-e gap width is notably narrower than the size of water molecules.

Several clarifications are to be noted. First, the vacancies as observed in Figure 2 (as well as in Figure 3, discussed later) are not artifacts generated during the unwinding transformation, which only produces an average of 0.2-0.3Å of deviation for most inter-atomic distances and thus does not substantially affect the observations. Residue interfaces generated from the original crystal structures show substantially similar patterns and derive the same conclusions. Second, within the entire range of piston motion, the helix is perfectly in register with the lattice. Finally, while the accuracy of the distance between a single pair of atoms are limited by the resolution and the B-factors of the structures, the observation was made on highly repetitive structures, which makes it relatively safe against errors.

Figure 3.

Interface a_HA-a_HD P1_short of the unwound structure. A. conformer A; B. conformer B, which is related to conformer A by an upward translation of helix HD (right helix), a swing motion of HA (left helix) away from HD, and several side chain rotations.

Analysis of Clashes in a Simulated Motion: A simulation of a piston motion of CD1 was conducted and clashes analyzed. First, in the unwound structure, the z coordinates of all the atoms on CD1 were shifted by 1.2 Å toward the membrane direction. Then the entire structure was rewound to the original state. For each atom, the angle of rewinding as a function of its z coordinate is the negative of the unwinding. This procedure generates a motion that is very close to a piston motion of the superhelical CD1 along the α-helical direction.

The effect of the motion to the average internuclear distances between side chains and their mem-side partners is displayed in Table 2. For interfaces a_CD1-a_CD2, g_CD1-g_CD2’, and d_CD1-d_CD2’, the changes of the distances are similar to the helix shift distance of 1.2Å. This is because these interfaces are highly interpenetrated and thus assume major roles in defining a helix’s z position. For interfaces a_CD1-d_CD2, d_CD1-a_CD2, and g_CD1-d_CD2’, average distances change only slightly, since the z positions of the pairs of residues at these interfaces are quite close. As a result, the extents of interpenetration for the pairs of side chains at these interfaces are small. However, at these interfaces, a given residue is closer to its mem-side partner than to the cyto-side one. This means that a motion toward mem-side would potentially cause overcrowding at these interfaces.

Table 2.

Average closest distances to mem-side partner and the decreases of distances after motion for six interfaces. The distances in the second column are: closest distances between side chain pairs subtraeteci by 3.8Å.

Residue Interface	Average closest distances (Å, from Table 1)	Decrease after motion (Å)
aCD1-aCD2	2.13	1.03
gCD1-gCD2’	1.79	1.14
dCD1-dCD2’	2.02	1.02
aCD1-dCD2	0.24	0.22
dCD1-aCD2	0.34	0.23
gCD1-gCD2’	0.03	0.14

The new structure was analyzed for clashes. The closest distance between two neighboring side chains is used to identify clashes. Two factors were considered to establish criteria for a clash. First, the original crystal structure has a finite resolution and already contains a number of clashes. Second, small clashes may be accommodated by the local flexibility of the α-helices. Precise knowledge of such a tolerance is dependent on many energetic contributions. In the shear model [17], closely packed α-helices may move relative to each other by 1.5Å via small-amplitude side chain rotations. In the current study, we use a stricter criterion and assume a clash of 0.2-0.3Å may be tolerated without significant penalty. For these reasons, we define two criteria for clashes: the distance after motion is (1) less than 3.6Å and (2) more than 0.3Å smaller than that before the motion.

Using the criteria, of the 6 interfaces totaling 126 residue pairs, a total of 19 clashes were identified. This means that for MCP_1143C structure, a piston motion of 1-1.5Å would only encounter sporadic resistances. 85% of the interdigitating residue pairs does not pose a hindrance to the hypothesized motion, while the remaining 15% does. All the clashed pairs consist of at least one large residue (I, L, M, F, N, or E). 12 of the 19 clashes are located in the chemical adaptation domain. A close examination of the side chain packing in the crystal structures suggests that these clashes could be resolved via rotation of the relatively flexible γ or higher side groups, with small enthalpic penalty.

A Two-State Four-Helix Bundle Structure: The 0.98Å resolution crystal structure of P1_short domain of CheA in Thermotoga Maritima was recently published [18]. It shows as structural heterogeneity two states of approximately the same population, and related by a 1.3-1.7Å helical translation of helix HD. A lateral motion of HA and a number of side chain rotamer transitions also accompany the piston motion. To examine how these motions are related, the interaction between HD and its lattice was analyzed by residue interface decomposition. The a_HA-a_HD interfaces of the unwound P1_short for both states are shown on Figure 3. Several observations can be made. First, the locations of both states are determined by the side-chain re-association mechanism discussed above. In conformer A, the associated pairs are V10/V99 and L24/V92, with the closest carbon-to-carbon distance within each pair being 3.40Å and 3.41Å, respectively. In conformer B, the associated pairs are V10/V99, L17/V85, and L24/L92, with the closest carbon-to-carbon distance for each pair being 3.87Å, 4.02Å, and 3.90Å, respectively. Considering the uncertainty of the atomic positions due to the resolution and the B factors of the structure, these distances are very close to the smallest between non-covalent carbons that Van der Waals interaction would allow. The other major residue interface for HD, g_HC-g_HD (not shown), offers little constraint to the HD translation since one key residue at the interface, G91, has no side chain. Second, the two states’ population ratio of nearly unity indicates that they have small energy bias. Third, they are two distinct states rather than a continuum, i.e., they have an energy barrier in between. Finally, at least 11 residues, including V99 (Figure 3), undergo rotamer transition after the piston motion [18].

Discussion

Potential Surface Within the “Free Play”: Of all the clashing side-chain pairs at the six interfaces, each pair involves at least one large side chain, and the clashes occur for atoms at position γ and above. A close look at the crystal structure shows that the clashes could be resolved by rotamer transitions. Detailed analysis of the energetics is beyond the scope of this report, but we may examine two important features in P1_short structure to assist the understanding here.

First, a large number of rotamer transitions occur in company with the piston motion – 11 transitions for a two-heptad-long structure. This implies that for a long structure like MCP_1143C, should the piston motion occur, many side chain rotamer transitions are likely to accompany it, which would be the major mechanism to release clashes. In the cases where the closure of larger (>1.5Å) gaps after the motion are energetically advantageous, it could also be accomplished by side group rotation.

Second, in P1_short, in addition to the piston-like motion, HA also move laterally. Similar lateral motion could also accompany the piston motion of CD1 in MCP. For example, in Table 2, for interfaces a_CD1-d_CD2, d_CD1-a_CD2, and g_CD1-d_CD2, although the decrease of closest-neighbor distances is quite modest, it does push the average distances very close to the limit of Van der Waals repulsion. In such cases, slight lateral motion at certain heptad positions may be feasible.

In addition to side chain rotations, contribution from several other factors to the potential energy surface within the “free play” needs to be discussed. First, estimated using a standard 6-12 formalism [16], the Van der Waals potential surface for a “free play” of around 1.5Å is relatively flat. Second, due to the small widths of the “free play” (ca. two thirds of the gaps are between 1.0 and 2.5Å) compared to the diameter of water molecules (2.8Å), hydrophobic effect should be small even though water molecules can access both of the most important interfaces - a-a and g-g. Finally, water can form energetically favorable interaction with backbone hydrogen-bondable atoms in the vicinity of the gaps. At both ends of the free play, the gaps give space for these interactions to optimize. In the middle, the penetration of water molecules into the vacancies is at a minimum and the interactions have the least room for optimization. As a result, water-helix backbone interaction defines two minima and a potential barrier in between. Since the gap widths are generally smaller than the diameter of a water molecule, the average potential barrier for each gap is probably less than what is required to break a full hydrogen bond. Such an interaction between water and protein surface backbone is often overlooked as it contributes little to protein stability. However, it may play an important role in regulating signal transduction and is likely the dominating contribution to the potential surface in the present case. The total effect of all the interactions defines two minima at both ends of the free play room, where adjacent side chains at each residue interface come in close association to maximize the gap widths.

The potential surface dictates that the protein ensemble must populate both minima, with the relative population determined by the energy bias. The crystal structures of Tsr_C Esc and MCP_1143C display one of the minima, while the other minimum is with CD1 moving toward membrane or CD2 moving toward the opposite direction so that each of its side chain at the interfaces departs from the current associated partner and comes into close contact with the next one (see Figure 4). The possibility of a motional mode in which both CD1 and CD1’ move toward the same direction cannot be excluded as this makes favorable Van der Waals contacts between the d residues of CD1 and CD1’. This piston motion would be able to produce a recognizable conformational change at the signaling tip and trigger the change of kinase activity.

Figure 4.

Transition between the two states via side chain re-association for an α-helix pair.

At each energy minimum, not all the associated side chain pairs are in perfect contacts as idealized on Figure 4. For example, in Figure 2, residue pair L252/L497 at interface a-a and a number of residue pairs at interfaces g-g and d-d are not in perfect contact. Such imperfections are due to two factors: (1) the relative z positions of each side chain in a residue pair are different at different interfaces, since the four-helix bundles are anti-parallel; (2) the sizes of associated residue pairs are different. These imperfections should be tolerable to a certain extent and could even be a mechanism that the bacteria use to adjust the energy bias and energy barrier.

Comparison with mutagenesis experiment results: Extensive mutagenesis studies have been conducted which indicate that the signaling pathway on the cytoplasmic domain can be modified or locked by modification of a single residue at many positions [6, 19-22]. Simon, Parkinson, and coworkers conducted “random” mutagenesis of the entire Tar and Tsr receptor and screened for the mutants that had “locked” signaling states and thus were incapable of chemotaxis [19, 20]. They found that although the nonsense mutations that resulted in dysfunctional chemotaxis were rather evenly distributed throughout the receptor sequences, the missense mutations were highly concentrated in the cytoplasmic domain [19, 20]. This suggests that the signal transduction mechanisms are different between the cytoplasmic domain and other domains, and that the signal in the cytoplasmic domain is more sensitive to single-point mutations. This is consistent with the “free play” mechanism, which requires that the “free play” space be available for every associated side group pair for the signal to pass through, and an increase of side group volume at any point along the way could alter or lock the signal. Mutations with an increase of side chain size on the major interpenetrating residue interfaces (such as a, g, and d) reduce the gap widths. Very bulky side chains could completely fill the free play and thus lock the protein into a fixed state, which could be either of the signaling states or something in between, depending on the particularity of packing. Remarkably, out of the 21 missense mutations of Tsr that occurred in the cytoplasmic domain (residues 295-378 and 402-507, excluding the signaling tip), 18 mutations were on a, d, or g positions [19], which are the most critical positions for the “free play” mechanism. Out of the 18 mutations on a, d, or g positions, 15 involve increases of side group volume, which would block the gaps between the associated side groups and thus jam the “free play”. Given that the “random” mutagenesis approach gives all residues an equal chance to mutate and for each mutation, a roughly equal chance to increase or decrease the side chain volume, the fact that most of the mutants identified for aberrant chemotaxis behavior were on a, d, or g positions strongly support the “free play” mechanism.

Ames et al. found that a soluble Tsr segment (residues 290-470) was able to generate signal to control the swimming behavior of the bacteria [23]. The wild-type segment generated a clockwise (CW) signal, while a single amino acid replacement (A413 to V) generated a counterclockwise (CCW) signal [23]. A413 is in g position, associating with I364 and I371. Due to the large side group volumes of I364 and I371, the free-play room for A413 is small, and mutation to valine would completely jam the free play, in agreement with the finding by Ames et al [23].

Falke and coworkers employed a more systematic mutagenesis approach [6, 21, 22]. The mutations for the buried residues (e.g., at positions a, g, d, and e) often completely lock the signaling state [6], while those for the exposed ones (e.g., at positions b and c) usually only slightly modify the energy bias [6, 22]. These findings were generally consistent with the “free play” mechanism. A glycine substitution study found that out of the 14 highly conserved glycine residues in the cytoplasmic domain of aspartate receptor (Tar) of E. Coli, two are located at the hairpin turn, three are located in a small region which could play a hinge function, and eight others are relatively insensitive to a G-to-A mutation [21]. The insensitivity of most G-to-A mutations on the helices is what would be expected from the “free play” model due to the small side chain volume of alanine.

Thermodynamics of Long-Distance Signal Transduction: The two states related by side chain re-association constitute a qualified system for signaling. Since the geometry of the gaps are similar for both states (Figure 3), a small energy bias [9, 24] is expected, as demonstrated in P1_short. Note that due to the large length of the pathway, even small energy bias and barrier height for each heptad would add up and make the total too high for the small free energy gain upon ligand binding to overcome. This may pose a challenge to the rotation models [8], which would have to balance two large free energy terms of different nature - packing and exposed hydrophobic surface area - over the entire length. The “free play” model also possesses two important attributes: (a) each heptad is a well-defined two-state system and (b) the signaling states of adjacent heptads are coupled due to the rigidity of α helices. They allow the system to use a “domino effect” – transition at one end creates a “push” and triggers the transition of the subsequent heptad, and the transition of the whole pathway is completed via such a relay. It has been known that a conformational state can propagate through polymer crystallites of several hundred angstroms thick, which has a pronounced effect on macroscopic material physical properties [25–27]. The likely mechanism is a propagation of a twisted chain segment involving only a small portion of the entire length, in the form of a solitary wave or soliton [28], therefore the activation energy of the process is substantially lower than that of a rigid body rotation of the entire length. MCP’s could use this mechanism to transmit a signal without a loss, and lower the energy barrier to allow fast switching between states [9]. On the other hand, the coupling of states between neighboring heptads makes the energy barrier high for thermal noise so that it is difficult for the large thermal perturbation [6, 11] to dissipate a signal or activate false ones.

It is clear from the crystal structure that the vacancy (gap) widths are not uniform and the side groups on the interfaces have a variety of sizes. Therefore, for a given signaling state, side chain association is not perfect for all the involved pairs. This should not generate a problem for the definition of the two potential minima since the states of all the heptads are coupled, thus the potential surface for the entire helix is governed by “majority rule”. In fact, perfect side chain association for either state might generate large energy bias, which is undesired for the purpose of signal transduction.

Conditions for the Presence of “Free Play”: The position of an α helix is determined by side chain interdigitation with its lattice, and the length of each heptad is relatively constant but side chains have a variety of sizes. This would dictate that vacancies in a helix bundles are a rule and not an exception. Its implications for many α-helical systems are worth further investigation. On the other hand, since “free play” is a collective result of all the vacancies of a helix formed with its lattice, the requirements for a sizable “free play” are stringent. In the case of MCP-CD, a number of factors are responsible for the large “free play”. First, since a given helix has multiple residue interfaces with the lattice, the arrangement of the heptad packing must be such that this helix’s side chains at all the major interfaces are on the same side of the vacancy. Second, the packing of the four-helix bundle (as depicted in Figure 1) must persist throughout the entire domain. Third, the side chains at the major residue interfaces should be small enough so that there is still vacancy left after filling the space along z direction. For a-a and g-g interfaces, at which the side chain interpenetration is the largest, the most abundant residues are A, V, T, and S. For d-d interfaces, although larger residues such as I and L are more populated, the side chain interpenetration is to a smaller extent. Consequently, for most side chains used at all these interfaces, the interpenetrating part of Van der Waals diameters along z direction mostly ranges from 3.8-5Å. With two side chains filling each heptad (length ≈ 10.8Å) at a given interface, there is usually a gap of 1-2Å left. Such dimensions can be clearly seen in Figure 2.

Therefore, the dimension of the vacancies is dependent on the choice of residues at the interfaces. Large hydrophobic residues (such as I, L, and F) at a highly interpenetrating interface would result in small vacancy width. We can examine two examples, GCN4-pLI [29, 30] and GCN4-pA [15], which are GCN4-based four-helix bundles with parallel and anti-parallel configuration, respectively. GCN4-pLI uses only I and L at the interfaces between neighboring helices. Using the method outlined in “Existence of ‘Free Play’” section and Table 1, the gap widths for a residues of chain A formed with d residues of chain B (interface a_A-d_B) are measured on structure 1U02 [29]. For both directions of helix (equivalent of cyto and mem directions in the case of 2CH7), the average gap widths are only 0.1Å and 0.2Å, respectively. For the interface d_A-d_D of GCN4-pA (2B1F] [15], the average gap widths are 0Å and 0.3Å, respectively. Since the amplitude of “free play” for a chain is decided by the smallest average gap width among all the interfaces, we can conclude that the “free play” is likely non-existent for these two examples. In addition, comparison of the results for these two peptides indicates that the relative orientation between neighboring helices (parallel or anti-parallel) likely does not have a large effect on gap width.

On the other hand, helix HD in P1_short (1TQG) has a substantial “free play” (1.3-1.7Å) despite the presence of relatively large residues at the HA-HD interface, because the large amplitude rotamer transition of V99 helps to provide the required space. Therefore, small average gap width does not necessarily preclude a large “free play” due to the possible role of side chain rotation. However, it does make it difficult to correctly predict the magnitude of “free play” simply from the protein structure.

Relationship with “shear” mechanism: Small translation or “shear” of 1-2Å at the α-helical interfaces is a common mode of motion among both soluble and membrane proteins, including the ligand binding and transmembrane domains of MCP’s [3, 5, 31, 32]. The role of the side chains at the motion interface was thought to take slight torsional angle adjustments to accommodate for domain movements that are initiated by other factors such as ligand binding and hydrogen bond reorganization at the loop regions [32, 33]. The relationship between the “shear” model and the “free play” model has several aspects. First, the “shear” mechanism does not require a specificity of the residues and thus could occur in any α-helical domains, while the “free play” mechanism discussed in this report (at least for those with amplitude ≥1.5Å) requires a “conscious” design of the sequence to work. Therefore, the α-helical domains of most known protein structures probably do not have “free play” that are large enough to be unequivocally discerned. In fact, the “free play” of P1_short is recognized only after the 0.98Å-resolution structure becomes available. Second, in the “shear” mechanism, the two states that are related by small-amplitude side group rotations are within the same local energy minimum. On the other hand, a signaling system requires discrete states, i.e., a potential barrier in between is essential. Therefore, shear mechanism may not be suitable for signal transduction involving long helices, in which the side chain interaction is dominant over the smaller discrete interactions in terms of their contribution to the total potential energy surface. Such a system, when used for long-distance signal transmission, would tend to dissipate the signal and be highly susceptible to thermal noise. In fact, shear motion occurs much less often between parallel helix pairs than crossed pairs [32] due to the enthalpy requirement that is proportional to contact area. Therefore, the shear motion is highly unlikely the working mechanism for such a long helical protein as MCP-CD. On the other hand, in the case of “free play”, a potential barrier is clearly defined between the two states. In the example of P1_short, the side chain re-association pattern and the existence of a potential barrier clearly suggest that the motion belongs to the “free play” class. In these systems, helices take a more “active” role and can form a signaling system by themselves. They can take advantage of the “domino effect” to propagate, multiply, and amplify conformational changes.

It would be of particular interest to examine the signal transduction mechanism in the periplasmic domains of E. Coli chemoreceptors, which has been shown to be via a 1.5Å translation of helix α4 [4, 5]. Unfortunately, several factors make the analysis of the “free play” in this case not straightforward. First, the packing of the domain is not a precisely repetitive four-helix bundle, but a loose dimer of two four-helix bundles [34]. Second, the interfaces involved in the motion (e.g. α1-α4) contain many polar side groups, which introduces the additional complexity due to the re-association of polar or charged groups. Finally, the packing at the residue interfaces lacks the regularity of hydrophobicity and size as seen in the cytoplasmic domains. Therefore, although the “shear” mechanism may play a role here due to its non-specificity, it is not conclusive whether the “free play” mechanism makes a contribution. The relative insensitivity to point mutation of the periplasmic domain in comparison to the cytoplasmic domain [20] seems to suggest that the non-specific “shear” mechanism is the dominating mechanism here.

Relationship between side chain association pattern and kinase activity state: Since only one of the proposed two signaling states is observed in the crystal structures of Tsr_C Esc and MCP_1143C, we would ask whether this observed state corresponds to the kinase-on (apo) or off (holo) state. Several literature results could be examined in relation to this question. Tsr_C Esc crystal structure was obtained on a mutant in which all four methylation sites were mutated with glutamine, which would likely corresponds to kinase-on state [12]. However, all of these sites are close to the terminal region in which the packing largely deviates from that of a normal four-helix. Therefore, it is questionable whether these mutations have an effect on the conformational state of the rest of the cytoplasmic domain. Cells containing isolated Tar cytoplasmic domain fragments indicate that the fragments are in kinase-off state [35]. On the other hand, two isolated wild type Tsr cytoplasmic fragments of slightly different lengths are in opposite signaling states [23]. These results suggest that the signaling state of the cytoplasmic domain is delicately sensitive to many variables, and no firm conclusion could be drawn at the present moment. On the other hand, the unique HAMP domain structure [8]. compared to those of the TM and cytoplasmic domains suggests that the downward piston motion of TM2 upon ligand binding [3] does not necessarily have to continue on to CD1.

Toward a more complete model for signal transduction: There have been more consensus in regard to the signal transduction mechanisms of MCP in the ligand-binding and transmembrane domains. On the other hand, that in the cytoplasmic domain has been elusive and contentious, even though many constraints have been established from the large amount of experimental data. A number of models have been proposed, which describe the signal as a change of helix packing [8], change in the supercoiling of the 4-helix bundle [6], change of dynamics [7], change of trimer orientation [9], change of bending state [10], etc. Each of them is able to interpret certain aspects of the data while faces difficulty accounting for others. It has been recognized that these proposed modes of signal transmission do not necessarily preclude each other but may co-exist to some extent. For example, soluble cytoplasmic fragments of the receptors exhibit locked but varied signaling behavior [23, 35], which suggests that the change of trimer orientation [9] is likely not the only functioning mechanism, but must be accompanied with other mechanism(s) at the intra-dimer level. The “free play” model is also potentially compatible with certain other models, which may lead to a more coherent and complete picture in the future.

Signal transduction by this model does not require the participation of polar or charged side groups, so it may be adopted by the highly hydrophobic transmembrane domains of many membrane proteins, including MCP themselves [3]. It has been observed that the residues responsible for helix-helix interaction in many transmembrane domains are often small residues such as G, A, S, and C [36]. Besides maximizing the interactions between helices and thus stabilizing the structures [36], such choices of residues also could create large vacancy and thus a usable “free play”. This hypothesis may be verified as more and higher-resolution transmembrane domain structures become available.