Medial prefrontal cortex as an action-outcome predictor

Abstract

The medial prefrontal cortex (mPFC) and especially anterior cingulate cortex (ACC) is central to higher cognitive function and numerous clinical disorders, yet its basic function remains in dispute. Various competing theories of mPFC have treated effects of errors, conflict, error likelihood, volatility, and reward, based on findings from neuroimaging and neurophysiology in humans and monkeys. To date, no single theory has been able to reconcile and account for the variety of findings. Here we show that a simple model based on standard learning rules can simulate and unify an unprecedented range of known effects in mPFC. The model reinterprets many known effects and suggests a new view of mPFC, as a region concerned with learning and predicting the likely outcomes of actions, whether good or bad. Cognitive control at the neural level is then seen as a result of evaluating the probable and actual outcomes of one's actions.

The medial prefrontal cortex (mPFC) is critically involved in both higher cognitive function and psychopathology¹, yet the nature of its function remains in dispute. No one theory has been able to account for the variety of mPFC effects observed with a broad range of methods. Initial ERP findings of an error-related negativity (ERN)^{2, 3} have been reinterpreted with human neuroimaging studies to reflect a response conflict detector⁴, and the conflict model⁵ has been enormously influential despite some controversy. Nonetheless, monkey neurophysiology studies have found mixed evidence for pure conflict detection^{6, 7} and have instead highlighted reinforcement-like reward and error signals^7–11. Theories of mPFC function have multiplied beyond response conflict theories to include detecting discrepancies between actual and intended responses¹² or outcomes^{7, 13}, predicting error likelihood^{14, 15}, detecting environmental volatility¹⁶, and predicting the value of actions^{17, 18}. The diversity of findings and theories has led some to question whether the mPFC is functionally equivalent across humans and monkeys¹⁹, despite the fact that monkey fMRI reveals similar effects in mPFC relative to comparable tasks in humans²⁰. Thus a central open question is whether all of these varied findings can be accounted for by a single theoretical framework. If so, the strongest test of a theory is whether it can provide a rigorous quantitative account and yield useful predictions. In this paper we aim to provide such a quantitative model account.

The model begins with the premise that the medial prefrontal cortex (mPFC), and especially the dorsal aspects, may be central to forming expectations about actions and detecting surprising outcomes²¹. A growing body of literature casts mPFC as learning to anticipate the value of actions. This requires both a representation of possible outcomes and a training signal to drive learning as contingencies change¹⁶. New evidence suggests that mPFC represents the various likely outcomes of actions, whether positive⁹, negative^{14, 15}, or both^{22, 23}, and signals a composite cost-benefit analysis^{24, 25}. This proposed function of mPFC as anticipating action values^{17, 18} is distinct from the role of orbitofrontal cortex in signaling stimulus values²⁶. For mPFC to learn outcome predictions in a changing environment, a mechanism is needed to detect discrepancies between actual and predicted outcomes and update the outcome predictions appropriately. A number of studies suggest that mPFC, and anterior cingulate cortex (ACC) in particular, signal such discrepancies^{7, 10, 27, 28}. Recent work further suggests that distinct effects of error detection, prediction and conflict are localized to the anterior and posterior rostral cingulate zones²⁹.

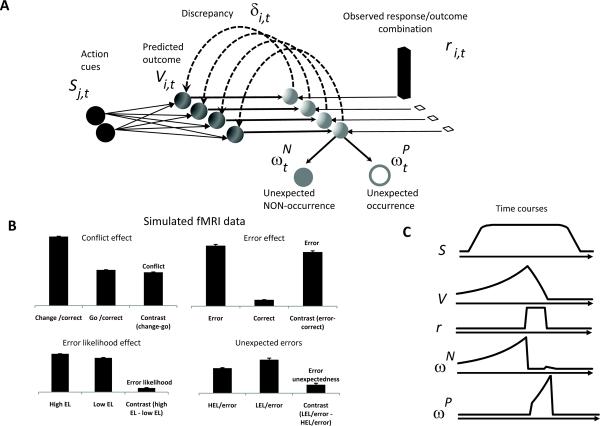
Given the above, we propose a new theory and model of mPFC function, the predicted response-outcome (PRO) model (Fig.1a), to reconcile these findings. The model suggests that individual neurons generate signals reflecting a learned prediction of the probability and timing of the various possible outcomes of an action. These prediction signals are inhibited when the corresponding predicted outcome actually occurs. The resulting activity is therefore maximal when an expected outcome fails to occur, which suggests that mPFC signals in part the unexpected non-occurrence of a predicted outcome.

Figure 1. (A) The Predicted Response Outcome (PRO) model.

In an idealized experiment, a task-related stimulus (S) signaling the onset of a trial is presented. Over the course of a task, the model learns a timed prediction (V) of possible responses and outcomes (r). The temporal difference learning signal (δ) is decomposed into its positive and negative components (ω^P and ω^N, respectively), indicating unpredicted occurrences and unpredicted non-occurrences, respectively. (B) ω^N accounts for typical effects observed in mPFC from human imaging studies. Conflict and error likelihood panels show activity magnitude aligned on trial onset; error and error unexpectedness panels show activity magnitude aligned on feedback. Model activity is in arbitrary units. EL is error likelihood (HEL=High EL; LEL=Low EL). Error bars indicate standard error of the mean (C) Typical time courses for components of the PRO model.

At its core, the PRO model is a generalization of standard reinforcement learning algorithms

$${\delta }_t=r_{t+1}+\gamma V_{t+1}-V_t$$ 1

that compute a temporal prediction error, δ, reflecting the discrepancy between a reward prediction, V, on successive time steps t and t+1, and the actual level of reward, r. γ is a temporal discount factor (0< γ<1) which describes how the value of delayed rewards is reduced.

The PRO model builds on reinforcement learning as a representative learning law, but this should not be taken to imply that mPFC does reinforcement learning per se. The PRO model differs from standard reinforcement learning algorithms in four ways. First, in contrast to typical reinforcement learning algorithms, the PRO model does not primarily train stimulus-response (S-R) mappings. Instead, it maps existing action plans in a stimulus context to predictions of the responses and outcomes that are likely to result, i.e. response-outcome learning. This change to standard reinforcement learning learning conforms well to reports of single units in macaque ACC which learn action-outcome relationships^{10, 18, 30}. Second, instead of a typical scalar prediction of future rewards and scalar prediction error, the PRO model implements a vector-valued prediction, V_i, and prediction error, δ_i, reflecting the hypothesized mPFC role in monitoring multiple potential outcomes, indexed by i. This allows multiple possible action outcomes to be predicted simultaneously, each with a corresponding probability. Previous influential models of mPFC^{13, 31}, similarly derived from reinforcement learning, employ scalar value and error signals that represent, respectively, a prediction and subsequent prediction error of reward. In these models, and reinforcement learning in general, positive value and error signals represent affectively positive outcomes, while negative value and error signals represent affectively negative outcomes. In contrast, the PRO model maintains separate predictions of all possible outcomes, including both rewarding and aversive outcomes. The signed vector prediction error, then, represents unexpected occurrences (positive) or unexpected non-occurrences (negative), regardless of whether these events are rewarding or aversive, and the purpose of these prediction error signals is to provide a training signal to update the predictions of response outcomes. Third, rather than the typical reward signal used in standard reinforcement learning, the model uses a vector signal γ_i which reflects the actual response and outcome combination, again whether good or bad. This enables the PRO model to predict response-outcome conjunctions in proportion to the probability of their occurrence, similar to the Error Likelihood model¹⁵, with the addition that the PRO model learns representations of both rewarding as well as aversive events (for additional detail, see supplementary material). Fourth, and most crucial to the model's ability to account for a wide range of empirical findings, the model specifically detects the rectified negative prediction error defined as when an expected event fails to occur (whether good or bad), for example a reward that is unexpectedly absent. To detect such events, the model computes negative surprise, ω^N, which reflects the probability of an expected outcome that nevertheless did not occur (i.e. unexpected non-occurrence):

$${\omega }_t^N\sum _i\mathit{MAX}(\mathit{Expected}-\mathit{Actual},0)=\sum _i\mathit{MAX}(V_{i,t}-r_{i,t},0)$$ 2

The quantity ω^N reflects the aggregate activity of individual units that compare actual outcomes against the probability of expected response-outcome conjunctions. In equation (2), when the probability of an expected event is higher, its failure to occur leads to a larger negative surprise signal. MPFC activity, then, indexes the extent to which experienced outcomes fail to correspond with outcomes that are predicted, i.e., negative surprise.

While several of the ideas underlying the PRO model have been presented previously in some form, we are not aware of any effort that has brought these ideas to bear simultaneously on the diverse effects observed in mPFC. The unique contribution of this paper, then, is twofold. First, we propose a novel hypothesis that suggests that mPFC signals unexpected non-occurrences of predicted outcomes. Second, we demonstrate that the proposed role of mPFC in monitoring observed outcomes and comparing them against predicted outcomes can account for an unprecedented array of cognitive control, behavioral, neuroimaging, ERP, and single-unit neurophysiology findings, and also provide a priori predictions for future empirical studies.

Results

Representative Tasks

In order to test the ability of the PRO model to account for a diverse range of empirical results, we selected two representative tasks to simulate: the change signal task and the Eriksen Flanker task. These tasks have been widely used in the context of both behavioral and imaging methods, and reliably elicit markers of cognitive control, including increases in reaction time and error rate in behavioral data, and increased activity in brain regions associated with control in imaging data.

At the start of a trial in the change signal task (simulations 1, 2, 4, 5 & 9), a subject is cued to make one of two behavioral responses. On a subset of trials, a second change cue will be displayed shortly following the original cue, instructing the subject to cancel the original response and instead make the alternate response. By manipulating the delay between the original cue and the change cue, specific overall error rates can be obtained.

In the Eriksen Flanker task (simulations 3 & 7), subjects are cued to make one of two behavioral responses by a central target stimulus. Distractor cues are presented simultaneously on both sides of the central stimulus. On congruent trials, the distractors cue the same response as the target cue, whereas on incongruent trials, the distractors cue the alternate response.

Additionally, in order to test the sensitivity of the PRO model to environmental volatility effects¹⁶, we simulate the model in a 2-arm bandit task (simulation 6) similar to a previous report. In the 2-arm bandit task, subjects repeatedly choose from 1 of 2 options which yield rewards at preset rates for each option. In the task simulated, this rate shifts over the course of the experiment, with each option alternately yielding rewards at a high frequency or low frequency.

Our first goal is to ensure that the PRO model can replicate the basic effects observed in mPFC with these tasks and captured by competing models, including error, conflict, and error likelihood effects, as well as the error-related negativity and its relation to speed-accuracy tradeoffs. Second, we seek to show that the PRO model accounts for additional data which are not addressed by competing models, including single-unit activity from monkey neurophysiology studies. In order to ensure that the effects observed in the PRO model do not depend on a specific, manually-tuned parameterization, we initially fit the model to behavioral data from the change signal task. It is essential to bear in mind that the model was only fit to behavioral data, so that all model predictions of ERP, fMRI, and monkey neurophysiology results should be considered qualitative predictions rather than quantitative fits. Except where noted, all simulations reported derive from the model with this single parameter set. Additional details regarding the simulations are given in Methods.

Simulation 1: Error, conflict, and error likelihood effects

In our first simulation, we show that the PRO model can reproduce effects of error, error likelihood, and conflict using the change signal task. Fig. 1b–c show that, over the course of the simulation, the PRO model generates a negative surprise signal corresponding to these effects. The intuition behind error effects is that a correct outcome was predicted, but that prediction signal was not suppressed by signals of an actual correct outcome. Hence the error effect reflects negative surprise, i.e. an unexpected non-occurrence of a correct outcome. Moreover, error effects in the model were stronger for errors made in the low error likelihood condition, consistent with fMRI results not accounted for by previous models^{14, 15}. The PRO model accounts for this effect as activity predicting a correct response is greater in the low error likelihood condition. Thus the absence of a correct outcome when a correct outcome is very likely yields stronger negative surprise. This reasoning applies equally well to findings that the ERN is observed to be larger on error trials in congruent conditions in an Erikson Flanker task¹². For conflict effects, the intuition is that incongruent stimuli signal a prediction of responding to the distractor, in addition to the already strong prediction of a correct response, hence greater aggregate prediction-related activity. The same logic accounts for error likelihood effects: activity representing the prediction of a correct response button-press is already high, and as the probability of an error increases, the activity predicting an additional button-press of the incorrect response also increases proportionally, hence greater aggregate prediction-related activity. Of note, the model suggests a reinterpretation of response conflict effects as not reflecting conflict per se. Rather, conflict effects in the model are due to the presence of a greater prediction of multiple responses, namely the correct and incorrect responses (Simulation 5 below).

Simulation 2: The error-related negativity

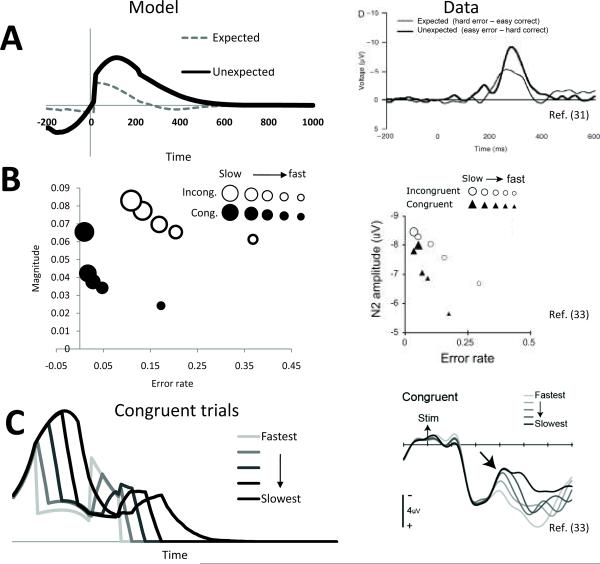
One of the earliest findings in medial prefrontal cortex is the ERN^{2, 3, 13} and the related feedback ERN (i.e. fERN)^{13, 32}, in which the scalp potential overlying mPFC is significantly more negative for errors than correct responses or outcomes. The PRO model simulates the difference-wave fERN, which is not confounded with the P300³¹, as the negative surprise at each time step during a trial. Fig. 2a shows the simulated fERN compared with an actual ERN³¹. The model not only qualitatively simulates the fERN but also simulates the increasing size of the fERN in proportion to the unexpectedness of the error.

Figure 2. ERP simulations.

(A) Left panel: simulated feedback error-related negativity (fERN) difference wave. Effects of surprising outcomes (low error likelihood/error minus high error likelihood/correct) were larger than outcomes which were predictable (high error likelihood/error minus low error likelihood/correct). Right panel: observed ERP difference wave adapted with permission³¹, consistent with simulation results. (B) The effects of speed-accuracy tradeoffs on ERP amplitude are observed in the PRO model (left). Trials for incongruent and congruent conditions were divided into quintile bins by reaction time (large marker indicates slow reaction time, small marker indicates fastreaction time), and activity of the PRO model was calculated for correct trials in each bin. Accuracy and activity of the model were highest for trials with long reaction times, and lowest for trials with short reaction times, consistent with human EEG data (right). (C) The simulated activity of the PRO model (left) reflects amplitude and duration of the N2 component observed in humans EEG studies (right). Adapted with permission³³.

Simulation 3: Speed-Accuracy Tradeoff and the N2

Recent attempts to distinguish between conflict and error likelihood accounts of mPFC function find that the amplitude of the N2 component of the ERP reflects the widely-observed speed-accuracy tradeoff (SATF)³³. The conflict account of the N2 suggests trials with longer RTs reflect longer ongoing competition between potential responses, resulting in higher levels of conflict than for trials with short RTs (although this explanation is not without controversy³⁴). In contrast, the PRO model intuition for this effect is that longer RTs also entail a greater period of time during which the expectation of a correct response is unmet, which in turn yields larger N2 signals. Thus, the model accounts for N2 amplitude effects as a simple positive correlation with RT (Fig. 2c).The PRO model simulates the SATF in a simulated version of a flanker task (Fig. 2b); the negative surprise component of the PRO model is greatest for trials with a relatively long reaction time and is higher for incongruent than congruent trials, as in Simulation 1. The correlation of the simulated amplitude with error rate for the congruent (r=−0.725) and incongruent (r=−0.863) corresponds well with the pattern observed in previously reported data from humans³³.The model further captures how the temporal profile of the N2 component varies with reaction time³³.

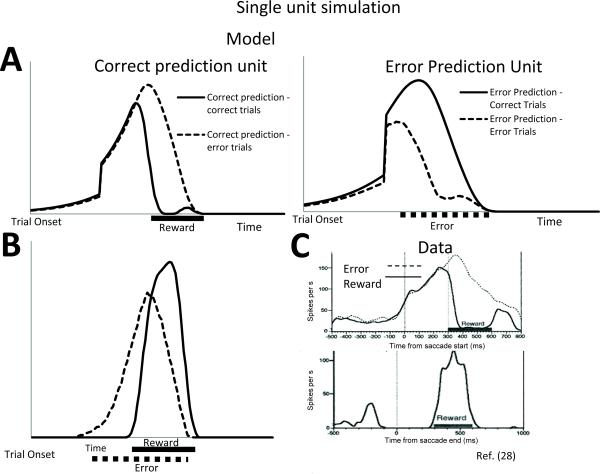
Simulation 4: Monkey single-unit performance monitoring data

Using the change signal task above, we also compared the model predictions with monkey single-unit neurophysiological data. A key challenge to the conflict model of mPFC has been the lack of evidence showing single-unit activity related to conflict in monkey ACC⁷. In contrast, by maintaining multiple predictions of specific response-outcome combinations, single units in the PRO model show activity similar to that of reward and error predicting neurons observed in single-unit neurophysiology data. Fig. 3 shows the average time course of negative surprise (ω^N) and its complement, positive surprise (ω^P, the unexpected occurrence of an outcome, see Methods), which can each reflect predictions of either reward or error outcomes. Similar to activity in monkey supplementary eye field²⁸ (Fig. 3c), signals related to the prediction of reward increase steadily prior to the expected time of reward (Fig. 3a, left). On trials in which the reward is delivered as expected, the negative surprise is suppressed, while on trials in which the reward is not delivered, ω^N peaks around the time of expected outcome and gradually decays. Surprise related to error prediction shows a similar pattern (Fig. 3a, right). Due to the nature of learned temporal predictions in the model, at equilibrium, activity in reward predicting cells will be proportional to the average probability of predicted rewards associated with an outcome^{27, 35}, while activity of error predicting cells will be proportional to the average probability of error associated with an action. Regarding positive surprise, units in mPFC appear to respond to the detection of unpredicted events (Fig. 3b), and the strength with which they respond moderates as the event becomes more predictable^{10, 28, 36}.

Figure 3. Single-unit neurophysiology simulation.

(A) Calculation of the negative surprise signal ω^N was performed for individual outcome predictions (indexed as i). For predictions of e.g. reward, the surprise signal increases steadily to the time at which the reward is predicted. The signal is suppressed on the occurrence of the predicted reward. Single units predicting error follow a similar pattern, with increased variance in the timing of the error. (B) The complement of negative surprise (i.e. positive surprise ω^P) indicates unpredicted occurrences. (C) Reward-predicting and reward-detecting cells recorded in monkey mPFC consistent with simulation results. The top panel displays activity of a single unit consistent with the prediction of a reward. On error trials, activity peaks and gradually attenuates, potentially signaling an unsatisfied prediction of reward. The bottom panel shows single-unit activity related to the detection of a rewarding event. Adapted with permission²⁸.

Simulation 5: Conflict effects as due to multiple responses

The computation underlying response conflict effects in mPFC has been disputed. Early models cast conflict as a multiplication of two mutually incompatible response processes⁵. More recent studies suggest that conflict may arise from a greater number of responses, regardless of mutual incompatibility^{37, 38}. In a recent study³⁷, both the Eriksen flanker task and the change signal task¹⁵ were modified to require simultaneous responses to both distracters and target stimuli. The results showed similar ACC activation in the same region for conditions in which the two possible responses were mutually incompatible as when the responses were required to be executed simultaneously. This suggests that mPFC may signal a greater number of predicted or actual responses or outcomes instead of a response conflict per se, as found previously with neurophysiological studies³⁸.

The PRO model simulates these findings (Fig. 4a) with a modification of the change signal task in which lateral inhibition between response units is removed (see Methods), allowing both responses to be generated simultaneously when a change signal is presented. The PRO model then learns to associate go signals with a high probability of the corresponding anticipated left or right motor response. On trials with a “change” signal, the PRO model generates an additional prediction of the other motor response, which yields an overall net increase in signals predicting the correspondingly greater number of motor responses.

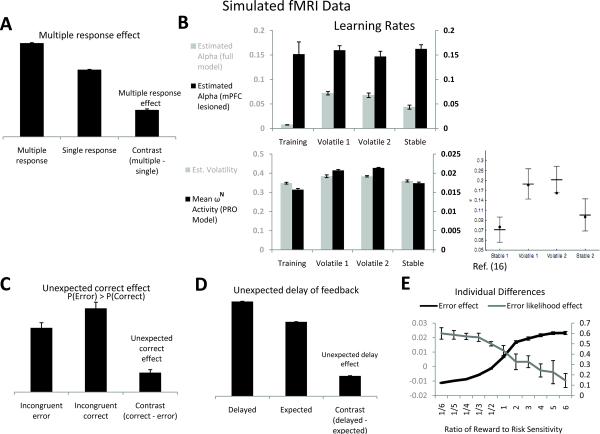
Figure 4. fMRI simulations.

(A) Multiple response effects. The change signal task is modified to require both change and go responses simultaneously when a change signal cue is presented. Change trials lead to greater prediction layer activity (aligned on trial onset) compared with go trials, even though response conflict is by definition absent. The incongruency effect in the absence of conflict is the multiple response effect²³. (B) Volatility effects. When environmental contingencies change frequently, mPFC shows greater activity. This has been interpreted with a Bayesian model in which mPFC signals the expected volatility, right panel (adapted with permission¹⁶). In the PRO model, greater volatility in a block led to greater mean ω^N, lower left panel. Surprise signals, in turn, dynamically modulate the effective learning rate of the model (upper left panel), yielding lower effective learning rates during periods of greater stability (F(1,3)=70.3. p=0.00). In the mPFC-lesioned model, learning rates did not significantly change between periods (F(1,3)=0.23, p=0.88). (C) mPFC signals discrepancies between actual and expected outcomes. If errors occur more frequently than correct trials (70% error rate here), mPFC is predicted to show an inversion of the error effect, i.e. greater activity (aligned on feedback) for correct than error trials. (D) Delayed feedback effect. Feedback that is delayed an extra 400 ms on a minority of trials (20% here) leads to timing discrepancies and greater surprise activation (aligned on feedback). (E) Effects of reward salience on error prediction and detection. As rewarding events influence learning to a greater degree, error likelihood effects (aligned on trial onset) decrease while error effects (aligned on feedback) increase. All error bars indicate standard error of the mean.

Simulation 6: Volatility

A recent Bayesian model of ACC¹⁶ suggests that ACC activity reflects the estimated volatility (non-stationarity) of reinforcement contingencies of an environment. Subjects choosing between two gambles were found to more quickly adapt their strategies (i.e., displayed a higher learning rate) when the probabilities underlying the gambles changed frequently. Moreover, activity in ACC tracked environmental non-stationarity and was higher for subjects with a higher estimated learning rate.

The PRO model fits the observed pattern of greater mPFC activity in non-stationary environments (ω^N, Fig. 4b, lower left panel). Essentially, as contingencies change, the outcome predictions based on the previous contingency persist even as new predictions form based on the new contingencies. As reversals occur, predictions of outcomes made by the PRO model are frequently upset, leading to a state of constant surprise and resulting in more frequent but weaker ω^N signals. This pattern indicates environmental volatility and also serves to drive increased learning during periods of shifting environmental contingencies (Fig. 4b, upper left panel).

Simulation 7: mPFC activity reflects unexpected outcomes

The PRO model reinterprets error effects in mPFC as unexpected outcomes, as distinct from outcomes which are merely undesired. In most human studies, error rates are low. This confounds the interpretation of errors as unintended outcomes with errors as unexpected outcomes. These theories can be distinguished by a manipulation that causes error outcomes to be more likely than correct outcomes. In that case, an error may be expected as the most likely outcome even though it is unintended. If errors reflect unexpected outcomes, then error signals should reverse if correct outcomes are infrequent and therefore unexpected, and correct trials should instead yield greater “error” related activation in mPFC than error trials, and in the same mPFC regions that show error effects. Using a flanker task in which the error rate for incongruent trials was much higher than the rate of correct responses, we tested this prediction and found a striking reversal of the error effect (Fig. 4c), consistent with recent findings^{39, 40}. This result presents a clear challenge to both the conflict account of mPFC function and models of mPFC which are based on standard formulations of reinforcement learning. It is not clear how the conflict account of the ERN can accommodate increased activity in mPFC following correctly executed trials in which behavioral conflict is presumed to be lower than for incorrect trials. Similarly, previous models based on reinforcement learning suggest that mPFC activity reflects only the detection and processing of errors. It is unclear how such a model could account for increased activity in response to correct trials relative to error trials.

Simulation 8: ACC activity reflects unexpected timing of feedback

Single units have been observed in ACC which show precisely timed patterns of activation prior to the occurrence of an outcome^{28, 41}. The PRO model is capable of demonstrating activity consistent with such timed predictions (e.g., Fig. 3a). A further prediction of the model then is that outcomes which occur at unexpected times, even if the outcomes themselves are predicted, will lead to increased ACC activity (Fig. 4d). This prediction suggests another means by which the PRO model may be differentiated from the conflict account, and additional experimental work is needed to test this prediction of the PRO model.

Simulation 9: Individual differences

We tested the effect of the salience of rewarding vs. aversive outcomes by parametrically adjusting the relative influence on learning of error and correct outcomes in the change signal task. The PRO model predicts that individuals who are particularly attentive to rewarding outcomes will exhibit increased mPFC activity in response to error trials (Fig. 4e) compared to individuals who are sensitive to aversive outcomes, while reward-sensitive individuals will exhibit a decrease in activity related to error likelihood (Fig. 4e). In the course of learning, the reward-sensitive model learns predictions primarily about rewarding outcomes, and so exhibits relatively weaker anticipation of errors. Consequently, a greater degree of activity occurs when, on error trials, the strong prediction of reward is not counteracted by the actual reward outcome.

Discussion

Overall, the model suggests a unified account of monkey and human mPFC which builds on widely accepted learning models. The simulation results demonstrate that a single term ω^N, reflecting the surprise related to the non-occurrence of a predicted event, can capture a vast range of cognitive control and performance monitoring effects from multiple research methodologies. These effects have previously been marshaled as evidence in favor of competing theories, especially of conflict and error monitoring in humans, and, conversely, reward prediction and value in monkeys. Thus the PRO model suggests a reconciliation of debates in the literature based on different modalities. The model reinterprets several well-known effects: error effects may represent a comparison of actual vs. expected outcomes, while conflict effects may result from the prediction of multiple possible responses and their outcomes rather than response conflict per se. Strikingly, the model derives these effects from a single mechanism, unexpected non-occurrence, which reflects the rectified negative component of a prediction error signal for both aversive and rewarding events. Furthermore, in the present model, the negative surprise signals consist of rich and context specific predictions and evaluations³⁷. These might drive correspondingly specific proactive and reactive⁴² cognitive control adjustments that are appropriate to the specific context. Finally, the PRO model suggests that within the brain, temporal difference learning signals may be decomposed into their positive and negative components.

The PRO model builds on or relates to a number of existing model concepts, such as the Bayesian volatility model of ACC simulated above¹⁶. The negative surprise signal resembles the unexpected uncertainty signal that has been proposed to drive norepinephrine signals⁴³, although unexpected uncertainty has not been proposed as a signal related to mPFC. The PRO model also resembles models of reinforcement learning in which the value of future states is determined by both the predicted level of reward and the potential actions available to a learning agent. Indeed, others have simulated ERP data related to mPFC with reinforcement learning models^{13, 44}. Examples of other related reinforcement learning models include Q learning and SARSA^{45, 46}. However, these models use a scalar learning signal which combines predicted rewards and possible actions (which may in turn lead to additional rewards) into a composite value prediction. In contrast, our model represents individual rather than aggregate outcome probabilities and includes distinct representations of possible aversive as well as rewarding outcomes. The PRO model further diverges from models of reinforcement learning in that it learns a joint probability of responses and their outcomes for a given stimulus context, P(R,O|S), in contrast to reinforcement learning models that aim to learn the probability of an outcome given a response, P(O|R), in order to select appropriate behaviors. Other reinforcement learning models have been developed with vector rather than scalar based learning signals⁴⁷. While these models are generally concerned with subdividing task control and learning among distinct reinforcement learning controls, the use of a vector-valued learning signal similar to ours has been previously recognized as being necessary for model-based reinforcement learning⁴⁸. However, unlike this previous work, the PRO model suggests that positive and negative components of such a learning signal are maintained independently within the brain. Further comparisons with related models are drawn in the Supplementary Material.

The mPFC signals representing outcome prediction and negative surprise might have several effects on brain mechanisms and behavior. The PRO model currently simulates surprise signals ω^N and ω^P as modulating the effective learning rate for associating a stimulus with its likely responses and outcomes^16,49. The prediction and surprise signals may also serve other roles not simulated here. As an impetus for proactive control, mPFC predictions of multiple likely outcomes may provide a basis for evaluating candidate actions and decisions prior to execution, weighing their anticipated risks¹⁴ against benefits²⁴ especially in novel situations. Similarly, negative surprise signals may provide an important reactive control signal to other brain regions to drive a change in strategy when the current behavioral strategy is no longer appropriate^{8, 50}.

Methods

Computational Model

The PRO model consists of three main components (see supplementary figure S1). The model constitutes a bridge between cognitive control and reinforcement learning theories in that the structure of the model resembles an actor-critic model, with a module responsible for generating actions (the “Actor”) architecturally segregated from a module which generates predictions and signals prediction errors (the “Critic”). An additional module learns a prediction of the frequency with which composite events are observed to occur within a task context (“Outcome Representation”). Unlike typical actor-critic architectures, the critic component is not involved directly in training the actor; rather, the critic indirectly influences the actor's policy by modulating the rate at which predictions of response-outcome conjunctions, which serve as direct input into the actor component, are learned.

Representing events

The Outcome Representation component of the PRO model (Fig. S1) learns to associate observed conjunctions of responses and outcomes with the task-related stimuli that predict them. The number of total conjunctions which are available for learning may vary from task to task depending on the particular responses required and potential outcomes. In the change signal task described below, for example, subjects may either make a 'go' or 'change' response, resulting in 'correct' or 'error' outcomes, for a total of 4 possible response-outcome conjunctions.

The PRO model (Fig. S1) learns a prediction of response-outcome conjunctions (S_i,t) that may occur specifically in the current task, as a function of incoming task stimuli (D_j,t):

$$S_{i,t}={\Sigma }_j{D}_{j,t}{W}_{\mathit{ij},t}^s$$ (1)

Where D is a vector representing current task stimuli, and W^S is a matrix of weights which maintain a prediction of response-outcome conjunctions. S can be thought of as proportional to a conditional probability of a particular response-outcome conjunction given the current trial conditions D. The role of S is to provide an immediate prediction of the likely outcomes of actions and inhibit those that are predicted to yield an undesirable outcome (see equation 11). Prediction weights are updated according to:

$$W_{\mathit{ij},t+1}^s=W_{\mathit{ij},t+1}^s+A_{i,t}(O_{i,t}-S_{i,t})G_t{D}_j$$ (2)

where O is a vector of actual response-outcomes conjunctions occurring at time t, G is a neuromodulatory gating signal equal to 1 if a behaviorally-relevant event is observed and 0 otherwise, and A is a learning rate variable calculated as:

$$A_{i,t}=\frac{\alpha }{1+({\omega }_{i,t}^P+{\omega }_{i,t}^N)}$$ (3)

where α is a baseline learning rate and ${\omega }_{i,t}^P$ and ${\omega }_{i,t}^N$ are measures of positive and negative surprise, respectively (see below).

Temporal Difference Model of Outcome Prediction

In addition to the immediate outcome prediction signals S above that can quickly control behavior, the Critic unit (Fig. S1) also learns a complementary timed prediction of when an outcome is expected to occur. Unlike S, his timed prediction signal V is not immediately active but peaks at the time of the expected outcome. This in turn provides a critical basis for detecting when expected outcomes fail to occur, so that the outcome predictions S that control behavior can be updated. In general, the temporal difference error may be written as follows:

$${\delta }_t=r_t+\gamma V_{t+1}-V_t$$ (4)

where r_t is the level of reward at time t, γ is the temporal discount parameter, constrained by 0 < γ ≤ 1, and V is the predicted value of current and future outcomes, typically rewards. In standard formulations of temporal difference learning, all values are scalars. The PRO model generalizes the temporal difference error by specifying that all variables are vector quantities. In addition, the reward term is replaced with a value which detects the predicted response-outcome conjunction in proportion to the frequency of its occurrence in a given task and for a given model input:

$${\delta }_{i,t}=r_{i,t}+\gamma V_{i,t+1}-V_{i,t}$$ (5)

Here r_i,t is a function of observed response-outcome conjunctions O_i,t. For most simulations, r_i,t = O_i,t except for simulation 9 in which r_i,t = O_i,t × F_i, where F is a constant reflecting the salience of response-outcome conjunction i. In essence, equation (5) specifies a vector-valued temporal difference model that learns a prediction proportional to the likelihood of a given response-outcome conjunction at a given time. Except where noted, γ = 0.95 for all simulations.

As in previous formulations of temporal difference learning, the representation of task-related stimuli over time is modeled as a tapped delay chain, X, composed of multiple units, indexed by j, whose activity (value set to 1) tracks the number of model iterations (“time”) elapsed since the presentation of a task-related stimulus. Each iteration (dt) represents 10 msec. of real time. Value predictions are computed as:

$$V_{i,t}={\Sigma }_{j,k}{X}_{\mathit{jk},t}\times U_{\mathit{ijk},t}$$ (6)

where j is the delay unit corresponding to the current time elapsed since the onset of a stimulus k and U is the learned prediction weight. Weights are updated according to:

$$U_{\mathit{ijk},t+1}=U_{\mathit{ijk},t}+\alpha {\delta }_{i,t}{\stackrel{‒}{X}}_{\mathit{jk}}$$ (7)

where α is a learning rate parameter and constrained by U_ijk > 0. $\stackrel{‒}{X}$ is an eligibility trace computed as:

$${\stackrel{‒}{X}}_{\mathit{jk},t+1}=X_{\mathit{jk},t}+95{\stackrel{‒}{X}}_{\mathit{jk},t}$$ (8)

Stimulus-Response Architecture

In the Actor unit (Fig. S1), activity in response units C is modeled as:

$$C_{i,t+1}=C_{i,t}+\beta \text{dt}\left(E_{i,t}(1-C_{i,t})-(C_{i,t}+.05)(I_{i,t}+1)\right)+N(0,\sigma )$$ (9)

where dt is a time constant, β is a multiplicative factor, N is Gaussian noise with mean 0 and variance σ. E is the next excitatory input to the response units and I is net inhibitory input to response units. Excitatory input to the response units is determined by:

$$E_{i,t}=\rho {\Sigma }_j{D}_j{W}_{\mathit{ij}}^C$$ (10)

where D are task-related stimuli, W^C are pre-specified weights describing hardwired responses indicated by task stimuli, and ρ is a scaling factor. Note that W^C implement stimulus-response mappings which are the usual target of (model-free) reinforcement learning in other models. Here, learning in the PRO model instead updates outcome predictions S, which provide model-based control of actions C. The model is considered to have generated a behavioral responses when the activity of any response unit exceeds a response threshold Γ. Subsequent response unit activity in a trial that exceeds the threshold is ignored (i.e., is not considered to be a behavioral response), whether it is a different response unit or the same response unit whose activity has returned to sub-threshold levels due to processing noise.

Cognitive Control Signal Architecture

Proactive control

The simulation of the change signal task requires a cognitive control signal based on outcome predictions S, which inhibits the model units that generate responses. The vector-valued control signal derived from predicted outcomes could be extended to provide a variety of different control signals in different conditions. In the present model, inhibition to the response units is determined by

$$I_{i,t}=\psi \left({\Sigma }_j{C}_j{W}_{\mathit{ij}}^I\right)+\varphi \left({\Sigma }_k{S}_k{W}_{\mathit{ik}}^F\right)$$ (11)

where W^I are fixed weights describing mutual inhibition between response units, W^F are adjustable weights describing learned, top-down control from predicted-response-outcome representations, and ψ and ϕ are scaling factors. O is the vector of experienced response-outcome representations (eqs 1 & 2). Adjustable weights W^F are learned by

$$W_{\mathit{ik},t+1}^F=W_{\mathit{ik},t+1}^F+.01\ast C_{i,t}{T}_{i,t}{O}_{k,t}{G}_t{Y}_t$$ (12)

where Y_t is an affective evaluation of the observed outcome. For errors, Y_t = 1; for correct responses, Y_t = −.1. The variable T_i,t implements a thresholding function such that T_i,t = 1 if C_i,t > Γ and 0 otherwise.

Reactive control

Reactive control signals in the model are generated whenever an actual outcome differs from an expected outcome. Their magnitude is greatest when an outcome is most unexpected. Signals from the PRO model corresponding to the two forms of surprise described in the main text are calculated as follows. For the first type, unexpected occurrences, the signal is calculated as:

$${\omega }_{i,t}^P={\Sigma }_i{\lfloor O_{i,t}-V_{i,t}\rfloor }^{+}$$ (13)

while the second type of surprise, unexpected non-occurrence, is calculated as:

$${\omega }_{i,t}^N={\Sigma }_i{\lfloor V_{i,t}-O_{i,t}\rfloor }^{+}$$ (14)

As noted above, ω^P and ω^N are used to modulate the effective learning rate for predictions of response-outcome conjunctions. The formulation of Eq. (3) modulates the learning rate of the model in proportion to uncertainty. In stable environments, infrequent surprises result in large values for ω^P and ω^N, which in turn reduce the effective learning rate, whereas in situations in which the model has only weak predictions of likely outcomes, ω^P and ω^N are relatively weak, resulting in increased learning rates. The rationale underlying this arrangement is that infrequent events, which are associated with increased ACC activity, are likely to represent noise rather than a behaviorally significant shift in environmental contingencies, and therefore an individual should be slow to adjust their behavior.

Model Fitting

Model parameters were adjusted by gradient descent to optimize the least-squares fit between human behavioral and model RT and error rate data. Free parameters and their best-fit values are given in table 1. The model was fit using a Change Signal Task using previously reported behavioral data¹⁵. There are seven free parameters in the model in table 1 and ten data points from the change signal task (eight for reaction time, and two for error rate). These parameters allowed the model to simulate the reaction time and error rate effects in the change signal data. The parameters were then fixed for the remaining simulations unless explicitly stated otherwise. Because the model was only fit to human behavioral data, the key model predictions of fMRI, ERP, and single-unit neurophysiology effects result from the qualitative properties of the model rather than from post-hoc data fits.

Table 1.

Model Parameters

Parameter	Description	Value	Equation
α	Learning rate	0.012	5
Γ	Response threshold	0.313	12
ρ	Input scaling factor	1.764	10
ϕ	Control signal scaling factor	2.246	11
ψ	Mutual inhibition scaling factor	0.724	11
β	Rate coding scaling factor	1.038	9
σ	Variance of noise in control units	0.005	9

The best-fit parameters yielded model behavior that corresponded well with human results. The model was trained on 400 trials of the change signal task. Error rates for the model were 52.03% and 5.2% for the high and low error likelihood conditions respectively, in line with human data. Effects of previous trial type on current trial reaction time were in agreement with human performance. For Go trials in which the previous and current trial were correct, the eight conditions yielded a correlation of r=0.96 (t(1,6)=27.17, p=0.00021) between human and model responses times, indicating that the model captured relevant behavioral effects observed in human data.

Simulation Details

In each simulation, trials were presented at intervals of 3 seconds of simulated time. Trials were initiated with the onset of a stimulus presented to the input vector D. All results presented in the main text were averaged over ten separate runs for each simulated task and reflect the derived measure of negative surprise ω^N, except for Fig. 3b, which reflects positive surprise (ω^P). For results presented in bar graph form or results in which data were otherwise concatenated (simulations 1, 3, 5–8), the value of ω^N for the first 120 iterations (1.2 seconds) of a trial were averaged together when trials were aligned on stimulus onset (blue bars). When data were aligned on feedback (red bars), the value of ω^N was taken from the 20 iterations preceding feedback and 80 iterations following feedback.

Simulations 1–2, 4: Change Signal Task

In the change signal task, participants must press a button corresponding to an arrow pointing left or right. On one-third of the trials, a second arrow is presented above the first, indicating that the subject must withhold the response to the first arrow and instead make the opposite response. The color of the arrows is an implicit cue that predicts the likelihood of error as follows: for conditions with high error likelihood, the onset delay of the second arrow is dynamically adjusted to enforce a high rate of error commission (50%). On trials with low error likelihood, the onset of the second arrow is shortened to allow a lower error rate of 5%. The error effect is the contrast between change/error and change/correct trials; the conflict effect is the contrast between change/correct vs. go/correct trials, and the error likelihood effect is the contrast of correct/go trials between high and low error likelihood color cues.

The model was trained for 400 trials, presented randomly. Four task stimuli were used, indicating trial condition: High Error Likelihood/Go, High Error Likelihood/Change, Low Error Likelihood/Go, Low Error Likelihood/Change. On 'go' trials in either error likelihood condition, the stimulus unit (D) corresponding with the 'go' cue in that condition became active (D(go)=1) at 0 seconds and remained active for a total of 1000ms. On 'change' trials, a second input unit became active at either 130 ms (low error likelihood) or 330 ms (high error likelihood). On change trials, units representing both Go and Change cues were active simultaneously when the change signal was presented.

Simulation 3: Speed-Accuracy tradeoff

The model architecture and parameters were the same as in simulation 1 except that connection weights from stimulus units corresponding to the central cue in a Flanker task were set to 1, while weights corresponding to distractor cues were set to .4., the noise parameter was set to 0.02, and the temporal discount factor was set to .85. The model was trained for 1000 trials on the Eriksen Flanker task. In the Flanker task, subjects are asked to make a response as cued by a central target stimulus. On 'congruent' trials in the task, additional stimuli which cue the same response as the target are presented to either side of the target stimulus. On 'incongruent' trials, the additional stimuli cued an alternate response. Incongruent and congruent trials were presented to the model pseudo-randomly, with approximately 1/2 of all trials being congruent.

Simulation 5: Multiple response effect

The model architecture remained the same as in simulation 1 except that lateral inhibition between response units (eq. 11) was removed to allow simultaneous generation of response. Two input representations were used to represent task stimuli, a 'single response' cue and a 'both response' cue. Hard-wired connections from stimulus representations to response units ensured that the single response cue could only result in generation of the appropriate solitary response, while the both response cue activated both response units at approximately the same rate. The model was trained for 400 trials, with approximately 1/2 of the trials being single response trials.

Simulation 6: Volatility

The model was trained on a 2-arm bandit task¹⁶ in which two responses, each representing a different gamble with different payoff frequencies, were possible. The model was trained in a series of 9 stages, divided into four epochs (Fig. 4b). In the first stage of 120 trials, the payoff frequencies of the two gambles were fixed such that one gamble paid off on 80% of the trials in which it was chosen, while the alternate gamble paid off on 20% of the trials in which it was chosen. Starting on trial 121, these payoff contingenices were switched, so that the first gamble paid off at a rate of 20% and the alternate gamble paid off at a rate of 80%. These contingencies were switched every 40 trials a total of 7 times. Finally, the payoff contingencies were returned to their initial values for the final 180 trials. Top-down control weights, W^C, were fixed such that weights associated with errors were 0.15, and weights associated with correct outcomes were −0.05. This was done so that estimates of learning rates were influenced by updates of response-outcome representations alone, and not influenced by learning related to control.

Fig. 4b, lower left panel, shows the average magnitude of ω^N over the total number of trials in each stage. During initial training, ω^N remains low since learned predictions are rarely upset. During subsequent contingency shifts, ω^N increases for each successive stage, reflecting increased uncertainty about the underlying probabilities of the task. Finally, during the final stage of the task, the average magnitude of ω^N decreases, reflecting increased confidence in the model's predictions. The model's choices and experienced outcomes were used as input to a Bayesian Learner¹⁶ to derive measures of volatility in each phase.

Choice behavior from the PRO model, as well as a version of the PRO model in which surprise signals were suppressed (“lesioned”), were used as input to a reinforcement learning model (see Supplementary Material) to derive effective learning rates. When surprise signals generated by the PRO model were used to modulate learning rates, the model adapted quickly to changing environmental contingencies as compared to more stable periods. In contrast, the lesioned model maintained the same learning rate regardless of environmental instability.

Simulation 7: Unexpected outcomes

The model architecture, task, and parameters were the same as described in simulation 3 except that weights from stimulus input units to response units were set to .5 and 2 for the response associated with, respectively, the central target cue and distractor cues in the Eriksen Flanker task. This manipulation is analogous to increasing the saliency of distractor cues in order to promote increased error rate. The model was simulated for 1000 trials a total of 10 times, and error rates for incongruent trials averaged about 70%. We find that average activity of ω^N on correct, incongruent trials is greater than for error, incongruent trials (Fig. 4c), consistent with the theory of errors as reflecting unexpected non-occurrences of predicted outcomes.

Simulation 8: Unexpected timing

The PRO model simulation predicts that mPFC signals not only unexpected outcomes, but also expected outcomes that occur at an unexpected time. The model architecture was the same as for simulation 5. However, instead of manipulating the number of responses, feedback to the model (always correct) was given either after a short delay (200 ms) on 80% of the trials, while for the remaining 20% of the trials, feedback was given 600 ms after a response was generated. The model was trained on this task for 1000 trials. Fig. 4d shows ω^N averaged over trials for long and short delay intervals, indicating a model prediction that unexpectedly delayed feedback should elicit increased mPFC activity.

Simulation 9: Individual differences

The model, task, and parameters were the same as described for simulation 1, with the exception that the effective salience to events was parametrically manipulated to explore the effect of sensitivity to rewarding and aversive events in the model. The salience factor F (see above) was varied from 0.2857 to 1.7143 for rewarding events, while the factor for aversive events was varied from 1.7143 to .2857, resulting in 11 conditions for which the ratio of reward to risk sensitivity ranged from 1/6 (risk sensitive) to 6 (reward sensitive, Fig. 4e). For each condition, 10 simulated runs were included in calculating the mean for each data point. from 0.2857 to 1.7143 for rewarding events, while simultaneously varying α_i for aversive events from 1.7143 to .2857, resulting in 11 conditions for which the ratio of reward to risk sensitivity ranged from 1/6 (risk sensitive) to 6 (reward sensitive; Fig 4E&F). For each condition, 10 simulated runs were included for each data point.