Short TE 3D Radial Gradient-Echo MRI Using Concurrent Dephasing and Excitation (CODE)

Abstract

Ultrashort echo time (UTE) imaging and sweep imaging with Fourier transformation (SWIFT) are powerful techniques developed for imaging ultrashort T₂ species. However, it can be challenging to implement them on standard clinical MRI systems due to demanding hardware requirements. In this paper the limits of what is possible in terms of the minimum echo time (TE) and repetition time (TR) with 3D radial gradient-echo (GRE) sequences, which can be readily implemented on a standard clinical scanner, are investigated. In addition, a new 3D radial GRE sequence is introduced, called CODE (COncurrent Dephasing and Excitation). The unique feature of CODE is that the initial dephasing of the readout gradient is performed during RF excitation, which allows CODE to effectively achieve echo times on the order of ~0.2 ms and larger in a clinical setting. The minimum TE achievable with CODE is analytically described and compared with a standard 3D radial GRE sequence. CODE was implemented on a clinical 3T scanner (Siemens 3T MAGNETOM Trio), and both phantom and in vivo human knee images are shown for demonstration.

INTRODUCTION

Recently, multiple subspecialty areas of MRI research have experienced a surge of interest in techniques to image spins with very short transverse relaxation times, T₂ and T₂*. For biomedical MRI, the musculoskeletal system in particular contains a majority of short T₂ components in connective tissues such as cortical and trabecular bone, meniscal and labral tissues, ligaments and tendons. Such tissues are not easily detected with conventional MRI sequences. Hence, methods like ultrashort echo-time (UTE) imaging (1,2) and sweep imaging with Fourier transformation (SWIFT) (3,4) have been developed to image tissue water signals with T₂ components as short as 100 – 200 μs. With gradient-recalled echo (GRE) imaging, it is generally assumed that the shortest achievable echo time (TE) is ~2 ms when imaging with a clinical scanner. With UTE and SWIFT on the other hand, the delay (or dead time) between excitation and the start of signal acquisition is made very short by acquiring a free induction decay (FID) instead of a gradient-recalled echo. One point worth mentioning here is that the common use of TE to describe the delay between excitation and FID acquisition is inconsistently defined. We therefore prefer to use the alternative terminology of “acquisition delay” in the description of UTE and SWIFT.

In both UTE and SWIFT, k-space is filled in a radial manner (i.e., with “spokes” radiating out from k = 0). In UTE imaging, after radiofrequency (RF) excitation, data acquisition begins as quickly as possible while the readout gradient is being ramped on, to minimize signal loss and blurring (5). To capture signals from extremely short T₂ spins, UTE is typically implemented with a short RF pulse (which usually necessitates high peak RF amplitude, B₁^max) and high gradient slew rate. The shortest achievable acquisition delay is ~ 20 – 100 μs on most clinical scanners, although ~ 8 μs is the shortest acquisition delay that has been reported (6). UTE also encounters challenges relating to non-uniform sampling as a result of sampling data on the gradient ramp. Gridding of non-uniformly acquired data in k-space is particularly difficult since the gradient ramp is not perfectly linear in many cases and the gradients on different axes can have different temporal responses (7). In SWIFT, the gradient field is constant while acquiring the data in a time-shared manner with the RF excitation. That is, the gradient amplitude is at a constant value while signal is acquired in gaps inserted in a broadband frequency-swept excitation pulse. The acquisition delay is limited only by the time needed for the coil ring down (and up) and to switch between transmit and receive modes. This time can be as short as 2 μs when using the latest electronic components in transmit/receive switches (in single transmit/receive coil configuration) or in pin-diode switches (in separate transmit/receive coil applications).

As a modified version of UTE imaging, water- and fat-suppressed projection MR imaging (WASPI) was also proposed in which the gradient is ramped on prior to the RF pulse and held constant until FID sampling is complete (8). In WASPI and related techniques (9,10), unlike UTE, data is acquired not on the gradient ramp, but on the constant gradient, avoiding the challenging problem of non-uniform sampling. However, since WASPI employs a non-selective square RF pulse in the presence of the gradient, the pulse length has to be very short to minimize the signal variation across the object, due to the sinc-shaped excitation profile of the square pulse. As a result, the requirement for high peak RF (B₁^max) can be more of a limitation for these techniques than for UTE and SWIFT. In addition, due to the FID sampling with a very fast rate (typically, 5 - 25 μs per point), data points close to the origin of k-space are not measured during the dead time of the receiver, and thus, an additional short data collection is sometimes needed to recover the lost points (11-13).

Both UTE and SWIFT rely on achieving superior hardware performance, and as a result, are currently undergoing intense development and testing in many different laboratories. For these reasons, standardized versions of these sequences are not yet widely available on commercial MRI scanners. Many applications, including musculoskeletal studies of tendons, ligaments, and meniscus, require detection of spins with T₂ values only in the 1 – 10 ms range, rather than in the tens to hundreds of microsecond range. In such cases, a GRE sequence using the shortest possible TE may suffice.

The purpose of the present study was therefore to investigate the limits of what is possible in terms of minimum TE and repetition time (TR) with 3D radial GRE imaging using a standard clinical scanner. In addition, a new 3D radial GRE sequence is introduced, called CODE (COncurrent Dephasing and Excitation). As can be recognized from its name, the unique feature of CODE is that the initial dephasing of the readout gradient is performed during RF excitation, which allows CODE to effectively achieve TE ≥ ~0.2 ms on a clinical scanner. In this article, the minimum TE and TR achievable with CODE are analytically described and compared with the more standard 3D radial GRE sequence (rGRE). It is also shown that CODE can be implemented on a clinical 3T scanner, and both phantom and in vivo human knee images are shown for demonstration.

METHODS

Pulse sequence and data acquisition

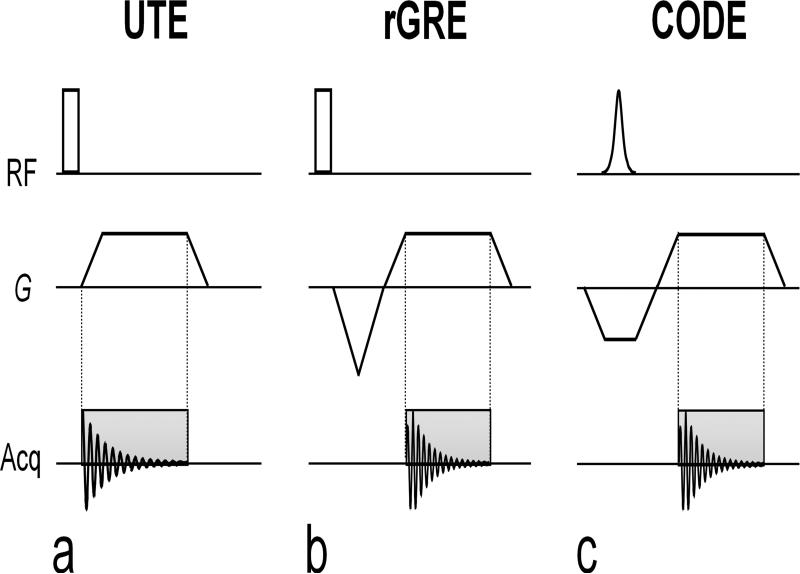
Simplified schematic diagrams of 3D UTE, rGRE, and CODE sequences are shown in Fig. 1. In UTE (Fig. 1a) and rGRE (Fig. 1b), a non-selective square pulse is used for spin excitation, whereas in CODE (Fig. 1c), a shaped pulse is needed to excite a relatively uniform flip angle in the presence of a slab-select gradient (G_ss). The essential feature of the UTE technique is that the FID acquisition begins while ramping up the readout gradient (G_ro) to achieve the shortest possible acquisition delay, without applying an initial dephasing (or pre-dephasing) gradient. Conversely, in rGRE and CODE, immediately following a pre-dephasing gradient which has the opposite polarity of G_ro, a gradient echo is acquired after the readout gradient has reached a plateau. The unique feature of CODE, however, is that slab selection and pre-dephasing are performed with the same gradient. In other words, a pre-dephasing gradient for the frequency-encoded readout is applied during, not after, spin excitation in CODE. Following excitation, acquisition is delayed only by the need to ramp the gradient in one direction, which allows the minimum TE to be less than that of rGRE. In CODE, a frequency-selective RF pulse such as a sinc or a hyperbolic secant pulse (sech/tanh) can be used for the spin excitation in the presence of the slab-select gradient, provided that the thickness of the selected slab is wider than the largest dimension of the object being imaged.

FIG. 1.

Pulse sequence diagrams of 3D UTE, 3D radial GRE (rGRE), and CODE. (a) In the 3D UTE, a square pulse is used for spin excitation and data acquisition starts during the readout gradient ramp to achieve the shortest acquisition delay possible. Since no dephasing gradient is applied for readout, a FID is acquired during acquisition. (b) In rGRE, a square pulse is also used for excitation. Data is acquired during the readout gradient following an initial dephasing (or pre-dephasing) gradient, and thus, a gradient echo is acquired instead of the FID. A partial gradient-echo acquisition scheme is employed to minimize TE. (c) In CODE, slab selection and pre-dephasing are performed with the same gradient. In other words, a pre-dephasing gradient is applied during, not after, spin excitation. Hence, a gradient echo is acquired as in rGRE. A slab-selective pulse such as a sinc or a hyperbolic secant pulse can be used for spin excitation. Because the acquisition time will usually be much longer than the pulse duration (i.e. T_acq is on the order of a few milliseconds or less, whereas T_p is usually ~100 – 300 microseconds), the peak of the gradient echo forms soon after the start of the acquisition period and, thus, the gradient echoes used to fill k-space in each radial direction are asymmetric about the origin of k-space.

In rGRE and CODE, a partial gradient echo acquisition is exploited to minimize TE. The gradient ramps in the x, y, and z axes are required to have the same ramp time (τ) so that the gradients in these axes can start at the same time despite their different amplitudes and thus different rise times. The achievable minimum τ depends on the performance of a gradient system and, in CODE, is equal to the sum of the minimum τ of G_ss and G_ro (Fig. 1c). Here the minimum τ of G_ss and G_ro is given by dividing G_ss and G_ro by the maximum slew rate (SR), respectively. The radial sampling is typically performed with an isotropic angular spacing to cover a sphere in k-space, where the end of the spoke follows a spiral path on the surface of the sphere referred to as view orders (14). Several view-order spirals can be interleaved to increase the total number of projections.

When imaging short T₂ spins with CODE, the pulse length (T_p) is kept as short as possible to achieve the shortest TE within permissible B₁^max and specific absorption rate (SAR) constraints. In the usual implementation of CODE for human studies, T_p is typically ~100 - 300 microseconds, while the acquisition time (T_acq) is much longer, on the order of a few milliseconds or less, depending on the resolution and acquisition bandwidth. In this T_p << T_acq case, the peak of the gradient echo forms soon after the start of the acquisition period. As a result, the gradient echoes used to fill k-space in each radial direction (i.e., the spokes) are asymmetric about the origin of k-space. Due to the asymmetric feature of the gradient-echoes, the highest spatial resolution achieved with rGRE and CODE is given by FOV / {2(n_acq – n_short) – 1}, where FOV is the field-of-view, n_acq is the number of sampled k-space points in data acquisition, n_short is the number of sampled points on the short side of the asymmetric echo.

In the current implementation of rGRE and CODE, images are reconstructed offline using gridding and fast Fourier transformation (FFT). Gridding is performed to distribute the radially sampled data onto Cartesian coordinates by convolving with a Kaiser-Bessel function for interpolation. Then 3D FFT is performed, followed by deapodization which removes the interpolation effect caused by the gridding. For density correction in the gridding process, a two-step iterative gridding/regridding of ones is performed as proposed by Pipe et al. (15). To assign each measurement value to its correct k-space location, each channel was phased separately. Using the phase of the average projection, a single linear function was fitted in a weighted least-squares manner, where the weight was the magnitude of the average projection. From the slope of the linear function, the correct timing of k-space was determined.

The minimum TE achievable with CODE

In this section, the conditions for achieving the shortest TE with CODE are analyzed. For convenience, the slab thickness (THK) is assumed to be the same as the FOV. Under this assumption, the pulse bandwidth (BW) and the acquisition bandwidth (SW) are linearly proportional only to the magnitude of G_ss and G_ro, respectively. In this case, three different situations are considered for the analysis of the shortest TE achievable with CODE, which are: BW > SW (or G_ss > G_ro), BW = SW (or G_ss = G_ro), and BW < SW (or G_ss < G_ro). These are referred to as case 1, 2, and 3, respectively.

To begin, let us compare case 1 (Fig. 2a) with case 2 (Fig. 2b) in terms of achievable minimum TE. With TE defined as the time between the center of the RF pulse and the peak of the echo, in cases 1 and 2,

$$T{E}_{\mathrm{CODE}}=0.5T_{\mathrm{p}}+{\tau }_{\mathrm{ss}}+{\tau }_{\mathrm{ro}}+T_{\text{short}},$$ [1]

where T_short is the duration of the short-side of the asymmetric echo, τ_ss is the ramp time needed for G_ss to reach a plateau (= G_ss/SR), and τ_ro is the ramp time needed for G_ro to reach a plateau (= G_ro/SR). Provided that T_p, SW, and FOV are the same in the two cases, TE₁ > TE₂ because τ_ss,1 > τ_ss,2 and T_short,1 > T_short,2, where subscripts 1 and 2 indicate the case. Here, τ_ss,1 > τ_ss,2 because BW₁ > SW = BW₂, and thus, G_ss,1 > G_ss,2. T_short,1 > T_short,2 can be inferred from the fact that the gradient area with respect to time for pre-dephasing in case 1 is greater than that in case 2, i.e., G_ss,1(T_p/2 + τ_ss,1) > G_ss,2(T_p/2 + τ_ss,2). Therefore, it is concluded that case 2 always offers a shorter TE than case 1.

FIG. 2.

Pulse sequence diagrams of CODE for three different situations, i.e., BW > SW (or G_ss > G_ro), BW = SW (or G_ss = G_ro), and BW < SW (or G_ss < G_ro), which are referred to as case 1 (a), case 2 (b), and case 3, respectively. Particularly in case 3, the gradient area for the pre-dephasing is less than that for the readout, and as a result additional time for dephasing with G_ss is needed to keep the echo peak from occurring during the readout gradient ramp. Two sequence schemes are possible for this purpose. In the case of the basic scheme (c), which is referred to as case 3a, G_ss is simply extended having the same constant value as the original setup. However, in case 3b (d), a part of the extended gradient is replaced with gradient ramps (i.e., ramp-up and ramp-down) with an area (shaded triangle) equal to that of a part of the extended gradient to be replaced (shaded rectangle). The latter always provides a shorter TE than the former by the amount of time corresponding to the width of the shaded rectangle. As proven herein (see text), case 2 provides the shortest TE among the possible schemes, except in some specific circumstances (e.g., small FOV), case 3b provides the shortest TE.

In case 3, the gradient area for the pre-dephasing is less than that for the readout, and as a result additional time for dephasing with G_ss is needed to keep the echo peak from occurring during the readout gradient ramp. As shown in Figs. 2c and 2d, two sequence schemes are possible for this purpose. In the case of the basic scheme (Fig. 2c), which will be referred to as case 3a, G_ss is simply extended in time using the same (constant) G_ss value. However, in case 3b (Fig. 2d), a part of the extended gradient is replaced with gradient ramps (i.e., ramp-up and ramp-down) with an area (shaded triangle) equal to that of the part of the extended gradient to be replaced (shaded rectangle). Case 3b always provides a shorter TE than case 3a by the amount of time corresponding to the width of the shaded rectangle.

Now let us compare case 2 with case 3a. While TE₂ is given by Eq. [1], TE_3a is given by adding the extended dephasing time (τ_ext) to Eq. [1]. Provided that T_p, SW, and FOV (= THK) are the same in the two cases,

$$T{E}_2=0.5T_{\mathrm{p}}+{\tau }_{\mathrm{ss},2}+{\tau }_{\mathrm{ro}}+T_{\text{short},2},$$ [2]

$$T{E}_{3\mathrm{a}}=0.5T_{\mathrm{p}}+{\tau }_{\text{ext}}+{\tau }_{\mathrm{ss},3\mathrm{a}}+{\tau }_{\mathrm{ro}}+T_{\text{short},3},$$ [3]

where T_p,2 = T_p,3 = T_p and τ_ro,2 = τ_ro,3 = τ_ro. In Eq. [3], when it is also assumed that T_short,2 = T_short,3, τ_ext can be expressed in terms of T_p and τ_ss,2 by considering that the gradient area (A) for the predephasing in case 3a has to be equal to that in case 2, i.e., A₂ = A₃. For convenience, τ_ss,3a can be assumed to be ατ_ss,2, where 0 < α < 1, because BW₃ > BW₂ and thus, G_ss,3 > G_ss,2. In this case, the expression for τ_ext in terms of T_p and τ_ss,2 is obtained from the equation A₂ = A₃, which is,

$${\tau }_{\text{ext}}=\frac{1-\alpha }{2\alpha }{T}_{\mathrm{p}}+\frac{1-{\alpha }^2}{2\alpha }{\tau }_{\mathrm{ss},2}.$$ [4]

When using Eqs. [2], [3], and [4], the numerical difference between TE_3a and TE₂ is also given in terms of α, T_p, and τ_ss,2,

$$\Delta T{E}_{3\mathrm{a}}=T{E}_{3\mathrm{a}}-T{E}_2={\tau }_{\text{ext}}+{\tau }_{\mathrm{ss},3}-{\tau }_{\mathrm{ss},2}={\tau }_{\text{ext}}+(\alpha -1){\tau }_{\mathrm{ss},2}=\frac{1-\alpha }{2\alpha }{T}_{\mathrm{p}}+\frac{{(\alpha -1)}^2}{2\alpha }{\tau }_{\mathrm{ss},2}.$$ [5]

Since both first and second terms in Eq. [5] are always positive due to the assumption that 0 < α < 1, TE_3a is always greater than TE₂, and thus, it is concluded that case 2 always provides a shorter TE than case 3a.

Next, let us compare case 2 with case 3b in which a part of the extended G_ss is replaced with gradient ramps. As shown in Fig. 2d, TE_3b is shorter than TE_3a by τ_ss,3a. Thus, TE_3b is obtained by simply subtracting τ_ss,3a from Eq. [3],

$$T{E}_{3\mathrm{b}}=0.5T_{\mathrm{p}}+{\tau }_{\text{ext}}+{\tau }_{\mathrm{ro}}+T_{\text{short},3}.$$ [6]

In this case, the numerical difference between TE_3b and TE₂ is given by

$$\Delta T{E}_{3\mathrm{b}}=T{E}_{3\mathrm{b}}-T{E}_2={\tau }_{\text{ext}}-{\tau }_{\mathrm{ss},2}=\frac{1-\alpha }{2\alpha }{T}_{\mathrm{p}}+\frac{1-2\alpha -{\alpha }^2}{2\alpha }{\tau }_{\mathrm{ss},2},$$ [7]

using Eqs. [2], [4], and [6]. Unlike ΔTE_3a in Eq. [5], ΔTE_3b is not always positive, which means that TE_3b is shorter than TE₂ in some cases. When determining the condition for ΔTE_3b > 0, the constraint needs to be considered that τ_ext should be no less than 2τ_ss,3a in order for the gradient ramp not to begin during the slab-selective excitation, i.e., τ_ext ≥ 2τ_ss,3a (=ατ_ss,2). Because the analysis for ΔTE_3b is complicated and tedious, let us go directly to the conclusion without presenting the detailed description of it here: For α larger than 0.5 (i.e., 0.5 < α < 1), case 2 always provides a shorter TE than case 3b. For α smaller than 0.5 (i.e., 0 < α < 0.5), case 2 provides a shorter TE than case 3b when T_p > 0.5τ_ss,2, which occurs in human applications using a large THK. In the event that T_p < 0.5τ_ss,2, which can be the case in animal studies (e.g., THK ≤ 5.2 cm when T_p = 0.1 ms, BW = 10 kHz, and SR = 170 mT/m/ms), case 3b provides a shorter TE than case 2 for α_i < α < 0.5, where α_i is the point at which ΔTE_3b = 0. In summary, case 2 provides the shortest TE achievable with CODE, except for case 3b when T_p < 0.5τ_ss,2 for α_i < α < 0.5.

In Table 1, the minimum TE values and maximum flip angles achieved with CODE on a 3T Siemens Trio scanner are provided using a knee coil and a body coil. A sinc pulse was used with R = 10, where R is defined as the product of T_p and BW (i.e., R = T_p·BW). n_short was set to be 4. The Siemens phantom D170 with distilled water (including 8.2g NaC₂H₂O₂ + 9.6g C₃H₃O₃Li per 1000g H₂O) was used for coil loading. The minimum TE values were measured for two different FOVs (25 cm and 40 cm), using different T_p values ranging from 0.1 - 0.25 ms in 0.05 ms increments. With T_p = 0.1 ms, the achievable minimum TE was 0.22 ms and 0.18 ms for FOV = 25 cm and 40 cm, respectively, and these were 0.31 ms and 0.27 ms with T_p = 0.25 ms. The maximum flip angles were also measured using the two coils. When using the knee coil, the maximum flip angle was 6° and 12° with T_p = 0.1 ms and 0.25 ms, respectively, and these were 3° and 9° for the body coil. As seen here, when a very short TE is needed, large flip angles cannot be attained with CODE due to the peak B₁ or SAR limitation.

Table 1.

The minimum TE and maximum flip angles achieved with CODE on a 3T MAGNETOM Trio scanner, using a sinc pulse with R = 10.

	FOV (cm)	Pulse length (ms)	Min TE (ms)	Max flip angle (degree)
Knee coil	25	0.10	0.22	6
		0.15	0.26	9
		0.20	0.29	11
		0.25	0.31	12
	40	0.10	0.18	6
		0.15	0.22	9
		0.20	0.25	11
		0.25	0.27	12
Body coil	25	0.10	0.22	3
		0.15	0.26	5
		0.20	0.29	6
		0.25	0.31	9
	40	0.10	0.18	3
		0.15	0.22	5
		0.20	0.25	6
		0.25	0.27	9

*MAGNETOM Trio scanner, using a sinc pulse with R = 10.

The minimum TE achievable with rGRE

In the rGRE sequence (Fig. 1b), spins are excited by a short square pulse which is not slab selective (G_ss = 0), followed by a pre-dephasing gradient (G_deph), and then by G_ro. In order to minimize TE, the pre-dephasing gradient can be replaced by gradient ramps only (i.e., ramp up and ramp down) without a gradient plateau. In this case, the minimum TE is given by

$$T{E}_{\mathrm{rGRE}}=T_{\mathrm{p}}∕2+2{\tau }_{\text{depth}}+{\tau }_{\mathrm{ro}}+T_{\text{short}},$$ [8]

where τ_deph is the ramp time for the pre-dephasing gradient to reach a setup value (τ_deph = G_deph/SR). In the following section, the equations above will be analyzed in detail to determine which sequence, rGRE or CODE, affords the shortest TE values.

Comparison of the minimum TE between CODE and rGRE

Here, it is assumed that peak B₁ or SAR determines the minimum T_p. Hence, in the following comparison of CODE and rGRE, B₁^max or SAR is set equal in the two sequences and set to produce the same flip angle. Under these conditions, the duration of the square pulse used in rGRE will be shorter than that of the frequency-selective pulse (e.g., a sinc) used in CODE. Thus, it is reasonable to assume that the pulse lengths in CODE and rGRE are T_p and cT_p, respectively, where c is the ratio of the pulse length in these two sequences, whereby 0 < c ≤ 1. All the readout parameters such as SW, FOV, τ_ro, and T_short are also assumed to have the same values in both CODE and rGRE.

For the comparison of the minimum TE achievable with CODE (Eq. [1]) and rGRE (Eq. [8]), it is convenient to describe τ_deph in Eq. [8] in terms of τ_ro and T_short, considering that the gradient area of the dephasing (A_deph) is equal to that of the rephasing (A_reph). Given τ_deph = G_deph/SR,

$$A_{\text{deph}}={\tau }_{\text{deph}}\cdot G_{\text{deph}}={\left({\tau }_{\text{deph}}\right)}^2\cdot SR.$$ [9]

On the other hand, A_reph is given by the sum of the area of the gradient ramp and the readout gradient corresponding to T_short, which is,

$$A_{\text{reph}}=0.5{\tau }_{\mathrm{ro}}\cdot G_{\mathrm{ro}}+T_{\text{short}}\cdot G_{\mathrm{ro}}=0.5{\left({\tau }_{\mathrm{ro}}\right)}^2\cdot SR+T_{\text{short}}\cdot {\tau }_{\mathrm{ro}}\cdot SR.$$ [10]

Given A_deph = A_reph (i.e., Eq. [9] = Eq. [10]), τ_deph can be expressed as

$${\tau }_{\text{deph}}={[0.5{\left({\tau }_{\mathrm{ro}}\right)}^2+T_{\text{short}}\cdot {\tau }_{\mathrm{ro}}]}^{1∕2}.$$ [11]

Using Eq. [11] and recalling that the pulse length in rGRE was assumed to be cT_p, the minimum TE achievable with rGRE (Eq. [8]) is rewritten as

$$T{E}_{\mathrm{rGRE}}=0.5\left(c{T}_{\mathrm{p}}\right)+2{[0.5{\left({\tau }_{\mathrm{ro}}\right)}^2+T_{\text{short}}\cdot {\tau }_{\mathrm{ro}}]}^{1∕2}+{\tau }_{\mathrm{ro}}+T_{\text{short}}.$$ [12]

As proven in the previous section, the minimum TE in CODE in most human applications is accomplished with case 2, i.e., when BW = SW. In this case, τ_ss = τ_ro, and thus, the minimum TE in CODE (Eq. [1]) can also be rewritten as

$$T{E}_{\mathrm{CODE}}=0.5T_{\mathrm{p}}+2{\tau }_{\mathrm{ro}}+T_{\text{short}}.$$ [13]

From Eqs. [12] and [13], the condition can be derived for which TE_rGRE = TE_CODE. A quadratic equation in terms of τ_ro is obtained by using the fact that Eq. [12] = Eq. [13], which is,

$${\left({\tau }_{\mathrm{ro}}\right)}^2+[4T_{\text{short}}-(1-c)T_{\mathrm{p}}]\cdot {\tau }_{\mathrm{ro}}-0.25{(1-c)}^2{\left(T_{\mathrm{p}}\right)}^2=0.$$ [14]

Since T_short = T_p/2 in CODE (i.e., in case 2), the coefficient of the second term in Eq. [14] is also expressed in terms of c and T_p. Hence, Eq. [14] is rewritten as

$${\left({\tau }_{\mathrm{ro}}\right)}^2+(1+C)T_{\mathrm{p}}\cdot {\tau }_{\mathrm{ro}}-0.25{(1-c)}^2{\left(T_{\mathrm{p}}\right)}^2=0.$$ [15]

Eq. [15] has two real solutions and its non-trivial solution is

$${\tau }_{\mathrm{ro}}=0.5T_{\mathrm{p}}[-1-c+{(2+2c^2)}^{1∕2}].$$ [16]

Since τ_ro = G_ro/SR = SW/(γFOV·SR), the condition for TE_CODE < TE_rGRE is

$$SW>0.5\gamma FOV\cdot SR\cdot T_{\mathrm{p}}[-1-c+{(2+2c^2)}^{1∕2}],$$ [17]

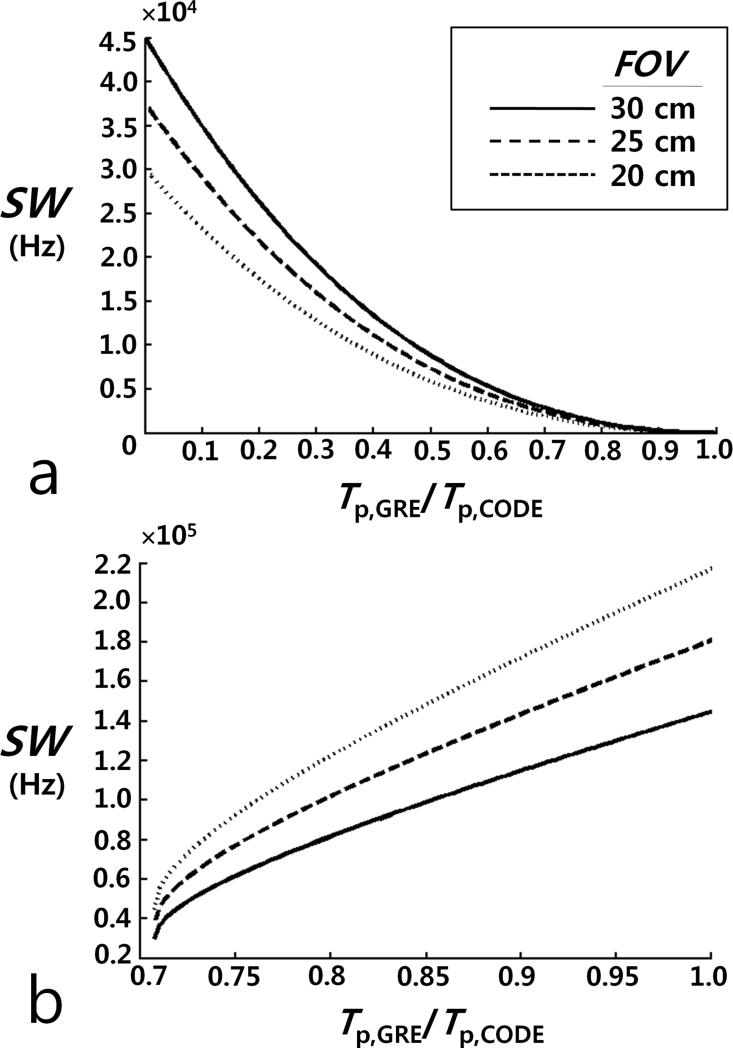
where γ is the gyromagnetic ratio. In Fig. 3a, SW is plotted as a function of c (= T_p,rGRE/T_p,CODE) for different FOV values (= 20, 25, and 30 cm), as c varies between 0 and 1. CODE achieves a shorter TE than rGRE, provided that SW is larger than the plotted value for a given c; that is, when Eq. [17] is satisfied.

FIG. 3.

Plots showing the relationship between SW and the ratio of the pulse length (T_p,GRE) in rGRE to the pulse length (T_p,CODE) in CODE for different FOVs = 20, 25, and 30 cm, (a) when the achievable minimum TE of CODE is equal to that of rGRE and (b) when the achievable minimum TR of CODE is equal to that of rGRE. (a) For a given T_p,GRE/T_p,CODE, CODE provides a shorter TE than rGRE if SW is larger than the plotted value. (b) While CODE has a longer TR than rGRE for T_p,GRE/T_p,CODE < 0.7071, it has a shorter TR than rGRE for T_p,GRE/T_p,CODE ≥ 0.7071, provided that SW is smaller than the plotted value.

Table 2 provides examples of the minimum TE and TR achievable with CODE and rGRE for two different FOVs. For the calculation, a square pulse was used for rGRE and a standard sinc pulse with 3 lobes (R = 10) was used for CODE. The slew rate was set equal to that achievable with a 3T Siemens MAGNETOM Trio system (gradient slew rate = 170 mT/m/ms). A spoiling gradient was not considered for the calculation of TR. A maximum value of 500 Hz was assumed for γB₁/2π, which is a readily attainable value with a whole-body RF coil. The flip angle was set to 3.9° in both pulse sequences. For both CODE and rGRE, BW = SW = 80 kHz, n_acq = 128, and n_short = 4. In CODE, the duration of the sinc pulse (T_p,sinc) was set to be 100 μs. With the same B₁^max value used with the sinc pulse, the duration of the square pulse (T_p,square) is 21.67 μs. In the case of equal SAR produced by sinc and square pulses, T_p,square = 62.07 μs. The minimum TE and TR values that could be achieved with CODE were 0.188 ms and 1.877 ms, respectively, for FOV = 25 cm, and they were 0.155 ms and 1.811 ms for FOV = 40 cm. In the case of the same B₁^max, the minimum TE and TR achievable with rGRE were 0.217 ms and 1.821 ms, respectively, for FOV = 25 cm, and 0.172 ms and 1.759 ms for FOV = 40 cm. In the case of the same SAR, these were 0.238 ms and 1.863 ms, respectively, for FOV = 25 cm, and 0.193 ms and 1.801 ms for FOV = 40 cm. In both cases, as compared with rGRE, CODE has a slightly shorter minimum TE and slightly longer minimum TR. The minimum TE and TR decreases as FOV increases due to the reduction of τ_ss, τ_ro, and τ_dephs.

Table 2.

The minimum TE and TR (in ms) theoretically achievable with CODE and rGRE.

FOV		CODE	rGRE
			same B1max	same SAR
25 cm	TEmin	0.188	0.217	0.238
	TRmin	1.847	1.821	1.863
40 cm	TEmin	0.155	0.172	0.193
	TRmin	1.811	1.759	1.801

*Assumes slew rate of 3T Siemens MAGNETOM Trio scanner (170 mT/m/ms)

EXPERIMENTS

CODE and rGRE sequences were implemented and tested on a clinical 3T MAGNETOM Trio scanner (Siemens, Erlangen, Germany), with a 40 mT/m maximum peak gradient amplitude and a 170 mT/m/ms maximum slew rate. The rGRE and CODE sequence codes were written in-house. In all cases of CODE imaging, a tailored sinc pulse available in the Siemens pulse-shape library was used. This tailored sinc pulse delivers a very flat excitation profile in the pulse bandwidth. A 12-element head coil (Siemens “Head Matrix”) for signal reception in combination with a transmit body coil was used for imaging the resolution phantom. In vivo human knee images were acquired with a transmit/receive birdcage knee coil (Siemens “CP Extremity”). Imaging of normal human volunteers was performed according to the procedure approved by the Institutional Review Board of the University of Minnesota Medical School. For offline image reconstruction, gridding was performed onto two-times oversampled Cartesian grid using a Kaiser-Bessel interpolation kernel with a diameter of 4. No additional corrections were applied to compensate for gradient timing errors and non-linearity, which, however, does not imply that CODE is robust to gradient delays.

Imaging of a resolution phantom (Nuclear Associates 76-903, Fluke Biomedical) was performed to assess the relative image quality and performance of the two sequences. In Fig. 4, phantom images are shown in axial (a and b) and sagittal (c and d) planes. Signal intensity (SI) profiles are also shown along the white solid line in the sagittal images obtained with rGRE (e) and CODE (f), respectively. In all cases, flip angle = 5°, TR = 3.4 ms, FOV (= THK) = 30 cm, and number of projections = 128 k, to achieve 1.0 mm³ isotropic resolution in a scan time of ~6 min. rGRE was performed with TE = 0.22 ms and T_p,square = 0.05 ms. CODE was performed with TE = 0.19 ms and a sinc pulse of duration 0.1 ms (= T_p,sinc) and R = 6.4.

FIG. 4.

Resolution phantom images acquired using rGRE and CODE. Phantom images are shown in axial (a and b) and sagittal (c and d) planes. Signal intensity (SI) profiles are also shown along the white solid line in the sagittal images obtained with rGRE (e) and CODE (f), respectively. In all cases, flip angle = 5°, TR = 3.4 ms, and FOV (= slab width) = 30 cm. The number of projections = 128 k. Scan time = ~6 min. Isotropic resolution = 1.0 mm³. For 3D radial GRE images (a and c), a square pulse was used with T_p,square = 0.05 ms and TE = 0.22 ms. For CODE images (b and d), a sinc pulse was used with T_p,sinc = 0.1 ms and TE = 0.19 ms.

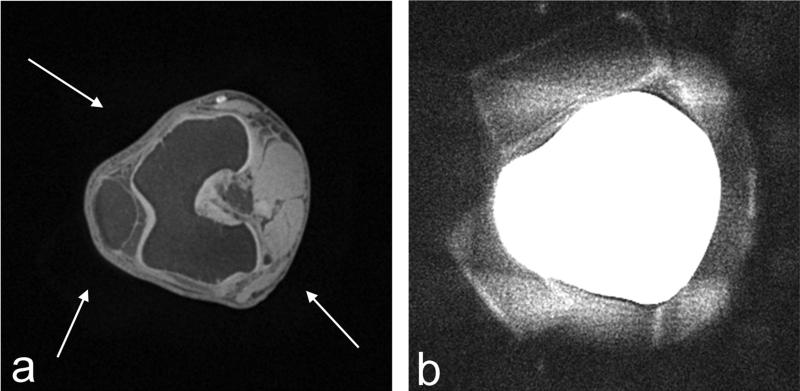
In vivo human knee imaging was also performed using CODE with the shortest TE, i.e., TE = 0.23 ms, which could be practically attained with the 3T Siemens Trio system, when FOV = 25 cm. Fat suppression was performed by applying a spectrally-selective suppression pulse after every 32 acquisitions. A sinc pulse with R = 10 was used for spin excitation. Other parameters were: T_p,sinc = 0.1 ms, flip angle = 4°, and TE = 0.23 ms. The number of projections was 100 k, yielding 0.65 mm³ isotropic resolution in a scan time of ~5 min. To illustrate the general quantity of the 3D imaging, Fig. 5a displays a CODE knee image in an axial view at the level of the patellofemoral joint, which includes anatomical structures such as the patella, femoral lateral and medial trochlear groove articular cartilage, femur, and anterior cruciate ligament insertion at the lateral femoral condyle, along the left-to-right direction. It is worthwhile to note that with a closer look some blurry shades around the knee can be recognized (Fig. 5a, white arrows) which arise from foam pads used to restrict knee movement. These pads, which are in the gap between the knee and the knee coil, are more clearly seen with slice averaging. In Fig. 5b, twenty slices were averaged around the slice shown in Fig. 5a and the averaged image was rescaled for better visualization of the foam padding. While signals from the foam padding are not usually visible with conventional MRI sequences, Fig. 5b illustrates that special attention should be paid to the choice of materials used for supporting structures within the FOV when using ultrashort TE imaging, even when using only modestly short TE of ~0.2 ms.

FIG. 5.

(a) Axial image and (b) slice-averaged and rescaled image of in vivo human knee acquired using CODE with TE = 0.23 ms. T_p,sinc = 0.1 ms, flip angle = 4°, FOV (= THK) = 25 cm, isotropic resolution = 0.65 mm³, and scan time = ~5 min. In (a), an axial knee image was chosen at the level of the patellofemoral joint among the 3D data set, showing an anatomical structure such as the patellar, the femoral lateral and medial trochlear groove articular cartilage, the femur, and the anterior cruciate ligament insertion at the lateral femoral condyle, along the left-to-right direction in the slice. With a closer look, some blurry shades around the knee can be recognized in (a), which are pointed to (white arrows). These signals arise from the foam pads placed between the knee and coil to minimize motion artifacts. These pads are more clearly seen in the image shown in (b) which was obtained by averaging 20 adjacent slices and adjusting the image intensity.

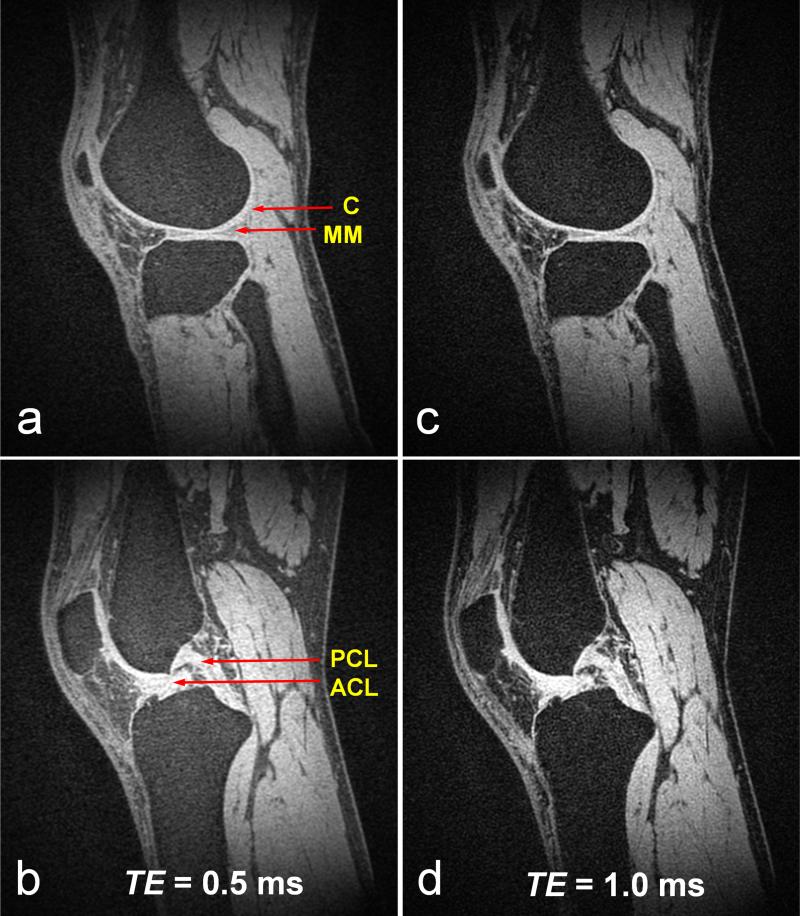
Sagittal images of in vivo human knee acquired using CODE with TE = (a) 0.5 ms and (b) 1.0 ms are shown in Fig. 6. A sinc pulse with T_p,sinc = 0.25 ms and R = 12.7 was used for spin excitation. Other parameters were: flip angle = 4°, TR = 4 ms, and FOV (= slab width) = 25 cm. The number of projections was 128 k, yielding = 0.91 mm³ isotropic resolution in a scan time of ~8 min. Fat suppression was also performed using a spectrally-selective suppression pulse after every 32 acquisitions. With both TE values, CODE provided good sensitivity to visualize connective tissues with a majority of short T₂ components, such as cartilage, anterior and posterior horn medial menisci, patellar tendon, and anterior and posterior cruciate ligament. Although fat signals were generally well suppressed, signals from fatty tissues increased as TE decreased. This may be due to an increasing contribution of short T₂ signal components from fatty tissue as TE decreases.

FIG. 6.

Sagittal images of in vivo human knee acquired using CODE with different echo times, i.e., TE = 0.5 ms in (a) and (b), TE = 1.0 ms in (c) and (d). T_p,sinc = 0.25 ms, flip angle = 4°. TR = 4 ms, and FOV (= slab width) = 25 cm. The number of projections = 128 k. Scan time = ~8 min. Isotropic resolution = 0.91 mm³. Fat suppression was performed using a spectral-selective suppression pulse after every 32 acquisitions. With both TE values, CODE provides good sensitivity for visualizing connective tissues with a majority of short T₂ components, such as cartilage (C) (a, c), anterior and posterior horn medial menisci (MM) (a, c), patellar tendon (a ~ d), and anterior and posterior cruciate ligament (ACL and PCL) (b, d). Despite good suppression of fat signals, signals from fatty tissues increased as TE decreased, which may be due to the increasing contribution of the short T₂ components of fatty tissue.

DISCUSSION AND CONCLUSIONS

The most appealing feature of the two 3D radial GRE sequences described here (rGRE and CODE) is their readiness for implementation on standard clinical MR systems, apparently without placing stringent or unique demands on hardware performance. As shown in this work, these techniques can attain relatively short TE and TR despite the limitations of peak RF power, transmit/receive switching time, coil ring down time, and slew rate that are typical for a standard 3 T clinical scanner. These radial GRE sequences can avoid some of the technical challenges arising from non-uniform sampling that conventional UTE imaging encounters, since data sampling occurs after the gradient has reached a stable plateau. An advantage of 3D MRI is the ability to obtain high-resolution images without missing any information between slices, but 3D MRI has the disadvantage of typically requiring a much longer scan time than 2D imaging. In the case of these radial imaging techniques, however, there are potential ways of reducing the scan time which were not exploited here, e.g., by under-sampling projection trajectories (16,17). In principle, with radial acquisitions, the number of projections, which determines the scan time, does not affect the spatial resolution, but rather affects the size of artifact-free zone.

The CODE sequence has the unique feature that the dephasing lobe of the readout gradient is applied during RF excitation. Such an application of the initial dephasing (or pre-dephasing) gradient during RF excitation enables CODE to offer a much shorter TE than conventional GRE methods and ~15% shorter TE than the rGRE sequence employing a short square pulse. Here it was shown that TE ≥ ~0.2 ms can be achieved in high resolution 3D imaging with a 3T clinical scanner. For example, the achievable shortest TE is 0.22 ms and 0.18 ms for FOV = 25 cm and 40 cm, respectively, as shown in Table 1. Although the theoretically expected minimum TE is 0.19 ms and 0.16 ms for FOV = 25 cm and 40 cm, respectively (Table 2), the shortest TE values that could be attained in this practical setting with a standard clinical scanner are 20 – 30 μs longer than the theoretically expected ones due to some hardware limitations and/or the automatic hardware synchronization inside the system designed to eliminate possible timing errors.

Limitations in CODE

In CODE, a frequency-selective pulse with a very short pulse duration (e.g., a sinc with T_p = 0.1 – 0.2 ms) is used for reducing TE, and thus, a flip-angle restriction is put on CODE. In other words, CODE may be unable to attain large flip angles, i.e., flip angles larger than ~10°, due to the peak B₁ or SAR limitation (Table 1). Thus, although a certain degree of T₁-weighting is possible, extreme T₁-weighted imaging cannot be achieved in human applications with CODE when the shortest TE is desired. Of course, a larger flip angle can also be attained in CODE by increasing T_p at the cost of a longer TE. In this case, TE should be increased by the amount of increase in T_p/2 provided that other parameters remain the same.

Because a frequency-selective pulse is used for excitation in CODE, the initial dephasing gradient for readout must also serve as a slab-selective gradient during excitation. However, strictly speaking, the “real” slab selection does not work for CODE, since it is based on a radial acquisition scheme. In other words, the slab excitation inside an object along a specific direction is not currently feasible because the orientation of the slab changes with every projection. For the same reason, it is also challenging to image a selected region-of-interest (ROI) inside an object by using this slab selection. Recently, ROI reconstruction from limited-angle local projection data, which is called interior reconstruction, was proposed for computed tomography (18,19) and provided the promising possibility that it is applicable to MRI with radial sampling (20). However, the current version of CODE can only be applied to 3D MRI without limiting the FOV by slab selection, and thus, in every direction the excited slab width should exceed the dimensions of the object, unless the sensitive volume is bounded by the sensitivity profile(s) of the local receiver coil(s).

Although CODE cannot attain a TE much less than ~0.2 ms with current clinical scanners, it can be applied to a variety of musculoskeletal studies. Connective tissues, such as meniscus, tendons, ligaments, and cortical bone, contain predominantly bound water with short T₂ values on the order of a few hundreds of microseconds to a few milliseconds (21-23). As demonstrated in the musculoskeletal system in this paper, CODE offers a combination of high SNR with the ability to create differential contrast between tissues dominated by short T₂ components. The images reveal details such as the parallel orientation of the quadriceps tendon fiber bundles, the medial menisci, and the anterior and posterior cruciate ligament. CODE is also potentially useful for dynamic contrast enhanced (DCE) MRI studies at high magnetic fields, since it can effectively reduce T₂*-weighting or signal loss which distorts the time-intensity curve and thus leads to erroneous estimates of pharmacokinetic parameters (24).

This study shows that 3D radial GRE sequences such as rGRE and CODE have the capability of permitting TE as short as ~0.2 ms using a standard clinical scanner. This range of TE is not shorter than that possible with UTE, SWIFT, and WASPI, but it might be sufficient for many types of MRI studies of short T₂ signals. Considering the straightforward implementation and the apparent robustness of these 3D radial GRE sequences, they appear to be promising alternatives to other ultrashort T₂ sequences in certain cases.

Symbols

G_ro

Italic Roman upper case ‘gee’ with subscript Roman lower cases ‘ro’

G_ss

Italic Roman upper case ‘gee’ with subscript Roman lower cases ‘ss’

τ

Greek lower case ‘tau’

T_p

Italic Roman upper case ‘tee’ with subscript Roman lower case ‘pee’

T_acq

Italic Roman upper case ‘tee’ with subscript Roman lower cases ‘acq’

THK

Italic Roman upper cases ‘THK’

THK

Italic Roman upper cases ‘FOV’

BW

Italic Roman upper cases ‘BW’

SW

Italic Roman upper cases ‘SW’

γ

Greek lower case ‘gamma’

TE_CODE

Italic Roman upper cases ‘TE’ with subscript Roman upper cases ‘CODE’

τ_ss

Italic Greek lower case ‘tau’ with subscript Roman lower cases ‘ss’

τ_ro

Italic Greek lower case ‘tau’ with subscript Roman lower cases ‘ro’

τ_ext

Italic Greek lower case ‘tau’ with subscript Roman lower cases ‘ext’

T_short

Italic Roman upper case ‘tee’ with subscript Roman lower cases ‘short’

SR

Italic Roman upper cases ‘SR’

TE₁

Italic Roman upper case ‘TE’ with subscript ‘one’

TE₂

Italic Roman upper case ‘TE’ with subscript ‘two’

τ_ss,1

Italic Greek lower case ‘tau’ with subscript Roman lower cases ‘ss’, coma symbol, ‘one’

τ_ss,2

Italic Greek lower case ‘tau’ with subscript Roman lower cases ‘ss’, coma symbol, ‘two’

T_short,1

Italic Roman upper case ‘tee’ with subscript Roman lower cases ‘short’, coma symbol, one’

T_short,2

Italic Roman upper case ‘tee’ with subscript Roman lower cases ‘short’, coma symbol, ‘two’

BW₁

Italic Roman upper case ‘BW’ with subscript ‘one’

BW₂

Italic Roman upper case ‘BW’ with subscript ‘two’

G_ss,1

Italic Roman upper case ‘gee’ with subscript Roman lower cases ‘ss’, coma symbol, ‘one’

G_ss,2

Italic Roman upper case ‘gee’ with subscript Roman lower cases ‘ss’, coma symbol, ‘two’

TR_CODE

Italic Roman upper cases ‘TR’ with subscript Roman upper cases ‘CODE’

n_acq

Italic Roman lower case ‘en’ with subscript Roman lower cases ‘acq’

n_short

Italic Roman lower case ‘en’ with subscript Roman lower cases ‘short’

R

Italic Roman upper cases ‘aal’

G_deph

Italic Roman upper case ‘gee’ with subscript Roman lower cases ‘deph’

TE_rGRE

Italic Roman upper cases ‘TE’ with subscript Roman lower case ‘aal’, Roman upper cases ‘GRE’

τ_deph

Italic Greek lower case ‘tau’ with subscript Roman lower cases ‘deph’

TR_rGRE

Italic Roman upper cases ‘TR’ with subscript Roman lower case ‘aal’, Roman upper cases ‘GRE’

B₁

Italic upper case ‘bee’ with subscript ‘one’

c

Italic Roman lower cases ‘see’

A_deph

Italic Roman upper case ‘ei’ with subscript Roman lower cases ‘deph’

A_reph

Italic Roman upper case ‘ei’ with subscript Roman lower cases ‘reph’

π

Greek lower case ‘pi’

T_p,sinc

Italic Roman upper case ‘tee’ with subscript Roman lower case ‘pee’, coma symbol, Roman lower cases ‘sinc’

T_p,square

Italic Roman upper case ‘tee’ with subscript Roman lower case ‘pee’, coma symbol, Roman lower cases ‘square’