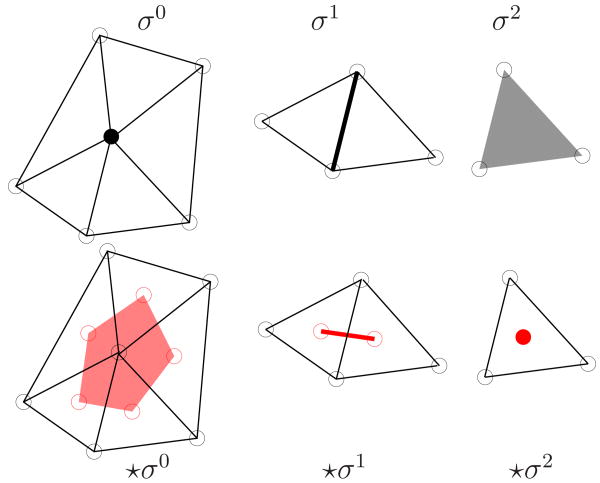
Figure 1.

Primal simplices are shown in black in the top row: σ⁰ is a vertex, σ¹ is an edge, and σ² is a face. Their corresponding dual cells for n = 2 are shown in red on bottom: ⋆σ² is the barycenter of σ², ⋆σ¹ is an edge between barycenters, and ⋆σ⁰ is a planar polygon with barycenters as vertices. In three dimensions (n = 3), primal vertices have dual polytopes, primal edges have dual polygonal facets, primal faces have dual edges, and primal volumes have dual vertices.