Figure 5.

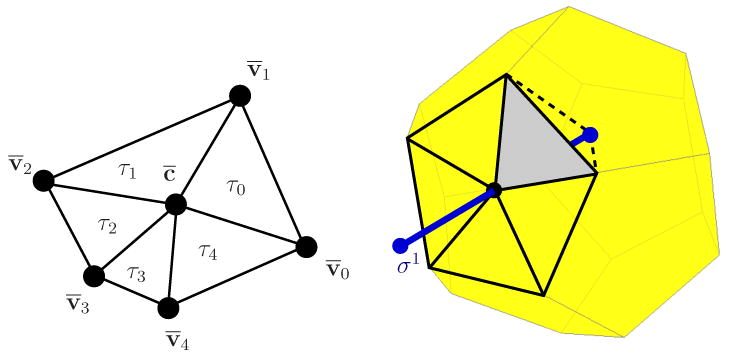
Sample computation of a dual Whitney function associated to a dual face ⋆σ¹ with vertices v̄_i. By adding the centroid c̄, we have a canonical decomposition of ⋆σ¹ into triangles τ_i. A weighted sum of the primal Whitney function associated with each τ_i is constructed to define the function for the face. As shown on the right, each τ_i, e.g. the shaded triangle, forms a tetrahedron by connecting its vertices to the vertex of σ¹ interior to the polyhedron. Note that in general c̄ need not be the same as σ¹ ∩ ⋆σ¹.