Abstract
Purpose: Surface curvatures are important geometric features for the computer-aided analysis and detection of polyps in CT colonography (CTC). However, the general kernel approach for curvature computation can yield erroneous results for small polyps and for polyps that lie on haustral folds. Those erroneous curvatures will reduce the performance of polyp detection. This paper presents an analysis of interpolation’s effect on curvature estimation for thin structures and its application on computer-aided detection of small polyps in CTC.
Methods: The authors demonstrated that a simple technique, image interpolation, can improve the accuracy of curvature estimation for thin structures and thus significantly improve the sensitivity of small polyp detection in CTC.
Results: Our experiments showed that the merits of interpolating included more accurate curvature values for simulated data, and isolation of polyps near folds for clinical data. After testing on a large clinical data set, it was observed that sensitivities with linear, quadratic B-spline and cubic B-spline interpolations significantly improved the sensitivity for small polyp detection.
Conclusions: The image interpolation can improve the accuracy of curvature estimation for thin structures and thus improve the computer-aided detection of small polyps in CTC.
Keywords: curvature estimation, polyp detection, interpolation, Deriche filter
INTRODUCTION
Colonic polyps are known precursors to colon cancer.1 Early detection and removal of polyps may help to reduce the risk of colon cancer. CT colonography (CTC) is a feasible and minimally invasive method for the detection of colorectal polyps and cancer screening.2 Computer-aided detection (CAD) of polyps has improved consistency and sensitivity of CTC interpretation and reduced interpretation burden.3 Typically, a CAD system is used to analyze CTC data automatically by use of image analysis and pattern recognition algorithms, and the locations of detected abnormalities are reported to a physician.
Polyps are growths from the colonic mucosa, the inner wall of the colon. The majority are sessile, appearing such as elliptical protrusions. CAD algorithms may, therefore, detect polyps through their shape. The primary characteristic of this shape is its curvature. Indeed, curvature is the basis of almost all existing CAD schemes for polyp detection.4, 5, 6, 7, 8, 9, 10, 11, 12, 13
In general, there are two approaches (geometry∕surface-based and image-based) to computing curvature estimates from volumetric images. The first approach (geometry∕surface-based) is to fit locally a surface patch to the data, with a known parameterization in a local coordinate system, and to compute surface curvatures from the parameterized surface.14, 15, 16 Unfortunately, it is difficult to obtain a continuous parametric representation of the whole surface when its topology is complicated and not known a priori. In addition, the local model obtained from only surface voxels without using gray value information tends to become noisy. The second approach (image-based) works directly on gray value information by exploiting the local differential structure of the image.17, 18 This approach is also known as a kernel approach, because the partial derivatives are usually computed by convolving the 3D gray value image with Gaussian-like differential kernels.
In the second approach, the iso surface curvature is defined as ITT∕∥ ∇I ∥ (the second derivative along the tangential divided by the gradient magnitude) and is successfully applied to many structures in 3D gray value images,17 but it fails when applied to thin structures. This is due to the fact that: (1) on ridges and in valleys, the gradient ∥∇I∥ is nearly zero; (2) Opposite sides of a ridge (or valley) yield curvatures of opposite sign which cancel out after averaging. When this kernel approach is applied for polyp detection, such problem was pointed out by many researchers.12, 16, 19 That is, spurious estimation of curvatures could be observed in two situations: (1) thin flat folds and small polyps. Here, the “thin” and “small” are relative to the window size of kernel used for curvature estimation. (2) when two structures are residing in a same kernel window. The reason is that those thin folds, small polyps, and boundary of two structures construct ridges and valleys within the kernel.
To address such a problem, Wijk et al.21 use normalized convolution to calculate the first and second-order derivatives, where the different structures were differentiated by using the gradient of a distance transform based on the air-tissue interface. Similarly, Wang et al.12 directly eliminated the contribution of voxels of different structures during the convolution. Zhu et al. applied level-set based adaptive convolution22 and Knutsson mapping method19 to improve curvature estimation for colonic polyps. However, only few or one CT dataset were tested, and more data were needed for evaluation in their studies.
For polyp detection in CTC, radiologists are usually interested in the polyps with diameter of 6 mm or larger and the voxel size of our CTC data is around 0.6 × 0.6 × 1 mm3. Therefore, a kernel with window size of 9 × 9 × 9, which covers the smallest polyp (6 mm) is selected in our existing CAD system20 for curvature estimation to reduce the possibility of those aforementioned thin structures occurs. This kernel size may not be further reduced since the reliable differentials of the image are required for curvature estimation.
Since the kernel size cannot be further reduced, we hypothesized that image upsampling by interpolation may solve the problem in an alternative way. In this paper, we present interpolation’s effect on curvature estimation for polyp detection in CTC. Our assumption is that upsampling the CT scan in each direction, while keeping the original kernel window size will reduce the risk of thin structures occurring within the kernel volume and will improve the performance of the kernel method, thereby leading to an improvement in polyp detection. Linear, quadratic B-spline, and cubic B-spline the three most commonly used techniques, are evaluated in this paper. We did not include other more computationally expensive interpolation methods because of their computational costs.
The paper is organized as follows. The kernel method for curvature computation and interpolation are described in Sec. 2. We demonstrate in Sec. 3. both visually and quantitatively the effectiveness of interpolation. Our concluding remarks are stated in Sec. 4. A preliminary version of this paper was presented at the MICCAI 2008 workshop.23
METHODS
Curvature
The curvature kt(p) of a point p in the tangent direction t on a surface can be directly computed from the partial derivatives17, 18 of the 3D gray value image as
| (1) |
where g is the gradient, and H is the Hessian matrix. There exist two mutual orthogonal tangent directions, for which the curvatures are external. They are called principal directions, with associated curvatures k1 and k2. Two classical measures of curvature at a point are the Gaussian curvature K=k1×k2 and mean curvature .
In this paper, the partial derivatives are estimated by the Deriche filters24 with the smoothing parameters α1 and α2. We set
| (2) |
Here, f0(x) is a smoothing operator, f1(x) a first-derivative operator, and f2(x) a second derivative operator. The coefficients c0, c1, c2, c3 are determined from the following normalizations within kernel window size M:
| (3) |
Given a 3D image I(x,y,z), the Gaussian curvature K and mean curvature H are computed as
| (4) |
| (5) |
where and the required partial derivatives are computed using, for example,
| (6) |
Finally, the principal curvatures of a surface at a point are given by
| (7) |
The selection of smoothing parameters α1 and α2 depends on different applications. For polyp detection, the optimal α1 = 0.7 and α2 = 0.1 are set as suggested in Ref. 20.
The polyp shape criterion
Curvature analysis can be used for polyp detection because of the uniqueness of curvature of colonic polyps with respect to the rest of the colonic surface. A normal colon consists of two primary surfaces: haustra and haustral folds. The haustra is concave and has elliptical pit curvature; the haustral folds have a saddle point curvature. However, a polyp is convex and thus has elliptical peak curvature. Thus, the basis of curvature-derived shape discriminators for polyp detection is going through each vertex on the colonic surface and tagging vertices that are classified as elliptical peaks (see Table TABLE I.).
TABLE I.
Curvature classification based on principal curvature values k1,2.
| Class | Shape | H | k1,2 | K |
|---|---|---|---|---|
| Elliptic | Pit | >0 | Same sign | >0 |
| Elliptic | Peak | <0 | Same sign | >0 |
| Hyperbolic | Saddle | Varies | Opposite sign | <0 |
Image resolution’s effect on curvature estimation
Image resolution has impact on the kernel method for curvature measurement. A continuous circle with radius r is used as an example. With baseline image resolution (voxel size without interpolation) set to h and interpolation factor f, a discrete circle with discrete radius results. For curvature measurement of a continuous arc of size Δθ rad, the corresponding discrete arc should consist of M discrete samples, where M is the kernel window size. M is related to Δθ and rd by
| (8) |
This shows that in general a larger window size M is required for a smaller voxel size. However, a kernel with a large window size will increase the possibility of encountering the aforementioned thin structures. In this paper, the voxel size h∕f should not be reduced by interpolating without limit since the window size M is fixed (9 × 9 × 9). Otherwise, the larger the interpolation factor that is applied, the less information is included in the kernel with fixed size M. The kernel approach will not produce reliable derivatives for curvature estimation. Therefore, without loss of generality, image interpolation by integer factors 2 and 4 are considered in our simulated data. For computational efficiency, interpolation by a factor of 2 is considered in our clinical CTC data.
B-spline interpolation
By using B-spline model, an interpolated value of f(x) at some coordinate x in a space of dimension q is defined as (Ref. 25)
where the ck is B-spline coefficients, and the basis function ϕ(x) is a tensor product of univariate B-splines of degree n
The univariate B-splines are defined as,
where is the one-sided power function
Given image array f(i), the coefficients ck can be determined by deconvolving such that the interpolated value f(x) fits the voxel values exactly: f(x)|x=i=f(i).
Degree n = 0: The B-spline of smallest degree n = 0 is almost identical to the nearest-neighbor interpolation.
Degree n = 1: The B-spline function β1 is also called linear interpolation.
Degree n = 2: The B-spline function β2 is also called quadratic B-spline interpolation.
Degree n = 3: The B-spline function β3 is also called cubic B-spline interpolation.
In this paper, linear, quadratic B-spline and cubic B-spline interpolations were implemented in ITK medical image processing library26 in a separable fashion (x, y and z interpolated independently) and were evaluated for curvature estimation.
CAD system with interpolation
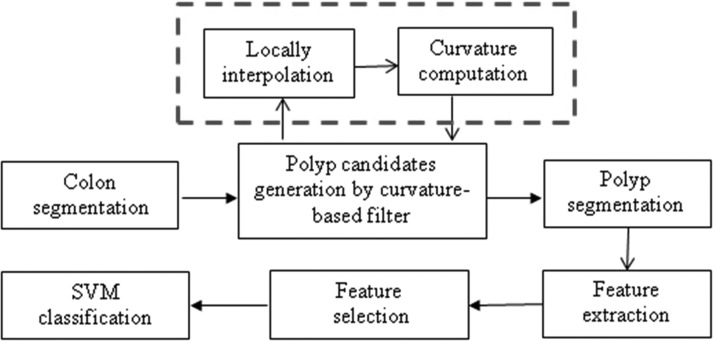
The main stages of our CAD system with interpolation (Fig. 1) include: (1) The colon is segmented by a region growing algorithm to identify the air- and contrast-filled colonic lumen7 (2) For each point on the segmented colon surface, we locally upsample the image by interpolation. The curvatures are analyzed and filtered based on Table TABLE I.. The filtered surface vertices are then clustered based on connectivity. The clusters are potential polyp candidates. (3) The centroid of each cluster is used as a seed for polyp candidate segmentation. (4) Characteristic features, such as intensity, shape and texture, are calculated from the segmented candidate. (5) The candidate pool is a large set, including true positive (TP) and false positive (FP) detections. Finally, a decision of true polyp or FP is made by a support vector machine (SVM) classifier.27 Note that only the subvolume around each voxel on the colon surface is interpolated for curvature analysis at the second stage, not the entire CTC image.
Figure 1.
Interpolation implemented in our CAD system.
Linear, quadratic B-spline and cubic B-spline25 interpolations were evaluated for the performance of polyp detection. The interpolation has been employed in the CAD scheme8 for polyp detection. However, our work is different with8 in two ways. First, in Ref. 8, linear interpolation was only applied to the adjacent slices (z) to get isotropic volume. We upsample the sub image by three interpolation methods in x, y, and z directions. Second, the entire axial CTC image was interpolated at the first step for further analysis in Ref. 8, while our method locally upsamples the sub image (a small image around each voxel on the colon surface) by interpolation for curvature estimation.
RESULTS
In this section, the performance of interpolation is assessed on both simulated images as well as clinical CTC data.
Single sphere simulation
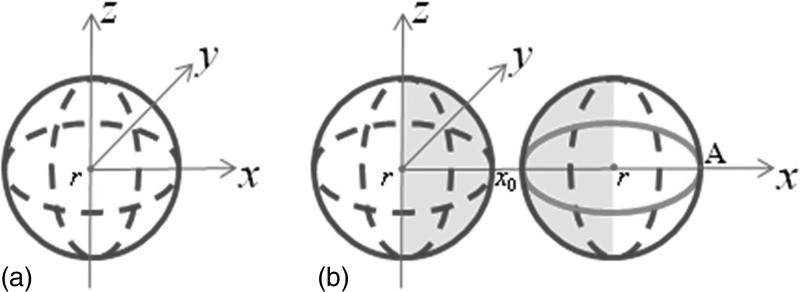
A sphere [Fig. 2a] with a radius of r = 0.5 is given by the parameterization (rcosusinv,rsinusinv,rcosv), u∈[0,2π],v∈[0,π]. The initial image intensity of the sphere is 100, and voxel size is 0.1 × 0.1 × 0.1. Gaussian kernel at σ = 3 is applied to smooth the initial image. This sphere with a digital radius rd=5 voxels (rd=r∕0.1) simulated a 6 mm polyp in diameter because voxel size of CTC is around 0.6 × 0.6 × 1 mm3 and a 6 mm polyp roughly occupies ten voxels in x and y directions.
Figure 2.
Sphere simulation. (a) A sphere with a radius of r = 0.5, which is comparable to a 6 mm polyp. Curvatures of all surface points are examined. (b) A pair of spheres with a radius of 0.5. Curvatures of the surface points close to each other (highlighted regions) are examined.
For evaluation of estimation quality, curvature error Ek (Ref. 28) is defined as
| (9) |
where is the curvature estimated at voxel c, and ρ(c) is the probability density function. Curvature error Ek is an average over all points on surface S, specified as a fraction of the squared true curvature kt.
Ek is composed of two parts. The curvature bias, Bk, expresses the accuracy in analogy with the bias known from measurements in physics.
| (10) |
The second component of the curvature error is the curvature deviation Sk, quantifying the precision of a curvature estimation method.
| (11) |
where denotes the estimated curvature averaged over all voxels on surface S.
The bias and deviation relate to the curvature error as
| (12) |
Gaussian curvature and mean curvature are computed by Eqs. 4, 5 for all points on the sphere surface. The kernel window size is 9 × 9 × 9, which is roughly equal to the sphere size. The true values are k1=k2=1∕r=2, K=4, and H=2. Too much upsampling will cause more blurring, therefore interpolation by an integer factor 2 and 4 are evaluated. Gaussian curvature error EK, bias BK, deviation SK, mean curvature error EH, bias BH, and deviation SH with and without interpolation are summarized in Table TABLE II.. We found that: (1) curvature errors are dramatically reduced with interpolation and are similar for different interpolation factors. (2) Curvature bias is reduced with interpolation and further reduced with higher interpolation factor. (3) Curvature deviations are the same or slightly increased with interpolation. (4) The performances are similar for all three interpolation methods.
TABLE II.
Mean curvature error EH, bias BH, and deviation SH and Gaussian curvature error EK, bias BK, and deviation SK on the sphere surface, with and without interpolations. Subscript 2 and 4 corresponds to interpolation by a factor of 2 or 4, respectively.
| None (%) | Linear2 (%) | Quadratic2 (%) | Cubic2 (%) | Linear4 (%) | Quadratic4 (%) | Cubic4 (%) | |
|---|---|---|---|---|---|---|---|
| EH | 0.5 | 0.36 | 0.36 | 0.36 | 0.37 | 0.37 | 0.37 |
| BH | 4.28 | 1.89 | 1.90 | 1.90 | 0.67 | 0.68 | 0.68 |
| SH | 5.65 | 5.72 | 5.71 | 5.71 | 6.09 | 6.01 | 6.02 |
| EK | 2.24 | 1.55 | 1.55 | 1.55 | 1.55 | 1.52 | 1.52 |
| BK | 9.06 | 4.13 | 4.15 | 4.16 | 1.68 | 1.71 | 1.71 |
| SK | 11.91 | 11.75 | 11.72 | 11.72 | 12.34 | 12.20 | 12.22 |
Double sphere simulation
To directly address the issue of adjacent surface interference,such as polyps that lie on or near haustral folds, a second spherewith a radius of r = 0.5 [Fig. 2b] is placed close to the first sphere in Fig. 2a. This assures that when the kernel is placed at the edge points that are closest to each other, the kernel will contain both spheres. Once again, Gaussian smoothing with σ = 3 was applied and curvatures of points on the surface close to each other [highlighted regions in Fig.2b] are examined with and without interpolations. Gaussian curvature error EK, bias BK, deviation SK and mean curvature error EH, bias BH, deviation SH with and without interpolation are summarized in Table TABLE III.. The results are similar to those from the one sphere experiments except that the curvature deviations are also reduced with interpolations.
TABLE III.
Mean curvature error EH, bias BH, and deviation SH and Gaussian curvature error EK, bias BK, and deviation SK on double spheres measured on the highlighted regions in Fig. 2b, with and without interpolation.
| None (%) | Linear2 (%) | Quadratic2 (%) | Cubic2 (%) | Linear4 (%) | Quadratic4 (%) | Cubic4 (%) | |
|---|---|---|---|---|---|---|---|
| EH | 1.17 | 0.42 | 0.41 | 0.41 | 0.39 | 0.37 | 0.37 |
| BH | 4.44 | 1.52 | 1.54 | 1.55 | 0.37 | 0.39 | 0.39 |
| SH | 9.86 | 6.31 | 6.23 | 6.22 | 6.24 | 6.10 | 6.10 |
| EK | 5.71 | 1.79 | 1.75 | 1.74 | 1.6 | 1.53 | 1.53 |
| BK | 9.34 | 3.38 | 3.43 | 3.43 | 1.06 | 1.10 | 1.09 |
| SK | 21.99 | 12.95 | 12.77 | 12.75 | 12.60 | 12.33 | 12.32 |
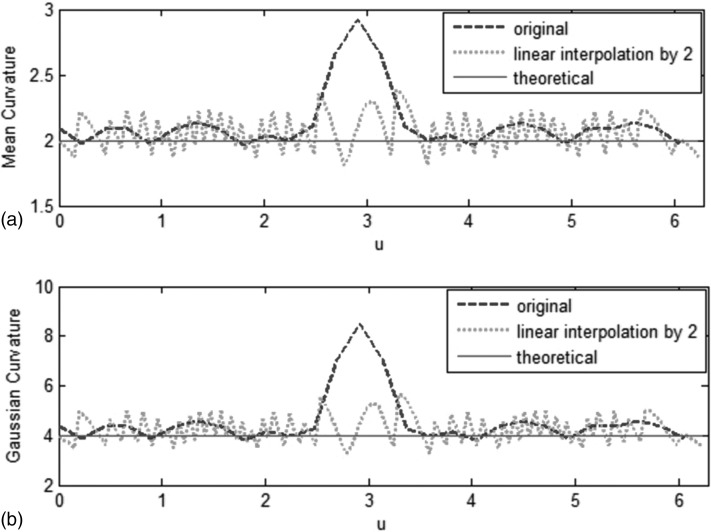
Figure 3 shows plots of themean and Gaussian curvatures along the points in thexy-plane as a function of u. [Fig. 2b shows the path ofplotsstarting at the point labeled A.] For the two spheres, kernel method without interpolation causes a large error in the mean and Gaussian curvature estimates at the location closest to the additional sphere, corresponding to the spikes in Figs. 3a, 3b. However, curvature estimation with linear interpolation by a factor of 2 is more accurate.
Figure 3.
Comparison of mean curvatures (a) and Gaussian curvature (b) in xy-plane as a function of u∈[0,2π]. Kernel method without interpolation causes a large error in mean curvature [spike in (a)] and Gaussian curvature [spike in (b)] at the location closest to the additional sphere. Curvature estimation with linear interpolation by a factor of 2 is more accurate.
Large clinical data set
For quantitative evaluation, the performance of interpolation’s effect on polyp detection in CTC is evaluated on CT scans of 1186 patients. The use of this patient data was approved by our institution’s Office of Human Subjects Research. Every patient was scanned twice—once supine and once prone. Each scan was done during a single breath hold using a four-channel or eight-channel CT scanner (General Electric Light Speed or Light Speed Ultra, GE Healthcare Technologies, Waukesha, WI). CT scanning parameters included 1.25–2.5 mm section collimation, 15 mm table speed, 1 mm reconstruction interval, 100 mAs, and 120 kVp.
These scans are divided into a training set (containing 395 patients) and a test set (containing 791 patients). There are 108 and 267 colonoscopy-confirmed polyps measuring 6–9 mm in the training set and test set, respectively. Since current detection algorithms perform very well on polyps 10 mm or larger,2 and small polyps are more likely to have errors in curvatures as we described earlier, we focus on the detection of 6–9 mm polyps. To some extent, improving the detection probability of 6–9 mm polyps is the main target of current CTC CAD research.
The simulated sphere results show similar performance for interpolation by a factor of 2 and 4. For computational efficiency, linear, quadratic B-spline, and cubic B-spline interpolations by a factor of 2 are evaluated on the large clinical CTC data. In the training stage, colon segmentation, identification of suspected polyps, and polyp segmentation are applied to the training data. After that, quantitative features are then computed for each suspected polyp. A progressive feature selection is run on all patients in the training set to select three pertinent features for one SVM. Then a committee optimization process is performed to form a committee of seven SVMs.27 In the test stage, for any given data, the detections and features are fed into the SVM committee and confidence level for each detection, SVM vote, are then determined for classification. By plotting the true positive fraction (TPF) against the false positive fraction (FPF) at the different SVM votes, a free response receiving operation characteristic (FROC) curve is obtained.
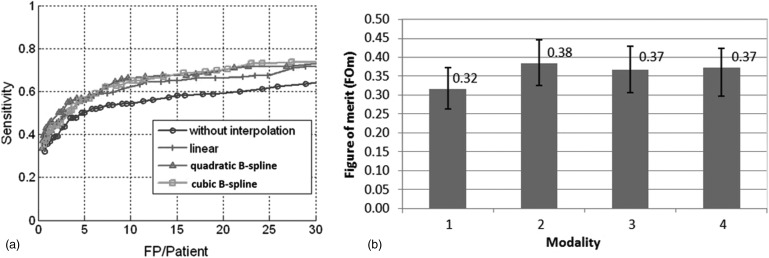
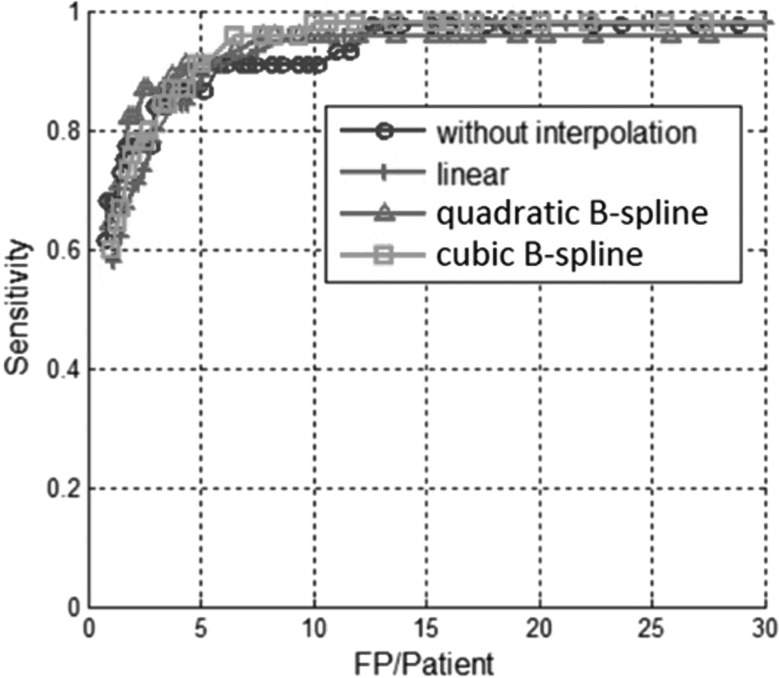
The FROC curves with and without interpolations on the 6–9 mm polyps on test data (containing 267 polyps) are compared [Fig. 4a]. Our CAD system withoutinterpolation successfully detected 190 out of 267 polyps with 147 false positives per patient before classification. The SVM classifier achieved 55% (146 out of 267) sensitivity at ten false positives per patient (93% reduction). The CAD system with linear interpolation by two detected 217 out of 267 polyps with 220 false positives per patient at the initial stage. The SVM classifier achieved 62% (165 out of 267) sensitivity at 10 FP per patient (95% reduction). The sensitivities with interpolation are increased by 7%–11% at a rate of ten false positive detections per patient. More quantitative results are summarized in Table TABLE IV..
Figure 4.
(a) FROC curves for 6–9 mm polyps on test data which show no interpolation and three interpolations. The curves show the benefits of the interpolation for small polyps. (b) jafroc FOM for different modalities. (modalities 1–4 represent CAD without interpolation, CAD with linear, quadratic B-spline and cubic B-spline interpolation, respectively.) Error bars present 95% confidence intervals.
TABLE IV.
Comparing sensitivities at 10 FP per patient for CAD without and with interpolations for 6–9 mm polyps on test data.
| CAD w∕o Interpolation | CAD with linear Interpolation | CAD with quadratic B-spline Interpolation | CAD with Cubic B-spline Interpolation | |
|---|---|---|---|---|
| Sensitivity | 55%(146∕267) | 62%(165∕267) | 66%(176∕267) | 65%(174∕267) |
The FROC data are analyzed by using the jackknife FROC(jafroc),29 implemented in the software jafroc version 2.3.30jafroc computes a figure of merit (FOM), which is defined as the probability that a true lesion rating exceeds all false lesion rating in a normal case. The computation of FOM is identical to calculation of the Wilcoxon test statistic for two samples.31 Figure 4b shows the FOM of all four modalities (CAD without interpolation, linear, quadratic B-spline, and cubic B-spline interpolation) and the intermodality difference between FOMs with 95% confidence intervals are summarized in Table TABLE V.. We found that CAD with any of the methods of interpolation significantly improved the sensitivity of polyp detection. There is no significant difference among the three methods.
TABLE V.
Intermodality differences and 95% confidence intervals of jafroc FOM. If the 95% CI does not include 0, then the corresponding modality pairs are significantly different.
| Inter-Modality | Difference of FOM and 95% CI |
|---|---|
| None and Linear | −0.069(−0.119,−0.018)a |
| None and Quadratic B-spline | −0.051(−0.101,−0.001)a |
| None and Cubic B-spline | −0.050(−0.100,−0.002)a |
| Linear and Quadratic B-spline | 0.018(−0.032,0.068) |
| Linear and Cubic B-spline | 0.017(−0.027,0.053) |
| Quadratic B-spline and Cubic B-spline | 0.007(−0.035,0.070) |
Significantly different.
Two examples of polyps missed by CAD without interpolation but found with cubic B-spline interpolation are shown in Fig. 5. The interpolation benefits the small polyps, at the same time, the FROC curves with and without interpolations on the 10 mm or larger polyps (Fig. 6) show that the interpolations do not affect the performance for large polyps.
Figure 5.
Polyps missed without interpolation but found with cubic B-spline interpolation at 10 FP per patient: (a) an 8 mm ademoma in sigmoid colon and (b) a 6 mm adenoma in sigmoid colon .
Figure 6.
FROC curves for 10 mm or larger polyps which show CAD performance with and without interpolation on test data. Three different interpolation methods are shown (linear, quadratic B-spline, cubic B-spline). Unlike the situation for detecting the small polyps, the curves show that interpolation does not significantly affect the performance of CAD for detecting large polyps.
DISCUSSION
In this paper, we were focusing on the kernel method for curvature estimation and the goal of this paper was to present the interpolations’ effect on curvature estimation in computer-aided diagnosis of polyp in CTC. In this specific application, surface curvatures are important geometric features. However, the general kernel approach for curvature computation could yield erroneous results for thin structures such as folds in the colon wall, for small (6–9 mm) polyps, and for polyps that lie on haustral folds. Those erroneous curvatures will reduce the performance of polyp detection. This paper compares three commonly used interpolation techniques’ effect on curvature estimation, including linear, quadratic B-spline, and cubic B-spline interpolations. The utility of improved curvature estimates were confirmed by the CAD results, where the use of interpolation led to an increase in the standalone sensitivity of the CAD system for detecting 6–9 mm polyps of 7%–10% at ten FP per patient on a large screening population. This improved CAD performance demonstrates that this incremental improvement in the curvature estimate can have a substantial impact on CTC-CAD performance.
Since curvature is computed from the partial derivatives of gray-scale images [Eq. 1], the fundamental reason interpolation can improve curvature accuracy is because the estimation accuracy of partial derivatives is improved by interpolation. Similar to our work, Oda et al.32 proposed a method to improve the accuracy of partial derivatives by interpolating intensity by curve fitting and applied it for polyp detection. A quadratic polynomial curve was fitted to the neighborhood of each voxel in the colonic wall for better estimation of the Hessian matrix. Then, a detection response was computed based on the eigenvalues of the Hessian matrix for polyp detection.
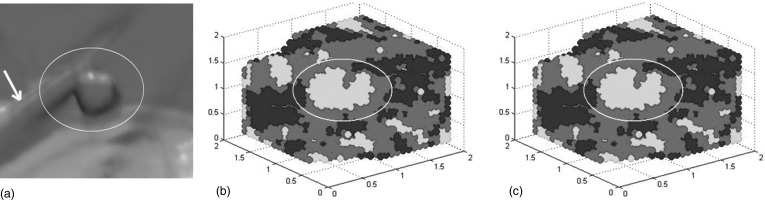
An unintended negative effect of interpolating is the increase in the number of false lesions that are detected.We ran our CAD system on one illustrative case (one of the clinical data described in Sec. 3C) and the estimated curvatures around one polyp are shown in Fig. 7. All vertices on a given iso-surface were classified according to their curvature type (Table TABLE I.), where elliptical peak (potential polyp) was represented by bright regions, elliptical pit (potential haustral) by dark regions and saddle (potential haustral fold) by grey regions. We can see that for the polyp next to a fold [Fig. 7a], the detected lesion area inaccurately leaks onto the fold [Fig. 7b] when no interpolation is applied. However, when cubic B-spline interpolation is applied, the lesion is accurately separated from the fold [Fig. 7c]. This example demonstrates one of the problem situations described earlier (polyp next to fold) and how interpolation correctly isolates the polyp. At the same time, the increased number of false lesions is seen by comparing Figs. 7b, 7c.
Figure 7.
Clinical data example with a polyp present (a). Curvature classification without (b) and with cubic B-spline interpolation (c). Potential lesions are represented by bright regions. A normal colonic fold that abuts the polyp is indicated with an arrow in (a).
Quantitatively, for example, for the test set, which has 267colonoscopy-confirmed polyps in 6–9 mm, our original CAD system successfully detected 190 out of 267 polyps at a rate of 147 false positives per patient at the initial stage. The SVM classifier achieved 55% (146 out of 267) sensitivity at ten false positives per patient (93% reduction). The CAD system with linear interpolation by a factor of 2 detected 217 out of 267 polyps at a rate of 220 false positives per patient initially. The SVM classifier achieved 62% (165 out of 267) sensitivity at ten false positives per patient (95% reduction). Our results (Fig. 4 and Table TABLE IV.) show that those additional false detections are discarded in the classification step and do not reduce the performance of our CAD system. This is mainly because those features (such as mean curvature, Gaussian curvature, aspect ratio, compactness, and curvedness) selected for the SVM classifier are curvature-related and thus interpolation lead to a better classification.
Image resolution affects kernel-based curvature estimation. According to Eq. 8, a kernel with a larger window size is chosen for smaller image resolution. However, a larger kernel window will increase the possibility of encountering thin structures. In this paper, since the smallest target polyp size is 6 mm, and the voxel size of CTC is around 0.6 × 0.6 × 1 mm3, we set the kernel to 9 × 9 × 9 to cover the smallest polyp. The image should not be upsampled extremely since the window size is fixed. The more the image is upsampled, the less information is included in the kernel. The kernel approach will not get reliable derivatives for curvature estimation. Therefore, interpolation by a factor of 2 is considered in our CTC data.
Recent advances in CTC improved CAD performance with higher sensitivity in many ways. Scatter correction33, 34 was used in image preprocessing to reduce pseudo-enhancement phenomenon introduced by high-density orally administered contrast agents in fecal-tagging CTC and the method achieved an 8% improvement for detecting polyps 6–9 mm in size. A new dimensionality reduction classifier, diffusion map and local linear embedding (DMLLE),35 was developed for false positives reduction and yielded a 10% improvement for 6–9 mm polyps. Konukoglu36 proposed polyp enhancing level sets method to improve the performance of CTC CAD algorithms, especially for smaller polyps. CAD performance increased 5%–10% when higher quality CTC data was tested.37 In addition, electronic cleansing,38 logistic regression,39 massive-training artificial neural network (MTANN),40 supine-prone correspondence,41 and feature-guided analysis42 have been utilized to improve CAD performance by false positive reduction. While each improvement alone increases sensitivity only a small amount, it is possible to get a clinically useful CAD system with high performance if all of these efforts are combined.
Polyps in 6–9 mm size range are important for guidingpatient care and some investigators believe patients with such polypscan be placed into a surveillance population rather than undergo immediate polypectomy. Patients in the surveillance population would undergo more frequent CTC evaluation than those returning to the screening population. Such polyps are harder to detect for both radiologists and CAD system. Other studies43, 44 have achieved sensitivities and false positive rates comparable with those we report (Table TABLE IV.).
In summary, this paper presents the interpolations’ effect on curvature estimation in computer-aided diagnosis of polyp in CTC. We conclude from both simulated data and real data that any one of the three interpolations significantly improved the sensitivity of CAD for polyp detection in CTC. Although there were no significant differences among those three interpolations, quadratic B-spline or cubic B-spline is preferred in our application.
ACKNOWLEDGMENTS
This research was supported by the Intramural Research Program of the NIH Clinical Center. We thank Dr. Perry Pickhardt, Dr. J. Richard Choi, and Dr. William Schindler for providing CT colonography data.
Presented in part at the 2008 MICCAI Workshop: Computational and Visualization Challenges in the New Era of Virtual Colonoscopy, New York.
References
- Muto T., Bussey H. J., and Morson B. C., “The evolution of cancer of the colon and rectum” Cancer, 36(6), 2251–2270 (1975). 10.1002/cncr.2820360944 [DOI] [PubMed] [Google Scholar]
- Summers R. M. et al. , “Computed tomographic virtual colonoscopy computer-aided polyp detection in a screening population,” Gastroenterology, 129(6), 1832–1844 (2005). 10.1053/j.gastro.2005.08.054 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Summers R. M. and Yoshida H., Future Directions: Computer-Aided Diagnosis, in Atlas of Virtual Colonoscopy, Dachman A. H., Editor (Springer, New York, 2003) pp. 55–62. [Google Scholar]
- Vining D. J., Ge Y., Ahn D. K., and Stelts D. R., “Virtual colonoscopy with computer-assisted polyp detection,” in Computer-Aided Diagnosis in Medical Imaging,” Proceedings of the First International Workshop on Computer-Aided Diagnosis, edited by Doi K., MacMahon H., Giger M. L., and Hoffmann K. R. (Elsevier, Chicago, 1999), pp. 445–452.
- Paik D. S., Beaulieu C. F., Jeffrey R. B., Yee J., Steinauer-Gebauer A. M., and Napel S., “Computer aided detection of polyps in CT colonography: Method and free-response ROC evaluation of performance,” Radiology, 217–370 (2000). 10644127
- Paik D. S. et al. , “Surface normal overlap: A computer-aided detection algorithm, with application to colonic polyps and lung nodules in helical CT,” IEEE Trans. Med. Imaging, 23(6), 661–675 (2004). 10.1109/TMI.2004.826362 [DOI] [PubMed] [Google Scholar]
- Summers R. M. et al. , “Automated polyp detection at CT colonography: Feasibility assessment in a human population,” Radiology, 219(1), 51–59 (2001). [DOI] [PubMed] [Google Scholar]
- Yoshida H. and Nappi J., “Three-dimensional computer-aided diagnosis scheme for detection of colonic polyps,” IEEE Trans. Med. Imaging, 20(12), 1261–1274 (2001). 10.1109/42.974921 [DOI] [PubMed] [Google Scholar]
- Gokturk S. B. et al. , “A statistical 3-D pattern processing method for computer-aided detection of polyps in CT colonography,” IEEE Trans. Med. Imaging, 20(12), 1251–1260 (2001). 10.1109/42.974920 [DOI] [PubMed] [Google Scholar]
- Acar B. et al. , “Edge displacement field-based classification for improved detection of polyps in CT colonography,” IEEE Trans. Med. Imaging, 21(12), 1461–1467 (2002). 10.1109/TMI.2002.806405 [DOI] [PubMed] [Google Scholar]
- Kiss G. et al. , “Computer-aided diagnosis in virtual colonography via combination of surface normal and sphere fitting methods,” Eur. Radiol. 12(1), 77–81 (2002). 10.1007/s003300101040 [DOI] [PubMed] [Google Scholar]
- Wang S. et al. , “Volume-based Feature Analysis of Mucosa for Automatic Initial Polyp Detection in Virtual Colonoscopy,” Int. J. Comput. Assist. Radiol. Surg. 3(1-2), 131–142 (2008). 10.1007/s11548-008-0215-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor S. A. et al. , “Computer-aided detection for CT colonography: Incremental benefit of observer training. Br J Radiol,” 81(963), 180–186 (2008). 10.1259/bjr/93375459 [DOI] [PubMed] [Google Scholar]
- Kitasaka T. et al. , “A method for detecting colonic polyps using curve fitting from 3D abdominal CT images,” Proc. SPIE Med. Imaging, 5746, 403–414 (2005). [Google Scholar]
- Sander P. T. and Zucker S. W., “Inferring Surface Trace and Differential Structure from 3-D Images,” IEEE Trans. PAMI, 12(9), 833–854 (1990). 10.1109/34.57680 [DOI] [Google Scholar]
- Sundaram P. et al. , “Colon polyp detection using smoothed shape operators: Preliminary results,” Med. Image Analysis, 12, 99–119 (2008). 10.1016/j.media.2007.08.001 [DOI] [PubMed] [Google Scholar]
- Monga O. and Benayoun S., “Using partial derivatives of 3D images to extract typical surface features,” Comput. Vis. Image Underst. 61(2), 171–189 (1995). 10.1006/cviu.1995.1014 [DOI] [Google Scholar]
- Thirion J.-P. and Gourdon A., “Computing the differential characteristics of isointensity surfaces,” Comput. Vis. Image Underst. 61(2), 190–202 (1995). 10.1006/cviu.1995.1015 [DOI] [Google Scholar]
- Zhu H., Fan Y., and Liang Z., “Improved curvature estimation for shape analysis in computer-aided detection of colonic polyps,” in Proceedings of MICCAI 2010 Workshop: Virtual Colonoscopy and Abdominal Imaging, Beijing, China, September 20-24, 2010.
- Campbell S. R. and Summers R. M., “Analysis of Kernel Method for Surface Curvature Estimation in CARS 2004 - Computer Assisted Radiology and Surgery,” Proceedings of the 18th International Congress and Exhibition, Chicago, USA, June 23-26, 2004.
- Wijk C.v.et al. , “On normalized convolution to measure curvature features for automatic polyp detection,” MICCAI 2004. LNCS 3216, pp. 200–208.
- Zhu H.et al. , “Computer-aided detection of colonic polyps with level set-based adaptive convolution in volumetric mucosa to advance CT colonography toward a screening modality,” Cancer Manage. Res. 1–13 (2009). [DOI] [PMC free article] [PubMed]
- Liu J.et al. , “Colon Cancer Polyp Detection: Calculating Curvature Using Deriche Filters and Interpolation,” Proceedings of the MICCAI 2008 Workshop: Computational and Visualization Challenges in the New Era of Virtual Colonoscopy, New York, September, 2008, pp. 40–45.
- Deriche R., “Recursively implementing the Gaussian and its derivatives,” in the Proceedings of the Second Singapore InernationalConference on Image Processing, edited by Srihivasan V., Sim Heng O., and Yew Hock A., September 1992, pp. 263–267.
- Thevenaz P., Blu T., and Unser M., “Interpolation revisited,” IEEE Trans. Med. Imaging, 19(7), 739–758 (2000). 10.1109/42.875199 [DOI] [PubMed] [Google Scholar]
- NLM Insight Segmentation and Registration Toolkit. 2004, Available from: http://www.itk.org.
- Yao J., Summers R. M., and Hara A. K., “Optimizing the committee of support vector machines (SVM) in a colonic polyp CAD system,” Med. Imaging, 5746, 384–392 (2005). [Google Scholar]
- Worring M. and Smeulders A. W. M., “Digital curvature estimation,” CVGIP Image Understand. 58(3), 366–382 (1993). 10.1006/ciun.1993.1048 [DOI] [Google Scholar]
- Chakraborty D. P. and Berbaum K. S., “Observer studies involving detection and localization: modeling, analysis, and validation,” Med. Phys. 31(8), 2313–2330 (2004). 10.1118/1.1769352 [DOI] [PubMed] [Google Scholar]
- Chakraborty D. P., “Analysis of location specific observer performance data: Validated extensions of the jackknife free-response (JAFROC) method,” Acad. Radiol. 13(10), 1187–1193 (2006). 10.1016/j.acra.2006.06.016 [DOI] [PubMed] [Google Scholar]
- Ruschin M. et al. , “Dose dependence of mass and microcalcification detection in digital mammography: free response human observer studies,” Med. Phys. 34(2), 400–407 (2007). 10.1118/1.2405324 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oda M. et al. , “Digital bowel cleansing free colonic polyp detection method for fecal tagging CT colonography,” Acad. Radiol. 16(4), 486–494 (2009). 10.1016/j.acra.2008.10.011 [DOI] [PubMed] [Google Scholar]
- Liu J., Yao J., and Summers R., “Scale-based scatter correction for computer-aided polyp detection in CT colonography,” Med. Phys. 35(12), 5664–5671 (2008). 10.1118/1.3013552 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nappi J. and Yoshida H., “Adaptive correction of the pseudo-enhancement of CT attenuation for fecal-tagging CT colonography,” Med. Image Analysis, 12(4), 413–426 (2008). 10.1016/j.media.2008.01.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang S., Yao J., and Summers R., “Improved classifier for computer-aided polyp detection in CT colonography by nonlinear dimensionality reduction,” Med. Phys. 35(4), 377–386 (2008). 10.1118/1.2820900 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Konukoglu E. et al. , “Polyp enhancing level set evolution of colon wall: method and pilot study,” IEEE Trans. Med. Imaging, 26(12), 1649–1656 (2007). 10.1109/TMI.2007.901429 [DOI] [PubMed] [Google Scholar]
- Summers R. M. et al. , “Performance of a Previously Validated CT Colonography CAD System on a New Patient Population,” AJR Am. J. Roentgenol, 191, 168–174 (2008). 10.2214/AJR.07.3354 [DOI] [PubMed] [Google Scholar]
- Cai W., Zalis M., and Yoshida H., “Reduction of Electronic-cleansing Artifacts in Cathartic and Non-cathartic Fecal-tagging CT Colonography,” Proceedings of the MICCAI 2008 Workshop: Computational and Visualization Challenges in the New Era of Virtual Colonoscopy, New York, September 2008, pp. 70–77.
- van Ravesteijn V. F., et al. , “Computer Aided Detection of Polyps in CT Colonography Using Logistic Regression,” IEEE Trans. Med. Imaging, 29, 120–131 (2010). 10.1109/TMI.2009.2028576 [DOI] [PubMed] [Google Scholar]
- Suzuki K. et al. , “Massive-training artificial neural network (MTANN) for reduction of false positives in computer-aided detection of polyps: Suppression of rectal tubes,” Med. Phys. 33(10), 3814–3824 (2006). 10.1118/1.2349839 [DOI] [PubMed] [Google Scholar]
- Nappi J. et al. , “Region-based supine-prone correspondence for the reduction of false-positive CAD polyp candidates in CT colonography,” Acad. Radiol. 12(6), 695–707 (2005). 10.1016/j.acra.2004.12.026 [DOI] [PubMed] [Google Scholar]
- Nappi J. and Yoshida H., “Feature-guided analysis for reduction of false positives in CAD of polyps for computed tomographic colonography,” Med. Phys. 30(7), 1592–1601 (2003). 10.1118/1.1576393 [DOI] [PubMed] [Google Scholar]
- Bogoni L. et al. , “Computer-aided detection (CAD) for CT colonography: a tool to address a growing need,” Br J. Radiol. 78(spec. 1) S57–S62 (2005). 10.1259/bjr/25777270 [DOI] [PubMed] [Google Scholar]
- Taylor S. A. et al. , “Computer-assisted reader software versus expert reviewers for polyp detection on CT colonography,” AJR Am. J. Roentgenol 186(3), 696–702 (2006). 10.2214/AJR.04.1990 [DOI] [PubMed] [Google Scholar]