AMASS: Algorithm for MSI Analysis by Semi-supervised Segmentation

Abstract

Mass Spectrometric Imaging (MSI) is a molecular imaging technique that allows the generation of 2D ion density maps for a large complement of the active molecules present in cells and sectioned tissues. Automatic segmentation of such maps according to patterns of co-expression of individual molecules can be used for discovery of novel molecular signatures (molecules that are specifically expressed in particular spatial regions). However, current segmentation techniques are biased towards the discovery of higher abundance molecules and large segments; they allow limited opportunity for user interaction and validation is usually performed by similarity to known anatomical features.

We describe here a novel method, AMASS (Algorithm for MSI Analysis by Semi-supervised Segmentation). AMASS relies on the discriminating power of a molecular signal instead of its intensity as a key feature, uses an internal consistency measure for validation, and allows significant user interaction and supervision as options. An automated segmentation of entire leech embryo data images resulted in segmentation domains congruent with many known organs, including heart, CNS ganglia, nephridia, nephridiopores, and lateral and ventral regions, each with a distinct molecular signature. Likewise, segmentation of a rat brain MSI slice data set yielded known brain features, and provided interesting examples of co-expression between distinct brain regions. AMASS represents a new approach for the discovery of peptide masses with distinct spatial features of expression.

1 Introduction

The use of multiple imaging techniques to assess the presence and location of specific proteins in tissues and cells is central to the study of biological systems. Historically, successful approaches usually involved labeling one/few proteins at a time either by attaching a fluorescent domain genetically or by treating a biological sample with labeled antibodies, and then recording two-dimensional (2D) micrographs of the sample, possibly also reconstructing them into a three-dimensional (3D) object or movie. Such imaging techniques are low-to-medium throughput approaches and give the biologist insight into just a small number of biological samples, limited to known proteins for which antibodies or tagged forms are available. By contrast, there is an increasing number of imaging technologies (transcriptomic or proteomic) that allow for the sampling and exploration of the entire complement of active molecules in the cell.

Mass Spectrometric Imaging (MSI) is a molecular imaging technique which allows the generation of 2D ion density maps for a large complement of the molecules present in the tissue under study¹. In the Matrix-Assisted Laser Desorption/Ionization (MALDI) MSI workflow, thin tissue sections (10 – 15µm) from organs, or even whole dissected specimens, are mounted onto a transparent glass slide, allowing microscopic observation of the material prior to MS analysis. After deposition of the MALDI matrix, automated direct MALDI analysis of tissue sections provides information on masses of the desorbed molecules in a 2D raster defined by the selected positions of the laser beam². The studies performed by various groups^3–7 have demonstrated that acquisition of tissue expression profiles while maintaining cellular and molecular integrity is feasible. With automation and new analysis software, it has also become possible to produce multiplex imaging maps of selected bio-molecules within tissue sections^1,2,8. Molecules that are preferentially expressed in a region of the sample will show higher intensities in that region when looking at the image corresponding to the specific m/z value associated with the molecule. Discovery of these molecules often involved observing the images for each mass value sequentially in a movie, to short-list ones with interesting patterns.

Most bioinformatics approaches have focused on making the discovery process easier by allowing computational queries of MSI data-sets. In previous work⁹, we started with a supervised approach in which we assumed that the region of interest (ROI) is specified based on pre-selected morphological criteria. As an example of an ROI, consider the central nervous system (CNS) of the medicinal leech, Hirudo medicinalis, one of the best-studied representatives of the phylum Annelida (segmented worms). Given a particular ROI, we asked if (a) there were specific molecular signatures or collections of peptide mass values that are specific to the ROI; and, (b) which peptides correspond to these masses. We identified molecular signatures for many ROIs, including 43 m/z values in the CNS, and identified 35 peptides, one of which was a novel member of the intermediate filament family (which we named HmIF4), which appears to be involved in neural development.

By contrast, unsupervised approaches (no pre-specified ROI) seek to computationally segment (or partition) MALDI spots into regions, each characterized by a specific molecular signatures or profile. In most cases, the idea is to treat each MALDI spot as a vector of expressed masses, and to apply unsupervised clustering techniques for segmentation. Principal Component Analysis (PCA) and hierarchical clustering (HC) are classic non-parametric clustering techniques, and have been used successfully for MSI^10–13. Alexandrov et al. argue that these methods do not take advantage of the spatial clustering of MSI spots and develop a technique based on edge detection and smoothing¹¹. While these clustering-based methods show promising results, they need to be optimized both in memory and runtime to be able to process the full MSI datasets which are typically large. For example a data set acquired on 20000 MALDI spots with 40000 m/z values for each spectrum yields a dataset of 800 million values (3.2GB). Typically, MSI datasets are reduced for processing by decreasing mass resolution^10,15, by applying a discrete wavelet transform¹⁶ to each spectrum, or by explicit peak selection on each spectrum^14,15. Normally, the peak-picking is performed at a pre-processing stage in a spectrum-wide manner based only on the intensity and the shape of a potential peak. If a region of interest is characterized by a single (or a few) peaks that are not among the most intense peaks in a region, these peaks may be omitted during peak-picking, making the region indistinguishable from others. The standard clustering approaches also does not rely on any a priori knowledge about tissue morphology. Finally, unsupervised clustering-based segmentation methods are useful but limited in providing a user an opportunity to go deeper into the data analysis. Most significantly, we find in our investigations that segments overlap because they share peaks so it is important to allow the user to make a reasoned choice.

In this paper, we address these issues explicitly. We start with the difficult question of what constitutes a `good' segmentation. Prevailing methods implicitly equate good segmentation to ones that match known morphological features of tissues observed through optical methods^10,12,14. While this validation is natural and provides direct visual feedback – indeed we use it as one technique in this report (see Figures 4 and 5) – it has problems. Often, molecules are expressed in multiple, morphologically distinct, regions. Segmenting images so as to conform to known morphology will inhibit the discovery of novel molecular signatures. Second, MSI resolution (20–70 µm) is still inferior to optical resolution (< 1 µm). The potential of MSI is not as a replacement of optical methods, but to help identify the molecular basis of morphological differentiation. Therefore, we judge image-segmentation quality with alternative criteria based on molecular signatures.

Figure 4.

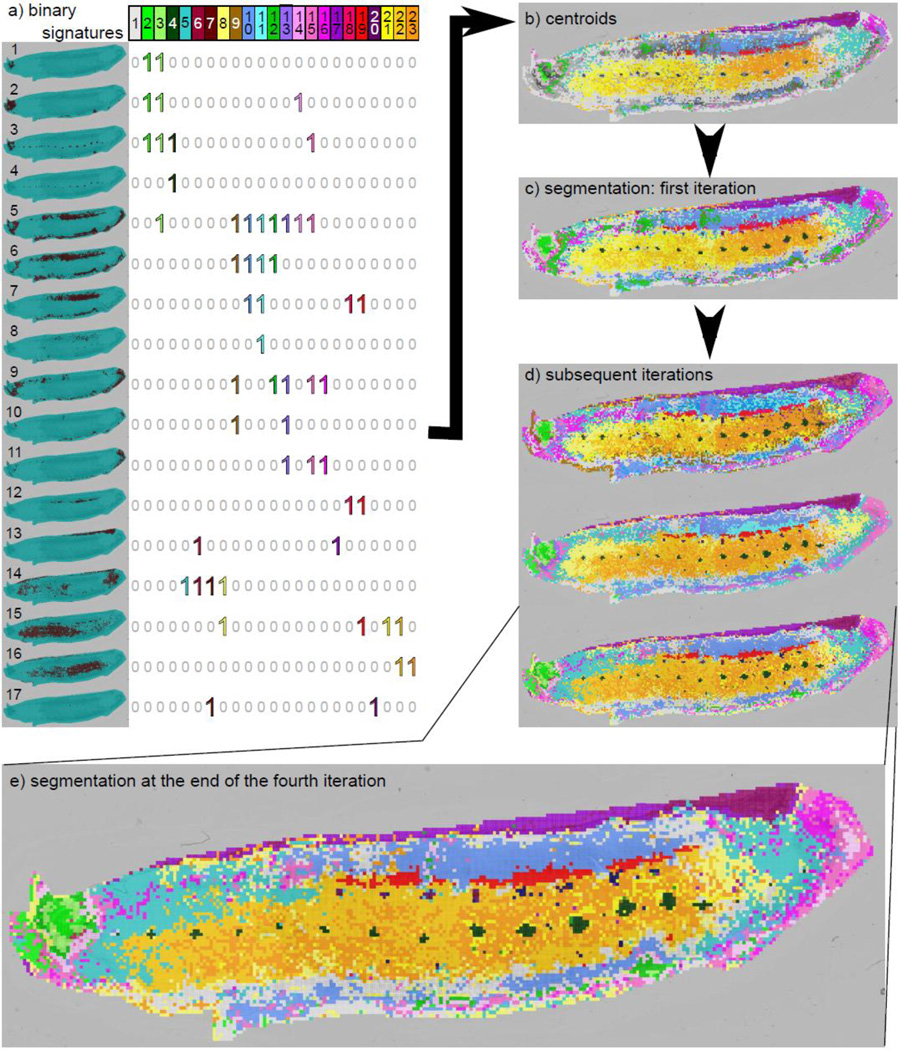
Binary spot signatures and leech segmentation maps. a) The dominating binary signatures. Each row represents a clustered query-result and each column represents a selected binary signature. Regions of interest may show some overlap. For example, the centroid for the heart (columns 18 and 19) also shows expression in the lateral region (row 7) thus resulting in binary signatures containing 1's in both rows 7 and 12. b) Spots corresponding to each of these binary signatures. These are used as centroid for clustering. These centers already reveal the major segments. c) New image-segmentation resulting from the reassignment of spots to the closest centroids. d) Refinement of the segmentation over subsequent iterations. e) The segmentation at the end of 4 iterations (run without any user intervention).

Figure 5.

Results for the rat brain slice dataset. Basic anatomy is provided for reference in Supplemental Figure 13b. The triplet of images associated with each query is composed of the corresponding original query, the weighted intensity image and the log-odds score image (outward towards the middle). The middle panels describe the result of hierarchical clustering after the first iteration. The two images in each cluster represent the resulting average log-odd scores and the binary image after votes. The bottom panels show the image-segmentation results after subsequent iterations. The results show clear demarcations of the morphology.

A key finding of our previous work⁹ was that, given a region of interest (ROI) defined by an image-segment (or collection of MSI spots) I, we usually obtain a strong molecular signature for I, a collection of mass values that are preferentially expressed in spots in I. Then, the spectrum of each spot s can be compared to the molecular signature associated with I. We use this idea to judge the quality of segmentation. Informally, a segmentation is consistent if each segment I has a unique molecular signature that is shared with all spots in I and not with other spots. This consistency measure is independent of morphology, and allows us to discover signatures that cross known morphological boundaries.

Using the molecular signature defined by I as a `query', we can recruit other spots to the segment, refining the segmentation. Our method is reminiscent of iterative unsupervised clustering methods, like a k-means clustering. It starts by choosing an initial segmentation, each with a molecular signature (or `center'). Subsequent iterations repeat two steps: (a) each spot is assigned to the nearest of the k signatures (based on a query) and, (b) k new signatures are described from the recruited spots. Earlier methods consider each MALDI spot as a vector of intensities over mass-bins, causing the clustering is dominated by high intensity peaks. This has been typically circumvented by using scaling techniques, such as autoscaling, which have their own problems. We propose a different representation of each spot. Starting with a current image-segmentation ℐ, each spot is represented as an |ℐ|-dimensional vector of query-scores to each of the segments in |ℐ|, where |ℐ| is the number of clusters in the segmentation. Thus two spots are similar if they have similar scores against all clusters. To start the algorithm we need an initial segmentation. In our case, the initial segments can be chosen at random, or by partial user-input (semi-supervised). The initial segments are chosen to be small groups (only a few) of contiguous spots, but otherwise no spatial correlation is assumed.

In summary, three ideas describe AMASS (Algorithm for MSI Analysis by Semi-supervised Segmentation). (a) Rank based statistics are a useful discriminator for any current cluster, and this allows us to query. (b) Query-result consistency is a valid score for the validity of a cluster. (c) The scores of a spot against existing clusters can be used to compare and re-partition spots. In addition, we make available a computational tool implementing the algorithm which allows many other controls for user intervention.

We applied AMASS on multiple data sets, including a leech embryo data set obtained from a 12-day (E12) specimen that was dissected and prepared flat before mounting on the MALDI target, and a data set of a rat brain coronal section of 4.16 mm from Bregma with known anatomical structures. We show in the detailed results below that, in each case, a completely automated run provided fine-grained, biologically meaningful segmentations and their molecular signatures. The leech dataset was segmented into regions corresponding to head, tail and segmental ganglia of the central nervous system, nephridia, heart, and lateral and ventral regions. The rat brain dataset was segmented into many domains corresponding to well-defined anatomical regions, with some signatures corresponding to co-expression of molecules in distinct morphological regions.

2 Results

2.1 AMASS: Algorithm for MSI Analysis by Semi-supervised Segmentation

The input to AMASS is a set of MSI spots S. Each spot in S is defined by a spectrum: a collection of m/z values and associated intensities. Define an image-segment I simply as a collection of spots. An image-segmentation ℐ (=⋃I) of an MSI data-set is an incomplete partitioning of the spots into image-segments. By incomplete, we mean that each spot is assigned to at most one image-segment, but could be assigned to none. The output of AMASS is a segmentation ℐ = ⋃I into consistent segments such that most spots are assigned. AMASS works with an iterative refinement of segments.

Procedure AMASS (S, spectra) → ℐ, A, molecular signatures

1. Select an initial image-segmentation ℐ, chosen either by the user, or via random spot selection.

2. Repeat until (|S| < ε)

   1. Calculate A = Query (ℐ).

      • (* A[I, s] denotes the score for spot s against each segment I ∈ ℐ*)

   2. For all consistent segments I ∈ ℐ

      • (* see Methods 4.4, equation 10 for definition of consistency *)

        • •Output I ; Set S = S\I

          • (* A consistent spot is fixed and output *)

   3. Set ℐ ← Spot-partition(ℐ, A).

      • (* Recompute non-consistent segments based on scores in A *)

In practice, we iterate for a small number of rounds before terminating. The three main steps are a choice of Initial segmentation, the Query procedure, and the Spot-partition, and these are described below, along with results.

2.2 Initial Segmentation

The initial segmentation can be done in either a guided mode or in a blind mode. In a guided mode, the user provides the initial clustering. Typically, it is a list of regions of interest (ROIs) for which he/she would like to get additional information with spots outside the ROIs unassigned. Examples of guided initial segments are shown in Figure 2. The semi-supervised component of the algorithm will then return additional information about the segments or ROIs, specifically which areas have similar molecular signatures as well as the actual molecular signatures. In a blind approach, the algorithm automatically generates a large set of small random seed clusters. Subsequently, it merge and expand the appropriate seeds. An example of such random segmentation is shown in Supplemental Figure 3a.

Figure 2.

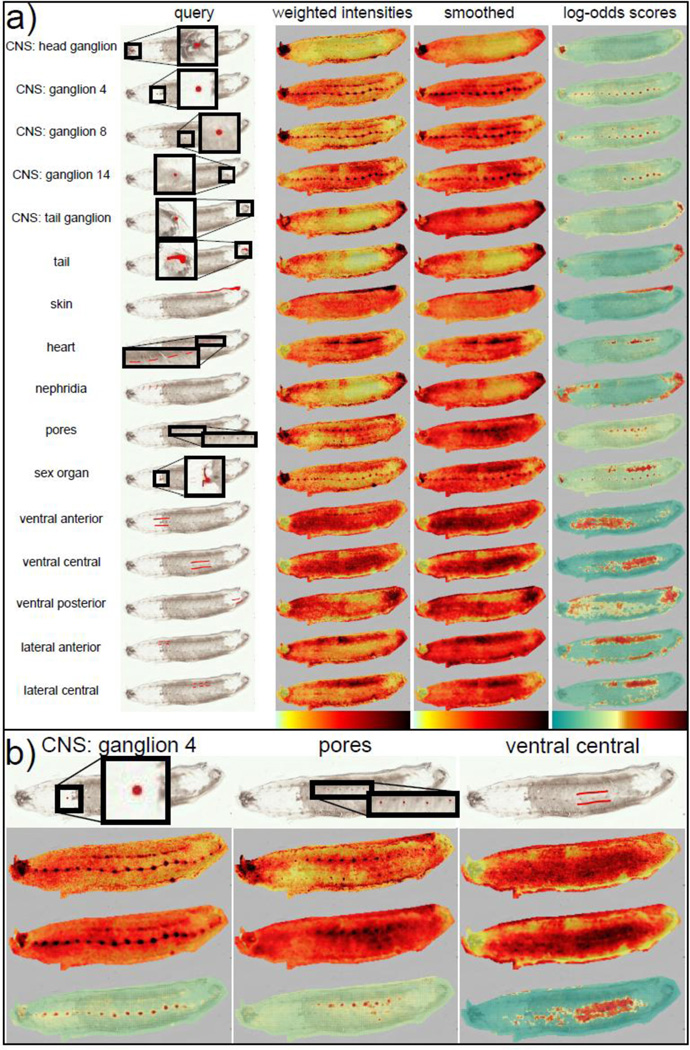
(a) List of queries and their associated results. Shown are on each row the original query, the corresponding weighted intensities image, the smoothed weighted intensities image and the log-odds scores image. Querying with specific image-segments results in the recruitment of other spots with similar molecular signatures. For example, querying with one ganglion or a few pores recruits the whole CNS or the rest of the pores respectively. (b) Detailed images for 3 different queries. We can see that while smoothing helps in cleaning noise on larger queries such as the ventral query, it can also cause the loss of some MALDI spots in the case of smaller regions, such as the pores.

2.3 Querying

The goal of querying is to compute A [I, s], a log-odds measure of similarity between the spectrum at a spot s and the molecular signature of spots in segment I. Denote the MALDI spectrum (m/z values and intensities) associated with spot s by a vector of intensities v_s; v_s[m] is the intensity at m/z value m (Methods 4.2). We use the following steps.

1. For each m/z value m and segment I, compute weight w_I, with w_I[m] describing the `importance' of m in discriminating I from S\I (Methods 4.2, equation 6).

2. Compute a weighted-intensity Z(I, s) = w_I·v_s.

3. Optionally, smooth the weighted intensities image.

4. Compute Pr (s ∈ I) and Pr(s ∉ I) using the distribution of Z (I, s) over spots in I and S\I, respectively (see Methods 4.2, equations 2 and 3)).

5. Set $\mathbf{A}[I,s]=\text{log}\left(\frac{\text{Pr}(s\in I)}{\text{Pr}(s\notin I)}\right)$

To showcase AMASS's ability to work with user defined queries (initial segments), we prepared queries informed by our knowledge of morphology. However, the queries were not precisely defined, as seen in Figure 2a. For example, ventral and lateral regions were defined by simple lines (for anterior, central and posterior) across the corresponding sections, while three of the ganglia were queried independently.

For each query I, we show three consecutive images in Figure 2a. The first two panels correspond to weighted-intensities Z (I, s) (before and after smoothing) and the third panel corresponding to the log-odds score A[I, s] computed as above. In every case, the scored images all highlight exactly the areas we would expect to see, illustrating the power of querying. Queries that are fairly complete, such as the skin, essentially recapture the region of the original query. Partial queries, such as the three single ganglia, each recover the entire central nervous system.

Figure 2b shows the advantages and costs of smoothing. The granularity inherent in MALDI imaging data is reduced by smoothing allowing for evenness in spot to spot weighted-intensities. Larger regions, such as the ventral central region, benefit by coalescing disjointed spots. This allows us to define unified regions in different section of the leech. However, very small and finely defined regions, such as the nephridiopores, lose in accuracy and localization. While we can see higher intensities in almost all the pores throughout the leech in the non-smoothed image, only the highest intensity pores are detectable in the smoothed image. We can also notice some diffusion of the signal in the CNS after smoothing. Spatial smoothing is an important part of some MALDI imaging analysis tools¹⁴. While AMASS provides smoothing as an option to reduce granularity, it is not used in our final segmentation results.

In the log-odds score images, we contrast the negative scores and the positive scores by showing them in green and red respectively (see scale in Figure 2). Thus, dark red spots in these images represents spots with molecular signatures very similar to that of the original query, and thus are recruited by the query, while dark green spots represent spots that are very unrelated. Partially related spots typically obtain scores closer to 0 (shown in pale yellow to light orange). For example, querying with the ventral posterior region (Figure 2b), expectedly results in partial recruitment across the entire ventral region including the ventral anterior region, with the highest scores in the ventral posterior regions. Thus, while the automated segmentation chooses a score threshold based on the distribution of the scores in the original query (see Methods 4.3), we make this an adjustable parameter.

Random Queries

While the algorithm is designed to let the user guide the study by choosing initial segments, choosing random spots as initial queries also results in a remarkably high quality segmentation. In Supplemental Figure 1, we show several examples of random seed-segments and the corresponding query-results, which are very similar to user-defined queries from the same morphological region (such as the CNS). In addition, query-results gain specificity in the next iteration as the new queries are based on molecular signatures found from each current iteration. Regions that are only defined by a few spots, such as the pores, are less likely to show on every random run; however, in general, several runs of the algorithm on a random seeding eventually find that region (data not shown).

Molecular signatures

In Figure 2a, one can observe that while a query consisting only of ganglion 4 recruits the entire CNS, more or less evenly, the query-results associated with ganglion 14 show stronger association in the more posterior ganglia. Thus, there are some differences in the molecular signatures associated with these queries in different regions from the same gross morphological feature (i.e. CNS). This specific case can be attributed to the rostrocaudal gradient in leech embryo development¹⁷. The head of the embryo is ~3 days older than the tail, and thus the ganglia may show different protein expression depending on their relative “age”. It is also possible that the differences reflect the innervation of different organs along the rostrocaudal axis.

As AMASS is a query/molecular-signature based segmentation, we can easily extract the molecular signatures associated with the query. As a test, we chose anterior ganglia 2–4, and posterior ganglia 13–15, and extracted differentiating score peaks from the querying module. In Supplemental Figure 2, we show the score peaks with weight greater than 0.7. Note that these are the weight associated to the m/z value, and not the rank statistics. While many of the m/z values show expression throughout the entire CNS, such as m/z ≈ 2524 and m/z ≈ 5418, some m/z values show a bias in intensities between the anterior and posterior regions. For example, at m/z ≈ 3299 and m/z ≈ 5273, high intensities values are present in ganglia 1–10 and 1–12 respectively but not in the rest of the CNS. On the other hand, at m/z ≈ 4377, high intensities are prevalent in posterior ganglia (8–14), but not anterior ganglia. These molecules will be prime candidates for targeted identification of peptides involved in specific stages of the leech neuronal development. In previous work⁹, we identified one of the molecule in the table (m/z ≈ 2474) which shows expression in both the anterior and posterior ganglia as a peptide from a novel gene, HmIF4, in the family of neurofilaments. Similar targeted identification can be done to target peptides for m/z values specific to anterior or posterior ganglia.

AMASS iteratively improves segmentation in a way that will create distinct molecular signatures for each segment. To test the signature strength of specific molecules, we observed the top 20 score peaks at least 10 Daltons apart for segments at successive iterations in leech and rat respectively (Supplemental Figures 4 and 5). In both cases, we can see that the peaks are overall conserved throughout the iterations. However, there are some changes from one iteration to the next. For peaks m/z ≈ 3508, 5417, 5570, we find that the weights increase with number of iterations while in peaks at m/z ≈ 3295 and 4007, the weight is high for the ganglia 5–6 initial segment, much lower in iterations 1 and 2, and not even in the top peaks for the ganglion 14 initial segment. These changes happens as the entire CNS is recruited to a segment starting with a single ganglion, and can be explained by observing the intensity images in Supplemental Figure 2. Peaks m/z ≈ 3508, 5417, 5570 show high intensity throughout the CNS; peaks at m/z ≈ 3653, 4377, 8564 show up in posterior ganglia, but not in the anterior ones. While m/z ≈ 8526 shows up as expressed in both, its intensities are high in ganglia 2–4 but lower in ganglia 5–6. Thus the contribution of individual peaks to the molecular signature, rises and falls with its expression in the segment, and allows for a fine grained exploration.

Molecular signatures for different regions of the rat brain also show interesting patterns (Supplemental Figures 6–11, as well as the corresponding m/z images in Supplemental Figures 7 and 8). We observe that several of the m/z values specifically expressed in the piriform cortex also show expression in the CA1-CA3 cell bodies, the CA3 cell bodies and the dentate gyrus (m/z ≈ 3454, 6223, 6272, 6646 in Supplemental Figure 7). Reciprocally, when querying the CA3 cell bodies, we find many of the same m/z values that also show expression in the piriform cortex (m/z ≈ 6626, 6275, 6648). However, the two queries do not share all peaks. There are many peaks from the piriform cortex query which do not show expression in the CA3 cell bodies, and there is peak which shows very strong signal in the CA cell bodies (m/z ≈ 8847) but no signal in the piriform cortex. The molecular relation between the two areas may be due to both containing apical dendrites of pyramidal neurons which are located in these regions. These shared peaks, illustrate the need for a tool that allows exploration of different segments, instead of a `black box' approach to segmentation.

2.4 Spot Partitioning

Hierarchical clustering of query-results

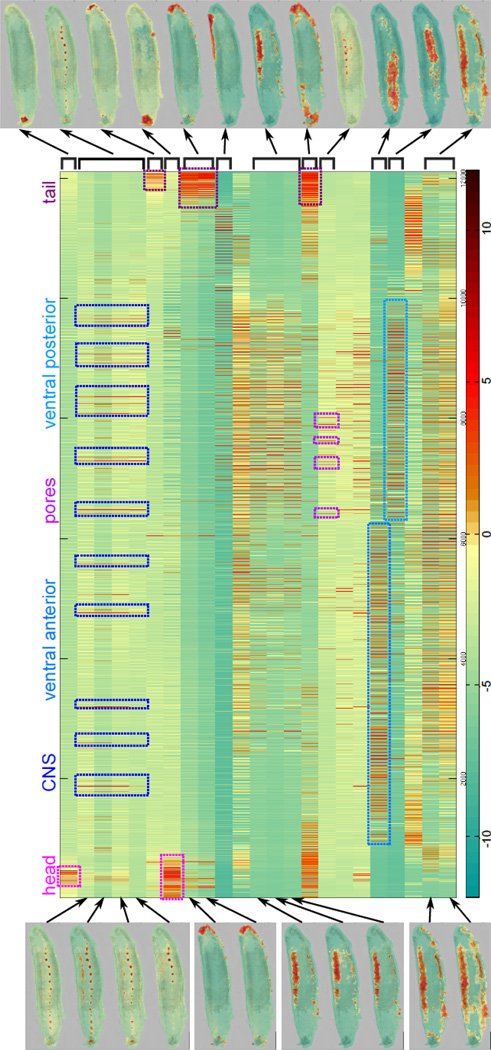
The result of the querying component is a matrix A [I, s] which contains the log-odds score of each spot s against each segment-query I. Each row of the matrix represents the result of querying a segment I, while each column is a vector of scores against each segment for a spot s. In Figure 3, we show the resulting matrix from querying the previous initial segments on the leech dataset, with scores encoded in a green-red color map. Spots are sorted by (x,y) coordinates; thus they are ordered from the top-left spot to the bottom-right spot, scanning vertically from left to right. When looking at the columns of the matrix, we can find columns with high scores throughout the same query-results, corresponding to certain morphological features. For example, the first four score images in the left column show higher log-odds scores in the CNS. The corresponding rows (2–5) show several bundles of vertical red lines (highlighted in the figure) which are consistent throughout the 4 rows and represent some of the ganglia. Some of the anterior ganglia do not show as strong scores in row 5, consistent with the image.

Figure 3.

Log-odds score matrix and hierarchical clustering. Each row of the matrix represents a query-result, with some of the corresponding log-odds images shown on the left-hand side. Spots are sorted by (x,y) coordinates; thus they are ordered from the top-left spot to the bottom-right spot, scanning vertically from left to right. When looking at the columns of the matrix, we can see high-scoring columns throughout several rows corresponding to specific morphological features, such as the ganglia in rows 2–5. Certain rows of the matrix also show very high similarity. These rows are clustered together and the result clustered query-result image is shown on the right-hand side. Rows (or query-results) that do not show high similarity to other rows end up in singleton clusters.

When looking at either the log-odds score images or the corresponding rows, we can see that the query-results from different segments are often very similar. This is expected as disjoint segments from the same morphological feature will have similar molecular signatures and thus MALDI spots will have similar scores against these segments. To merge these query-results, we perform hierarchical clustering on the matrix rows, or query-result vectors A [I, *] (Methods 4.3, equation 7), using the Tanimoto coefficient as a distance measure¹⁹. Here, we cluster to a Tanimoto coefficient of 0.65, but empirically AMASS is robust to a large range of thresholds. The left-side of Figure 3 shows images for query-results, while the right-hand side shows the clustered results (with mean scores). Regions that covered the same morphological features, such as CNS or lateral, ended up as one cluster, while regions that are only partially similar, such as full-lateral vs. posterior-lateral, remain separate. Some rows, such as the pores or the ventral regions, do not cluster with any other query-results and are shown as clusters of size 1 on the right-hand side.

Binary Signatures and Spot-partitioning

While the query-results clustering is robust, we expectedly find overlapping regions in the clustered query-results (Figure 3). For example, while some query-results cover the entire lateral region (last image on right-hand side), others cover only the posterior lateral region (7th image on right-hand side). This means that most spots in the posterior lateral region have high scores against two clustered query-results. Recomputing the segmentation involves clustering the spots that have similar pattern of scores across the current set of segments I. We do the following (also see Methods 4.3):

1. Set B = Binarize (A). Each distinct binary column b_s is a binary signature (see Methods 4.3, equation 8).

2. Choose a subset ℋ ⊆ 𝒢 of dominating signatures: signatures that are common to many spots.

3. For each dominating signature b ∈ ℋ, calculate the center c_b as the mean of spots that binarize to b (see Methods 4.3, equation 9).

4. Reassign each spot s to the center arg min _b‖a_s – c_b‖₂.

While the user has some ability to choose which binary signatures are to be maintained in the interactive mode, the algorithm can automatically determine which binary signatures are `dominating' (see Methods). Figure 4a describes the dominating binary signatures from the first iteration. For example, column 4 of the matrix (dark green) describes the binary signature for spots in the CNS ganglia (1 in rows 3, 4, and 0 elsewhere). Also, the last 3 columns (yellow, gold, orange) describe the ventral region (rows 15, 16). However, the figure reveals the complexity of segmentation. These 3 binary signatures specify molecules in the anterior ventral region only, in both the anterior and posterior ventral region, and the posterior ventral region only, respectively. The `correct' segmentation could be obtained by any combination of these 3 binary signatures. Moreover, if we look at the anterior ventral region (row 15), we see representation from multiple signatures, including those from the heart (column 19), and an undefined region (column 8), illustrating spatial distribution of molecules that would not be apparent in a final segmentation. It is worth noting that there are few spots in the heart only, thus resulting in binary signatures that cover both the heart and the lateral region (columns 18 and 19). Similarly, there are two query-results covering the head (row 1 and 2). Thus, in the resulting segmentation, the spots are divided between those in the "inner" part of the head, present in both query-results (columns 2 and 3) and those present in the "outer" part of the head, i.e. only in row 2 (column 14).

These dominating binary signatures are used to compute new centers. Figure 4b illustrates the spots that matched exactly to a center signature. We can see that these centers already reveal the major segments. The reassignment of spots to the center creates a new segmentation (Figure 4c). In the next iteration, we use each of the segments of this new segmentation as queries in the semi-supervised component, thus re-iterating through the process described above. Subsequent iterations result in a refinement of the segmentation (Figure 4d). The segmentation at the end of 4 iterations (run without any user intervention) is highlighted (Figure 4e), and reveals the power of AMASS. Unlike other clustering methods, the final segmentation clearly reveals small and large morphological regions including ganglia, pores, brain, lateral, and ventral regions along with their molecular signatures.

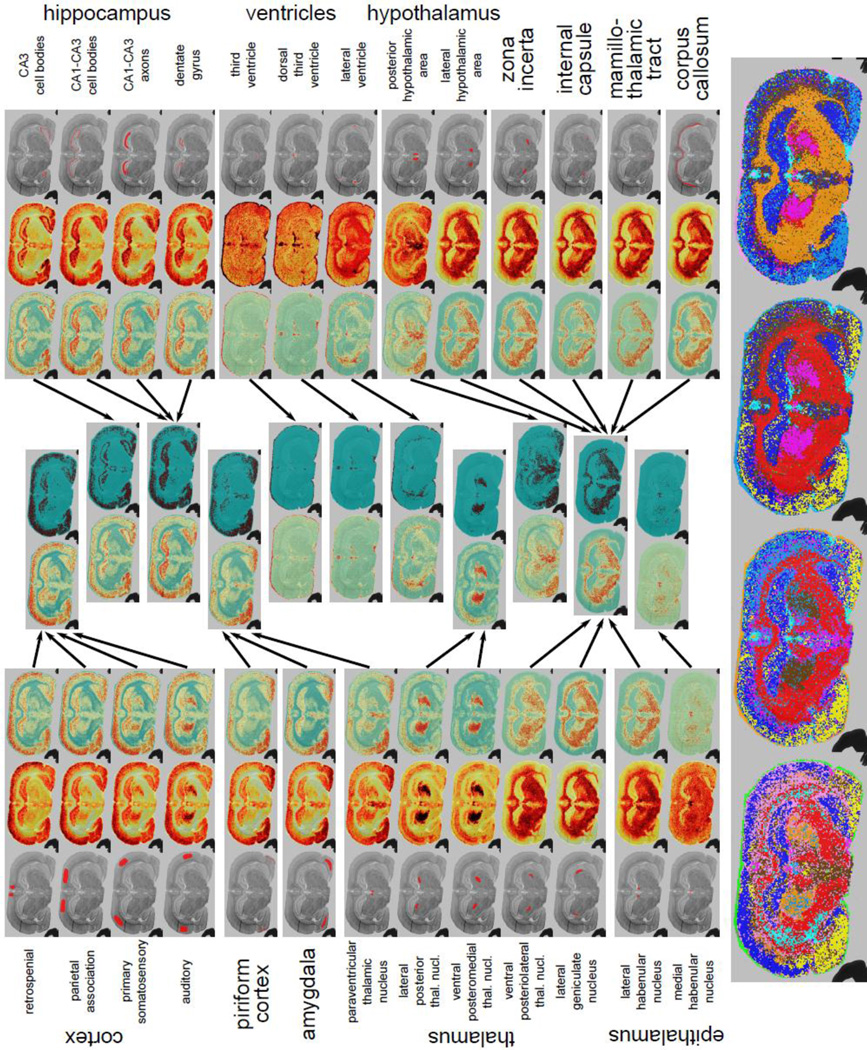
Similar results were obtained for the rat brain segmentation (Figure 5), with clear demarcations of the morphology. Basic anatomy is provided for reference in Supplemental Figure 13b. Specific initial queries behave as expected with a few surprises. In Figure 5, we have separated the queries based on the brain the substructure to which they belong (cortex, thalamus, hippocampus, etc). The triplet of images associated with each query is composed of the corresponding original query, the weighted intensity image and the log-odds score image (outward towards the middle). When looking at the cortex queries, we can see that the different upper cortex queries (retrospenial, parietal, primary somatosensory) all result in the larger upper cortex region. However, the region demarcated as the auditory cortex interestingly recruits a portion of the thalamus. The piriform cortex and amygdala, which are related to the neocortex, show some signal in the cortex with the majority of the signal in their respective regions. Interestingly, the paraventricular thalamic nucleus also shares a similar molecular signature to that of the amygdala and the piriform cortex. Other parts of the thalamus seem to split between two different regions; the lateral posterior thalamic nucleus and the ventral posteromedial thalamic nucleus recruit one shared reqion, while the ventral posteriolateral thalamic nucleus and the lateral geniculate nucleus recruit white matter. The internal capsule, mamillothalamic tract and corpus callosum, which are part of the white matter of brain which consists mostly of myelated axons, also recruit all white matter regions of the brain. This suggests that there is a distinct molecular signature for white matter, possibly due to myelin. As expected, all ventricles share the same molecular signature, which in this case should correspond to that of the matrix, explaning the signal at the edge of the sample. It is worth noting that some regions, such as the medial habenular nucleus and posterior hypothalamic area, have very particular molecular signatures, resulting in the recruitment of very specific regions. The middle panels describe the result of hierarchical clustering after the first iteration. The two images in each cluster represent the resulting average log-odd scores and the binary image after votes. The clustering step behaves as expected, with the different cortex query-results ending up in one cluster and all white matter query-results ending up in another. The bottom panels show the image-segmentation results after subsequent iterations. The rat brain is segmented in the different anatomical regions.

Finally, in Supplemental Figure 3, we show results for a completely random run on the leech embryo data set. The algorithm automatically generated an initial random segmentation (shown in panel a), composed of 100 seed-segments each consisting of a 1 to 3 adjacent MALDI spots. We ran 10 automatic iterations of the algorithm, once using 3x3 median smoothing, and once without any smoothing (panels b and c respectively). Segments resulting from the random segmentation also show the major morphological features of the leech and does not differ much from the guided approach. A few things to note are that the distinction between the anterior ventral and posterior ventral regions of the leech is not as well defined as in the guided approach, although it is still present. Also, in this specific run, a part of the top body margin clustered with the ventral region of the leech. Moreover, the nephridia, which have a weak signal, are not shown in this specific run, while the anterior ones are maintained in the guided analysis. This is due to the fact that small regions of interest do not show on every random run as there is a chance that no seed-segment is generated in the region. However, we do see the nephridiopores in the non-smoothed version of this specific run, signaling that a random segment must have been generated in one the nephridiopore. Finally, it is worth noting that the smooth segmentation provides much cleaner and more unified segments, but at the cost of some of the smaller segments, such as the pores or some of the anterior ganglia, which are completely lost by the final segmentation.

3 Discussion

MALDI imaging is rapidly becoming a technique of choice for surveying and discovering proteins and peptides that have spatially distinct signatures of expression. The large multi-dimensional nature of the data sets (expression of ~10³ molecular species in ~10⁴ spots) makes the mining for knowledge difficult. Unsupervised approaches seek to segment the tissue section into regions, each with a distinct molecular signature. However, classical segmentation techniques are often based on clustering molecules that have similar expression patterns. The quality of segmentation is often judged by its congruence with known morphology.

Here, we argue that these approaches do not work as well if there are small segments with low to medium abundance mass values. Instead, we propose a semi-supervised approach that ranks mass values by their spatial discrimination. Our results lead to consistent discovery of very fine segments (organs with 2–3 spots at 50µm resolution). Also, our query based techniques often reveal novel relationships, such as co-expression of molecules in the auditory cortex and portions of the thalamus in rat brain.

The next step in the process, is the actual identification of peptides corresponding to the molecular signatures. This remains a challenge even with progress in in situ trypsinization and other MS/MS fragmentation techniques. Further refinement of the discover of molecular signatures, and the identification of peptides will contribute to a novel tool for exploring the role of molecules in specific cellular phenotypes.

4 Methods

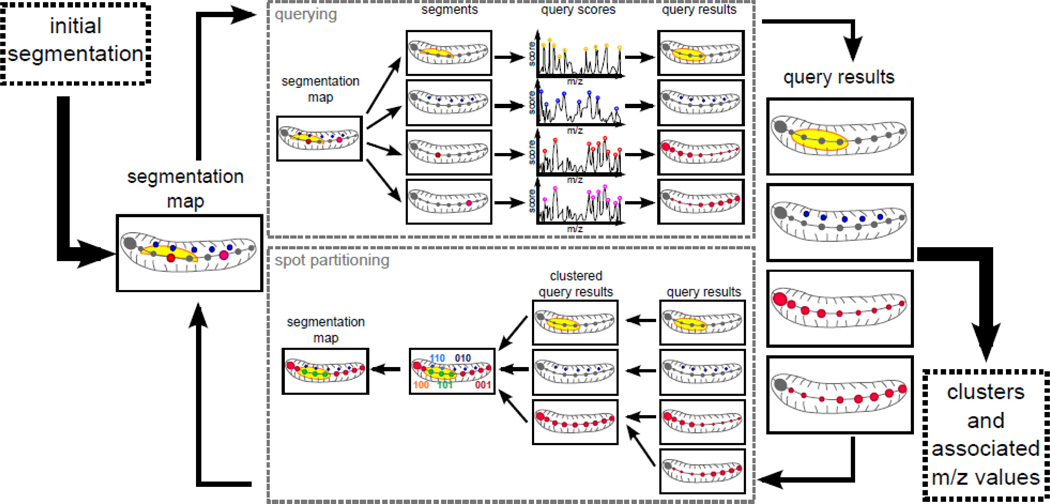
We first acquire MS Imaging data on the animal/section. We convert the data into our own lossless format and normalize it. As shown on Figure 1, the algorithm consists of two main components: a semi-supervised component and a partitioning component. The semi-supervised component performs a query for each of the original segments. It returns the molecular signature specific to the segment, as well as all areas sharing similar molecular signatures. The partitioning component assigns each spot to 0 or 1 cluster creating a (potentially partial) segmentation map. After selection of initial clusters, the algorithm iteratively runs these approaches fixing high-accuracy clusters along the way. While the algorithm can be run in a completely automatic mode, the main goal is to provide the user with easy control at each step of the way. Thus, it is possible for the user to choose which clusters to fix, keep or discard at each iterations. This allows the user to fine tune the results without “tweaking” parameters. The final output is a segmentation map with associated areas and molecular signatures for each cluster.

Figure 1.

Main workflow overview. First, we need an initial image- segmentation, which can either be defined randomly or by the user. In the querying component, each of the segment from the image-segmentation is used as a query and top-scoring m/z peaks are retained. A log-odds score is calculated for each spot and each query; this score represents the likelihood of a spot belonging to that query. The resulting set of scores per query forms a set of query-results. These are used as input to the spot partitioning component. In this component, the highly similar query-results are clustered together. We then obtain binary signatures for each of the spots and retain the dominating ones as cluster centroids. Clustering the all spots to the closest centroid results in a new image-segmentation. The whole process can be run iteratively until the quality of the segmentation is satisfactory.

4.1 Data Acquisition

Leech embryo

For the leech embryo analysis, we selected a specimen at stage E12 (12 days of development at room temperature), when the segmented nervous system and other organs like the nephridia, have clearly defined boundaries and are in a sufficiently advanced degree of molecular differentiation that specific signatures can be expected. The embryo was opened along the dorsal midline and the yolk removed, then pinned flat, exposed for 1–2 min to methanol to harden the tissues, finally placed on metal-coated (ITO) glass slides with the internal surface exposed and immediately dried. After recording transmitted light images to document the gross morphology of the specimen, it was coated with several layers of special solid ionic matrices (CHCA/Aniline), using a manual pneumatic TLC sprayer (VWR, Strasbourg, France). Such matrices have proven to be very efficient for peptide/protein analysis directly from tissue sections. MALDI direct analyses of tissues and MALDI Imaging were performed on a MALDI-TOF/TOF instrument (Ultraflex II, Bruker Daltonics, Germany) over 38837 m/z values from 12115 locations, generally sampling the embryo completely in a rectangular raster of points 60 µm apart. We refer to previous work⁹ for a more detailed description of the sample preparation. The complete data-set is a collection of spectra, each associated with a `spot' on the leech surface. Conceptually, the data can be represented as a collection of triples 〈m,s,I,_m,s〉 describing the spectral intensity I_m,s at each spot s, and m/z value m. The spectral intensity depends upon the abundance of the molecular species among other factors. While the intensities of different molecules cannot be compared directly, the relative intensity of the same molecule (mass value m) at different spots is a measure of the relative abundance of the molecule.

Rat brain slice

Cryosections of 10µm thickness were cut on a cryostat (CM 1900 UV, Leica Microsystems GmbH, Weltzar, Germany) and transferred to a precooled, conductive indium-tin-oxide (ITO) coated glass slide (Bruker Daltonik GmbH, Bremen, Germany). The sections were washed twice for 1 min in 70% ethanol, and once for 1 min in 96% ethanol and then dried in a vacuum desiccator. The matrix (Sinapinic acid at 10 mg/mL in 60% acetonitrile and 40% water with 0.2% trifluoroacetic acid) was applied using the ImagePrep device (Bruker Daltonik GmbH) following a standard protocol. Mass spectra were acquired on a MALDI-TOF instrument (Autoflex III; Bruker Daltonik GmbH) equipped with a 200 Hz smartbeam II laser. MALDI measurements were performed in linear positive mode at a mass range of 2.5 kDa to 25 kDa. The lateral resolution for the MALDI image was set to 80µm. A total of 200 laser shots were summed up per position.

4.2 Query

We compute A:S × 2^S → ℜ, where

$$\mathbf{A}[I,s]=\text{log}\frac{\text{Pr}(s\in I)}{\text{Pr}(s\notin I)}$$ (1)

The probability estimates are computed empirically. Consider a score function Z: S × 2^S → ℜ where Z(I, s) denotes the `score' of spot s against the segment I. The only requirement on Z (see next subsection) is that the scores in I are higher than S\I, and well separated. We estimate Pr(s ∈ I) by empirically computing the probability that a randomly chosen spot in I would score lower than Z(I, s)

$$\text{Pr}(s\in I)\approx \text{Pr}(\mathit{Z}(I,t)\le \mathit{Z}(I,s)|t\in I)$$ (2)

Likewise,

$$\text{Pr}(s\notin I)\approx \text{Pr}(\mathit{Z}(I,t)\ge \mathit{Z}(I,s)|t\notin S\backslash I)$$ (3)

Weighted intensity scores

The spectrum acquired on spot s is a collection of m/z values and intensities. We do a simplified peak selection, choosing the top 5 scoring m/z values (averaged over a 1 Da window) in a scrolling window of 50 Daltons. The selected peaks are represented by a vector v_s, where v_s[m] is the intensity at m/z value m. Second, we compute a vector of weights w_I, where w_I[m] describes the `importance' of a peak at m in separating spots in I from S\I. Intuitively a spot s belongs to I if w_I and v_s are correlated. Therefore, we choose the weighted-intensity score function

$$\mathit{Z}(I,s)={\mathbf{w}}_I·{\mathbf{v}}_s$$ (4)

In earlier work⁹, we computed the Wilcoxon-Mann-Whitney ρ-statistic. ρ_I[m] is a measure of how well the peak at m separates spots in I from those in S\I. Formally, for randomly chosen spots s ∈ I,t ∈ S\I

$${\rho }_I(m)=\text{Pr}(s[m]\ge t[m])$$ (5)

While we could use ρ_I[m] directly as the weighting function, we choose

$${\mathbf{w}}_I[m]=\{\begin{array}{cc}2\Vert {\mathbf{w}}_I{\Vert }^{-1}{({\rho }_I[m]-0.5))}^P\hfill & \text{for}{\rho }_I[m]\ge 0.5\hfill \\ 0\hfill & \text{for}{\rho }_I[m]<0.5\end{array}$$ (6)

Here, ‖w_I‖⁻¹ is a normalizing constant. For ρ > 1, w_I[m] increases sub-linearly, staying close to 0 for intermediate values of ρ_I[m], and then increasing sharply to 1, thus allowing the strongly discriminative m/z values to be sharply upweighted versus multiple low-discriminating mass-values. As ρ increases, so does the weight of the top m/z discriminative values, causing the query-result to be more specific to the original query.

Smoothing

Optionally, image smoothing may be applied on the weighted intensity images in order to suppress the pixel-to-pixel variability. As shown in Alexandrov et al.¹⁴, the advanced image smoothing methods applied to mass intensity images significantly improve the segmentation results. In contrast to Alexandrov et al.¹⁴, we use simple median smoothing (3x3 window).

4.3 Spot Partitioning

Hierarchical clustering

Since highly related queries return very similar results, we cluster the rows of matrix A. We use hierarchical clustering with the Tanimoto coefficient as a distance function between segments I₁, I₂, computing distance to the average log-odds image in the case of clustered-segment.

We denote the clustered-segments as I′, and let I → I′ if and only segment I is clustered into I′. We compute cluster-scores for spots as

$$\mathbf{A}\prime [I\prime ,s]={\text{mean}}_{\{I\to I\prime \}}(\mathbf{A}[I,s])$$ (7)

Spot-vector binarization

We select a threshold score t_I for each I based on the distribution of scores in I and S\I. Intuitively spot s belongs to I if A[I, s]≥t_I. Next we merge the segments in C by taking a majority vote. Denote matrix B as a binary matrix with rows corresponding to segment-clusters.

$$\mathbf{B}[I\prime ,s]=\{\begin{array}{cc}1\hfill & \text{if}\#\{I\to I\prime :\mathbf{A}[I,s]\ge t_I\}/\#\{I\to I\prime \}\ge \frac{1}{2}\\ 0& \text{otherwise}\hfill \end{array}$$ (8)

Dominating signatures as centers

The columns of B corresponding to spot s describe a `binary-signature' for spot s. In the ideal case, strong segment-clusters should have a unique signature and all spots contained in the cluster have the corresponding signature. For each cluster, denote the most frequent signatures as dominating, if it has sufficient frequency.

Spot partitioning

In the final step of the iteration, we use the dominating signatures to determine cluster centroids and partition spots by assigning the remaining spots to these clusters. Let a'_s denote the cluster-scores (A'[*,s]) for spot s. For each dominating signature b, we define the associated set of spots S_b = {s: b_s = b}. We then define a centroid c_b for each dominating signatures as the mean of the cluster-scores of spots

$${\mathbf{c}}_{\mathbf{b}}={\text{mean}}_{\{s\in S_{\mathbf{b}}\}}(\mathbf{a}{\prime }_s)$$ (9)

We also add a zero centroid to the set, which is either the centroid of all spots not belonging to any query-result if such spots exists, or a zero vector if there are no such spots. Each spot s is reassigned to the closest centroid arg min _b‖a′_s–c_b‖₂. Overall, spot partitioning corresponds to a single pass of k-means clustering, and provides the segmentation for the next iteration.

4.4 Query consistency

We measure segmentation based on consistency of query (see Supplemental Figure 10). For segment I, denote S_I as the set of all spots such that A[I, s]≥t_I. In the ideal scenario, querying a segment will return all the spots in that cluster and only those spots (I = S_I). We use the Jaccard similarity coefficient to measure consistency of I as

$$\text{consistency}(I)=J(I,S_I)=\frac{|I\cap S_I|}{|I\cup S_I|}.$$ (10)