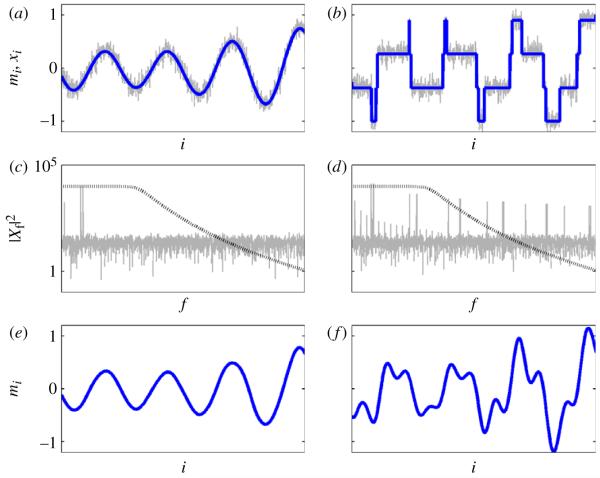
Figure 2.

Noise removal from PWC signals is a task for which no linear filter is efficient, because, for independent noise, the noise and the PWC signal both have infinite bandwidth, e.g. there is no maximum frequency above which the Fourier components of either have zero magnitude. (a) A smooth signal (blue) with added noise (grey), constructed from a few sinusoidal components of random frequency and amplitude; (b) a PWC signal (blue) with added noise (grey), constructed from ‘square-wave’ components of the same frequency and amplitude as the smooth signal. (c) (Discrete) Fourier analysis of the noisy smooth signal shows a few large magnitude, low-frequency components and the background noise level that occupies the whole frequency range. (d) Fourier analysis of the noisy PWC signal in (b), showing the same low-frequency, large magnitude components, but also many other large magnitude components across the entire frequency range (which are harmonics of the square-wave components). The black, dotted line in (c) and (d) shows the frequency response (magnitude not to scale) of a low-pass filter used to perform noise removal; this is applied to the noisy, smooth signal in (e) and the noisy PWC signal in (f). It can be seen that while the smooth signal is recovered effectively and there is little noticeable distortion, although noise is removed from the PWC signal, the jumps are also smoothed away or cause spurious oscillations (Gibb’s phenomena). (Online version in colour.)