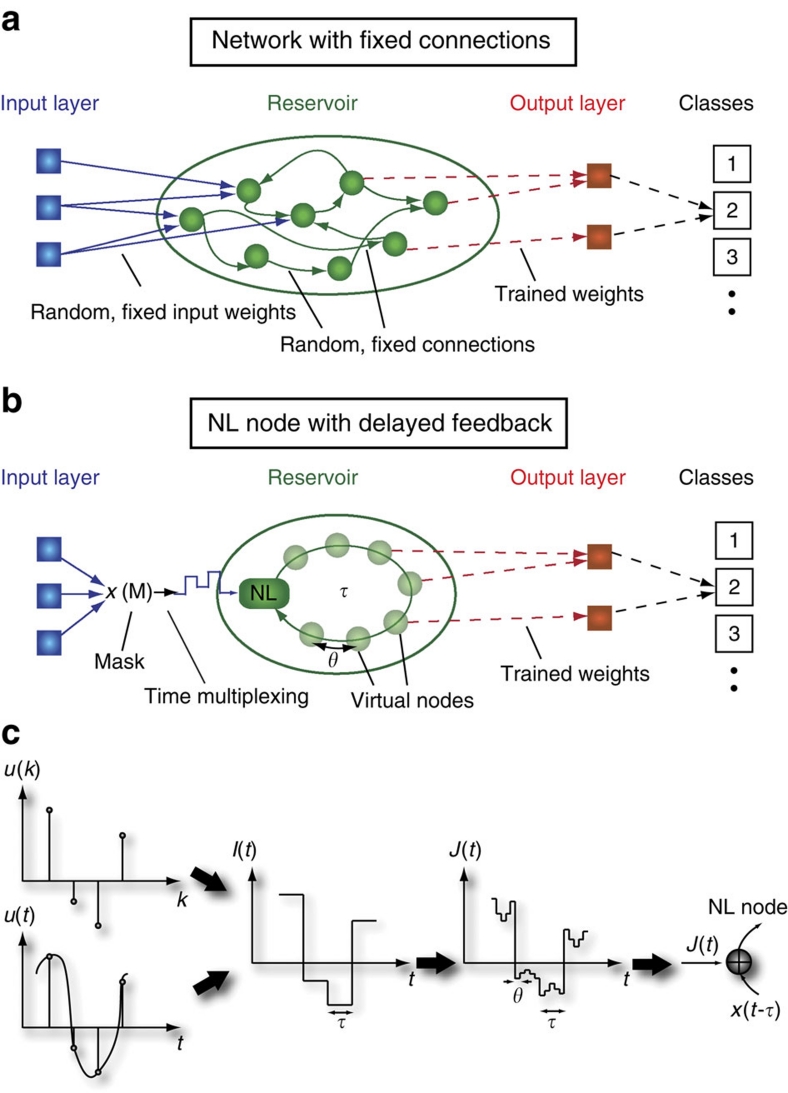
Figure 1. Sketch of RC schemes.

(a) Classical RC scheme. The input is coupled into the reservoir via a randomly connected input layer to the N nodes in the reservoir. The connections between reservoir nodes are randomly chosen and kept fixed, that is, the reservoir is left untrained. The reservoir's transient dynamical response is read out by an output layer, which are linear weighted sums of the reservoir node states x_i(t). The output 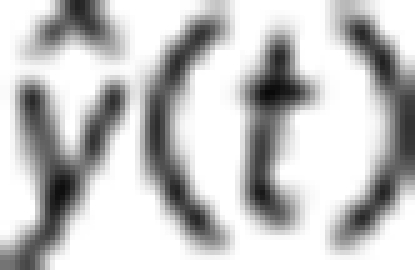thus has the form 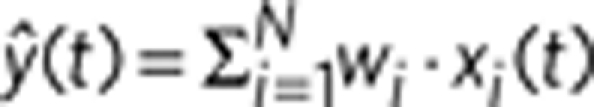. The coefficients w_i of the sum are optimized in the training procedure to best project onto the target classes. (b) Scheme of RC utilizing a nonlinear node with delayed feedback. A reservoir is obtained by dividing the delay loop into N intervals and using time multiplexing. The input states are sampled and held for a duration τ, where τ is the delay in the feedback loop. For any time t₀, the input state is multiplied with a mask, resulting in a temporal input stream J(t) that is added to the delayed state of the reservoir x(t−τ) and then fed into the nonlinear node. The output nodes are linear weighted sums of the tapped states in the delay line given by 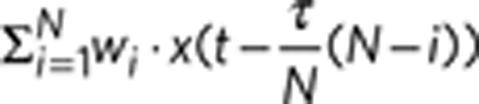. (c) Scheme of the input data preparation and masking procedure. A time-continuous input stream u(t) or time-discrete input u(k) undergoes a sample and hold operation, resulting in a stream I(t) that is constant during one delay interval τ before it is updated. The random matrix M defines the coupling weights from the input layer to the virtual nodes. The temporal input sequence, feeding the input stream to the virtual nodes, is then given by J(t)=M×I(t).