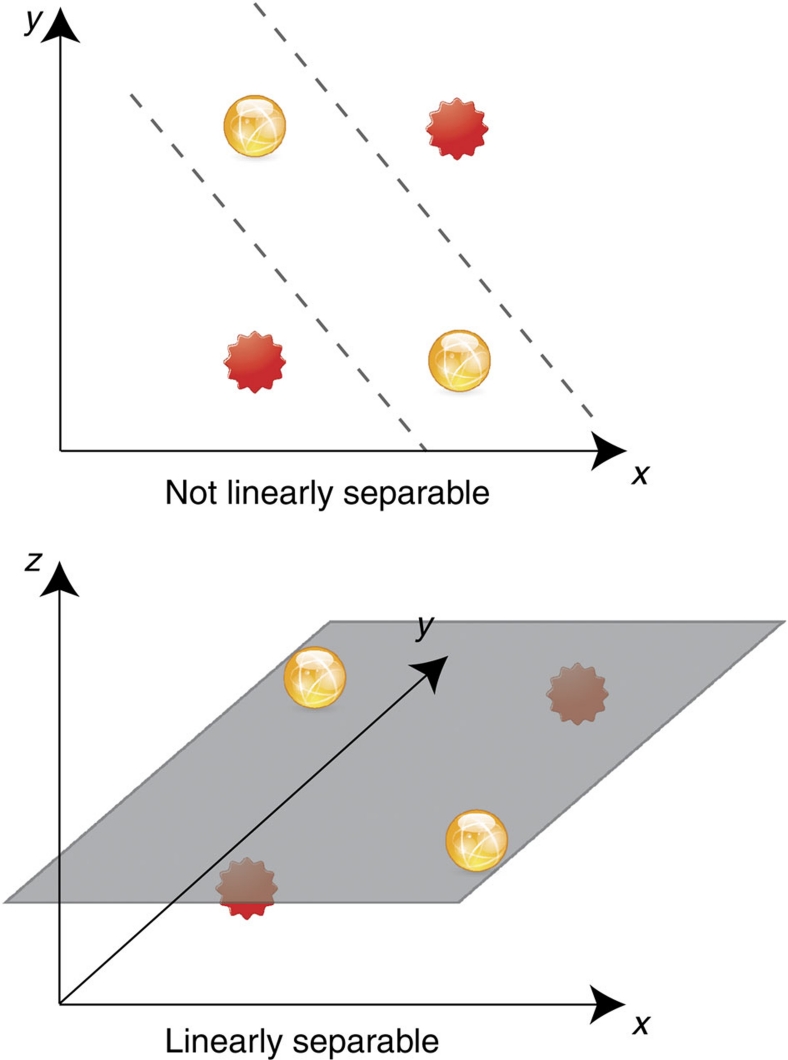
Figure 2. Illustration of linear separability.

It is well known that a non linear mapping from a small dimensional space into a high-dimensional space facilitates classification. This is illustrated in a simple example: In (a) a two-dimensional input space is depicted, in which the yellow spheres and the red stars cannot be separated with a single straight line. With a nonlinear mapping into a three-dimensional space, as depicted in (b), the spheres and stars can be separated by a single linear hyperplane. It can be shown that the higher dimensional the space is, the more likely it is that the data become linearly separable, see for example, ref. 14. RC implements this idea: the input signal is nonlinearly mapped into the high-dimensional reservoir state through the transient response of the reservoir. Furthermore, in RC the output layer is a linear combination with adjustable weights of the internal node states. The readout and classification is thus realized with linear hyperplanes, as in the figure.