Figure 2. A mathematical model characterizing the effects of lactate production on changes in glucose uptake and NAD+ regeneration rates.
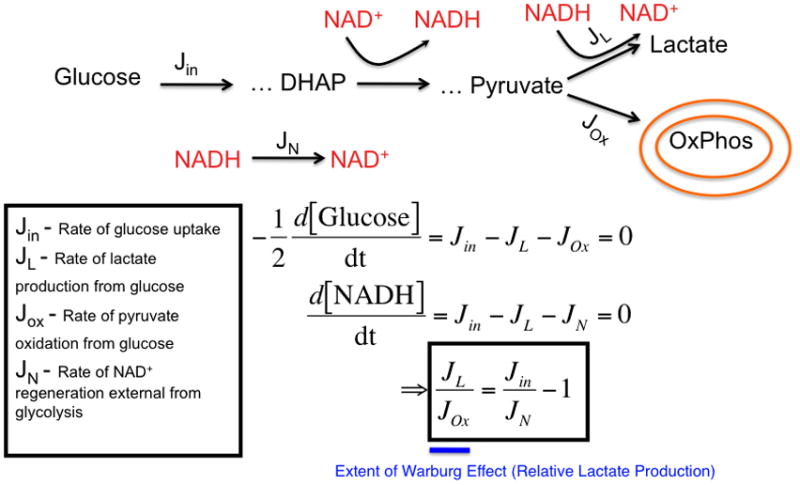
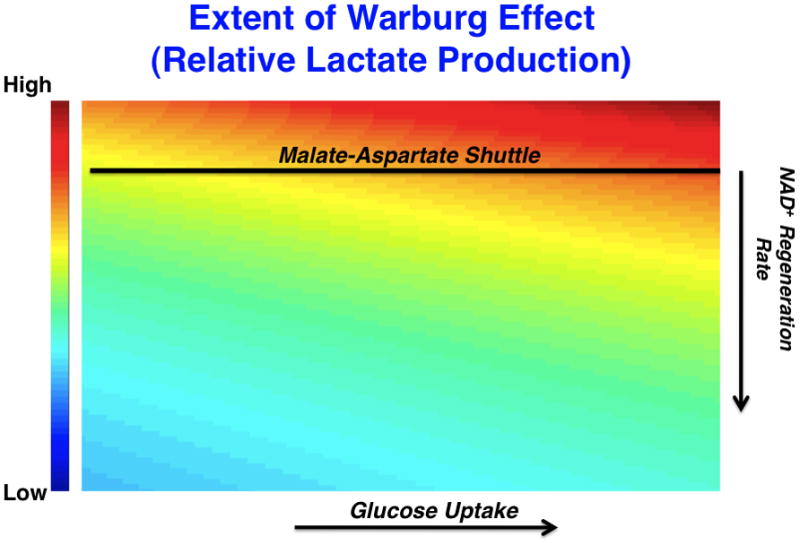
(left) A model that considers the stoichiometric balance of carbon and NAD+/NADH-generating fluxes in glycolysis and peripheral metabolism. In the model, glucose uptake and capture resulting in the generation of 2 glycolytic carbon units occurs at a rate, Jin. Glucose is metabolized through a series of steps eventually reaching an intermediate dihydroxyacetone phosphate (DHAP) at which point it is oxidized to produce NADH from NAD+. Eventually a glycolytic carbon unit reaches pyruvate where it can be reduced to produce lactate and generate NAD+ from NADH at a rate, JL. Alternatively, pyruvate can enter the mitochondria at a rate JOx. External to glycolysis, NAD+ is regenerated NADH by redox shuttles and other mechanisms. As a result, two differential equations can be written describing mass conservation of carbon and redox status and, at steady-state, can be solved for the relative rate of JL over JOx which is a measure of the extent of the Warburg effect or relative glucose-derived lactate production (in blue). (right) A representative plot of the ratio of the rate of lactate production to the rate of pyruvate entry into the mitochondria as a function of glucose uptake and NAD+ regeneration rate is shown. The extent of the Warburg effect is thus proportional to the rate of glucose uptake and inversely proportional to the rate at which NAD+ is regenerated by sources outside of Lactate dehydrogenase. The straight line represents an estimated rate of NAD+ from shuttles such as the malate-aspartate shuttle that is limited by mitochondrial transport rates. As glucose uptake increases (in the direction of the arrow on x-axis), the relative amount of glycolytic flux diverted to lactate production increases. As the rate at which NAD+ is regenerated increases (in the direction of the arrow on the y-axis), the relative amount of glycolytic flux diverted to lactate production decreases. These equations are obtained strictly from mass conservation of a model involving glucose entering glycolysis and leaving as either pyruvate or lactate. If the model allows for carbon units to exit glycolysis, then this would result in lowering the effective Jin in the equation.
