Skip to main content
PMC home page
Annals of Botany logoLink to Annals of Botany
. 2011 Sep 21;108(7):1337–1345. doi: 10.1093/aob/mcr225

Is leaf dry matter content a better predictor of soil fertility than specific leaf area?

J G Hodgson 1,*, G Montserrat-Martí 2, M Charles 3, G Jones 3, P Wilson 4, B Shipley 5, M Sharafi 6, B E L Cerabolini 7, J H C Cornelissen 8, S R Band 4, A Bogard 3, P Castro-Díez 2, J Guerrero-Campo 2, C Palmer 3, M C Pérez-Rontomé 2, G Carter 3, A Hynd 3, A Romo-Díez 9, L de Torres Espuny 10, F Royo Pla 10
PMCID: PMC3197453  PMID: 21948627

Abstract

Background and Aims

Specific leaf area (SLA), a key element of the ‘worldwide leaf economics spectrum’, is the preferred ‘soft’ plant trait for assessing soil fertility. SLA is a function of leaf dry matter content (LDMC) and leaf thickness (LT). The first, LDMC, defines leaf construction costs and can be used instead of SLA. However, LT identifies shade at its lowest extreme and succulence at its highest, and is not related to soil fertility. Why then is SLA more frequently used as a predictor of soil fertility than LDMC?

Methods

SLA, LDMC and LT were measured and leaf density (LD) estimated for almost 2000 species, and the capacity of LD to predict LDMC was examined, as was the relative contribution of LDMC and LT to the expression of SLA. Subsequently, the relationships between SLA, LDMC and LT with respect to soil fertility and shade were described.

Key Results

Although LD is strongly related to LDMC, and LDMC and LT each contribute equally to the expression of SLA, the exact relationships differ between ecological groupings. LDMC predicts leaf nitrogen content and soil fertility but, because LT primarily varies with light intensity, SLA increases in response to both increased shade and increased fertility.

Conclusions

Gradients of soil fertility are frequently also gradients of biomass accumulation with reduced irradiance lower in the canopy. Therefore, SLA, which includes both fertility and shade components, may often discriminate better between communities or treatments than LDMC. However, LDMC should always be the preferred trait for assessing gradients of soil fertility uncoupled from shade. Nevertheless, because leaves multitask, individual leaf traits do not necessarily exhibit exact functional equivalence between species. In consequence, rather than using a single stand-alone predictor, multivariate analyses using several leaf traits is recommended.

Keywords: Ellenberg numbers, functional traits, leaf density, leaf nitrogen, leaf size, leaf thickness, relative growth rate (RGR), shade tolerance, variation in trait expression

INTRODUCTION

A key element controlling function in terrestrial ecosystems is soil fertility, and this factor is an important environmental driver of the fundamental trade-off in leaves involving the rapid acquisition of nutrients and conservation of resources within well-protected tissues (see Lambers and Poorter, 1992; Reich et al., 1992; Garnier and Laurent, 1994; Grime et al., 1997; Wright et al., 2004; Shipley et al., 2006). The ensuing ‘worldwide leaf economics spectrum’ (Wright et al., 2004) is accepted as a key axis of specialization between soft, mesomorphic leaves in productive habitats and tough, fibrous ones in unproductive habitats. Plant growth rate, palatability to unspecialized herbivores, nutrient recycling and agricultural yield all scale along this ‘worldwide leaf economics spectrum’ (Grime et al., 1997; Díaz et al., 2004; Wright et al., 2004; Hodgson et al., 2005b).

Two easily measured predictors of this important ecological axis have emerged, leaf dry matter content (LDMC; dry leaf mass/water-saturated fresh leaf mass) and specific leaf area (SLA; leaf area/leaf dry mass) or its reciprocal, leaf dry mass per unit area (LMA) (see Cornelissen et al., 2003; Poorter et al., 2009). The soil fertility indicator of choice is SLA and, for example, Westoby's (1998) leaf–height–seed (LHS) plant ecology strategy scheme in which SLA alone defines the fertility axis is still widely accepted (e.g. Laughlin et al., 2010; De Frenne et al., 2011). The use of SLA is, however, problematic. As Witkowski and Lamont (1991) emphasize and Wilson et al. (1999), Craine and Towne (2010) and Kitajima and Poorter (2010) subsequently remind us, SLA is the product of two variables, leaf tissue density (LD) and leaf thickness (LT): leaf tissue density is closely related to leaf dry matter content (LDMC) (Shipley and Vu 2002), leading to eqn (1).

graphic file with name mcr225eqn1.jpg (1)

The inclusion of LT as a component of SLA in eqn (1) presents both a practical and a theoretical dilemma. Although LT has been investigated in detail by Vile et al. (2005), it is not frequently measured. It is not included in the handbook of methods for measuring functional traits for the global flora (Cornelissen et al., 2003) or in many international databases (e.g. Kleyer et al., 2008). Moreover, its ecological relevance is suspect. To the best of our knowledge, LT has never been recommended as an independent predictor of soil fertility and growth rate. Rather, its lower and upper extremes appear to identify habitat shade and leaf succulence, respectively (Vendramini et al., 2002; Lusk et al., 2008), and particularly with respect to growth responses at different light intensities there are important issues of plasticity. Sun leaves have a thicker lamina and lower SLA: the SLA of shade leaves can be twice that of sun leaves on the same plant (see Popma and Bongers, 1988; Cornelissen, 1992; Dong, 1993). Moreover, sun leaves exhibit higher net rates of photosynthesis, contain a greater quantity of photosynthetic apparatus (with attendant physiological adaptations) and increased gaseous exchange is facilitated by a higher density of stomata (Bolhàr-Nordenkampf and Draxler, 1993; Terashima et al., 2001).

Because LT impacts in this way on the expression of SLA, Witkowski and Lamont (1991), Wilson et al. (1999) and Craine and Towne (2010) prefer the use of LDMC. It is even easier to measure than SLA and is also routinely measured as an important general predictor of the ‘the worldwide leaf economics spectrum’ (e.g. by Kleyer et al., 2008). In addition, while SLA loses most of its biological interpretation in species whose photosynthetic organs do not have the typical planar form, LDMC remains well defined.

While we find the arguments pioneered by Witkowski and Lamont (1991) compelling, they have not been generally followed. The common interpretation of SLA as an indicator of soil fertility amongst ecologists represents a paradox. If LT is not strongly associated with soil fertility, shouldn't LDMC be the preferred functional trait in field studies as an indicator of adaptation to fertility? Moreover, if LT reflects important environmental (light or water) gradients, shouldn't SLA be deconstructed into its component parts and both LDMC and LT be included as independent functional traits?

This paper attempts to answer the above questions by assessing the relative merits of SLA and LDMC as predictors of rapid growth and soil fertility. First, using a data set of >2000 species, we confirm some generally accepted relationships [i.e. the approximate correspondence between LD and LDMC and that SLA is an inverse function of LDMC and LT; see eqn (1)] and assess whether these relationships are numerically identical in disparate ecological and taxonomic sub-sets of the data. We additionally examine the range of values and consider the importance of a fourth variable, leaf size (LA). Like the three leaf variables above, LA also affects construction costs (Givnish, 1976; Niinemets et al., 2007). Secondly, we attempt to validate each leaf attribute as a predictor of soil fertility. Using correlations, we identify the extent to which leaf attributes predict relative growth rate (RGR), leaf nitrogen content and Ellenberg ‘Nitrogen Figures’ (Ellenberg et al., 1992). These three characteristics are widely used in studies of soil fertility and related processes. Thirdly, we consider the ecological implications of SLA being a function of both LDMC and LT [eqn (1)]. In particular, since LT and SLA both vary between sun leaves and shade leaves, we assess variation in SLA, LDMC and LT in relation to different combinations of soil fertility and shade. Finally, on the basis of these analyses, we discuss the relative merits of SLA and LDMC as predictors of soil fertility.

MATERIALS AND METHODS

Data sources and measurements

SLA [leaf area (mm2)/leaf mass (mg)], LDMC (100 × dry mass of leaf/saturated mass of leaf), LT (mm, thickness measured between main veins) and maximum leaf size, LA (mm2) were abstracted from a large functional data set currently being prepared for publication. The measurement procedures are described in detail in Charles et al. (1997) and Wilson et al. (1999). They conform to the general recommendations of Garnier et al. (2001) and Cornelissen et al. (2003). In addition, because leaf volume was not measured, LD (mg mm−3) was estimated indirectly from eqn (1) as 1/(SLA × LT). To achieve numerical parity with LDMC, values of LD were multiplied by 100 prior to analysis. LT for leaves with prominent veins underestimates average leaf thickness and, had more time and resources been available, LD would have been determined more directly by measuring leaf volume as, for example, in Shipley and Vu (2002).

Data for SLA, LDMC and LT were obtained from the Unit of Comparative Plant Ecology, Department of Archaeology (Sheffield University), Instituto Pirenaico de Ecología (Zaragoza) and the senior author, and relate to plant material collected from unshaded habitats in Northern and Southern Europe and to a lesser extent the Near East and the Canary Islands. Values for leaf nitrogen concentration (leaf N) also originate from the database (see Hodgson et al., 2005a, 2010 for details). Maximum RGR values (RGRmax, g g−1 d−1) were abstracted from Grime and Hunt (1975) and Vile et al. (2006), and mean RGR values (RGRmean) from Cornelissen et al. (1996).

In most analyses, species were classified into ecological groupings on the basis of Grime et al. (2007), unpublished vegetation surveys and observed field distribution in Central England. Many Mediterranean species were similarly grouped according to Royo Pla (2006). For broad European analyses, phytosociologically related Ellenberg ‘Nitrogen Figures’, or soil fertility preference classes on a 1–9 scale, were abstracted from Ellenberg et al. (1992). ‘Nitrogen Figures’ are associated in the theoretically expected manner with growth and resource allocation studies (Thompson et al., 1993) and are strongly correlated with both field measures of soil productivity (Schaffers and Sykora, 2000) and foliar concentrations of nitrogen and phosphorus in the field (leaf N, r = 0·73, n = 91, P < 0·001; leaf P, r = 0·74, P < 0·001; leaf nutrient data from Thompson et al., 1997). Ellenberg ‘Light Figures’ have also been used. Nomenclature follows, preferentially, Stace (1997), but, where necessary, Tutin et al. (1964–80).

Analyses

After checking frequency distributions for normality and variance heterogeneity, it was necessary to present LDMC and LD as their square root, and to log10-transform the remaining variables prior to statistical analysis. Regressions all relate to the Type II of Warton et al. (2006). Except where otherwise stated, the remaining statistical tests were performed using SPSS for Windows™ (Version 14·0).

After exploring simple relationships between individual leaf traits and between leaf traits and other ecological variables, two additional more complex analyses were carried out. First, to examine how SLA varies with respect to different combinations of LDMC and LT, median values were used to divide ‘LT/LDMC space’ into quadrants, and the position of ‘SLA contours’ within this space was calculated from eqn (2a) in the Results section. Secondly, to determine the extent to which the relationship between leaf attributes and Ellenberg ‘Nitrogen Figures’ (N) changes with the typical light environment of the species, analyses of covariance (ANCOVAs) were conducted based upon groups defined by Ellenberg ‘Light Figures’ (L) using those species for which we had values for SLA, LT, LDMC and the two Ellenberg indices. In all, three ANCOVAs were performed, one for SLA, one for LT and one for LDMC, using the lm function of the R statistical package (R. Development Core Team 2008).

RESULTS

Range of values for SLA and other leaf traits

The range of values for each measured leaf trait is identified in Table 1. Perhaps significantly, our highest recorded value for SLA, 122·8 mm2 mg−1, was for the woodland herb, Ceratocapnos claviculata.

Table 1.

Range of values of specific leaf area [SLA; leaf area (mm2)/leaf mass (mg)], leaf dry matter content (LDMC, 100 × dry mass of leaf/saturated mass of leaf), leaf thickness (LT, mm) and maximum leaf size (LA, mm2) within the database

Leaf trait No. of species 5th–95th percentiles Lowest value
 Highest value
SLA 2044 7·7–40·6 2·3 Agave americana, leaf succulent 122·8 Ceratocapnos claviculata, summergreen woodland annual
LDMC 1950 9·3–38·7 4·8 Hyacinthoides × massartiana, vernal woodland geophyte with large cells 51·7 Erica multiflora, sub-shrub
Umbilicus rupestris, leaf succulent
LT 1969 0·11–0·81 0·03 Selaginella selaginoides, low-growing ‘clubmoss’ 7·5 Disphyma crassifolium, leaf succulent
LA 2015 22–17 537 1 Herniaria fruticosa, sub-shrub 946 070 Heracleum mantegazzianum, monocarpic herb
Open in a new tab

The level of correspondence between estimated LD and LDMC

Our estimate of LD explained 56 % of the variation in LDMC within the data set (Table 2; Supplementary Data Fig. S1, available online). However, LD and LDMC did not show a 1:1 relationship, and in all but one case the regression had a statistically significant constant term (Table 2). Furthermore, while LD and LDMC patterned similarly for the floras of the UK and the Canary Islands, the regression equations showed small but statistically significant differences between habitat, life history and taxonomic groupings (Table 2).

Table 2.

Correspondence for contrasted geographical, life history, habitat and taxonomic groupings between (A) estimated leaf density (LD, 100 mg mm−3) and LDMC and (B) SLA and the product of LDMC and LT

(A) LD predicting LDMC
 (B) (LDM7C × LT) predicting SLA
Grouping No. of species LD ± s.d. r2 Slope ± CI Constant ± CI r2 Slope ± CI Constant ± CI
All species 1905 22·5 ± 10·6 0·564*** 0·835 ± 0·013 0·591 ± 0·059 0·731*** –0·715 ± 0·017 1·797 ± 0·013
Region
UK 1186 23·1 ± 10·6 0·549*** 0·816 ± 0·016a 0·626 ± 0·075a 0·713*** –0·692 ± 0·020a 1·783 ± 0·015a
S Europe 793 21·9 ± 9·7 0·533*** 0·862 ± 0·022b 0·498 ± 0·096a 0·801*** –0·729 ± 0·023a 1·810 ± 0·018a
Canary Islands 124 17·8 ± 9·6 0·701*** 0·768 ± 0·040ab 0·715 ± 0·159a 0·771*** –0·703 ± 0·053a 1·783 ± 0·040a
Life history
Short-lived 778 20·6 ± 9·9 0·516*** 0·689 ± 0·017a 1·106 ± 0·077a 0·531*** –0·741 ± 0·038a 1·789 ± 0·023a
Herbaceous perennial 895 21·3 ± 9·2 0·509*** 0·848 ± 0·020b 0·579 ± 0·090b 0·737*** –0·666 ± 0·022b 1·772 ± 0·017a
Woody perennial 232 33·4 ± 11·8 0·397*** 0·766 ± 0·041c 1·208 ± 0·224a 0·791*** –0·731 ± 0·045ab 1·745 ± 0·045a
Ecological groupings
Wetland 224 20·0 ± 9·9 0·309*** 0·717 ± 0·043a 0·878 ± 0·183a 0·785*** –0·607 ± 0·037a 1·751 ± 0·025a
Woodland 215 28·8 ± 12·0 0·655*** 0·820 ± 0·033b 0·621 ± 0·170ab 0·847*** –0·848 ± 0·045b 1·855 ± 0·033b
Dryland 1248 22·6 ± 10·0 0·510*** 0·835 ± 0·016b 0·636 ± 0·074a 0·681*** –0·723 ± 0·023a 1·786 ± 0·016a
Geophytes 59 14·3 ± 5·2 0·511*** 0·903 ± 0·094b [0·144 ± 0·326b] 0·433*** –0·626 ± 0·125a 1·731 ± 0·084a
Succulents 62 10·1 ± 6·4 0·736*** 0·854 ± 0·070b 0·621 ± 0·208ab 0·680*** –0·712 ± 0·104ab 1·855 ± 0·111ab
Major taxa
Dicotyledons 1516 22·2 ± 10·5 0·609*** 0·818 ± 0·013a 0·624 ± 0·060a 0·748*** –0·754 ± 0·020a 1·799 ± 0·014a
Monocotyledons 345 23·7 ± 10·0 0·423*** 0·875 ± 0·037b 0·565 ± 0·172a 0·714*** –0·642 ± 0·034b 1·768 ± 0·028a
Open in a new tab

For clarity, the mean LD ± s.d. are values, but statistical tests were carried out using transformed data. Regression terms are given with 95 % confidence intervals (CI), and those with the same suffix are not statistically significantly different at P <0·05. Regression terms in brackets are not significantly different from zero. *** P < 0·001.

Interrelationships between SLA, LDMC, LT and LA

LDMC and LT, in separate analyses, explained 29 and 35 %, respectively of the variation in SLA within our data set (P < 0·001; n = 1914; Supplementary Data Fig. S2A, B). Moreover, because these two components of SLA were very weakly negatively correlated (R2 = 0·02; P < 0·001; n = 1858), LDMC multiplied by LT was an even more effective predictor of SLA within the full data set, explaining nearly three-quarters of the observed variation [Supplementary Data Fig. S2C; eqn (2a)].

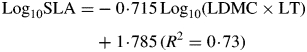graphic file with name mcr225eqn2.jpg (2a)

The corresponding equation generated for LMA, with the same level of statistical significance, was

graphic file with name mcr225eqn3.jpg (2b)

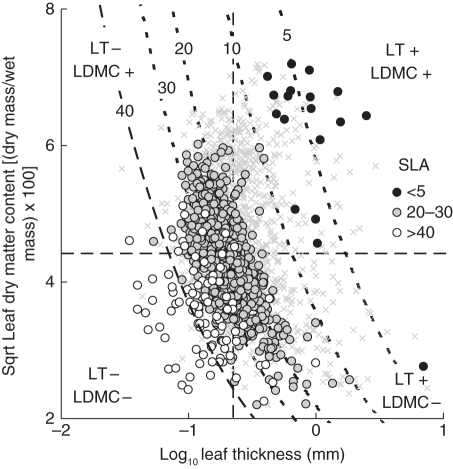
A consequence of eqn (2a) is that one value of SLA can arise from various combinations of LT and LDMC. This is illustrated by an ordination of SLA values in ‘LT/LDMC space’ (Fig. 1).

Fig. 1.

Fig. 1.

Open in a new tab

A tentative ecological classification of species (×) in relation to LT and LDMC. Median values are used to divide ‘leaf thickness/leaf dry matter content space’ (dashed lines) into quadrants and the position of five labelled ‘SLA contours’ (dotted curves) calculated from eqn (2a). Species groupings of contrasted SLA are superimposed.

The negative relationship between SLA and LDMC × LT was a consistent feature within the data set (Table 2). However, as with the relationship between LD and LDMC, the exact numeric details differed significantly between some ecological and taxonomic sub-sets (Table 2). Unlike LDMC and LT, LA was not a good predictor of SLA (Supplementary Data Fig. S2D). Only 2 % of the variation in our database was explained.

SLA, LDMC, LT and LA as predictors of RGR, leaf N and Ellenberg ‘Nitrogen Figures’

Our field-measured SLA and LDMC were both statistically significant but weak predictors of experimentally derived RGR abstracted from the scientific literature (Table 3). R2 values were slightly higher for LDMC than for SLA: Central England, LDMC R2 = 0·185, SLA R2 = 0·152 (lower by 0·032); Mediterranean succession, R2 = 0·500, SLA R2 lower by 0·280; Western European woody species, R2 = 0·270, SLA R2 lower by 0·008. Correlations between RGR and LT and LA were fewer and less consistent (Table 3). Similarly, SLA and LDMC both strongly predicted leaf N (SLA R2 = 0·412; LDMC R2 = 0·323; Table 3) but only weakly identify Ellenberg ‘Nitrogen Figures’ (SLA R2 = 0·082; LDMC R2 = 0·070; Table 3). Here, however, R2 values were slightly higher for SLA. Correlations for leaf N and Ellenberg ‘Nitrogen Figures’ with LT and LA were also highly statistically significant, but in three out of the four cases had a lower R2 than those for SLA and LDMC (leaf N, LT R2 = 0·133; LA R2 = 0·141; Ellenberg ‘Nitrogen Figures’, LT R2 = 0·018; LA R2 = 0·197; Table 3).

Table 3.

Pearson r correlations comparing relative growth rate (RGR; g g−1 d−1), leaf nitrogen content (leaf N; % dry mass of leaf) and Ellenberg ‘Nitrogen Figures’ with SLA, LDMC, LT and LA

Source of data SLA LDMC LT LA
Grime and Hunt (1975; RGRmax for flora of Central England) 0·390*** (105) –0·430*** (105) –0·046 NS (102) 0·168 P <0·1 (104)
Vile et al. (2006; RGRmax for successional species of abandoned Mediterranean farmland) 0·467* (23) –0·707*** (23) –0·088 NS (24) –0·072 NS (23)
Cornelissen et al. (1996; RGRmean for woody species from W. Europe) 0·511*** (83) –0·519*** (72) –0·342** (76) 0·279** (92)
Leaf N: NW and Mediterranean Europe (see Hodgson et al., 2005a) 0·642*** (287) –0·568*** (273) –0·364*** (280) 0·375*** (287)
Ellenberg N: C. Europe (see Ellenberg et al., 1992) 0·286*** (1105) –0·264*** (1105) –0·134*** (1105) 0·444*** (1089)
Open in a new tab

The number of species in each analysis is given in parentheses. *** P < 0·001; ** P < 0·01; * P < 0·05; NS, not significant.

Variation in LDMC, LT and SLA in relation to soil fertility and light intensity

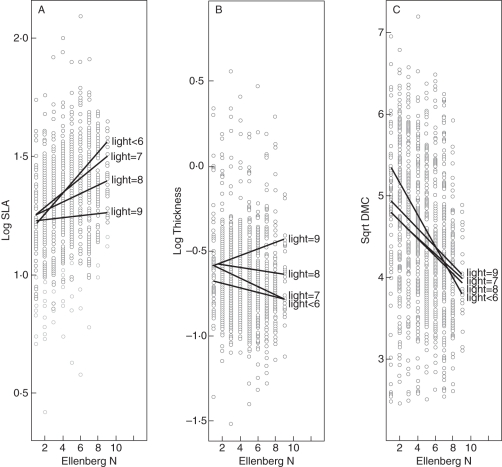
The relationship between SLA and Ellenberg ‘Nitrogen Figures’ (N) changed with the typical light environment of the species (Fig. 2A). Although log(SLA) did vary with Ellenberg N (F1,1129 = 100·35, P < 0·001) its average values also differed between the groups defined by Ellenberg L (F8,1129 = 14·22, P < 0·001). Most importantly, the slope between SLA and Ellenberg N differed significantly (F7,1084 = 3·66, P = 0·001) across the different levels of Ellenberg L. As the typical light environment of a species increased, the slope decreased (i.e. SLA increased with increasing values of Ellenberg N for species typical of shaded environments but the relationship disappeared in those species typical of the most open habitats (Fig. 2A). In contrast, in a comparable analysis using LDMC as the dependent variable (Fig. 2C), although √LDMC also varied strongly and negatively with Ellenberg N (F1,129 = 123·70, P < 0·001) and the intercepts did vary slightly with levels of Ellenberg L (F8,1129 = 2·42, P = 0·01), we detected no significant differences in the slopes across the levels of Ellenberg L (F7,1129 = 1·6, P = 0·11). In other words, as the typical level of soil fertility of a species increased, its LDMC value decreased by the same amount independently of its typical level of light intensity. With log(leaf thickness) as the dependent variable, the LT–Ellenberg N relationship was sensitive to light levels (F7,1057 = 2·85, P = 0·006) and even changed direction (Fig. 2B). At the highest light level, leaf thickness increased with increasing soil fertility but at the lower light levels leaf thickness decreased with increasing soil fertility.

Fig. 2.

Fig. 2.

Open in a new tab

Ellenberg ‘Nitrogen Figures’ plotted against (A) SLA, (B) LT and (C) LDMC for 1073 species. Lines show the linear regressions of each dependent variable against Ellenberg N for subsets of species having different Ellenberg ‘Light Figures’. Low Ellenberg figures identify extremely low concentrations of available N and deep shade, respectively, and high values identify N-rich and unshaded conditions.

DISCUSSION

Properties of the database

Since the range of values of SLA, LDMC, LT and LA in our data set were wide, the database has the ecological breadth appropriate for comparisons of functional traits. For instance, the 5th–95th percentiles for SLA (7·7–40·6 mm2 mg−1, n = 2044) were similar in range to the 3–33 recorded for the world flora (Poorter et al., 2009). Moreover, our study, with in excess of 2000 species, had the potential to identify patterns and differences that studies with fewer taxa might have failed to detect.

Differences in the expression of leaf traits between ecological and taxonomic groupings

Plants, their organs, tissues and component cells all multitask, and the leaf is no exception, being simultaneously a light collector, an energy conversion facility and a short-term energy and nutrient storage facility. Moreover, succulents have specialist water storage tissue. Furthermore, some wetland plants have aerenchyma and, even between dryland species, there is variation in the proportion of leaf air space (Niinemets, 1999; Castro-Díez et al., 2000). This will cause deviations from a strictly 1:1 relationship between LD and LDMC. Additionally, in some species, all mechanical support is provided within the tissues of the leaf itself; in others the petiole and/or stem may also contribute, generating a higher SLA and a lower LDMC than would otherwise be expected. Therefore, as emphasized by Vernescu and Ryser (2009) and Bonser et al. (2010), leaf traits do not necessarily share exact functional and structural equivalence between species.

This theoretical construct agrees with our own results. The relationship between LD and LDMC appears arithmetically inexact, but this is expected (Shipley and Vu, 2002): in consequence, that between LDMC × LT and SLA is not exact either (Table 2). Although regression equations were of the same general form for all groupings, slopes and intercepts of the set of regressions (LD vs. LDMC, and LDMC × LT vs. SLA) differed significantly for contrasted ecological and taxonomic groupings (Table 2).

In these circumstances, how valid is it to use LDMC and SLA as stand-alone ecological predictors? We urgently need to identify the extent to which the expression of other ecological factors and structural features interact with and modify the traits that we routinely use to assess soil fertility. To these ends, the studies of Garnier and Laurent (1994), Van Arendonk and Poorter (1994), Niinemets et al. (1998), Roderick et al. (1999), Vernescu and Ryser (2009) and others need to be extended so that the interrelationships between leaf structure, leaf function and trait expression are more fully understood.

Relationships between LD, LDMC, LT and SLA

For reasons identified above, traits must be used with caution in all analyses. Nevertheless, in broad-brush meta-analyses, robust statistical relationships can be identified. Although the caveats above apply, we confirm the positive relationship between LD and LDMC described by Shipley and Vu (2002). Moreover, the equivalence between LD and LDMC appears robust [see eqn (1)] because otherwise LDMC × LT could not have accounted for nearly three-quarters of the observed variation in SLA [Supplementary Data Fig. S2C; eqn (2a)]. However, the key element of our early analyses was to confirm the pioneering work of Witkowski and Lamont (1991), Wilson et al. (1999), Kitajima and Poorter (2010) and Craine and Towne (2010), who all identified that SLA is a compound trait, a function of LDMC and LT. As a result of this duality, species differing markedly in leaf form and function can have the same SLA value (see Vernescu and Ryser, 2009) and, as illustrated in Fig. 1, very different combinations of LT and LDMC regularly generate similar values of SLA. Moreover, in a paper on the leaves of tropical trees, Kitajima and Poorter (2010) identified variation in dry mass density and tissue level mechanical strength as loading strongly on principal component analysis (PCA) axis 1 (with LDMC as a component variable) while lamina thickness loaded strongly on PCA axis 2. SLA (as LMA) was an important component of both axes. In summary, and as illustrated from a more physiological viewpoint by Niinemets (1999), SLA is a compound trait responding to two underlying traits (LD and LT) that have different functional roles.

The origins of SLA's popularity

That SLA is a function of LDMC and LT was already well established (Witkowski and Lamont, 1991) before SLA became the ecological trait of choice for identifying soil fertility. So, where does this popularity of SLA originate? We suspect that the key reason has been historical inertia. RGRmax was considered a key indicator of soil fertility (i.e. ‘stress’) by Grime (1979), but RGR is difficult and time-consuming to measure. However, the classical decomposition of RGR [eqn (3); see, for example, Evans, 1972)] shows that it is partly a function of SLA, an easily measured variable that does not require sequential harvests.

graphic file with name mcr225eqn4.jpg (3)

where RGR, NAR and LMF are relative growth rate (g g−1 d−1), net assimilation rate (or unit leaf rate; g cm−2 d−1) and leaf mass fraction (g g−1), respectively: this equation, used routinely in growth analysis, equates to eqn (1c) in Shipley (2006) and is similarly expressed in Poorter et al. (2009).

Tilman's (1988) influential book identified biomass allocation to leaves as a key determinant of RGR, and RGR was then found to be tightly correlated with SLA in the pioneering interspecific study of Poorter and Remkes (1990). Furthermore, although Shipley (2002) found otherwise, SLA has been identified as more important than NAR as a predictor of RGR (Poorter and Remkes, 1990; Poorter and van der Werf, 1998; Veneklaas and Poorter, 1998). SLA is also regarded as a key element of the ‘worldwide leaf economics spectrum’ of Wright et al. (2004). Thus, SLA appeared to ‘have it all’. Not only was it a key determinant of growth rate in the laboratory, but SLA also defined crucial ecosystem processes in the field. This view, that SLA was an effective stand-alone predictor of soil fertility and growth rate, was formalized within the LHS plant ecology strategy scheme of Westoby (1998).

Casting a shadow over SLA

From the outset, the potential impacts of shade (and its LT component) on the expression of SLA have not been adequately assessed. In the case of growth analysis, there were at first technical constraints. The best artificial lighting available provided only low irradiance, and many early experiments were effectively carried out in shaded conditions. For example, the classic ecological growth rate study of the British flora (Grime and Hunt, 1975) was performed at only ‘24 % of the mean daily value for similar latitudes to Sheffield’, while Poorter and Remkes (1990) used only 300 µmol photons m−2 s−1. In this context, it may be significant that the strength of the relationship between RGR and SLA appears to decline at higher light intensities (Poorter, 1999; Shipley, 2006), where, coincidently, the interspecific range of LT is likely to be greater. If light intensities had been uniformly higher in all early work, the possible impact of LT on the expression of growth rate may have been more fully explored with the ‘classic’ eqn (3) recast as

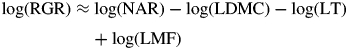graphic file with name mcr225eqn5.jpg (4)

Superimposed upon this technical problem in relation to growth rate has been an ecological one. Species of deep shade typically constitute only a small fraction of the total flora (e.g. in Ellenberg et al., 1992) and have generally been poorly represented in ecological studies. Often, therefore, impacts of shade on the expression of SLA are not immediately apparent. Take, for example, Table 3, where a similar capacity to predict Ellenberg N was identified for both SLA and LDMC. When the typical light environment of each species was factored into the analysis, this broad equivalence disappeared. A typical light environment was now identified as an important co-variant (Fig. 2). The relationship of SLA with Ellenberg N changed with the typical light environment of the species (Fig. 2A). As a result, SLA became clearly identified as a flawed predictor of soil fertility. This failure of SLA was because one of its component variables, LT, is in many respects a shade index (Fig. 2B). In contrast, since it was negatively correlated with Ellenberg N and did not change with the typical light environment of the species (Fig. 2C), LDMC was the better, more consistent predictor of soil fertility.

CONCLUSIONS

SLA appears to be a hybrid ‘soil fertility–shade’ index. In open habitats with lower above-ground biomass and less shading within the canopy, it may predict, as it is supposed to, soil fertility and position in the ‘worldwide leaf economics spectrum’ of Wright et al. (2004). On the other hand, in productive sites with higher biomass and canopy density, there may be an additional elevation of the SLA value because of the presence of inherently thin-leaved, more shade-tolerant species. Such species are not just low-growing subordinates. Often, they are major contributors to the biomass: canopy dominants typically possess several overlapping layers of leaves and there is potentially a high degree of self-shading (see Niinemets, 2007). It appears that leaf morphological plasticity plays a more important role in determining foliar adaptation to high irradiance, whereas at low light biochemical and anatomical changes are of similar magnitude (Niinemets et al., 1998). In this context, we urgently need to identify the point of inflection where high SLA ceases to identify the potential for fast growth and high biomass accumulation but begins instead to signify slow growth under chronically light-deficient conditions. Until this has been achieved, there is a strong case for the additional use of an independent index of shade tolerance to make the prediction of soil fertility using leaf traits less ambiguous.

The ‘worldwide leaf economics spectrum’ of Wright et al. (2004) was identified using multivariate analyses. It will robustly inform ecologists for many years to come. However, the ideal, a predictor of soil fertility that works in all field situations, is problematic. Traits do not necessarily exhibit an exact functional equivalence between taxa (see Stebbins, 1974; Bonser et al., 2010), or even necessarily between habitats. Therefore, rather than a stand-alone, ‘flag-ship’ predictive trait, multivariate analysis of trait matrices, with SLA included (e.g. Jones et al., 2000; Hodgson et al., 2005a, b), is perhaps the best way forward. In the event of limited availability of data, we strongly recommend that the advice of Wilson et al. (1999) is followed. Rather than SLA, LDMC, whose link with growth rate and soil fertility is less ambiguously identified, should be the preferred predictive trait in studies relating to soil fertility.

SUPPLEMENTARY DATA

Supplementary data are available online at www.aob.oxfordjournals.org and consist of the folowing. Figure S1: leaf density (LD) predicts leaf dry matter content (LDMC). Figure S2: leaf dry matter content (LDMC), leaf thickness (LT), leaf dry matter content × leaf thickness and leaf size (LA) as predictors of specific leaf area (SLA).

Supplementary Data
supp_108_7_1337__index.html (925B, html)

ACKNOWLEDGEMENTS

A considerable quantity of the data used in this project was collected during projects funded by NERC (UK) and Comisión Interministerial de Ciencia y Tecnología (Spain). We thank Phil Grime, Simon Pierce, Bill Smith and two anonymous reviewers for constructive criticism of an earlier version of this manuscript.

LITERATURE CITED

  1. Bolhàr-Nordenkampf HR, Draxler G. Functional leaf anatomy. In: Hall DO, Scurlock JMO, Bolhàr-Nordenkampf HR, Leegood RC, Long SP, editors. Photosynthesis and production in a changing environment: a field and laboratory manual. London: Chapman and Hall; 1993. pp. 91–112. [Google Scholar]
  2. Bonser SP, Ladd B, Monro K, et al. The adaptive value of functional and life-history traits across fertility treatments in an annual plant. Annals of Botany. 2010;6:979–988. doi: 10.1093/aob/mcq195. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Castro-Díez P, Puyravaud JP, Cornelissen JHC. Leaf structure and anatomy as related to leaf mass per area variation in seedlings of a wide range of woody plant species and types. Oecologia. 2000;124:476–486. doi: 10.1007/PL00008873. [DOI] [PubMed] [Google Scholar]
  4. Charles M, Jones G, Hodgson JG. FIBS in Archaeobotany: functional interpretation of weed floras in relation to husbandry practices. Journal of Archaeological Science. 1997;24:1151–1161. [Google Scholar]
  5. Cornelissen JHC. Seasonal and year to year variation in performance of Gordonia acuminata seedlings in different light environments. Canadian Journal of Botany. 1992;70:2405–2414. [Google Scholar]
  6. Cornelissen JHC, Castro-Díez P, Hunt R. Seedling growth, allocation and leaf attributes in a wide range of woody plant species and types. Journal of Ecology. 1996;84:755–765. [Google Scholar]
  7. Cornelissen JHC, Lavorel S, Garnier E, et al. A handbook of protocols for standardized and easy measurement of plant functional traits worldwide. Australian Journal of Botany. 2003;51:335–380. [Google Scholar]
  8. Craine JM, Towne EG. High leaf tissue density grassland species consistently more abundant across topographic and disturbance contrasts in a North American tallgrass prairie. Plant and Soil. 2010;337:193–203. [Google Scholar]
  9. De Frenne P, Graae BJ, Kolb A, et al. An intraspecific application of the leaf–height–seed ecology strategy scheme to forest herbs along a latitudinal gradient. Ecography. 2011;34:132–140. [Google Scholar]
  10. Díaz S, Hodgson JG, Thompson K, et al. The plant traits that drive ecosystems: evidence from three continents. Journal of Vegetation Science. 2004;15:295–304. [Google Scholar]
  11. Dong M. Morphological plasticity of the clonal herb Lamiastrum galeobdelon (L.) Ehrend& Polateschek in response to partial shading. New Phytologist. 1993;124:291–300. doi: 10.1111/j.1469-8137.1993.tb03819.x. [DOI] [PubMed] [Google Scholar]
  12. Ellenberg H, Weber HE, Dull R. Zeigwerte von Pflanzen in Mitteleuropa. Scripta Geobotanica. ((2nd edn.)) 1992;18:1–258. [Google Scholar]
  13. Evans GC. The quantitative analysis of plant growth. Oxford: Blackwell; 1972. [Google Scholar]
  14. Garnier E, Laurent G. Leaf anatomy, specific mass and water content in congeneric annual and perennial grass species. New Phytologist. 1994;128:725–736. [Google Scholar]
  15. Garnier E, Shipley B, Roumet C, Laurent G. A standardized protocol for the determination of specific leaf area and leaf dry matter content. Functional Ecology. 2001;15:688–695. [Google Scholar]
  16. Givnish TJ. Biomechanical constraints on crown geometry in forest herbs. In: Givnish TJ, editor. On the economy of plant form and function. Cambridge: Cambridge University Press; 1976. pp. 525–583. [Google Scholar]
  17. Grime JP. Plant strategies, vegetation processes and ecosystem properties. Chichester: John Wiley & Sons; 1979. [Google Scholar]
  18. Grime JP, Hunt R. Relative growth-rate: its range and adaptive significance in a local flora. Journal of Ecology. 1975;63:393–422. [Google Scholar]
  19. Grime JP, Thompson K, Hunt R, et al. Integrated screening validates primary axes of specialisation in plants. Oikos. 1997;79:259–281. [Google Scholar]
  20. Grime JP, Hodgson JG, Hunt R. Comparative plant ecology. 2nd edn. Dalbeattie, UK: Castlepoint Press; 2007. [Google Scholar]
  21. Hodgson JG, Montserrat-Martí G, Cerabolini B, et al. A functional method for classifying European grasslands for use in joint ecological and economic studies. Basic and Applied Ecology. 2005a;6:119–131. [Google Scholar]
  22. Hodgson JG, Montserrat-Martí G, Tallowin J, et al. How much will it cost to save grassland diversity? Biological Conservation. 2005b;122:263–273. [Google Scholar]
  23. Hodgson JG, Sharafi M, Jalili A, et al. Stomatal vs. genome size in angiosperms: the somatic tail wagging the genomic dog? Annals of Botany. 2010;105:573–584. doi: 10.1093/aob/mcq011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Jones G, Bogaard A, Charles M, Hodgson JG. Distinguishing the effects of agricultural practices relating to fertility and disturbance: a functional ecological approach in archaeobotany. Journal of Archaeological Science. 2000;27:1073–1084. [Google Scholar]
  25. Kitajima K, Poorter L. Tissue-level leaf toughness, but not lamina thickness, predicts sapling leaf lifespan and shade tolerance of tropical tree species. New Phytologist. 2010;186:708–721. doi: 10.1111/j.1469-8137.2010.03212.x. [DOI] [PubMed] [Google Scholar]
  26. Kleyer M, Bekker RM, Knevel IC, et al. The LEDA Traitbase: a database of life-history traits of the Northwest European flora. Journal of Ecology. 2008;96:1266–1274. [Google Scholar]
  27. Lambers H, Poorter H. Inherent variation in growth rate between higher plants: a search for physiological causes and ecological consequences. Advances in Ecological Research. 1992;23:187–261. [Google Scholar]
  28. Laughlin DC, Leppert JJ, Moore MM, Sieg CH. A multi-trait test of the leaf–height–seed plant strategy scheme with 133 species from a pine forest flora. Functional Ecology. 2010;24:493–501. [Google Scholar]
  29. Lusk CH, Reich PB, Montgomery RA, Ackerly DD, Cavender-Bares J. Why are evergreen leaves so contrary about shade? Trends in Ecology and Evolution. 2008;23:299–303. doi: 10.1016/j.tree.2008.02.006. [DOI] [PubMed] [Google Scholar]
  30. Niinemets Ü. Components of leaf dry mass per area – thickness and density – alter leaf photosynthetic capacity in reverse directions in woody plants. New Phytologist. 1999;144:35–47. [Google Scholar]
  31. Niinemets Ü. Photosynthesis and resource distribution through plant canopies. Plant, Cell and Environment. 2007;30:1052–1071. doi: 10.1111/j.1365-3040.2007.01683.x. [DOI] [PubMed] [Google Scholar]
  32. Niinemets Ü, Kull O, Tenhunen JD. An analysis of light effects on foliar morphology, physiology, and light interception in temperate deciduous woody species of contrasting shade tolerance. Tree Physiology. 1998;18:681–696. doi: 10.1093/treephys/18.10.681. [DOI] [PubMed] [Google Scholar]
  33. Niinemets Ü, Portsmuth A, Tena D, et al. Do we underestimate the importance of leaf size in plant economics? Disproportional scaling of support costs within the spectrum of leaf physiognomy. Annals of Botany. 2007;100:283–303. doi: 10.1093/aob/mcm107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Poorter H, Remkes C. Leaf area ratio and net assimilation rates of 24 species differing in relative growth rate. Oecologia. 1990;83:553–559. doi: 10.1007/BF00317209. [DOI] [PubMed] [Google Scholar]
  35. Poorter H, van der Werf A. Is inherent variation in RGR determined by LAR at low irradiance and by NAR at high irradiance? A review of herbaceous species. In: Lambers H, Poorter H, van Vuuren MMI, editors. Inherent variation in plant growth, physiological mechanisms and ecological consequences. Leiden, The Netherlands: Backhuys Publishers; 1998. pp. 309–336. [Google Scholar]
  36. Poorter H, Niinemets Ü, Poorter L, Wright IJ, Villar R. Causes and consequences of variation in leaf mass per area (LMA): a meta-analysis. New Phytologist. 2009;182:565–588. doi: 10.1111/j.1469-8137.2009.02830.x. [DOI] [PubMed] [Google Scholar]
  37. Poorter L. Growth responses of 15 rain forest tree species to a light gradient: the relative importance of morphological and physiological traits. Functional Ecology. 1999;13:396–410. [Google Scholar]
  38. Popma J, Bongers F. The effect of canopy gaps on the growth and morphology of seedlings of rain forest species. Oecologia. 1988;75:625–632. doi: 10.1007/BF00776429. [DOI] [PubMed] [Google Scholar]
  39. R Development Core Team. R: a language and environment for statistical computing. Vienna: R Foundation for Statistical Computing; 2008. http://www.r-project.org . [Google Scholar]
  40. Reich PB, Walters MB, Ellsworth DS. Leaf life-span in relation to leaf plant and stand characteristics among diverse ecosystems. Ecological Monographs. 1992;62:365–392. [Google Scholar]
  41. Roderick ML, Berry SL, Saunders AR, Noble IR. On the relationship between the composition, morphology and function of leaves. Functional Ecology. 1999;13:696–710. [Google Scholar]
  42. Royo Pla F. Flora i vegetació de les planes i serres litorials compreses entre el riu Ebro i la serra d'Irta. Barcelona: PhD thesis, Universitat de Barcelona; 2006. [Google Scholar]
  43. Schaffers AP, Sykora KV. Reliability of Ellenberg indicator values for moisture, nitrogen and soil reaction: a comparison with field measurements. Journal of Vegetation Science. 2000;11:225–244. [Google Scholar]
  44. Shipley B. Trade-offs between net assimilation rate and specific leaf area in determining relative growth rate: relationship with daily irradiance. Functional Ecology. 2002;16:682–689. [Google Scholar]
  45. Shipley B. Net assimilation rate, specific leaf area and leaf mass ratio: which is most closely correlated with relative growth rate? A meta-analysis. Functional Ecology. 2006;20:565–574. [Google Scholar]
  46. Shipley B, Vu T-T. Dry matter content as a measure of dry matter concentration in plants and their parts. New Phytologist. 2002;153:359–364. [Google Scholar]
  47. Shipley B, Lechowicz MJ, Wright I, Reich PB. Fundamental trade-offs generating the worldwide leaf economics spectrum. Ecology. 2006;87:535–541. doi: 10.1890/05-1051. [DOI] [PubMed] [Google Scholar]
  48. Stace CA. New Flora of the British Isles. 2nd edn. Cambridge: Cambridge University Press; 1997. [Google Scholar]
  49. Stebbins GL. Flowering plants: evolution above the species level. Cambridge, MA: Belknap Press; 1974. [Google Scholar]
  50. Terashima I, Miyakawa S-I, Hanbe YT. Why are sun leaves thicker than shade leaves? Consideration based on analyses of CO2 diffusion in the leaf. Journal of Plant Research. 2001;114:93–105. [Google Scholar]
  51. Thompson K, Hodgson JG, Grime JP, et al. Ellenberg numbers revisited. Phytocoenologia. 1993;89:277–289. [Google Scholar]
  52. Thompson K, Parkinson JA, Band SR, Spencer RE. A comparative study of leaf nutrient concentrations in a regional herbaceous flora. New Phytologist. 1997;136:679–689. doi: 10.1046/j.1469-8137.1997.00787.x. [DOI] [PubMed] [Google Scholar]
  53. Tilman D. Plant strategies and the dynamics and structure of plant communities. Monographs in population biology 26. Princeton, NJ: Princeton University Press; 1988. [Google Scholar]
  54. Tutin TG, Heywood VH, Burges NA, et al. Flora Europaea vols 1–5. Cambridge: Cambridge University Press; 1964–1980. [Google Scholar]
  55. Van Arendonk JJCM, Poorter H. The chemical composition and anatomical structure of leaves of grass species differing in relative growth rate. Plant, Cell and Environment. 1994;17:963–970. [Google Scholar]
  56. Vendramini F, Diaz S, Gurvich DE, et al. Leaf traits as indicators of resource-use strategy in floras with succulent species. New Phytologist. 2002;154:147–157. [Google Scholar]
  57. Veneklaas EJ, Poorter L. Carbon partitioning strategies of tropical tree seedlings in contrasting light environments. In: Lambers H, Poorter H, van Vuuren MMI, editors. Inherent variation in plant growth, physiological mechanisms and ecological consequences. Leiden, The Netherlands: Backhuys Publishers; 1998. pp. 337–361. [Google Scholar]
  58. Vernescu C, Ryser P. Constraints on leaf structural traits in wetland plants. American Journal of Botany. 2009;96:1068–1074. doi: 10.3732/ajb.0800312. [DOI] [PubMed] [Google Scholar]
  59. Vile D, Garnier E, Shipley B, et al. Specific leaf area and dry matter content estimate thickness in laminar leaves. Annals of Botany. 2005;96:1129–1136. doi: 10.1093/aob/mci264. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Vile D, Shipley B, Garnier E. Ecosystem productivity can be predicted from potential relative growth rate and species abundance. Ecology Letters. 2006;9:1061–1067. doi: 10.1111/j.1461-0248.2006.00958.x. [DOI] [PubMed] [Google Scholar]
  61. Warton DL, Wright IJ, Falster DS, Westoby M. Bivariate line-fitting methods for allometry. Biological Reviews. 2006;81:259–291. doi: 10.1017/S1464793106007007. [DOI] [PubMed] [Google Scholar]
  62. Westoby M. A leaf–height–seed (LHS) plant ecology strategy scheme. Plant and Soil. 1998;199:213–227. [Google Scholar]
  63. Wilson PJ, Thompson K, Hodgson JG. Specific leaf area and leaf dry matter content as alternative predictors of plant strategies. New Phytologist. 1999;143:155–162. [Google Scholar]
  64. Witkowski ETF, Lamont BB. Leaf specific mass confounds leaf density and thickness. Oecologia. 1991;88:486–493. doi: 10.1007/BF00317710. [DOI] [PubMed] [Google Scholar]
  65. Wright IJ, Reich PB, Westoby M, et al. The worldwide leaf economics spectrum. Nature. 2004;428:821–827. doi: 10.1038/nature02403. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
supp_108_7_1337__index.html (925B, html)
supp_mcr225_mcr225supp.pdf (401.4KB, pdf)

Articles from Annals of Botany are provided here courtesy of Oxford University Press

RESOURCES