Figure 2.

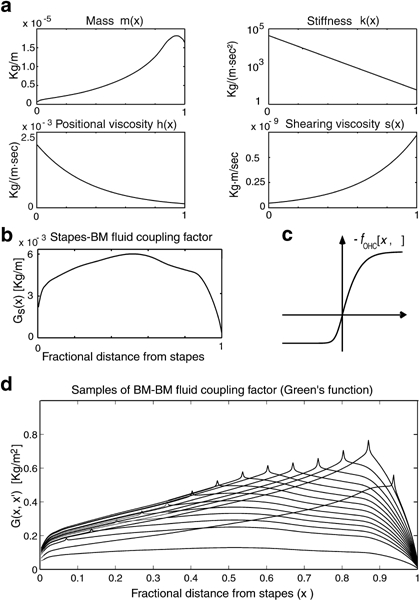
Graphic representation of basilar membrane (BM) distributed parameters for the human cochlea model. a.m(x) is mass, k(x) is stiffness, h(x) is positional viscosity, and s(x) is shearing viscosity. All parameters plotted versus normalized longitudinal position (x) on the BM. b. Profile of stapes–BM fluid coupling factor G_S(x) representing the downward force sensed by the unit BM segment centered at the BM site x under the action of unit inward stapes acceleration [Eq. (A3)]; G_S(x) also represents the outward force sensed by the stapes under unit BM upward acceleration [Eq. (1)]. c. Sigmoid profile representing the outer hair cell (OHC) motor force as −f_OHC(x,η) vs. stereocilia deflection η [Eq. (A3)]. d. Green’s function G(x,x′) representing the BM–BM fluid coupling factor, i.e., the downward force sensed by the unit BM segment centered at the BM site x, under the action of unit upward acceleration of the unit BM segment at x′. G(x, x′) enters as a positive-definite (x ↔ x′) symmetric kernel in the BM motion Eq. (A3). Spikes should be understood as logarithmic singularities of G(x, x′) at x =x′ (Allen 1977). G_S(x) and G(x, x′) were determined using spiral canal geometry, BM width, and stapes area for the human cochlea (Zwislocki–Mościcki 1948; Fernàndez 1952) following the computational procedure described in Mammano and Nobili (1993).