Toward a General Model for the Evolutionary Dynamics of Gene Duplicates

Abstract

Gene duplication is an important process in the functional divergence of genes and genomes. Several processes have been described that lead to duplicate gene retention over different timescales after both smaller-scale events and whole-genome duplication, including neofunctionalization, subfunctionalization, and dosage balance. Two common modes of duplicate gene loss include nonfunctionalization and loss due to population dynamics (failed fixation). Previous work has characterized expectations of duplicate gene retention under the neofunctionalization and subfunctionalization models. Here, that work is extended to dosage balance using simulations. A general model for duplicate gene loss/retention is then presented that is capable of fitting expectations under the different models, is defined at t = 0, and decays to an orthologous asymptotic rate rather than zero, based upon a modified Weibull hazard function. The model in a maximum likelihood framework shows the property of identifiability, recovering the evolutionary mechanism and parameters of simulation. This model is also capable of recovering the evolutionary mechanism of simulation from data generated using an unrelated network population genetic model. Lastly, the general model is applied as part of a mixture model to recent gene duplicates from the Oikopleura dioica genome, suggesting that neofunctionalization may be an important process leading to duplicate gene retention in that organism.

Introduction

Gene duplication has been identified as a major driving force in structural and functional genome evolution (Roth et al. 2007). Gene duplication events are mutational events occurring in a single individual within a population. The duplication events occur through transposition events and through various other events leading to segmental, whole-chromosome, or whole-genome duplication (Zhang 2003; Hurles 2004). The subsequent mutational events in conjunction with the structure and function of genes involved in the duplication process then dictate the fate of the gene duplicate. For single-gene duplications, the possible fates of any gene duplicate are non-, neo-, and subfunctionalization (Dittmar and Liberles 2010; Innan and Kondrashov 2010). The original function could also be retained due to selection for robustness or increased dosage. However, for duplication events that include a number of interacting genes, dosage balance constraints impose selective pressure on individual gene retention and loss (Hughes et al. 2007).

Individual genes can have a number of different functions and structures that affect their likelihood of becoming nonfunctionalized, gaining a function (neofunctionalization), becoming subfunctionalized (Hughes 1994; Force et al. 1999; Lynch et al. 2001), or retaining function. In general, a eukaryotic gene consists of multiple locations that can differentially evolve after gene duplication, including splice sites in introns (Tarrío et al. 1998; Lin et al. 2006), coding region sequence (exons) (Gu et al. 2002; Conant and Wagner 2003; Makova and Li 2003; Li et al. 2005), exon number (Kondrashov and Koonin 2001; Letunic et al. 2002; Zhang et al. 2009), the core promoter with transcription factor–binding and transcription start sites (Reece-Hoyes et al. 2007), enhancers (Kay et al. 1987; Panavas et al. 2003), silencers (Hickman and Rusche 2010), insulators (Dorer and Henikoff 1994), untranslated regions (D'Souza et al. 2004; Rogers et al. 2004), and multiple other regulatory elements necessary for proper function and expression (Lee and Young 2000; Lynch 2006). Depending on the location of mutations, the gene duplicate can be affected differently, with the probabilities of affecting each type of element dictated by the number of sites that can accommodate change and differentially affect function (Liberles et al. 2010).

Nonfunctionalization refers to the loss of all functionality of a gene and is accepted as the most common fate post-duplication (Lynch and Conery 2000). For example, if a given gene has a single function where its protein product interacts with one substrate through one binding site, is expressed in a single tissue, and has no alternative splice variants, then a knockout of that binding site, any essential site necessary for proper folding, or any essential regulatory element will lead to the non- (or pseudo-) functionalization of that gene duplicate. Nonfunctionalization is different from the population genetic-driven loss that can occur without mutation post-duplication (Lynch et al. 2001). Whereas population genetic loss refers to a failure of the duplicate to fix or continue to segregate in the population, nonfunctionalization leaves behind a pseudogenized gene in the genome in at least a fraction of individuals (Zheng and Gerstein 2007; Zhang et al. 2008).

The neofunctionalization model was popularized as a theory explaining evolutionary sources of novel protein function (Ohno 1970) but can also apply to the level, timing, or localization of gene expression (Innan and Kondrashov 2010).

Subfunctionalization involves complementary loss and retention of individually acting subfunctions between the gene copies, leading to the need of retaining both, so that all essential ancestral functions of the gene are conserved between the duplicate pair (Hughes 1994; Force et al. 1999). This loss of function within the genes is generally mediated by nonfunctionalization of regulatory elements (tissue or developmentally specific), splice sites, or mutations in the coding region, which are specific to individual subfunctions. The probability of subfunctionalization increases with the number of subfunctions in the gene under consideration (Lynch and Force 2000). If the duplicated gene has multiple splice variants with different binding interactions and knockouts of different splice sites between the two duplicates occur, then the result would be subfunctionalization of the duplicates with the ultimate retention of both. The same is true for complementary loss of different tissue-specific regulatory elements between the two gene copies or differential loss of interaction at distinct binding sites on the protein surface (Hughes 1994; Force et al. 1999; Liu and Adams 2010).

In addition to the processes acting on individual genes described above, large-scale gene duplication (segmental, whole chromosome, and whole genome) events duplicate multiple interacting genes together creating an additional retention mechanism (Papp et al. 2003; Aury et al. 2006; Hughes et al. 2007). Dosage balance promotes the retention of duplicated interaction networks as loss of individual parts of the interaction network can lead to declines in fitness. However, if only individual genes within the network are duplicated, dosage balance promotes loss or nonfixation in order to prevent imbalance within the ancestral interaction network (Veitia et al. 2008; Edger and Pires 2009; Freeling 2009). This is also observed in genes on sex chromosomes, where mechanisms to account for differences in expression between males and females have evolved in some but not all species (Walters and Hardcastle 2011). The theory behind the dosage balance model explains the retention of entire gene networks post–large-scale duplications due to stoichiometric balance constraints pre- and postduplication (Veitia et al. 2008). Dosage imbalance involves changes in protein concentrations relative to those of potential binding partners, potentially resulting in improper protein complex assembly (Veitia 2002), spurious interactions (Liberles et al. 2011), and deleterious downstream effects on pathways. On the other hand, network duplication can affect the fitness of an organism by increasing its energy needs as more genetic material needs to be transcribed and translated at energetic cost (Wagner 2005).

In terms of genome evolution, non-, neo-, and subfunctionalization and dosage balance are not exclusive of one another (He and Zhang 2005; Rastogi and Liberles 2005). One would expect all duplicates under stoichiometric constraints to be retained for long evolutionary timescales before duplicates are cooperatively lost (Hughes et al. 2007). Thus, dosage balance may in fact be acting as an intermediate step to neo-and subfunctionalization, prolonging the retention of the duplicates before one of the other mechanisms determines the ultimate fate of the duplicates (Hughes et al. 2007). In dosage-compensated duplicates, network interactions can be lost through nonfunctionalization of entire genes or through loss of individual interactions, which when lost complementarily will result in subfunctionalization.

Models for gene duplicate retention enable insight into the evolution of protein function following speciation and lineage-specific evolution. Most genome sequencing studies include a pairwise analysis of recent duplicates and models of gene duplication are increasingly utilized to characterize the average properties of synonymous substitution rate (dS)-dependent duplicate gene retention (Lynch and Conery 2000, 2003; Aury et al. 2006; Hughes and Liberles 2007, 2008a; Denoeud et al. 2010). This gives an insight into the retention of duplicates under different-scale gene/genome duplication events (Maere et al. 2005; Blomme et al. 2006; Hughes and Liberles 2007, 2008a, 2008b) and provides the basis for understanding and modeling gene retention. After large-scale duplications, it has been shown that certain biochemical functions of some genes lead to preferential retention over others and that a larger proportion of duplicates are retained than after small-scale duplication (Blomme et al. 2006). Hughes and Liberles (2008a) illustrated that the size distribution of gene families can be explained by heterogeneity of loss rates between families, which further confirmed the differential retention between genes of certain functions after large- and small-scale duplications (Maere et al. 2005). This led to the conclusion that no single description of loss rates can be applied to duplicate loss for both large- and small-scale duplications but rather that the loss processes after different-scale duplications have to be addressed independently (Maere et al. 2005; Hughes and Liberles 2008b). In order to do so, loss functions have to be described for neo- and subfunctionalization, as well as dosage balance.

The previously discussed models of gene retention can be applied to the orthology/paralogy problem, as well as the problem of gene tree/species tree reconciliation. Currently, most phylogenetic approaches used for gene tree/species tree reconciliation, inference of gene duplications and losses, and orthology/paralogy identification have been based on parsimony approaches such as Softparsmap (Berglund-Sonnhammer et al. 2006) and Notung (Chen et al. 2000) and on distance methods, such as Orthostrapper (Storm and Sonnhammer 2002). Even without considering mechanistic complexity, most parsimonious reconciliations will be subject to the same limitations as parsimony-based approaches in sequence-based phylogenetics (Nielsen 2002) and models are needed. Gene duplication and loss has been modeled using a relatively simple birth–death process (Liu and Pearl 2007; Arvestad et al. 2009; Rasmussen and Kellis 2011). The simplest biological birth–death model is based upon an exponential distribution that assumes that the rate of loss (hazard) of a duplicated gene is constant through time and is based on earlier work by Lynch and Conery (2000, 2003). This expectation is consistent with the nonfunctionalization process but does not take into account any of the processes of retention discussed previously. Further, not only is the exponential loss model exclusively consistent with a constant neutral rate of loss but it also decays to zero (where all duplicates are lost) and is not defined at t = 0, the point of duplication.

In order to expand this birth–death process to include the processes of neofunctionalization, subfunctionalization, and dosage balance, the hazard or loss rate function for these processes has to be characterized. Hughes and Liberles (2007) and Zhang et al. (2004) illustrated that the neofunctionalization hazard rate (instantaneous rate of duplicate copy loss) declines with time. Once a gene duplicate is neofunctionalized, the nonfunctionalization probability for this duplicate declines, leading to the overall decline of duplicate loss over long evolutionary time periods. This convexly declining loss rate has been described with a Weibull hazard function (Hughes and Liberles 2007). Further, the subfunctionalization loss rate behavior has been characterized to be concavely declining (Hughes and Liberles 2007) based upon theoretical expectations of a waiting time for complementary mutations (Force et al. 1999; Lynch et al. 2001; Hughes and Liberles 2007). The hazard function for dosage balance has not yet been characterized quantitatively. However, the theoretical expectations under this model are an initial very low loss rate over prolonged evolutionary time (due to negative selective constraints on dosage imbalance caused by individual link or gene loss), with a rapid increase due to cooperative loss once the first loss of any one gene duplicate in the network approaches fixation (Hughes et al. 2007), resulting in a concavely increasing hazard rate.

These differences in the hazard functions between models have to be taken into account when using a birth–death process for modeling duplicate retention. This can be modeled by a flexible hazard function, which, under different parameterizations, is consistent with any of the given underlying mechanisms. The function can simply be combined in a mixture model for data covering multiple events, where the number of components of the mixture is determined statistically in either a Bayesian or a maximum likelihood framework. Further, because duplicate genes exist at t = 0, a model defined at t = 0 is necessary.

The basic features of the model are the hazard shapes seen in figure 2. Nonfunctionalization as a neutral process involves a flat hazard function with a constant neutral rate of gene loss. Neofunctionalization involves a weighting time for a single advantageous change, characterized by a convexly declining hazard function. Subfunctionalization involves a weighting time for two complementary changes with an increased period at the neutral loss rate, resulting in a concavely declining hazard function. Dosage balance results in a convexly increasing hazard function when balance is lost stochastically. Generalizations to the Weibull distribution have been previously developed (e.g., Mudholkar et al. 1996), but a new flexible distribution based upon a Weibull-like hazard function was developed with the above properties.

FIG. 2.—

The hazard function (left) and corresponding survival function (right) for duplicated gene retention under different theoretical models is shown. Nonfunctionalization has a flat hazard, whereas neofunctionalization a concavely declining hazard, subfunctionalization a convexly declining hazard, and dosage balance a concavely increasing hazard. The figure is only illustrative, and different parameterizations with each mechanism will give variations on the curve shapes, including the timescale of action.

Here, we characterize the behavior of dosage balance–mediated duplicate retention and loss rates via simulations, allowing for different link and gene loss probabilities, population sizes, and gene network size. Due to the potential effect of subfunctionalization, we investigate the duplicate loss behavior under three different models. One model allows for subfunctionalization in addition to dosage balance (consistent with a protein interacting with its different binding partners at different times), whereas a second excludes subfunctionalization (consistent with a protein that functions in a complex). A third model builds upon previous characterization of neofunctionalization (Hughes and Liberles 2007), considering this process in combination with dosage balance.

Finally, we combine our findings of the hazard function under dosage balance with the previous studies of non-, neo-, and subfunctionalization and introduce a generalized mathematical model that can explain the trends of duplicate retention under all discussed models. Lastly, this mixture model is applied to characterize patterns of duplicate gene retention in the Oikopleura dioica genome.

Materials and Methods

Simulations of Dosage Balance Gene Retention

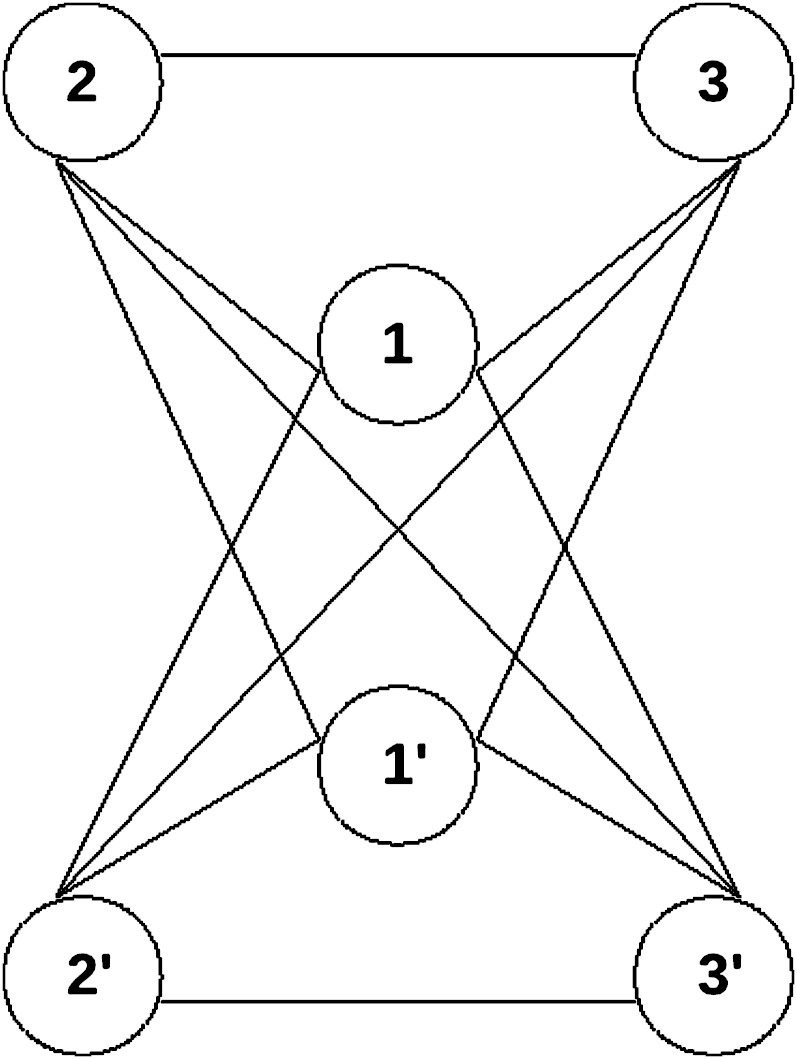
A network of varying size (three to five members) was constructed, where each protein product interacts with all other protein products immediately after duplication, except its own duplicate (fig. 1). Simulations on this network were run for 2,000 generations with population sizes of 100 and 1,000 individuals following an initial whole-genome duplication event. Both entire genes as well as individual links can be lost during any given generation with the probability of losing a gene Pr(lose gene) and the probability of losing a link Pr(lose link). Losing an entire gene refers to the simultaneous loss of all its links to all other genes. Loss of individual links during the simulation refers to loss of regulatory or structural elements that affects particular subfunctions of the gene rather than the functionality of the entire gene. In order to differentiate between effects of subfunctionalization and dosage balance, we considered two different models, one where subfunctionalization is allowed and one where it is not.

FIG. 1.—

After a larger-scale duplication event, a fully duplicated network of three interacting partners including all links is obtained. Every gene is connected to each other gene through a link, except its own duplicate. These links are then allowed to decay in simulation with various constraints according to different evolutionary mechanisms. The fitnesses of the intermediate states are described in supplementary figure 1 (Supplementary Material online).

Under each model, each individual is assigned a fitness according to gene content and links present. The next generation is then sampled randomly with replacement, weighted by the fitness of each individual. A fitness penalty for each dosage imbalance is assigned and multiple fitness penalties in an individual are assessed multiplicatively. Individuals with a single fully linked network are assigned a fitness penalty of zero. In the case where subfunctionalization is allowed, a subfunctionalized network has no fitness penalty whereas in the other model, it has a fitness of zero. Imbalance states and corresponding fitness penalties are shown in supplementary figure 1 (Supplementary Material online). Fitness penalties for each imbalance ranged from 0.0 (control) to 0.4.

For each set of parameters (table 1), as well as different models, five replicates of the simulations were run. The total number of genes retained in duplicate copy was recorded for each generation, and the numbers of different replicas were averaged and plotted.

Table 1.

Simulations Generating the Retention Profiles in Figures 3–5 Were Generated with the Following Parameter Values Consistent with Different Mechanisms and Processes

Curve Name	Population Size	Network Size	Fitness Penalty	Pr(Link Loss)	Pr(Gene Loss)	SF Allowed	Pr(Neo Link)	Neo Fitness Adv.
3A	1,000	4	0.0	0.005	0.0001	No	0.0	0.0
3B	1,000	4	0.4	0.01	0.0001	No	0.0	0.0
3C	1,000	4	0.4	0.005	0.0001	No	0.0	0.0
3D	1,000	4	0.4	0.005	0.001	No	0.0	0.0
3E	1,000	4	0.4	0.00001	0.0001	No	0.0	0.0
3F	1,000	4	0.4	0.01	0.0001	Yes	0.0	0.0
3G	1,000	4	0.4	0.005	0.0001	Yes	0.0	0.0
3H	1,000	4	0.4	0.005	0.001	Yes	0.0	0.0
3I	1,000	4	0.0	0.005	0.0001	Yes	0.0	0.0
3J	1,000	4	0.4	0.00001	0.0001	Yes	0.0	0.0
3K	1,000	4	0.0	0.005	0.0001	No	0.0001	0.05
3L	1,000	4	0.0	0.005	0.0001	No	0.0001	0.2
3M	1,000	4	0.4	0.005	0.0001	No	0.0001	0.05
3N	1,000	4	0.4	0.005	0.0001	No	0.0001	0.2
4A	1,000	4	0.0	0.005	0.0001	No	0.0	0.0
4B	100	4	0.0	0.005	0.0001	No	0.0	0.0
4C	1,000	4	0.4	0.005	0.0001	No	0.0	0.0
4D	100	4	0.4	0.005	0.0001	No	0.0	0.0
5A	1,000	3	0.4	0.005	0.0001	No	0.0	0.0
5B	1,000	4	0.4	0.005	0.0001	No	0.0	0.0
5C	1,000	5	0.4	0.005	0.0001	No	0.0	0.0

NOTE.—Neo Fitness Adv., fitness advantage of a neofunctionalized individual; SF, subfunctionalization.

Simulations were implemented in Perl and the code is freely available at http://www.wyomingbioinformatics.org/LiberlesGroup/Anke_software.

General Death Model for Gene Retention

A model was constructed for which different sets of parameterization generate hazard curves indicative of different gene fates after a duplication event.

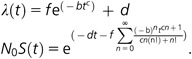λ(t) is the hazard function describing the instantaneous rate of loss. S(t) is the survival function describing the corresponding probability of survival to a time t, multiplied by N₀, the number of gene duplicates at t = 0. The f and d parameters allow for an instantaneous hazard rate at the point of duplication (d + f) to decay to an orthologous gene hazard rate (d), also creating a continuous function defined at t = 0. Hazard functions that correspond to the expected or theoretical shape of the hazard for the dosage balance (Hughes et al. 2007), subfunctionalization (Lynch et al. 2001; Hughes and Liberles 2007), neofunctionalization (Zhang et al. 2004; Hughes and Liberles 2007), and nonfunctionalization (Lynch and Conery 2003; Hughes and Liberles 2007) are given by contrasting parameter values (fig. 2). Nonfunctionalization is defined by b = 0, d > 10; dosage balance by b < 0, 0 < c < 1, d = −f, λ(t)_0.02 < 0.1; neofunctionalization by b > 0, 0 < c < 1, d > 0, f > 0; and subfunctionalization by b > 0, c > 1, d > 0, f > 0. Models have different numbers of parameters utilized and are compared by their likelihoods and Akaike information criterion (AIC) values. Parameterizations outside of these ranges were considered nonbiological and were not evaluated. Further evaluation on real data will be necessary to fully evaluate the biological parameterization ranges and misspecifications, but some support is given when comparing parameterizations on simulated data with those from O. dioica and from Hughes and Liberles (2007). To summarize the justification of the parameterizations, nonfunctionalization is reflected by a constant instantaneous rate of loss, neofunctionalization by a waiting time for a beneficial change, subfunctionalization by a double waiting time for complementary changes that result in a subfunctionalized state, and dosage balance by initial retention followed by subsequent cooperative loss with an increasing hazard.

Model Comparison on Simulated Data

Applying N₀S(t) evaluated with n = 100 on the simulated data enabled estimation of parameters representative of the different models, using a maximum likelihood estimator written in C++ using a probability library written by Brook Milligan (http://biology.nmsu.edu/software/probability). Maximum likelihood estimates were approximately with a least squares calculation according to Press et al. (1998). Parameter optimization utilized an uphill simplex method (Press et al. 1988) with multiple (100–400) simultaneous simplexes for each optimization. Generations were converted to dS using a factor of 10⁻⁴, an approximation to the mutation rate used in the simulation. The likelihood scores produced from subjecting the survival function to the estimated parameterization for each model of gene death are compared using AIC values. The best AIC along with the corresponding model and the parameterization of that model are given in table 2.

Table 2.

The General Loss Model Was Fit to the Data Shown in Figures 3–5, Generating Maximum Likelihood Parameterizations

Curve	Model	b	c	d	f
3A	Non			20.0
3B	Non			23.5
3C	D.B.	−25.2	0.231	−1.47e−06
3D	D.B.	−29.0	0.220	−3.17e−07
3E	D.B.	−13.8	0.105	−8.05e−09
3F	Sub	1,300	2.37	5.40e−04	5.84
3G	D.B.	−12.2	0.0450	−4.46e−05
3H	D.B.	−18.4	0.0484	−5.72e−07
3I	Sub	1,300	2.76	0.237	3.77
3J	D.B.	−14.4	0.0984	−5.03e−09
3K	Non			16.5
3L	Neo	42.2	0.0300	13.7	0.154
3M	D.B.	−13.5	0.0373	−2.80e−05
3N	D.B.	−14.4	0.0548	−2.55e−05
4A	Non			21.2
4B	Non			20.9
4C	D.B.	−23.9	0.215	−2.53e−06
4D	D.B.	−20.9	0.0622	−2.97e−08
5A	D.B.	−67.7	0.507	−3.67e−07
5B	D.B.	−24.6	0.240	−2.70e−06
5C	D.B.	−36.0	0.168	−3.52e−10

NOTE.—After adjusting for the number of parameters used in the various models with AIC, the maximum likelihood parameterization and the model it is consistent with are shown. D.B., dosage balance; Neo, neofunctionalization; Non, nonfunctionalization; Sub, subfunctionalization.

Model Comparison and Mixture Model Application to O. dioica Data

dS values of duplicated genes in the O. dioica genome were taken from published values (Denoeud et al. 2010), right truncated at dS = 0.3. Because the probability of multiple duplication events affecting a single gene increases, the pairwise estimate of the duplication rate becomes increasingly inaccurate beyond dS = 0.3. The Oikopleura data were previously fit by Denoeud et al. (2010) using a mixture model that did not enable mechanistic inference using a Bayesian framework. An initial approach used a maximum likelihood framework adapted from Hughes and Liberles (2007), similar to the approach popularized by Lynch and Conery (2000, 2003), where data were treated as bins of size 0.01 dS units, reducing the size of the data to 30 data points. The computation is as described for model comparison on simulated data. The mixture model application then evaluated multiple components of the survival function according to the formula illustrated below for two components:

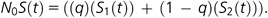Here, N₀ is the number of duplicates at t = 0 but is fit as a parameter model and q is the contribution of each mixture component. Birth was assumed to be constant in this model, where the birth rate is N₀/gene number. In future models, a more complex treatment of the birth process can be explored.

Results

Examination of Simulation Results

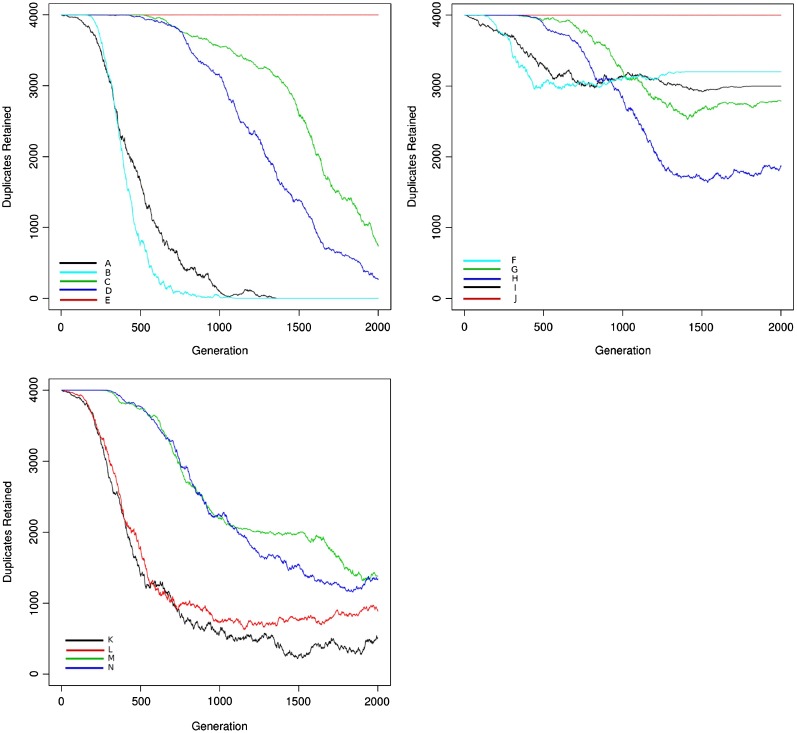
Simulation of duplicate gene retention showed that patterns of retention varied significantly depending upon model parameters (fig. 3). When subfunctionalization was allowed, it became the dominant fate, especially when link loss had a high probability relative to gene loss (fig. 3). Models that did not allow subfunctionalization decayed to loss of all duplicates, whereas models that did allow subfunctionalization did not. In models where dosage balance acted (with a high fitness penalty), a prolonged period of retention without loss was observed, both when subfunctionalization was allowed and when it was not. Neofunctionalization alone led to an increased retention of duplicates over the nonfunctionalization process, although in low frequency under the parameter settings used in curve 3K. In combination with dosage balance, neofunctionalization resulted in a similar pattern to the combination of subfunctionalization and dosage balance, although with expectedly different dynamics.

FIG. 3.—

Duplicate retention for the model including subfunctionalization (A), a model of dosage balance only (B), and a model combining neofunctionalization with dosage balance (C) in the case of four interacting partners and population size of 1,000 is shown. The neutral model (no dosage balance) is shown as black lines. Even under conditions of increased gene and/or link loss probabilities, dosage balance (pairwise link out-of-balance fitness penalty = 0.4) leads to the prolonged retention of gene duplicates in comparison with the neutral models. These curves were generated using the parameter values in table 1 for the network model and were fit with the parameter values from the loss model in table 2.

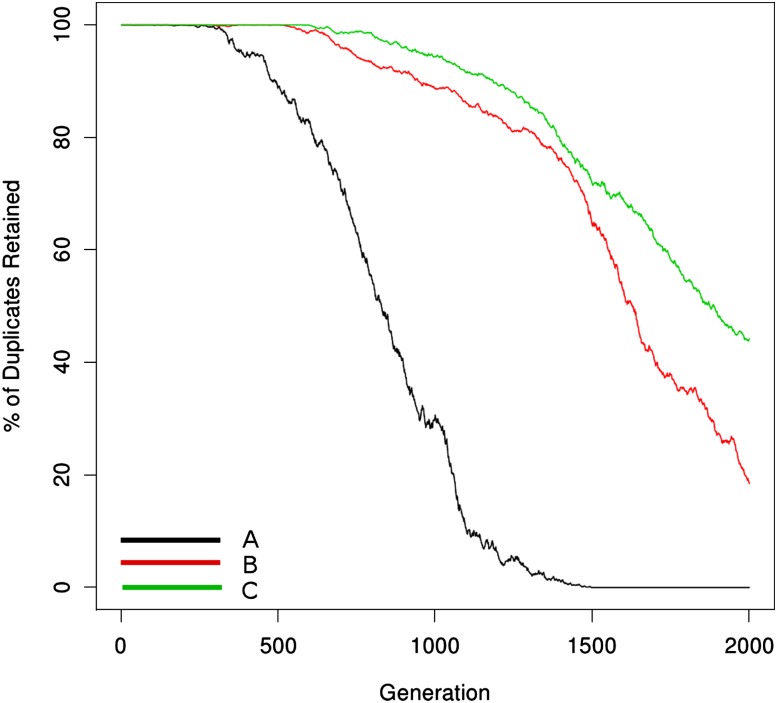
In figure 4, as expected by population genetic theory, smaller population sizes exhibit more stochasticity and a greater role for drift. In both population sizes in the simulation, dosage balance results in absolute initial preservation of the network across individuals. However, and consistent with predictions of Hughes et al. (2007), the greater efficiency of selection in the larger population size results in more rapid cooperative loss once individual genes are lost from the network. Further, in larger populations, segregating alleles may undergo additional mutations and fix multiple changes at once via stochastic tunneling (Iwasa et al. 2004), also consistent with the rapid complete loss observed in figure 4.

FIG. 4.—

The effect of population size on duplicate retention is shown. The black and green lines refer to the neutral model for population sizes 1,000 and 100, respectively. The red line shows dosage balance for a population size of 1,000, whereas the blue line shows that of population size 100. Whereas the duplicate retention under the neutral model behaves similarly between the two population sizes, dosage balance–driven loss is much more deterministic for the larger population size due to higher effectiveness of selection (Pr(lose gene) = 0.0001; Pr(lose link) = 0.005). The fitness penalty for links out-of-balance is 0.4. These curves were generated using the parameter values in table 1 for the network model and were fit with the parameter values from the loss model in table 2.

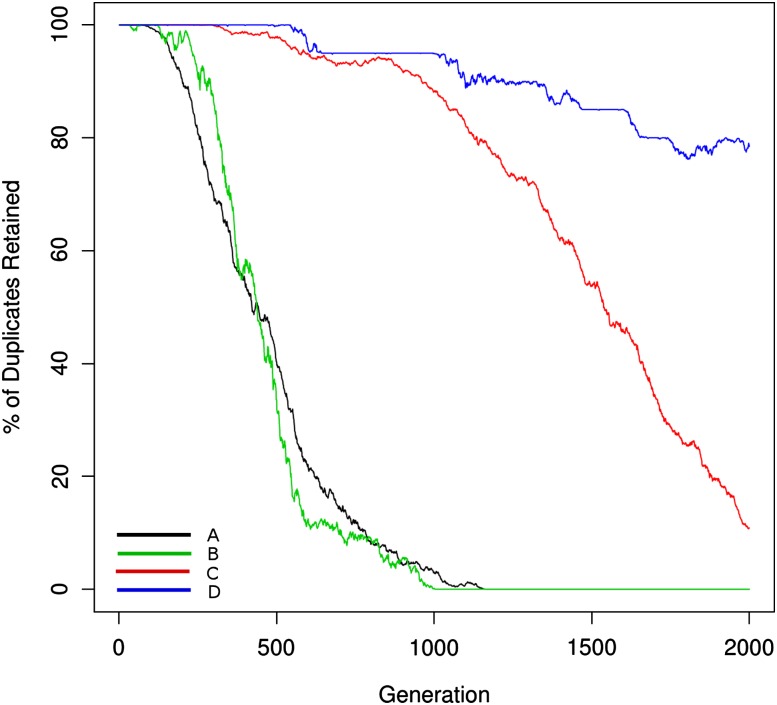
In figure 5, larger networks show stronger effects for increased dosage balance as evidenced by the prolonged retention periods of interacting networks. Hughes et al. (2007) predicted that cooperativity of loss would be dependent upon network size. The support for this hypothesis is not obvious from visual examination of the retention data but can be evaluated through model parameterization (below).

FIG. 5.—

Dosage balance for three different network sizes is shown. Larger network size corresponds to prolonged retention due to comparatively larger fitness effects of individual gene losses as well as the mutational opportunity to lose a gene from link loss being lower because there are more links to be lost before an entire gene is nonfunctionalized. The fitness penalty for links out-of-balance is 0.4. These curves were generated using the parameter values in table 1 for the network model and were fit with the parameter values from the loss model in table 2.

Model Comparison on Simulated Data

The General Death Model was applied to the simulated data described above. The model was based upon published theoretical expectations of dS-dependent retention of duplicates under different evolutionary mechanisms (Hughes and Liberles 2007; Hughes et al. 2007). Nonfunctionalization is a neutral process characterized by a constant instantaneous rate of duplicate gene loss (Lynch and Conery 2003; Hughes and Liberles 2007). Neofunctionalization involves a waiting time for a single advantageous change, resulting in a convexly declining hazard (Zhang et al. 2004; Hughes and Liberles 2007). Subfunctionalization involves a waiting time for two complementary deleterious changes, resulting in a concavely declining hazard (Lynch et al. 2001; Hughes and Liberles 2007). Dosage balance involves initial retention followed by cooperative loss once an initial gene duplicate is lost resulting in a concavely increasing hazard (Hughes et al. 2007). These expectations are independent of expectations of change in protein function or change in gene expression. Before evaluating simulated data from the network model, simulations generated from the distribution itself were tested. The model showed the ability to recapture parameterizations with small numbers of data points, although more data points were required to reject alternative null parameterizations with nonfunctionalization when AIC was utilized rather than simply likelihoods. This problem was somewhat alleviated with the restriction of the parameter range of nonfunctionalization to d > 10, which prevented a nonbiological slow loss process. This is justified by parameterizations on simulated and real data below as well as from the analysis in Hughes and Liberles (2007). The simulations are based upon a network model, where the action of various processes can occur simultaneously. The current version of the fit model will support parameterization of the mechanism that dominates the signal when multiple processes are acting.

As observed in table 2, the model comparison on the simulated data selects the proper mechanism in all cases. As is seen in curves 3G and 3H, these models reflect a combination of dosage balance and subfunctionalization. The mechanism that is selected depends upon the amount of data early in the simulation where dosage balance acts and provides signal compared with that late in the simulation where subfunctionalization acts and provides signal. With increasing time and corresponding data, these models will converge on a prediction of subfunctionalization. A comparison of curves 3A and 3B, although both are suggestive of nonfunctionalization according to the model, shows a neutral loss rate for 3A compared with selective pressure for loss in 3B, parameterized as a much steeper loss rate.

As with subfunctionalization, neofunctionalization also combines with dosage balance to yield a hybrid curve. In curve 3K, the parameterization of the simulation resulted in a small neofunctionalization effect. For this curve, the neofunctionalization model had the best likelihood, but due to the extra parameters, nonfunctionalization was preferred by AIC. Curve 3L, which had a stronger neofunctionalization effect, was properly identified as neofunctionalization. Curves 3M and 3N, like 3G and 3H, reflected hybrid processes and were identified with dosage balance as the dominant signal. Similarly, with increasing simulation time, the neofunctionalization signal will dominate over the dosage balance signal.

In figure 5, the parameterizations of the dosage balance model show much steeper increases in the rate of loss with increasing network size (as observed in the stepwise reduction of the c parameter toward 0). This parameterization provides some support for the hypothesis of cooperativity of loss that increases with the number of interacting partners as suggested in Hughes et al. (2007). However, a parameterization where the c value was held constant in 5A and 5C showed a lower likelihood, but this was not statistically significant when accounting for the reduction of one parameter in AIC. It may be that a model dominated by gene loss rather than link loss would show stronger statistical support for the cooperativity hypothesis.

Model Comparison and Mixture Model Application to O. dioica Data

The publication of the genome of the tunicate O. dioica included a characterization of recent duplicates based upon their pairwise dS values (Denoeud et al. 2010). These duplicates were originally fit with a mixture of a discrete distribution at dS = 0 and two Weibull components. The fit did not enable mechanistic inference but was suggestive of a Weibull fitting the loss process and a second Weibull fitting some variation in both the birth and loss process not described by the first component. There is no evidence of a recent whole-genome duplication in the Oikopleura genome, and the mechanistic modeling here is built upon the assumption of Lynch and Conery (2000, 2003) and of Hughes and Liberles (2007) of a constant birth rate that can be relaxed in future work. Unlike previous work, not only is the decay process more flexible, but the function is defined at t = 0 and can decay to asymptotic values >0.

A binning approach to fitting mixture models to duplicate data from the tunicate genome was performed, using maximum likelihood for parameter estimation (table 3). A one-component model showed support for a neofunctionalization parameterization (where most genes are nonfunctionalized, but those retained are retained through a process dominated by single-event waiting times) but with a c value close to 1 (0.948; a c value of 1 is equivalent to an exponential distribution, the neutral model). A two-component mixture showed two neofunctionalization components, one similar to the component in the one-component model with a c value at 0.725 and a weight of 58% and a second neofunctionalization-like component with steep decay and an initial high hazard (d >> f, d = 115), possibly fitting loss due to lack of fixation that was not explicitly modeled. However, the two-component mixture was not supported by AIC. The interplay between neofunctionalization parameterization and population genetic loss will be discussed further. A simple decay function as is commonly applied would be consistent with the nonfunctionalization mechanism parameterization but was not statistically supported by the data. The interpretation of these results, including caveats, will be discussed further.

Table 3.

Pairwise Duplicate Retention Data from the Oikopleura dioica Genome (Denoeud et al. 2010) Right Truncated at dS = 0.3 Was Fit with the General Death Model

Components	Model	AIC	N0	b	c	d	f	q
1	Neo	Yes	65.6	115	0.948	5.03	130
2	Neo	No	64.8	39.3	0.112	115	23.8	0.42
	Neo			46.2	0.725	4.45	74.0

NOTE.—AIC was used to compare parameterizations within a component class and between mixtures with different numbers of components. Using a fit to binned data, the best supported model was a one-component neofunctionalization model.

Discussion

Gene duplication is an important process in the functional divergence of genomes. To predict and understand how function diverges, mechanistic models to characterize duplicate gene retention and divergence are needed. The work described here has characterized duplicate retention processes when dosage balance acts as a mechanism, a process that has received less attention in the literature than subfunctionalization and neofunctionalization. Further, a general model for characterizing the retention of gene duplicates under different processes has been generated, extending the models of Lynch and Conery (2000, 2003) and of Hughes and Liberles (2007) to the dosage balance and subfunctionalization mechanisms. The work also generated support for the prediction of Hughes et al. (2007) that once a protein is lost from a network, there will be positive selective pressure to lose the additional copies under the dosage balance model and the strength of that selective pressure is dependent upon the number of interacting partners (cooperativity). The hypothesis that cooperativity increased with network size was supported in trend, but this was not statistically significant, and the lack of statistical support may be due to the nature of the simulated data (dominated by link loss rather than gene loss). Conversely, duplication of single genes in highly connected networks should be more strongly selected against. Indeed, such a trend is observable across the tree of life, and duplicability of proteins with high connectivity is greatly increased when a large-scale event (such as a whole-genome duplication) also duplicates their interacting partners (D'Antonio and Ciccarelli 2011).

The trends of gene duplicate loss and retention show an interesting interplay between mutation rate, fitness penalties, the size of the duplicated networks, and whether or not subfuntionalization occurs. We have shown that increased fitness penalties for pairwise links out of balance prolong the retention of duplicate genes in network settings. This strongly implies that not only are multiple interactions per gene in networks subject to subfunctionalization but that dosage balance can also play an intricate role in the retention of duplicates over long time periods. Whether the retention is due to subfunctionalization or dosage balance depends on the nature of the genes involved. As previously discussed, subfunctionalization is characterized by initial loss of duplicates, followed by high retention once subfunctionalization is achieved, whereas dosage balance causes initial retention, followed by cooperative loss. If the genes in the interaction network function in such a way that interactions cannot be separated temporally or spatially (as implied in our dosage balance–only model), then the trends seen strictly follow the dosage balance expectations. However, when the interactions can be separated, subfunctionalization produces the dominant signal seen. This is a result consistent with graph theory expectations that link the probability of gaining or losing links to the probability of retaining complete networks, known as the Erdös–Rényi Model (Bollobás and Erdős 1976) for the case of a completely random network (of which this is a generalization).

In the context of protein interaction networks and the nature of the binding interface, it is possible to predict when subfunctionalization might be possible. As noted above, when highly connected proteins participate in a complex (coexpressed, often referred to as “party hubs”; Ekman et al. 2006), the cause of the fitness loss due to dosage imbalance, including over-/underwrapping leading to incorrect complex assembly (Liang et al. 2008), makes it highly improbable that interactions could be partitioned in a way that maintains fitness. Additionally, there is a large expected difference in pleiotropic constraint between proteins that bind different partners via multiple interfaces and those that concentrate multiple interactions to a single binding patch (Kim et al. 2006). Although interaction network data with this type of structural resolution are currently rather sparse, the rapid growth of the number of experimentally determined protein complexes (Juettemann and Gerloff 2011) should aid this type of model inference in the near future. An additional layer of biological complexity that will not appear in databases but that will be subject to this type of selective constraint with dosage effects and subfunctionalization are selective pressures on what not to bind (Liberles et al. 2011). Although this will not affect application of the general model for loss, it will affect data interpretation.

The general model described was based upon expected hazard functions under different evolutionary mechanisms as shown in figure 2. The expectations derive from the mathematics associated with the processes being described. However, there are additional considerations worth discussing. Because the rates of deleterious and advantageous mutation are different, this may affect the parameterization of the subfunctionalization and neofunctionalization models in a manner that was not considered. This will need future calibration on real data. Although the expectations of the model associated with the mechanism are correct, parameterization of rapid neofunctionalization might suggest that neofunctionalization has a faster decay in the hazard than subfunctionalization, whereas simulation (Rastogi and Liberles 2005) and genetic data analysis (He and Zhang 2005) have suggested that subfunctionalization occurs more rapidly than neofunctionalization.

Further, the model treats nonfunctionalization as the dominant process leading to loss and does not describe the population genetic process that can lead to loss with very different dynamics. It is possible that rapid loss under this model contributes to support for the neofunctionalization-type parameterizations. However, in the Oikopleura data where neofunctionalization was supported, a second model with a second neofunctionalization-like component involving rapid decay was not statistically supported. Additionally, the simulated data did not give false support for neofunctionalization even though the population genetic process of loss occurred in the simulation.

Biologically, the analysis of the O. dioica duplicates here, like that of mammalian duplicates (Hughes and Liberles 2007), was consistent with a neofunctionalization model. Although there are caveats (listed above) to this biological data interpretation, one interpretation might be that neofunctionalization is indeed an important process for the retention of duplicated genes, even in small population size organisms. Examination of selection through dN/dS ratios (the ratio of nonsynonymous to synonymous nucleotide substitution rates) in Oikopleura did show evidence for a large N_eu (the effective population size multiplied by the mutation rate), making suggestions of neofunctionalization less surprising than for mammals (Denoeud et al. 2010). Further, understanding any departure from simple neutral population genetic expectations (Lynch et al. 2001) might have roots in biophysics, where adaptive changes of binding functions in proteins and of transcription factor–DNA interactions regulating transcription are actually much more common, with more mutational opportunity than is commonly thought in the population genetics literature. Indeed, it may be that gain of a gene expression domain (e.g., time in development or tissue where a gene is expressed) shows a greater mutational opportunity than complementary loss of expression domains, and this has indeed been observed among duplicates retained after the teleost whole-genome duplication event (e.g., Østbye et al. 2001).

Further, it has recently been suggested that interactome complexity can be built up in small population size organisms through neutral processes, resulting in secondary selection for protein–protein interactions to maintain proper function (Fernández and Lynch 2011). This mechanism would also interplay with expanded mutational opportunities for new protein–protein interactions in small population size organisms. Further consideration of the underlying physical chemistry of protein–protein interaction in an evolutionary context will illuminate these possibilities.

The model fitting that supported a single neofunctionalization model on the Oikopleura data was based upon a fit to 30 bins of data, as has been applied in the comparative genomics literature. Because bin size introduces an arbitrary component to the model, an alternative approach that can be conceived is to use the right truncated probability density function to fit the continuous data. This approach may have more power to support a mixture model with additional components that may be biologically informative and will be described elsewhere.

Another current debate in the molecular evolution literature is on the relative importance of change at the gene expression and at the protein-coding levels. The model does not currently enable differential prediction of changes at the protein-coding level and those at the gene expression level. For both neofunctionalization and subfunctionalization, there are different expectations for the evolution of dN/dS ratios relative to dS ratios when the protein function is changing as opposed to when change is occurring at the level of gene expression. A future version of this model can include dN/dS versus dS evolution as part of the likelihood. A framework for evaluating this was presented in Hughes and Liberles (2007). When genes are changing function at the gene expression level, negative selection is expected on the coding sequence. Neofunctionalization of protein function is expected to show positive selection detectable with dN/dS. Dosage-balanced genes will be expected to show negative selection until they are being lost. Simulations will be necessary to characterize these expectations more fully.

The model described deals exclusively with gene loss and retention from a birth event. Variation in the birth rate in small-scale duplication events may be an important consideration for modeling duplicates, and attention will also have to be paid to modeling of the birth process, potentially as a mixture model involving different constant rate processes or involving the addition of discrete distributions when statistically supported. Variation in the birth process and extending this framework to the analysis of a mixture of small-scale duplication and whole-genome duplication will become a critical next step.

The models that have been described have been applied to the pairwise analysis of duplicates in the O. dioica genome. It is well known that phylogenetic analysis outperforms pairwise analysis on comparative genomic data. The models described can be extended to the gene tree/species tree reconciliation problem, and this will also be an important future trajectory. Powerful tools for mechanistic functional characterization of gene duplicates will be increasingly valuable as computational comparative genomics moves forward.

Supplementary Material

Supplementary figure 1 is available at Genome Biology and Evolution online (http://www.gbe.oxfordjournals.org/).