Experimental Evidence for Water Mediated Electron-Transfer Through Bis-Amino Acid Donor-Bridge-Acceptor Oligomers

Abstract

This work compares the photoinduced unimolecular electron transfer rate constants for two different solute molecules (D-SSS-A and D-SRR-A) in water and DMSO solvents. The D-SSS-A solute has a cleft between the electron donor and electron acceptor unit, which is able to contain a water molecule but is too small for DMSO. The rate constant for D-SSS-A in water is significantly higher than that for D-SRR-A, which lacks a cleft, and significantly higher for either solute in DMSO. The enhancement of the rate constant is explained by an electron tunneling pathway that involves water molecule(s).

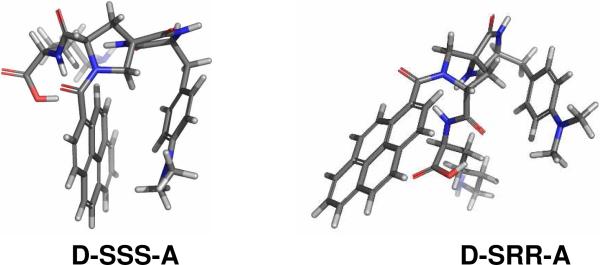
Water molecules influence electron transport in biomolecules and play a key role in biologically vital processes in living cells.^1-3 The importance of water in determining the activation energy for electron transfer (ET) reactions is well appreciated. Recent theoretical work shows that placement of a few water molecules between electron donor and acceptor moieties can change the electronic tunneling probability between them.^4-6 Although some experimental studies have probed electron tunneling in frozen water^7,8 the experimental study of electron tunneling through water molecules under ambient conditions is lacking. This work investigates the role of water molecules by studying the photoinduced electron transfer rate in two Donor-Bridge-Acceptor (DBA) bis-amino acid oligomers that contain a pyrene carboxamide group as an acceptor unit and dimethylaniline (DMA) as a donor unit in water and DMSO. The DBA molecules differ by their bridge stereochemistry (Figure 1). One amide rotamer of the D-SSS-A bridge forms a cleft between the donor and acceptor whereas the D-SRR-A bridge geometry does not form any well defined cleft. Here SSS and SRR indicate the stereochemistry at the α-carbon of the dimethylaminophenylalanine residue and the 2 and 4 positions of the pyrrolidine ring respectively. This difference in geometry also provides two different “line-of-sight” donor to acceptor distances 4.6 Å and 9.7 Å, respectively, but the same number and types of covalent bonds through the bridge.⁹

Figure 1.

Structures of bis-amino acid DBA molecules with different bridge stereochemistry are shown.

Work in organic solvents shows that photoinduced electron transfer in DBA supermolecules with a cleft between the donor and acceptor moieties can proceed by electron tunneling through solvent molecules residing in the cleft.^10-13 The ET rates of the two compounds in Figure 1 were studied in two different solvents, water and dimethyl sulphoxide (DMSO), as a function of temperature to probe the effect of water molecules on the ET kinetics and compare to DMSO as a ‘control’ solvent. Synthesis of the bis-amino acid oligomers with different length has been reported elsewhere¹⁴ (see Supporting Information).

One-dimensional ¹H NMR experiments indicate that D-SSS-A in both D₂O and DMSO and D-SRR-A in D₂O at 330 - 333 K each occupy two rotameric conformations with essentially identical average population ratios (see Table 1). In both solvents, the more populated conformation of D-SSS-A is the cleft conformation shown in Fig. 1, in which the pyrene is rotated close to the dimethylaniline hydrogens resulting in upfield chemical shifts of the DMA peaks. These data indicate that the conformational preferences of the DBA molecules are similar in DMSO and H₂O.

Table 1.

Electron transfer parameters (|V|, Δ_rG, λ_S) and rotamer populations for D-SSS-A and D-SRR-A

DBA/solvent	|V|(cm-1)b	ΔrG (eV)b	λS (eV)26	Pop.a
D-SSS-A/H2O	35 ± 6	-0.66 ± 0.02	1.42	63:37
D-SRR-A/H2O	12 ± 2	-0.54 ± 0.01	1.12	63:37
D-SSS-A/DMSO	11 ± 2	-0.55 ± 0.01	1.12	65:35
D-SRR-A/DMSO	13 ± 2	-0.36 ± 0.01	0.91	n/d

^aPopulation ratio of two amide rotamers at 330 – 333K

^bError shows effect of a ±0.1 eV variation in λ_S

The molecules in Figure 1 have the same donor and acceptor unit, and ET occurs when the pyrene carboxamide moiety is electronically excited by 330 nm light. This donor and acceptor pair has been used for intramolecular ET studies in different organic solvents in the past.^15, The fluorescence decay law is well described by a double exponential and the two time components are ascribed to the two rotamers; the longer decay time is the less populated conformer (donor and acceptor far apart) and the short decay time is the more populated conformer; those shown in Fig. 1. The short lifetime component was used to determine the electron transfer rate constant, k_ET, for the cleft rotamer (details in Supplemental Information).¹⁶ The pH of the water solution was kept ~7 to avoid any protonation of the amine group of the dimethylaniline donor unit.¹⁷

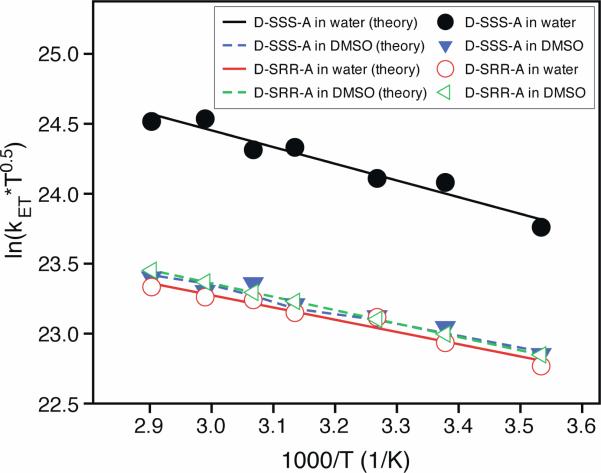
Figure 2 shows how k_ET for D-SRR-A and D-SSS-A depend on temperature, in water and DMSO. The activation energies are very similar (ranging from 1.5 kJ/mol to 2.1 kJ/mol). For D-SSS-A k_ET is about three times larger in water than in DMSO and is three times larger than the k_ET measured for D-SRR-A.

Figure 2.

These plots show the temperature dependence of the k_ET for D-SSS-A in water (filled circle) and DMSO (filled triangle) and for D-SRR-A in water (open circle) and DMSO (open triangle). The lines represent fits by the semiclassical ET model.

The semiclassical electron transfer theory expresses the electron transfer rate constant as the product of the square of the electronic coupling, |V|², and the Franck-Condon weighted density of states (FCWDS). Using the semiclassical Marcus equation^18,19 to calculate the rate constant requires knowledge of the electronic coupling (|V|), the Gibbs free energy (Δ_rG), the solvent reorganization energy (λ_S), and the internal reorganization energy parameters.^20,21 The internal reorganization energy parameters (λ_V and ν) are primarily determined by the molecular characteristics of the donor and acceptor, and the values for pyrene and dimethylaniline were taken from a previous study¹⁵ to be λ_V = 0.19 eV and ν = 1400 cm^-1. The lines in Fig 2 show fits of the experimental rate data by this model with Δ_rG and |V| as adjustable parameters. The solvent reorganization energy λ_S was calculated using a continuum model.^22,23 The values for the reorganization energies were kept constant throughout the analysis; i.e., no temperature dependence was included.

The Δ_rG and |V| obtained from the fit are reported in Table 1. The Δ_rG is found to be more negative for compound D-SSS-A than D-SRR-A in water and DMSO. The difference in Gibbs energy for D-SSS-A and D-SRR-A likely reflects the difference in Coulomb stabilization of the charge separated state, however an accurate assessment will require modeling that includes the electrostatic properties and polarizability of the solvent molecules, as well as the solute.^24,25 The |V| obtained from the fits are very similar for the two solutes in DMSO, however the |V| obtained for D-SSS-A in water is significantly higher than that found for D-SRR-A in water. In all cases the coupling values are modest and consistent with a nonadiabatic coupling mechanism.

The enhancement in |V| for D-SSS-A in water, over that for D-SRR-A, may reflect a change in the tunneling pathway, from a bridge mediated process to a solvent mediated process. The similarity of the electronic coupling for D-SRR-A in DMSO and H₂O suggests that the coupling is determined by a bridge mediated superexchange interaction, hence it is solvent independent. In contrast, the cleft molecule D-SSS-A shows a solvent dependence (a larger |V| for H₂O than for DMSO). For a donor to acceptor distance of 4.5 Å and accounting for the π-cloud extents, the space available in the cleft is about 1.2 Å.²⁷ This value is comparable to the van der Waals radius of H₂O (ca. 1.4 Å) but significantly smaller than that of a DMSO molecule (ca. 2.5 Å).²⁸ Hence we postulate that for DMSO the electron tunneling must occur through the ‘empty’ cleft or by way of the bridge, whereas in water an H₂O molecule can reside in the cleft and mediate the electron tunneling or bind alongside the cleft to act as a short bridge/tunneling pathway.

An alternative mechanism to explain the observations involves proton motion that is coupled to the ET,^29-31 i.e., a proton coupled electron transfer (PCET). To evaluate this possibility, k_ET was determined for the DBA compounds in deuterium oxide (D₂O). A significant normal kinetic isotope effect was observed (k_ET,H2O/k_{ET, D2O} = 1.49 for D-SSS-A and k_ET, _H2O/k_{ET, D2O} = 1.17 for D-SRR-A at 295K). Both molecules display an isotope effect, however it is more pronounced in D-SSS-A. The detailed origin of the enhancement of the rate for D-SSS-A in water requires further investigation.

Whichever mechanism operates, it seems clear that electron transfer for D-SSS-A involves one or more H₂O molecules. The higher k_ET for D-SSS-A/H₂O, as compared to the similar rates for D-SRR-A/ H₂O and both solutes in DMSO, suggests that water molecules play a special role for D-SSS-A/H₂O. The observation of an isotope effect that is stronger for D-SSS-A than for the D-SRR-A system suggests that hydrogen bonded network(s) protons play a role. In terms of the semiclassical model, the higher k_ET for D-SSS-A/H₂O as compared to DMSO can be attributed to a higher |V|. An analysis using this model and a dielectric continuum description for the solvent reorganization energy indicates that the electronic coupling values for D-SRR-A and for either solute in DMSO are very similar (see Table 1), whereas that for D-SSS-A in water is three times larger. It is important to note that many solvent/solute conformations are possible and thermally sampled, so that the |V| in Table 1 should be considered a root mean square value (see reference 10). These experimental results in water substantiate earlier theoretical predictions that water molecules located in the vicinity of donor and acceptor units can mediate the electronic coupling; i.e., electron transfer can proceed by tunneling through water molecule(s).