The Population Genetics of X–Autosome Synthetic Lethals and Steriles

Abstract

Epistatic interactions are widespread, and many of these interactions involve combinations of alleles at different loci that are deleterious when present in the same individual. The average genetic environment of sex-linked genes differs from that of autosomal genes, suggesting that the population genetics of interacting X-linked and autosomal alleles may be complex. Using both analytical theory and computer simulations, we analyzed the evolutionary trajectories and mutation–selection balance conditions for X–autosome synthetic lethals and steriles. Allele frequencies follow a set of fundamental trajectories, and incompatible alleles are able to segregate at much higher frequencies than single-locus expectations. Equilibria exist, and they can involve fixation of either autosomal or X-linked alleles. The exact equilibrium depends on whether synthetic alleles are dominant or recessive and whether fitness effects are seen in males, females, or both sexes. When single-locus fitness effects and synthetic incompatibilities are both present, population dynamics depend on the dominance of alleles and historical contingency (i.e., whether X-linked or autosomal mutations occur first). Recessive synthetic lethality can result in high-frequency X-linked alleles, and dominant synthetic lethality can result in high-frequency autosomal alleles. Many X–autosome incompatibilities in natural populations may be cryptic, appearing to be single-locus effects because one locus is fixed. We also discuss the implications of these findings with respect to standing genetic variation and the origins of Haldane’s rule.

NONADDITIVE (epistatic) genetic interactions are ubiquitous in biological organisms (Wolf et al. 2000; Moore 2003; Mackay 2004; Phillips 2008). The nature and intensity of such epistasis have important implications for the evolution of sex (Otto and Lenormand 2002; de Visser and Elena 2007), the evolution of hybrid incompatibility (speciation) (Dobzhansky 1937; Muller 1942; Orr 1995; Johnson 2000a,b; Coyne and Orr 2004; Gavrilets 2004), and other aspects of evolutionary biology. Epistasis can also lead to different QTL being identified in different populations (Liao et al. 2001; Wade 2001). It can also explain some of the “missing heritability” of genome-wide association studies in human genetics (Manolio et al. 2009; Moore et al. 2010). Evolutionary geneticists have long debated the importance of interactions vs. single-locus fitness effects (Crow 1987; Willis and Orr 1993; Yukilevich et al. 2008).

An important subset of epistatic interactions involves deleterious phenotypes that occur only in the presence of a combination of two or more alleles at different loci. Theodosius Dobzhansky first described synthetic lethals as interacting chromosomes whose effects were released through recombination (Dobzhansky 1946). A modern definition of synthetic lethality is “any combination of two separately nonlethal mutations that leads to inviability” (Ooi et al. 2006, p. 57). More broadly, synthetic incompatibilities can involve either synthetic lethality or synthetic sterility. As synthetic incompatibilities need not lead to complete lethality or sterility, Phillips and Johnson (1998) used the term “synthetic deleterious loci”.

Synthetic incompatibilities are important because they influence allele frequency trajectories and patterns of standing genetic variation. Because genotypes at one locus can mask the effects of genotypes at another locus, synthetic incompatibilities are able to segregate at higher frequencies than nonepistatic deleterious alleles. For example, at mutation–selection balance, the expected frequencies of double recessives are on the order of $\sqrt[4 ]{\mu /s}$, where μ and s are mutation rates and selection coefficients (Phillips and Johnson 1998). In contrast, single-locus expectations are on the order of $\sqrt[2 ]{\mu /s}$ (Charlesworth and Charlesworth 2010). If mutation rates differ between loci involved in synthetic lethality, mutation pressure can slowly cause alleles at either locus to fix. Interestingly, genetic systems during this convergence process may appear to have single-locus mutation–selection balance with incomplete penetrance (Christiansen and Frydenberg 1977). Dominance complicates the population genetics of autosomal synthetic lethals, as does linkage (Bengtsson and Christiansen 1983; Phillips and Johnson 1998).

Important differences exist between X-linked and autosomal variation: males are hemizygous for most X-linked genes and X chromosomes spend two-thirds of their time in females. Asymmetry between X-linked and autosomal genes can influence evolutionary trajectories (Charlesworth et al. 1987). Moreover, genomic data reveal that DNA sequences evolve at different rates on the X chromosomes and the autosomes (Vicoso and Charlesworth 2006; Singh et al. 2008; Gottipati et al. 2011). Are incompatible alleles more likely to segregate at higher frequencies at X-linked loci or at autosomal loci? Because existing theory has focused on autosomal synthetic incompatibilities, there is a clear need to examine X–autosome interactions.

Ample evidence of synthetic incompatibilities exists in natural and experimental populations. Many early examples of synthetic lethality were found in a variety of Drosophila species (Dobzhansky 1946; Lucchesi 1968; Temin et al. 1969; Thompson 1986). More recently, synthetic lethality and sterility were found between naturally segregating X chromosomes and autosomes in Drosophila melanogaster (Lachance and True 2010). This study found higher levels of incompatibility between chromosomes derived from different geographical locations, suggesting that population structure can favor the accumulation of X–autosome incompatibilities. Synthetic incompatibilities have been used to map genetic networks in Caenorhabditis elegans and Saccharomyces cerevisiae (Tong et al. 2004; Lehner et al. 2006; Ooi et al. 2006). Evidence from these studies suggests that <4% of all pairwise combinations are synthetic lethal or sublethal and most genes are synthetic lethal with <10 other genes (Hartman et al. 2001; Davierwala et al. 2005). Experiments using RNA viruses also indicate that many synthetic interactions are deleterious (Sanjuan et al. 2004).

X–autosome incompatibilities also may explain a long-standing empirical generalization known as Haldane’s rule (Coyne and Orr 2004; Schilthuizen et al. 2011). This pattern, first noted by J. B. S. Haldane (Haldane 1922), states that if only one sex of a hybrid has reduced fitness, it tends to be the heterogametic sex. Although the causes of Haldane’s rule are multifarious and complex (Orr 1993a; Wu and Davis 1993; Laurie 1997; Coyne and Orr 2004), there is consensus that X-linked genes play a predominant role in hybrid incompatibility (Tao et al. 2003; Masly and Presgraves 2007; Presgraves 2008). It seems likely that Haldane’s rule is at least in part due to interactions between these X-linked genes and autosomal genes.

This study contains a theoretical treatment of the dynamics of X–autosome synthetic incompatibilities. First, we develop a general model that includes sex-specific allele frequencies and fitnesses. Focusing on epistatic interactions in the absence of single-locus fitness effects, we consider synthetic lethality (in which both sexes have reduced fitness) and synthetic sterility (in which only a single sex has reduced fitness). In each of these scenarios we explore allele frequency trajectories and mutation–selection balance at both loci. We then relax the assumption that single-locus fitness terms are absent and examine what happens when synthetic incompatibilities are opposed by alleles that are beneficial when found singly. Testable predictions arise; for instance, we can predict which incompatible allele (autosomal or X-linked) is more likely to segregate at a higher frequency.

General Model

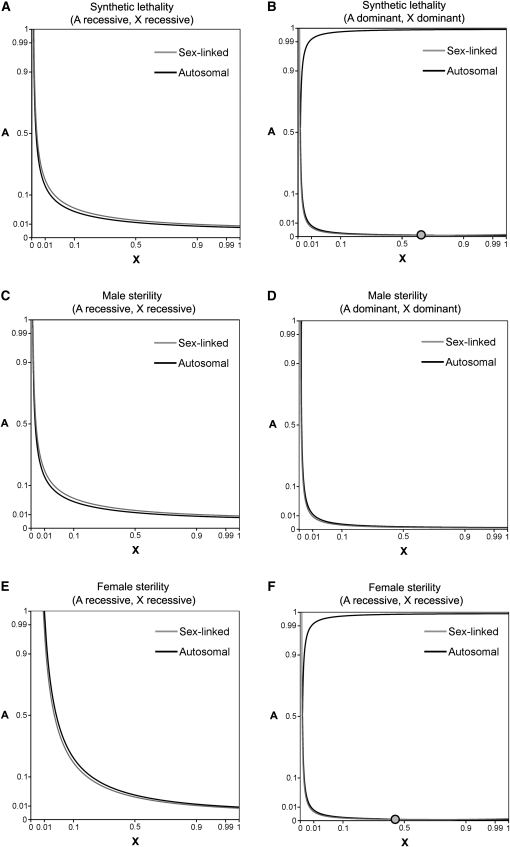
We consider a two-locus population genetics model with discrete generations, infinite population size, and equal sex ratios prior to selection. One locus is autosomal (segregating alleles A and a), and the other locus is X-linked (segregating alleles X and x). Synthetic incompatibilities exist between A and X alleles. We allow these incompatibilities to be sex specific and involve various types of dominance. Each generation, natural selection occurs subsequent to forward mutation (mutations rates from a to A are given by μ_A, and mutations from x to X are given by μ_X). For mathematical simplicity, we ignore back mutation. Realistic mutation rates in humans range from $1.1\hspace{0.17em}\times \hspace{0.17em}{10}^{-8}$ to $2.5\hspace{0.17em}\times \hspace{0.17em}{10}^{-8}$ mutations per nucleotide per generation (Nachman and Crowell 2000; Roach et al. 2010) or ∼$1\hspace{0.17em}\times \hspace{0.17em}{10}^{-5}$ mutations per gene per generation. Realistic selection coefficients range from complete lethality ($s=1$) to nearly neutral fitness effects ($N_{\text{e}}s<1$), and empirical data indicate that the distribution of fitness effects is bimodal (Eyre-Walker and Keightley 2007). To better depict allele frequencies that are close to zero or one, many figures in this article use an arcsine square-root scale (Figures 1, 2, 3, 5, and 7).

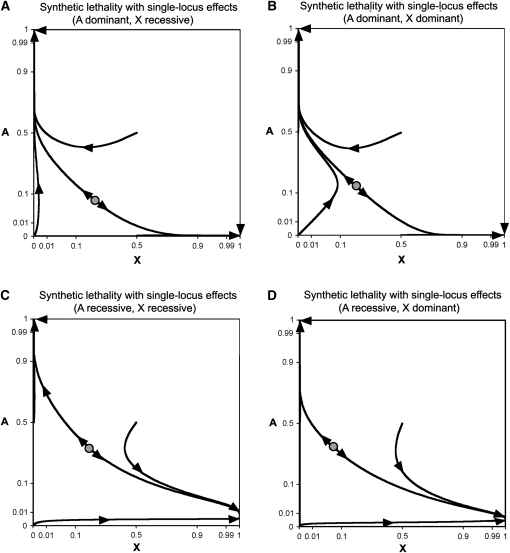
Figure 1 .

Autosomal and X-linked mutation–selection balance. Allele frequency combinations in which mutation–selection balance occurs for one locus need not entail mutation–selection balance at the other locus. Single-locus fitness effects are assumed to be absent. Autosomal mutation–selection balance curves are solid, and X-linked mutation–selection balance curves are shaded. Each panel corresponds to different types of fitness dominance and selection: (A) synthetic lethality with complete recessivity at both loci, (B) synthetic lethality with complete dominance, (C) synthetic male sterility with complete recessivity, (D) synthetic male sterility with complete dominance, (E) synthetic female sterility with complete recessivity, and (F) synthetic male sterility with complete dominance. Selection coefficients are $s_{\text{I,male}}=1$, $s_{\text{I,fem}}=1$ for synthetic lethality, $s_{\text{I,male}}=1$, $s_{\text{I,fem}}=0$ for synthetic male sterility, and $s_{\text{I,male}}=0$, $s_{\text{I,fem}}=1$ for synthetic female sterility. Mutation rates equal ${10}^{-5}$. Unstable internal equilibria are denoted with shaded circles, and axes use an arcsine square-root scale.

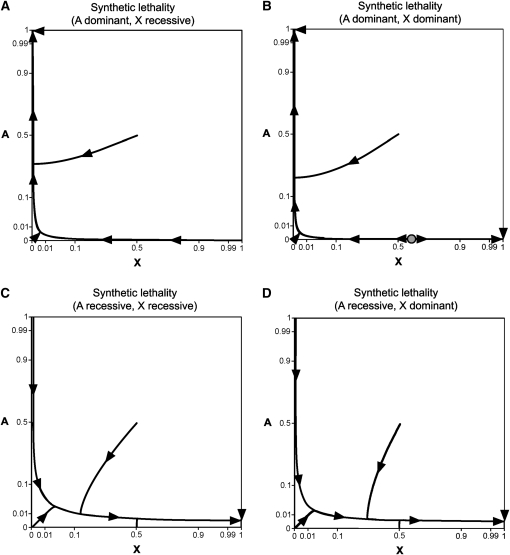
Figure 2 .

Allele frequency trajectories for synthetic lethality. Fitnesses are the same for males and females ($s_{\text{I,male}}=1$, $s_{\text{I,fem}}=1$, $s_{\text{A,male}}=0$, $s_{\text{A,fem}}=0$, $s_{\text{X,male}}=0$, $s_{\text{X,fem}}=0$). Each panel depicts a different type of fitness dominance: (A) complete autosomal dominance and X-linked recessivity, (B) complete dominance at both loci, (C) complete recessivity at both loci, and (D) complete autosomal recessivity and X-linked dominance. Mutation rates equal ${10}^{-5}$. Curves were generated by iterating the equations for allele frequency change. Directions of allele frequency change are denoted with solid arrowheads. In B, a shaded circle denotes an unstable internal equilibrium. Axes use an arcsine square-root scale.

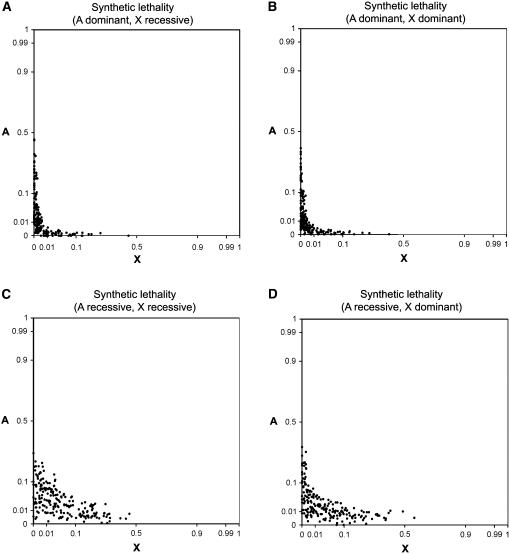
Figure 3 .

Synthetic lethality simulations. Data were generated via Monte Carlo simulations in MATLAB. Data points indicate allele frequencies after 5000 generations of evolution, and simulations were run 200 times for each type of fitness dominance: (A) complete autosomal dominance and X-linked recessivity, (B) complete dominance at both loci, (C) complete recessivity at both loci, and (D) complete autosomal recessivity and X-linked dominance. Parameter values are $\mu ={10}^{-5}$, $s_{\text{I,male}}=1$, $s_{\text{I,fem}}=1$, $s_{\text{A,male}}=0$, $s_{\text{A,fem}}=0$, $s_{\text{X,male}}=0$, $s_{\text{X,fem}}=0$, and population size = 10,000 individuals. Axes use an arcsine square-root scale.

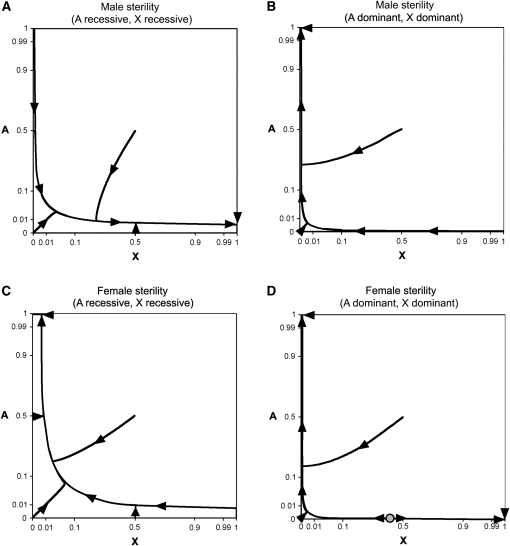
Figure 5 .

Allele frequency trajectories for synthetic sterility. Selection coefficients for male sterility are $s_{\text{I,male}}=1$ and $s_{\text{I,fem}}=0$. Selection coefficients for female sterility are $s_{\text{I,male}}=0$ and $s_{\text{I,fem}}=1$. Single-locus fitness effects are assumed to be absent. Mutation rates equal ${10}^{-5}$. (A) Synthetic male sterility with complete recessivity; (B) synthetic male sterility with complete dominance; (C) synthetic female sterility with complete recessivity; (D) synthetic female sterility with complete dominance. Curves were generated by iterating the equations for allele frequency change. Directions of allele frequency change are denoted with solid arrowheads, and a shaded circle denotes an unstable internal equilibrium in D. Axes use an arcsine square-root scale.

Figure 7 .

Allele frequency trajectories of synthetic incompatibilities with single-locus fitness effects. Fitnesses are the same for both sexes. Single-locus and epistatic fitness effects are in opposite directions ($s_{\text{I,male}}=1$, $s_{\text{I,fem}}=1$, $s_{\text{A,male}}=-0.1$, $s_{\text{A,fem}}=-0.1$, $s_{\text{X,male}}=-0.1$, $s_{\text{X,fem}}=-0.1$), and mutation rates equal ${10}^{-5}$. Each panel depicts a different type of fitness dominance: (A) complete autosomal dominance and X-linked recessivity, (B) complete dominance at both loci, (C) complete recessivity at both loci, and (D) complete autosomal recessivity and X-linked dominance. Curves were generated by iterating the equations for allele frequency change. Directions of allele frequency change are denoted with solid arrowheads, and shaded circles denote unstable internal equilibria. Axes use an arcsine square-root scale.

Because X-linked and autosomal alleles are on different chromosomes, our study tracks allele frequencies rather than haplotype frequencies. Allele frequencies in males are given by A_male and X_male, and allele frequencies in females are given by A_fem and X_fem (Table 1). These are postselection allele frequencies.

Table 1 . List of parameters for the X–autosome model.

Parameter	Meaning
Amale	Frequency of A allele in males
Afem	Frequency of A allele in females
Xmale	Frequency of X allele in males
Xfem	Frequency of X allele in females
sA,male	Selection coefficient in males due to autosomal alleles
sA,fem	Selection coefficient in females due to autosomal alleles
sX,male	Selection coefficient in males due to X-linked alleles
sX,fem	Selection coefficient in females due to X-linked alleles
sI,male	Selection coefficient in males due to epistatic interactions
sI,fem	Selection coefficient in females due to epistatic interactions
hA	Autosomal dominance coefficient
hX	Sex-linked dominance coefficient
${\overline{w}}_{\text{male}}$	Mean fitness of males
${\overline{w}}_{\text{fem}}$	Mean fitness of females
wA,male	Marginal fitness of A alleles in males
wA,fem	Marginal fitness of A alleles in females
wX,male	Marginal fitness of X alleles in males
wX,fem	Marginal fitness of X alleles in females
μA	Mutation rate at the autosomal locus
μX	Mutation rate at the X-linked locus

Selection coefficients are allowed to differ in males and females, and subscripts indicate selection coefficients that are due to autosomal fitness effects (s_A,male and s_A,fem), X-linked fitness effects (s_X,male and s_X,fem), and epistatic interactions (s_I,male and s_I,fem). For consistency with previous studies, positive selection coefficients refer to deleterious fitness effects (Table 2). Male sterility refers to scenarios in which selection coefficients are zero in females and nonzero in males, and female sterility refers to scenarios in which selection coefficients are zero in males and nonzero in females. Technically, male sterility and female sterility scenarios also apply to situations where there is sex-specific lethality. Because our study focuses primarily on X–autosome epistasis, many subsections in this study assume that single-locus fitness effects are absent ($s_{\text{A,male}}=0$, $s_{\text{A,fem}}=0$, $s_{\text{X,male}}=0$, $s_{\text{X,fem}}=0$). We subsequently relax this assumption to examine what happens when single-locus fitness effects and synthetic incompatibilities are both present.

Table 2 . Fitness matrix.

		Autosomal genotype
		AA	Aa	aa
Sex chromosome genotype	XY	1 – sA,male – sX,male – sI,male	1 – sA,malehA – sX,male –sI,malehA	1 – sX,male
	xY	1 – sA,male	1 – sA,malehA	1
	XX	1 – sA,fem – sX,fem – sI,fem	1 – sA,femhA – sX,fem –sI,femhA	1 – sX,fem
	Xx	1 – sA,fem – sX,femhX – sI,femhX	1 – sA,femhA – sX,femhX – sI,femhAhX	1 – sX,femhX
	xx	1 – sA,fem	1 – sA,femhA	1

A and X are incompatible alleles. Subscripts indicate selection coefficients due to autosomal fitness effects (s_A), X-linked fitness effects (s_X), and epistatic interactions (s_I). Sex-specific selection coefficients are also indicated by subscripts. Reduced fitness in double heterozygotes is assumed to be multiplicative. Dominance terms of autosomal and sex-linked loci are h_A and h_X, respectively.

Dominance terms of autosomal and sex-linked loci are h_A and h_X, respectively. For the sake of mathematical simplicity, we assume that fitness dominance terms are the same for single-locus and epistatic fitness effects. Dominance terms equal to zero imply that the incompatible allele is completely recessive to the nonincompatible allele; dominance terms equal to one imply that the incompatible allele is completely dominant. Individuals containing both A and X alleles have reduced fitness (Table 2). For example, AAXx females have a fitness 1 – s_A,fem – s_X,femh_X – s_I,femh_X. Reduced fitness in double heterozygotes is assumed to be multiplicative.

The algebra of subsequent equations is substantially more tractable if the following expressions are used:

$$A*=A_{\text{male}}{A}_{\text{fem}}+h_{\text{A}}\left(A_{\text{male}}(1-A_{\text{fem}})+A_{\text{fem}}(1-A_{\text{male}})\right)$$ (1)

$$X*=X_{\text{male}}{X}_{\text{fem}}+h_{\text{X}}\left(X_{\text{male}}(1-X_{\text{fem}})+X_{\text{fem}}(1-X_{\text{male}})\right).$$ (2)

Allele frequency changes due to selection

As in classical population genetics, allele frequencies in subsequent generations are determined by present allele frequencies and the ratio of average excess to mean fitness (Crow and Kimura 1970; Charlesworth and Charlesworth 2010). The average excess is equal to the difference between the marginal fitness of an allele and the mean fitness of a population. A general equation for allele frequency change is given by

$$\Delta p=\frac{p\text{(}w-\overline{w}\text{)}}{\overline{w}}.$$ (3)

In Equation 3, p is allele frequency, w is the marginal fitness of an allele, and $\overline{w}$ is mean fitness.

In a genetic system with synthetic incompatibilities, changes in allele frequency at one locus depend on allele frequencies at the other locus. Such dependence affects both marginal fitnesses and mean fitnesses. Allele frequency trajectories also reflect the fact that X chromosomes in males are maternally derived. As each sex can be viewed as a different selective environment, equations for allele frequency change incorporate sex-specific mean fitnesses. Mean fitnesses incorporate both the fitnesses of each genotype and the probability of observing each genotype (assuming independent assortment). We note that A* and X* terms quantify the extent that selection acts in homozygotes and heterozygotes. Mean fitnesses of males and females are

$${\overline{w}}_{\text{male}}=1-s_{\text{A,male}}A*-s_{\text{X,male}}{X}_{\text{fem}}-s_{\text{I,male}}A*X_{\text{fem}}$$ (4)

$${\overline{w}}_{\text{fem}}=1-s_{\text{A,fem}}A*-s_{\text{X,fem}}X*-s_{\text{I,fem}}A*X*.$$ (5)

Male and female changes in autosomal allele frequencies follow from the general equation for allele frequency change (Equation 3). In both sexes, marginal fitnesses of alleles are weighted by the probability that alleles are found in heterozygotes or homozygotes. Sex-specific marginal fitnesses of A alleles are

$$\begin{array}{l}{w}_{\text{A,male}}\\ =1-s_{\text{A,male}}\frac{A_{\text{male}}{A}_{\text{fem}}+A*}{A_{\text{male}}+A_{\text{fem}}}-s_{\text{X,male}}{X}_{\text{fem}}-s_{\text{I,male}}\frac{A_{\text{male}}{A}_{\text{fem}}+A*}{A_{\text{male}}+A_{\text{fem}}}{X}_{\text{fem}}\end{array}$$ (6)

$$\begin{array}{l}{w}_{\text{A,fem}}\\ =1-s_{\text{A,fem}}\frac{A_{\text{male}}{A}_{\text{fem}}+A*}{A_{\text{male}}+A_{\text{fem}}}-s_{\text{X,fem}}X*-s_{\text{I,fem}}\frac{A_{\text{male}}{A}_{\text{fem}}+A*}{A_{\text{male}}+A_{\text{fem}}}X*.\end{array}$$ (7)

Substituting the right-hand sides of the equations for mean fitness (Equations 4 and 5) and marginal fitness (Equations 6 and 7) into the general equation for allele frequency change (Equation 3) allows sex-specific changes in A allele frequencies to be generated. After grouping terms by selection coefficients,

$$\begin{array}{l}\Delta A_{\text{male,sel}}\\ =\frac{\left(A_{\text{fem}}-A_{\text{male}}\right)+s_{\text{A,male}}\left(A^{*}(2A_{\text{male}}-1)-A_{\text{male}}{A}_{\text{fem}}\right)+s_{\text{X,male}}\left(A_{\text{male}}-A_{\text{fem}}\right)X_{\text{fem}}+s_{\text{I,male}}\left(A^{*}(2A_{\text{male}}-1)-A_{\text{male}}{A}_{\text{fem}}\right)X_{\text{fem}}}{2\left(1-s_{\text{A,male}}{A}^{*}-s_{\text{X,male}}{X}_{\text{fem}}-s_{\text{I,male}}{A}^{*}{X}_{\text{fem}}\right)}\end{array}$$ (8)

$$\begin{array}{l}\Delta A_{\text{fem,sel}}\\ =\frac{\left(A_{\text{male}}-A_{\text{fem}}\right)+s_{\text{A,fem}}\left(A^{*}(2A_{\text{fem}}-1)-A_{\text{male}}{A}_{\text{fem}}\right)+s_{\text{X,fem}}\left(A_{\text{fem}}-A_{\text{male}}\right)X^{*}+s_{\text{I,fem}}\left(A^{*}(2A_{\text{fem}}-1)-A_{\text{male}}{A}_{\text{fem}}\right)X^{*}}{2\left(1-s_{\text{A,fem}}{A}^{*}-s_{\text{X,fem}}{X}^{*}-s_{\text{I,fem}}{A}^{*}{X}^{*}\right)}.\end{array}$$ (9)

Given an equal sex ratio, autosomes spend half their time in males and half in females:

$$\Delta A_{\text{sel}}=\frac{\Delta A_{\text{male,sel}}+\Delta A_{\text{fem,sel}}}{2}.$$ (10)

Male and female changes in sex-linked allele frequencies follow from Equation 3. Sex-specific marginal fitnesses of X alleles are

$$w_{\text{X,male}}=1-s_{\text{A,male}}A*-s_{\text{X,male}}-s_{\text{I,male}}A*$$ (11)

$$\begin{array}{l}{w}_{\text{X,fem}}\\ =1-s_{\text{A,fem}}A*-s_{\text{X,fem}}\frac{X_{\text{male}}{X}_{\text{fem}}+X*}{X_{\text{male}}+X_{\text{fem}}}-s_{\text{I,fem}}A*\frac{X_{\text{male}}{X}_{\text{fem}}+X*}{X_{\text{male}}+X_{\text{fem}}}.\end{array}$$ (12)

Substituting the right-hand sides of the equations for mean fitness (Equations 4 and 5) and marginal fitness (Equations 11 and 12) into the general equation for allele frequency change (Equation 3) allows sex-specific changes in X allele frequencies to be generated. After grouping terms by selection coefficients,

$$\begin{array}{l}\Delta X_{\text{male,sel}}\\ =\frac{\left(X_{\text{fem}}-X_{\text{male}}\right)+s_{\text{A,male}}{A}^{*}\left(X_{\text{male}}-X_{\text{fem}}\right)+s_{\text{X,male}}\left(X_{\text{fem}}(X_{\text{male}}-1)\right)+s_{\text{I,male}}{A}^{*}\left(X_{\text{fem}}(X_{\text{male}}-1)\right)}{1-s_{\text{A,male}}{A}^{*}-s_{\text{X,male}}{X}_{\text{fem}}-s_{\text{I,male}}{A}^{*}{X}_{\text{fem}}}\end{array}$$ (13)

$$\begin{array}{l}\Delta X_{\text{fem,sel}}\\ =\frac{\left(X_{\text{male}}-X_{\text{fem}}\right)+s_{\text{A,fem}}{A}^{*}\left(X_{\text{fem}}-X_{\text{male}}\right)+s_{\text{X,fem}}\left(X^{*}(2X_{\text{fem}}-1)-X_{\text{male}}{X}_{\text{fem}}\right)+s_{\text{I,fem}}{A}^{*}\left(X^{*}(2X_{\text{fem}}-1)-X_{\text{male}}{X}_{\text{fem}}\right)}{2\left(1-s_{\text{A,fem}}{A}^{*}-s_{\text{X,fem}}{X}^{*}-s_{\text{I,fem}}{A}^{*}{X}^{*}\right)},\end{array}$$ (14)

X chromosomes spend one-third their time in males and two-thirds of the time in females:

$$\Delta X_{\text{sel}}=\frac{\Delta X_{\text{male,sel}}+2\Delta X_{\text{fem,sel}}}{3}.$$ (15)

Allele frequency changes due to mutation

Mutation increases the frequency of A and X alleles, while selection decreases the frequency of A and X alleles. This implies that a balance between mutation and selection exists for X–autosome synthetic incompatibilities. a → A and x → X mutations are more likely when incompatible alleles are rare, leading to a form of negative frequency dependence. Allele frequency changes due to mutation are

$$\Delta A_{\text{male,mut}}=(1-A_{\text{male}}){\mu }_{\text{A}}$$ (16)

$$\Delta A_{\text{fem,mut}}=(1-A_{\text{fem}}){\mu }_{\text{A}}$$ (17)

$$\Delta X_{\text{male,mut}}=(1-X_{\text{male}}){\mu }_{\text{X}}$$ (18)

$$\Delta X_{\text{fem,mut}}=(1-X_{\text{fem}}){\mu }_{\text{X}}.$$ (19)

Overall changes in allele frequencies due to mutation incorporate the relative proportion of time that alleles spend in males or females:

$$\Delta A_{\text{mut}}=\frac{\Delta A_{\text{male,mut}}+\Delta A_{\text{fem,mut}}}{2}$$ (20)

$$\Delta X_{\text{mut}}=\frac{\Delta X_{\text{male,mut}}+2\Delta X_{\text{fem,mut}}}{3}.$$ (21)

Allele frequencies can be represented in a Cartesian plane where the x-axis refers to X-linked frequency and the y-axis refers to autosomal frequency. In contrast to single-locus dynamics, the population dynamics of an X–autosome interaction have multiple dimensions of movement. Parameter values that satisfy $\Delta A_{\text{sel}}+\Delta A_{\text{mut}}=0$ need not be parameter values that satisfy $\Delta X_{\text{sel}}+\Delta X_{\text{mut}}=0$. Thus, internal equilibria, at which both loci are polymorphic, are not guaranteed. Instead, mutation–selection balance in X–autosome systems may involve fixation of one locus. Autosomal frequencies do not change when the sum of the right-hand sides of Equations 10 and 20 is zero, and X-linked frequencies do not change when the sum of the right-hand sides of Equations 15 and 21 is zero. Mutation–selection equilibria in X–autosome systems result when both of these conditions are met (Figure 1). Simultaneously solving the nonlinear allele frequency change equations for autosomal and X-linked alleles yields equilibria conditions. However, many of these solutions do not involve valid parameter values (allele frequencies must range between 0 and 1, and individuals cannot have fitnesses that are less than zero). Because of this, the number of possible equilibria varies for different levels of dominance and selection coefficients.

Differences in Sex-Specific Allele Frequencies

When sex-linked allele frequencies differ for males and females, evolutionary trajectories can be complex. Existing single-locus theory indicates that sex-linked allele frequencies approach equilibrium via a series of damped oscillations (Crow and Kimura 1970, pp. 44–47). These dynamics also occur when there are X–autosome synthetic incompatibilities.

An understanding of sex-specific oscillations can be obtained by inspecting the leading terms in the numerators of Equations 8, 9, 13, and 14. When male allele frequencies are less than female allele frequencies, male frequencies will increase and female frequencies will decrease in the next generation. Conversely, when male frequencies are greater than female frequencies, male frequencies will decrease and female frequencies will increase in the next generation. Numerical iteration of the equations for allele frequency change reveals that sex-specific allele frequencies quickly converge via a series of damped oscillations (parameter values: $s_{\text{I,male}}=1$, $s_{\text{I,fem}}=1$, $s_{\text{A,male}}=0$, $s_{\text{A,fem}}=0$, $s_{\text{X,male}}=0$, $s_{\text{X,fem}}=0$, ${\mu }_{\text{A}}={10}^{-5}$, ${\mu }_{\text{X}}={10}^{-5}$, $h_{\text{A}}=0$, $h_{\text{X}}=0$). Even extreme initial conditions ($A_{\text{male},t=0}=1$, $A_{\text{fem},t=0}=0$, $X_{\text{male},t=0}=1$, $X_{\text{fem},t=0}=0$) result in sex-specific differences in allele frequencies that are <0.01 after 15 generations. Because sex-specific differences in allele frequency are minimal after a short number of generations, subsequent sections of this article assume that male and female allele frequencies are equal.

Synthetic Lethality in the Absence of Single-Locus Fitness Effects

The relative strength of selection depends on autosomal and sex-linked allele frequencies and dominance coefficients at both loci. For mathematical simplicity, we assume that the strength of synthetic lethality is the same for both sexes ($s_{\text{I,male}}=s_{\text{I,fem}}=s_{\text{I}}$), and mutation rates are the same at both loci (${\mu }_{\text{A}}={\mu }_{\text{X}}=\mu$). Single-locus fitness effects are assumed to be absent ($s_{\text{A,male}}=0$, $s_{\text{A,fem}}=0$, $s_{\text{X,male}}=0$, $s_{\text{X,fem}}=0$). Allele frequency trajectories for synthetic lethals are shown in Figure 2. Each panel in Figure 2 was generated by numerical iteration of the equations for allele frequency change. In Figure 2, selection can be viewed as a force pushing to the bottom left of each panel, while mutation pushes populations to the top right.

Genetic systems containing a synthetic incompatibility evolve via a two-part process. First, there is an approach to a fundamental trajectory (using the terminology of Christiansen and Frydenberg 1977). This fundamental trajectory is a set of allele frequencies that is largely independent of initial population state. Next, the system moves along this trajectory toward stable equilibria for both loci. These equilibria involve single-locus mutation–selection balance frequencies. If A is completely dominant and X is completely recessive, the population will ultimately fix the A allele (Figure 2A). If both incompatible alleles are dominant, the ultimate fate of the population depends on starting allele frequencies (Figure 2B). An internal unstable equilibrium also exists when A and X are dominant. If A is completely recessive, the population will ultimately fix the X allele (Figure 2, C and D). While along the fundamental trajectory, alleles for X–autosome incompatibilities are able to segregate at moderate frequencies. For example, if both loci have the same frequency, completely recessive synthetic lethal alleles can have allele frequencies >2% ($s=1$ and $\mu ={10}^{-5}$). Retrograde movement of allele frequencies can also occur, whereby A or X alleles initially increase in frequency only to subsequently decrease in frequency (Figure 2).

Approach to equilibrium is slow

Because increases in allele frequencies are due to mutation pressure, the approach to the fundamental trajectory and stable equilibria can be quite slow in the absence of single-locus fitness effects or genetic drift. For example, a population initially lacking A and X alleles will have allele frequencies of $A=0.0166$ and $X=0.0697$ after 20,000 generations of evolution ($s_{\text{I}}=1$, $\mu ={10}^{-5}$, $h_{\text{A}}=0$, $h_{\text{X}}=0$). Slow approaches have also been observed for synthetic incompatibilities involving pairs of autosomal loci (Christiansen and Frydenberg 1977). Finite population sizes allow for the possibility of alternative outcomes (perhaps fixing different alleles from those expected from the stable equilibria for both loci) and shorter fixation times. Monte Carlo simulations programmed in MATLAB are consistent with results from analytic theory (Figure 3).

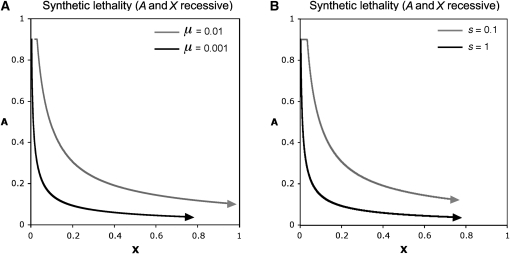
Mutation rates and strength of selection

Lower mutation rates result in fundamental trajectories with low allele frequencies (Figure 4A). Similarly, stronger selection also results in fundamental trajectories with low allele frequencies (Figure 4B). As in the one-locus case, allele frequency trajectories depend more on the ratio of mutation rate to selection coefficients than either parameter by itself. Stable equilibria for both loci also depend on the ratio of mutation rates and selection coefficients (see Equations 23 and 30). By contrast, the rate of approach to stable equilibria depends on the magnitudes of individual parameters.

Figure 4 .

Different mutation rates and selection coefficients. Synthetic lethality, equal mutation rates, and complete recessivity at both loci are assumed ($s_{\text{I,male}}=1$, $s_{\text{I,fem}}=1$, $s_{\text{A,male}}=0$, $s_{\text{A,fem}}=0$, $s_{\text{X,male}}=0$, $s_{\text{X,fem}}=0$, ${\mu }_{\text{A}}={\mu }_{\text{X}}$, $h_{\text{A}}=0$, $h_{\text{X}}=0$). Curves were generated by iterating the equations for allele frequency change for 20,000 generations. Start conditions: A_initial = 0.9, X_initial = μ/S_I. In A, different mutation rates are compared (s_I held constant at 0.1). Higher mutation rates result in faster evolutionary change along the fundamental trajectory. In B, different selection coefficients are compared (μ held constant at 0.01). Shaded curves depict $\mu /s_{\text{I}}=0.1$ and solid curves depict $\mu /s_{\text{I}}=0.01$.

Complete recessivity at both loci (synthetic lethality)

Analytic expressions for mutation–selection balance of recessive synthetic lethal alleles can be derived. For mathematical simplicity, the strength of synthetic lethality is assumed to be the same for both sexes ($s_{\text{I,male}}=s_{\text{I,fem}}=s$), and mutation rates are assumed to be the same at both loci (${\mu }_{\text{A}}={\mu }_{\text{X}}=\mu$). Single-locus fitness effects are assumed to be absent ($s_{\text{A,male}}=0$, $s_{\text{A,fem}}=0$, $s_{\text{X,male}}=0$, $s_{\text{X,fem}}=0$). Complete recessivity at both loci is also assumed ($h_{\text{A}}=h_{\text{X}}=0$). At equilibrium, the genetic load due to synthetic lethality is minimal, allowing us to assume that mean fitness is close to one. We calculate mutation–selection balance conditions separately for autosomal and sex-linked alleles and plot these values in Figure 1A.

Recalling the fact that autosomal alleles spend equal times in each sex, combining Equations 8–10 allows Equation 22 to be generated. The net change in autosome frequencies due to completely recessive synthetic lethality is

$$\Delta A_{\text{sel}}=\frac{-s_{\text{I}}{A}^2(1-A)X(1+X)}{2}.$$ (22)

Autosomal mutation–selection balance occurs when $\Delta A_{\text{sel}}+\Delta A_{\text{mut}}=0$. We combine Equations 20 and 22 to obtain mutation–selection balance frequencies for autosomal alleles. Given complete recessivity and synthetic lethality, mutation–selection balance of autosomal alleles occurs when

$$\frac{\mu }{s_{\text{I}}}=\frac{A^{2}X(1+X)}{2}.$$ (23)

Recalling the fact that one-third of X chromosomes are present in males and two-thirds of X chromosomes are present in females, combining Equations 13–15 allows Equation 24 to be generated. The net change in sex-linked frequencies due to completely recessive synthetic lethality is

$$\Delta X_{\text{sel}}=\frac{-s_{\text{I}}{A}^{2}X(1-X)(1+2X)}{3}.$$ (24)

Sex-linked mutation–selection balance occurs when $\Delta X_{\text{sel}}+\Delta X_{\text{mut}}=0$. We combine Equations 21 and 24 to obtain mutation–selection balance frequencies for sex-linked alleles. Given complete recessivity and synthetic lethality, mutation–selection balance of sex-linked alleles occurs when

$$\frac{\mu }{s_{\text{I}}}=\frac{A^{2}X(1+2X)}{3}.$$ (25)

Are there any conditions that satisfy mutation–selection balance for both autosomal and sex-linked alleles? In Figure 1A, the autosomal mutation–selection balance curve is always below the sex-linked mutation–selection balance curve. This implies that the X allele will ultimately be fixed. Minor discrepancies between the positions of internal equilibria in Figures 1, 2, and 5 arise because Figure 1 assumes that allele frequencies are the same in both sexes. The transitive property of equality allows autosomal and sex-linked mutation–selection balance equations (Equations 23 and 25) to be combined:

$$\frac{A^{2}X(1+X)}{2}=\frac{A^{2}X(1+2X)}{3}.$$ (26)

Equation 26 is satisfied when X = 1. This indicates that complete recessivity at both loci is expected to ultimately result in a population that is fixed for the X allele. This is consistent with the evolutionary trajectories of synthetic lethal alleles in Figure 2C.

Complete dominance at both loci (synthetic lethality)

Analytic expressions for mutation–selection balance of dominant synthetic lethal alleles can also be derived. The strength of synthetic lethality is assumed to be the same for both sexes, and mutation rates are assumed to be the same at both loci. Complete dominance at both loci is assumed ($h_{\text{A}}=h_{\text{X}}=1$). Mutation–selection balance conditions were calculated separately for autosomal and sex-linked alleles and plotted in Figure 1B. Because $\overline{w}$ can often deviate substantially from one when dominant alleles are present, equations in this subsection incorporate mean fitness terms.

Recalling the fact that autosomal alleles spend equal times in each sex, combining Equations 8–10 yields Equation 27. The net change in autosome frequencies due to completely dominant synthetic lethality is

$$\Delta A_{\text{sel}}=\frac{-s_{\text{I}}A{(1-A)}^{2}X\left((2-X){\overline{w}}_{\text{male}}+{\overline{w}}_{\text{fem}}\right)}{2{\overline{w}}_{\text{male}}{\overline{w}}_{\text{fem}}}.$$ (27)

We combine Equations 20 and 27 to obtain mutation–selection balance frequencies for autosomal alleles. Given complete dominance and synthetic lethality, mutation–selection balance of autosomal alleles occurs when the following nonlinear equation is satisfied:

$$\frac{\mu }{s_{\text{I}}}=\frac{A(1-A)X\left((2-X){\overline{w}}_{\text{male}}+{\overline{w}}_{\text{fem}}\right)}{2{\overline{w}}_{\text{male}}{\overline{w}}_{\text{fem}}}.$$ (28)

Recalling the fact that one-third of X chromosomes are present in males and two-thirds of X chromosomes are present in females, combining Equations 13–15 yields Equation 29. The net change in sex-linked frequencies due to completely dominant synthetic lethality is

$$\Delta X_{\text{sel}}=\frac{-s_{\text{I}}A(2-A)X(1-X)\left(2(1-X){\overline{w}}_{\text{male}}+{\overline{w}}_{\text{fem}}\right)}{3{\overline{w}}_{\text{male}}{\overline{w}}_{\text{fem}}}.$$ (29)

We combine Equations 21 and 29 to obtain mutation–selection balance frequencies for sex-linked alleles. Given complete dominance and synthetic lethality, mutation–selection balance of sex-linked alleles occurs when a nonlinear equation is satisfied:

$$\frac{\mu }{s_{\text{I}}}=\frac{A(2-A)X\left(2(1-X){\overline{w}}_{\text{male}}+{\overline{w}}_{\text{fem}}\right)}{3{\overline{w}}_{\text{male}}{\overline{w}}_{\text{fem}}}.$$ (30)

In Figure 1B, autosomal and sex-linked equilibria curves cross at a single point. This unstable internal equilibrium involves a population with low frequencies of the A allele and moderate frequencies of the X allele.

Synthetic Sterility in the Absence of Single-Locus Effects

Under synthetic sterility, selection acts only in a single sex ($s_{\text{I,fem}}=0$ when male sterility is present and $s_{\text{I,male}}=0$ when female sterility is present). The relative strength of selection depends on autosomal frequencies, sex-linked allele frequencies, and dominance coefficients. Two-thirds of the X chromosomes in a population are found in females, in contrast to one-half the autosomes. This suggests that allele frequency trajectories of autosomal and sex-linked alleles will differ when synthetic sterility is present. Using the same mathematical techniques as in the Complete dominance at both loci (synthetic lethality) section, we derive equations for synthetic male sterility (Appendix A) and synthetic female sterility (Appendix B). Allele frequency trajectories for synthetic sterile alleles are shown in Figure 5. Each panel in Figure 5 was generated by numerical iteration of the equations for allele frequency change.

The dynamics of synthetic sterile alleles are broadly similar to those of synthetic lethal alleles: allele frequency changes involve approaches to fundamental trajectories and stable equilibria. Because selection acts only in one sex, segregating allele frequencies of sterile alleles are slightly higher than expected under synthetic lethality. Once again, approaches to stable equilibria are slow.

Synthetic Load and Sex-Specific Reductions in Fitness

Populations containing synthetic incompatibilities have lower mean fitness than populations that lack these alleles. This is a form of genetic load (Whitlock and Bourguet 2000). Synthetic load is defined here as the amount that a population’s fitness is below maximum due to synthetic incompatibilities. This term can be applied to individuals or populations. If synthetic incompatibilities involve X chromosomes and autosomes, synthetic load can be unequal for males and females.

Synthetic load is expected to be greater for males if synthetic lethal alleles are recessive. This is because the effects of deleterious X-linked alleles are not masked in hemizygous males. However, the opposite pattern is observed for dominant synthetic lethal alleles. In this scenario, each X chromosome in females can potentially contain a deleterious allele. Autosomal frequencies do not influence the relative proportion of synthetic load in males or females. Substituting the equations for sex-specific mean fitnesses allows an equation for the male proportion of synthetic load to be derived. We assume that selection coefficients are the same for both sexes:

$$\begin{array}{l}\frac{1-{\overline{w}}_{\text{male}}}{(1-{\overline{w}}_{\text{male}})+(1-{\overline{w}}_{\text{fem}})}\\ =\frac{s_{\text{A}}A*+s_{\text{X}}{X}_{\text{fem}}+s_{I}A*X_{\text{fem}}}{2s_{\text{A}}A*+s_{\text{X}}(X_{\text{fem}}+X*)+s_{\text{I}}A*(X_{\text{fem}}+X*)}.\end{array}$$ (31)

Because we are focusing on the proportion of load that is due to synthetic lethality, we set s_A and s_x terms equal to zero. Assuming that allele frequencies are the same in each sex,

$$\text{Proportion of synthetic load in males}=\frac{1}{1+X+2h_{\text{X}}(1-X)}.$$ (32)

Solving for $h_{\text{X}}=0$ and $h_{\text{X}}=1$ gives the male proportion of synthetic load for recessive and dominant alleles:

$$\text{Proportion of synthetic load in males }(h_{\text{X}}=0) =\frac{1}{1+X}.$$ (33)

$$\text{Proportion of synthetic load in males }(h_{\text{X}}=1)=\frac{1}{3-X}.$$ (34)

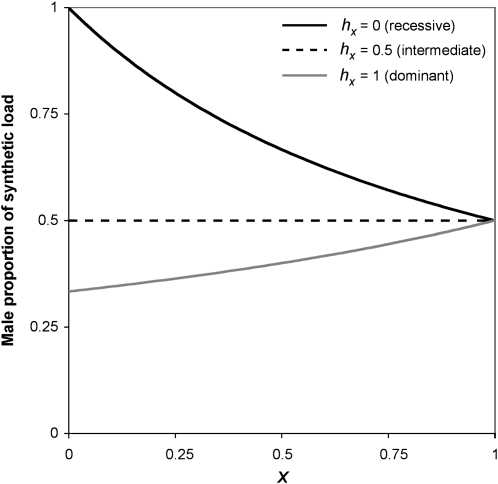
When dominance is intermediate on an additive scale (h_A = 0.5), synthetic load is equal for males and females (Figure 6). Recessive synthetic lethality results in an excess of male lethality, and dominant synthetic lethality results in an excess of female lethality. These effects are magnified when frequencies of the X allele are low. This dependence of sex-specific effects on dominance coefficients has been well studied in the Haldane’s rule literature (Orr 1993b; Turelli and Orr 1995, 2000).

Figure 6 .

Male proportion of synthetic load for different levels of X-linked dominance. Synthetic load refers to the amount that a population’s fitness is below maximum due to synthetic incompatibilities. Three levels of X-linked dominance are considered: complete recessivity (shaded line), intermediate dominance (dashed solid line), and complete dominance (solid line). Autosomal dominance does not influence the proportion of synthetic load that is male or female.

Synthetic Incompatibilities in the Presence of Single-Locus Fitness Effects

Synthetic lethality Wwth single-locus fitness effects

While previous sections have focused on epistatic fitness interactions, many alleles also have single-locus fitness effects. This is important because the magnitudes of selection coefficients are often larger than mutation rates (Gillespie 1991; Charlesworth and Charlesworth 2010). Because of this, genetic systems containing epistatic interactions and single-locus fitness effects are more likely to have allele frequencies that reflect a balance between different selective forces than a balance between mutation and selection. In Figure 7 synthetic lethality pushes allele frequencies downward and leftward while single-locus fitness effects push allele frequencies upward and to the right. Beneficial single-locus fitness effects allow incompatible alleles to segregate at higher frequencies (compare Figures 2 and 7). Equations 8–10 and 13–15 and a series of simplifying assumptions allow equations for selection-induced allele frequency changes to be derived. For mathematical simplicity we assume that allele frequencies and selection coefficients are the same for both sexes. If synthetic lethality is completely recessive,

$$\begin{array}{l}\Delta A_{\text{sel,recessive}}\\ =\frac{-A^2\left(1-A\right)}{2{\overline{w}}_{\text{male}}{\overline{w}}_{\text{fem}}}\left[s_{\text{A}}({\overline{w}}_{\text{male}}+{\overline{w}}_{\text{fem}})+s_{\text{I}}X\left(X{\overline{w}}_{\text{male}}+{\overline{w}}_{\text{fem}}\right)\right]\end{array}$$ (35)

$$\begin{array}{l}\Delta X_{\text{sel,recessive}}\\ =\frac{-X(1-X)}{3{\overline{w}}_{\text{male}}{\overline{w}}_{\text{fem}}}\left[s_{\text{X}}\left(2X{\overline{w}}_{\text{male}}+{\overline{w}}_{\text{fem}}\right)+s_{\text{I}}{A}^2\left(2X{\overline{w}}_{\text{male}}+{\overline{w}}_{\text{fem}}\right)\right].\end{array}$$ (36)

Allele frequency changes due to single-locus and epistatic fitness effects of completely dominant alleles are

$$\begin{array}{l}\Delta A_{\text{sel,dominant}}\\ =\frac{-A{\left(1-A\right)}^2}{2{\overline{w}}_{\text{male}}{\overline{w}}_{\text{fem}}}\left[s_{\text{A}}({\overline{w}}_{\text{male}}+{\overline{w}}_{\text{fem}})+s_{\text{I}}X\left((2-X){\overline{w}}_{\text{male}}+{\overline{w}}_{\text{fem}}\right)\right].\end{array}$$ (37)

$$\begin{array}{l}\Delta X_{\text{sel,dominant}}\\ =\frac{-X(1-X)}{3{\overline{w}}_{\text{male}}{\overline{w}}_{\text{fem}}}[s_{\text{X}}\left(2\left(1-X\right){\overline{w}}_{\text{male}}+{\overline{w}}_{\text{fem}}\right)\\ +s_{\text{I}}A(2-A)\left(2\left(1-X\right){\overline{w}}_{\text{male}}+{\overline{w}}_{\text{fem}}\right)].\end{array}$$ (38)

Similar calculations can also be made for synthetic sterility in the presence of single-locus fitness effects (data not shown).

Deleterious single-locus fitness effects for both incompatible alleles

If both A and X alleles have deleterious single-locus effects, joint allele frequencies are unlikely to be high enough for synthetic incompatibilities to have an appreciable effect. In this scenario, mutation–selection balance frequencies are expected to simply follow single-locus expectations:

$$\widehat{A}=\frac{2{\mu }_{\text{A}}}{(s_{\text{X,male}}+s_{\text{X,fem}})h_{\text{A}}}\text{, }\widehat{X}=\frac{3{\mu }_{\text{X}}}{s_{\text{A,male}}+2s_{\text{A,fem}}{h}_{\text{X}}}.$$ (39)

Beneficial single-locus fitness effects for a single incompatible allele

The incompatible allele with beneficial single-locus fitness effects is able to reach fixation while the other incompatible allele is maintained at mutation–selection balance frequencies. Equilibrium allele frequencies when the A allele is beneficial ($s_{\text{A}}<0$ and $s_{\text{X}}=0$) are

$$\widehat{A}=1, \widehat{X}=\frac{3{\mu }_{\text{X}}}{(s_{\text{A,male}}+s_{\text{I,male}})+2(s_{\text{A,fem}}+s_{\text{I,fem}})h_{\text{X}}}.$$ (40)

Equilibrium allele frequencies when the X allele is beneficial ($s_{\text{A}}=0$ and $s_{\text{X}}<0$) are

$$\widehat{A}=\frac{2{\mu }_{\text{A}}}{(s_{\text{X,male}}+s_{\text{I,male}})h_{\text{A}}+(s_{\text{X,fem}}+s_{\text{I,fem}})h_{\text{A}}}, \widehat{X}=1.$$ (41)

Beneficial alleles at both loci

When synthetic lethal alleles at both loci have beneficial single-locus fitness effects, equilibrium allele frequencies are determined by the type of epistasis that is present (either magnitude or sign epistasis). Magnitude epistasis involves alleles that are always beneficial or deleterious (Weinreich et al. 2005). Beneficial single-locus fitness effects can overcome synthetic incompatibilities when magnitude epistasis is present. This scenario results in a trivial equilibrium with both A and X reaching fixation. By contrast, sign epistasis means that an allele is beneficial on one genetic background and deleterious on another genetic background (Weinreich et al. 2005). Sign epistasis at both loci results in dynamics in which the incompatible allele that fixes first is maintained at high frequency, while the other incompatible allele is able to persist only at low frequencies (i.e., historical contingency matters).

For a new mutation to reach fixation it must avoid stochastic loss, a property that is largely determined by the initial fitnesses of alleles. The fitness effects of rare dominant alleles are seen regardless of whether the alleles are autosomal or X-linked. However, the fitness effects of rare recessive alleles are observed only if they are X-linked (because of hemizygous males). The rate that alleles fix in a population has been termed fixation flux (Otto and Whitlock 1997). By comparing the magnitudes of fitness flux at autosomal and X-linked loci, we can obtain the probability that A or X alleles reach fixation first. We assume that populations initially contain only a and x alleles and that populations are in the strong selection–weak mutation regime (Gillespie 1991). The fixation flux of autosomal loci is found by multiplying the number of new mutants per generation ($2N_{\text{e}}\mu$) by the probability of fixation of each mutant ($2s_{\text{A}}{h}_{\text{A}}$):

$$\text{Fixation flux of }A\text{ alleles =}\hspace{0.17em}4N_{\text{e}}{\mu }_{\text{A}}{s}_{\text{A}}{h}_{\text{A}}.$$ (42)

The fixation flux of X alleles is weighted by the probability that alleles are found in males or females and by the dominance coefficient of X alleles:

$$\text{Fixation flux of }X\text{ alleles}=N_{\text{e}}{\mu }_x{s}_x(2h_{\text{X}}+1).$$ (43)

Combining Equations 42 and 43 yields the relative probability that A fixes first:

$$\text{Probability that }A\text{ fixes before }X\hspace{0.17em}= \frac{4{\mu }_{\text{A}}{s}_{\text{A}}{h}_{\text{A}}}{4{\mu }_{\text{A}}{s}_{\text{A}}{h}_{\text{A}}+{\mu }_x{s}_x(2h_{\text{X}}+1)}.$$ (44)

If $s_{\text{A}}=s_{\text{X}}$ and mutation rates are the same at both loci, Equation 44 reduces to

$$\text{Probability that }A\text{ fixes before }X\hspace{0.17em}= \frac{4h_{\text{A}}}{4h_{\text{A}}+2h_{\text{X}}+1}.$$ (45)

This equation indicates that autosomal alleles are more likely to fix first if alleles are dominant and X-linked alleles are more likely to fix first if alleles are recessive. Specifically, if there is complete dominance, there is a four out of seven chance (∼57%) that A alleles will fix before X alleles. This occurs because of differences in the relative number of copies of autosomal and X-linked alleles. By contrast, complete recessivity results in X alleles fixing before A alleles (as long as population size is large). This is because the effects of recessive X-linked alleles are unmasked in hemizygous males. Equation 45 is consistent with previous findings (Charlesworth et al. 1987), and computer simulations confirm the validity of this equation (see Table 3).

Table 3 . Synthetic lethality in the presence of beneficial single-locus effects.

Synthetic lethality scenario	P (A fixes first): theory	P (A fixes first): simulation
Beneficial A, intermediate dominance at both loci: $s_{\text{A}}=-0.1, s_{\text{X}}=0, s_{\text{I}}=1, h_{\text{A}}=0.5, h_{\text{X}}=0.5$	1.000	1.000 (0.998–1.000)
Beneficial X, intermediate dominance at both loci: $s_{\text{A}}=0, s_{\text{X}}=-0.1, s_{\text{I}}=1, h_{\text{A}}=0.5, h_{\text{X}}=0.5$	0.000	0.000 (0.000–0.002)
Beneficial A and X, complete recessivity at both loci: $s_{\text{A}}=-0.1, s_{\text{X}}=-0.1, s_{\text{I}}=1, h_{\text{A}}=0, h_{\text{X}}=0$	0.000	0.098 (0.080–0.118)
Beneficial A and X, weak dominance at both loci: $s_{\text{A}}=-0.1, s_{\text{X}}=-0.1, s_{\text{I}}=1, h_{\text{A}}=0.25, h_{\text{X}}=0.25$	0.400	0.392 (0.362–0.422
Beneficial A and X, intermediate dominance at both loci: $s_{\text{A}}=-0.1, s_{\text{X}}=-0.1, s_{\text{I}}=1, h_{\text{A}}=0.5, h_{\text{X}}=0.5$	0.500	0.508 (0.477–0.538)
Beneficial A and X, complete dominance at both loci: $s_{\text{A}}=-0.1, s_{\text{X}}=-0.1, s_{\text{I}}=1, h_{\text{A}}=1, h_{\text{X}}=1$	0.571	0.563 (0.532–0.594)
Beneficial A and X, A dominant and X recessive: $s_{\text{A}}=-0.1, s_{\text{X}}=-0.1, s_{\text{I}}=1, h_{\text{A}}=1, h_{\text{X}}=0$	0.800	0.812 (0.787–0.836)
Beneficial A and X, A recessive and X dominant: $s_{\text{A}}=-0.1, s_{\text{X}}=-0.1, s_{\text{I}}=1, h_{\text{A}}=0, h_{\text{X}}=1$	0.000	0.027 (0.018–0.594)

MATLAB simulations were run until either the A or the X allele reached fixation, and computer simulations were run 1000 times for each set of parameter values with population sizes of 1000 individuals. Selection coefficients were chosen to be the same for both sexes, and mutation rates were chosen to be the same for both loci ($\mu ={10}^{-5}$). Values in parentheses indicate 95% confidence intervals (Agresti and Coull 1998).

Discussion

Comparisons with other types of incompatibilities

X–autosome incompatibilities segregate along a fundamental trajectory before ultimately fixing one locus, the identity of which is largely determined by the type of fitness dominance. As is the case for autosome–autosome synthetic incompatibilities, X–autosome incompatibilities are able to segregate at much higher frequencies than single-locus expectations. Setting A = X, fundamental trajectories give frequencies that are on the order of $\sqrt[2]{\mu /s}$ when both incompatible alleles are dominant, $\sqrt[3 ]{\mu /s}$ when one incompatible allele is dominant, and $\sqrt[4 ]{\mu /s}$ when both incompatible alleles are recessive. Stable equilibria for X–autosome incompatibilities are also biased toward fixation of alleles at X-linked or autosomal loci (with the particular locus depending on fitness dominance). This is in contrast to autosome–autosome theory, which has symmetric expectations as long as mutation rates at both loci are equal (Christiansen and Frydenberg 1977). One reason these patterns arise is because of differences in mutation pressure between X-linked and autosomal loci. Another reason is that X-linkage yields greater selection in males when alleles are recessive and reduced selection in males when alleles are dominant.

When synthetic lethal and sterile alleles also confer single-locus fitness effects, historical contingency matters. This is because an incompatible allele that is able to reach high frequency can inhibit the other incompatible allele from reaching high frequency. Autosomal alleles are more likely to reach fixation first if fitness effects are dominant, and X-linked alleles are more likely to reach fixation first if fitness effects are recessive. It is currently unknown whether most synthetic lethal alleles also have single-locus fitness effects. Data from double-mutant screens in S. cerevisiae are mixed: although many synthetic lethal combinations involve alleles with negligible single-locus effects, the magnitudes of single-locus and epistatic fitness effects are positively correlated (Costanzo et al. 2010). At present, both scenarios are plausible: synthetic incompatibilities can involve alleles that are otherwise neutral (Figures 1–5), or synthetic incompatibilities can involve alleles that also have single-locus fitness effects (Figure 7).

Synthetic lethality vs. synthetic sterility

Technically, male sterility and female sterility scenarios also apply to situations in which there is sex-specific lethality. However, empirical evidence suggests that sex-specific incompatibilities will usually involve sterility rather than lethality. For instance, mutagenesis studies in D. melanogaster show that lethal mutations usually affect both sexes more or less equally, but sterility mutations are largely sex specific (Lindsley and Tokuyasu 1980; Mahowald and Kambysellis 1980; Wu and Davis 1993). Epistatic interactions that reduce viability are likely to have the same effect in both sexes, while incompatibilities that disrupt the reproductive system of one sex need not disrupt the reproductive system of the other sex.

The salient difference between synthetic lethality and synthetic sterility is that selection is stronger for the former because both sexes are affected. This allows synthetic sterile alleles to segregate at higher frequencies. These effects are similar to situations in which genes are conditionally expressed (Van Dyken and Wade 2010). Another difference is that autosomal dominance coefficients affect all types of synthetic incompatibilities, while X-linked dominance coefficients affect only synthetic lethality and synthetic female sterility. In males, each selection event removes two autosomal alleles and one X-linked allele. By contrast, each selective event removes two autosomal alleles and two X-linked alleles in females. Because of this, the relative amount that autosomal and sex-linked alleles are purged depends on whether selection acts in males, females, or both sexes. In contrast to selection, mutation pressure is independent of the type of synthetic incompatibility. This is because female sterile mutations can arise in males, only to be passed on to their daughters (and vice versa).

Cryptic synthetic incompatibilities

Synthetic lethal and sterile alleles may masquerade as single-locus effects. This is because stable equilibria involve fixation at one locus and low-frequency variation at the other locus. Allele frequencies at the other locus follow single-locus mutation–selection balance expectations. Just because alleles are found at single-locus mutation–selection frequencies does not mean that they lack fitness interactions with alleles at other loci. This finding parallels the partitioning of variance in quantitative genetics: populations fixed for one locus will fail to show statistical epistasis even though there is functional epistasis (Wade 1992; Templeton 2000).

An additional implication of this work is that cryptic incompatibilities are likely to be biased in a particular direction. If X–autosome synthetic lethality involves recessive alleles, the autosomal locus is expected to be polymorphic and the X-linked locus is expected to be fixed for the X allele. By contrast, dominant X–autosome synthetic lethality in the absence of single-locus fitness effects yields fixation of A alleles and polymorphism at the X-linked locus. Exceptions to these patterns can occur in small populations. In addition, synthetic sterility results in different patterns from synthetic lethality (compare Figures 2 and 5).

Divergent populations, Haldane’s rule, and speciation

If divergent allopatric populations have different frequencies of incompatible autosomal and X-linked alleles, secondary contact can result in populations with high levels of genetic load. This is most striking if one population is fixed for the A allele and the other population is fixed for the X allele. At least four mechanisms can enable this: genetic drift coupled with low mutation rates in small populations, population-specific dominance modification, historical contingency involving single-locus fitness effects, and population-specific selection.

Even prior to divergence, single populations can have asymmetric levels of reduced fitness in males and females. The driving issue here is whether X-linked factors are recessive or dominant. The extent to which male-biased synthetic incompatibilities are present depends on two elements: the overall amount of synthetic load (which is maximized when both alleles segregate at moderate frequencies) and the proportion of load that occurs in males (which is maximized when X-linked incompatibilities are rare and recessive). With X–autosome incompatibilities, Haldane’s rule-like patterns can occur prior to speciation. Importantly, Equation 32 gives testable predictions that can be assayed in model systems such as Drosophila.

The overall impact of X–autosome interactions depends on the proportion of the genome that is X-linked. Not surprisingly, the size of the X chromosome and thus the relative importance of X–autosome interactions also affect Haldane’s rule and associated phenomena of speciation (Turelli and Begun 1997). Regardless, X–autosome synthetic incompatibilities are an important evolutionary phenomenon that affects both allele frequency trajectories within populations and allele frequency differences between populations (Presgraves 2008).

Appendix A: Synthetic Male Sterility

Synthetic male sterility refers to situations in which epistatic fitness effects are present in males and absent in females ($s_{\text{I,male}}>0$ and $s_{\text{I,fem}}=0$.) We assume that single-locus fitness effects are absent and mutation rates are the same at both loci:

$$\Delta A_{\text{sel, recessive male sterility}}=\frac{-s_{\text{I,male}}{A}^2(1-A)X}{2}.$$ (A1)

Conditions for mutation–selection balance of recessive autosomal alleles are

$$\frac{\mu }{s_{\text{I,male}}}=\frac{A^{2}X}{2}$$ (A2)

$$\Delta X_{\text{sel, recessive male sterility}}=\frac{-s_{\text{I,male}}{A}^{2}X(1-X)}{3}.$$ (A3)

Conditions for mutation–selection balance of recessive sex-linked alleles are

$$\frac{\mu }{s_{\text{I,male}}}=\frac{A^{2}X}{3}$$ (A4)

$$\Delta A_{\text{sel, dominant male sterility}}=\frac{-s_{\text{I,male}}A{(1-A)}^{2}X}{2{\overline{w}}_{\text{male}}}.$$ (A5)

Conditions for mutation–selection balance of dominant autosomal alleles are

$$\frac{\mu }{s_{\text{I,male}}}=\frac{A(1-A)X}{2{\overline{w}}_{\text{male}}}$$ (A6)

$$\Delta X_{\text{sel, dominant male sterility}}=\frac{-s_{\text{I,male}}A(2-A)X\left(1-X\right)}{3{\overline{w}}_{\text{male}}}.$$ (A7)

Conditions for mutation–selection balance of dominant sex-linked alleles are

$$\frac{\mu }{s_{\text{I,male}}}=\frac{A(2-A)X}{3{\overline{w}}_{\text{male}}}.$$ (A8)

Appendix B: Synthetic Female Sterility

Synthetic female sterility refers to situations in which epistatic fitness effects are present in females and absent in males ($s_{\text{I,fem}}>0$ and $s_{\text{I,male}}=0$.) We assume that single-locus fitness effects are absent and mutation rates are the same at both loci:

$$\Delta A_{\text{sel, recessive female sterility}}=\frac{-s_{\text{I,fem}}{A}^2(1-A)X^2}{2}.$$ (B1)

Conditions for mutation–selection balance of recessive autosomal alleles are

$$\frac{\mu }{s_{\text{I,fem}}}=\frac{A^2{X}^2}{2}$$ (B2)

$$\Delta X_{\text{sel, recessive female sterility}}=\frac{-2s_{\text{I,fem}}{A}^2{X}^2(1-X)}{3}.$$ (B3)

Conditions for mutation–selection balance of recessive sex-linked alleles are

$$\frac{\mu }{s_{\text{I,fem}}}=\frac{2A^2{X}^2}{3}$$ (B4)

$$\Delta A_{\text{sel, dominant female sterility}}=\frac{-s_{\text{I,fem}}A{(1-A)}^{2}X(2-X)}{2{\overline{w}}_{\text{fem}}}.$$ (B5)

Conditions for mutation–selection balance of dominant autosomal alleles are

$$\frac{\mu }{s_{\text{I,fem}}}=\frac{A(1-A)X(2-X)}{2{\overline{w}}_{\text{fem}}}$$ (B6)

$$\Delta X_{\text{sel, dominant female sterility}}=\frac{-2s_{\text{I,fem}}A(2-A)X{(1-X)}^2}{3{\overline{w}}_{\text{fem}}}.$$ (B7)

Conditions for mutation–selection balance of dominant sex-linked alleles are

$$\frac{\mu }{s_{\text{I,fem}}}=\frac{2A(2-A)X(1-X)}{3{\overline{w}}_{\text{fem}}}.$$ (B8)