Figure 4.

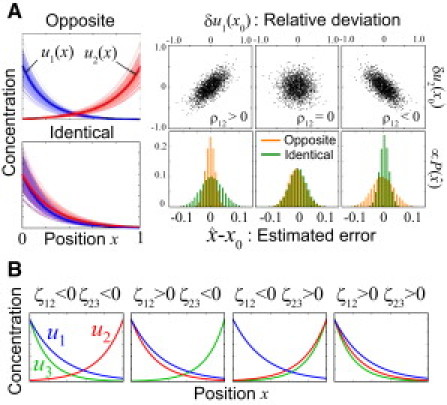
Optimal encoding design for one-dimensional positioning. (A) Optimal encoding for two morphogens (M = 2). For positively correlated noises, the oppositely directed gradients are better than identically directed gradients, and vice versa for negatively correlated noises. (Left) (Blue and red curves) Variability of morphogen gradients over 150 embryos. (Bold curves) Average profiles are u₁(x) = exp(−5x), u₂(x) = exp(4(x − 1)) (upper left), and u₂ (x) = exp(−4x) u₂ (x) = exp(−4x) (lower leftt). As a noise source, we assumed the variability of the morphogen source levels that obeys two-variable Gaussian distribution, where the SD was set as σ₁ = σ₂ = 0.2. (Upper right) When the variability of the morphogen source levels are correlated with each other, the concentrations of the two morphogens (u₁′, u₂′) observed at any position x₀ are also correlated with each other, where the correlation coefficient is denoted by ρ₁₂. The upper right panels show the distributions of the relative deviations of concentrations from their averages at x₀, δu_i(x₀) ≡ u′_i/u_i (x₀) −1. ρ₁₂ = 0.7 (left) and ρ₁₂ = −0.7 (right). (Lower right) The histograms (∝$P\left(\hat{x}\right)$) of the estimated error relative to the organ size. It becomes sharper when the appropriate choice of relative directions of gradients is made in the presence of correlation (ρ ≠ 0). (B) Optimal encoding for three morphogens when inequality |ζ₁₂| > |ζ₂₃| > |ζ₃₁| holds (see the text for the definition of ζ_ij). The direction of a morphogen gradient is fixed as u₁ (x) = exp(−5x). The directions for the rest two are u₂ (x) = exp(−4x) or u₂ (x) = exp(4(x − 1)) for the second morphogen, and u₃ (x) = exp(−3x) or u₃ (x) = exp(3(x − 1)) for the third morphogen. Parameters: (|η₁|, |η₂|, |η₃|) = (50, 40, 30) for PP values and (σ₁, σ₂, σ₃, ρ₁₂, ρ₂₃, ρ₃₁) = (0.1, 0.1, 0.1, ±0.5, ±0.5, 0) for the variability of morphogen source levels.