Figure 5.

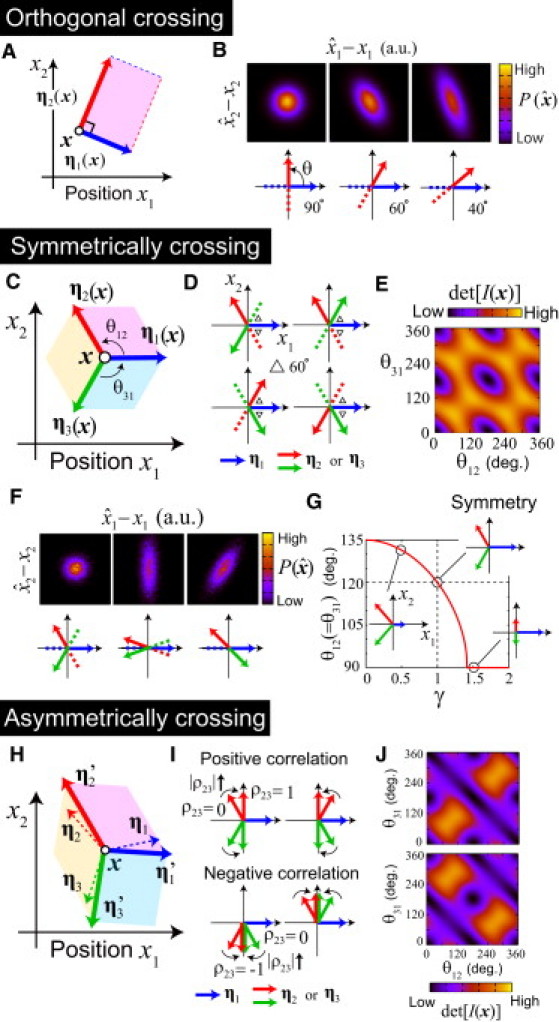
Optimal encoding designs for two-dimensional positioning. (A and B) Orthogonal morphogen gradient vectors is the optimal encoding in the absence of informational redundancy (M = N). In this case, ML decoding (${\hat{\mathit{x}}}_{ML}$) becomes the natural decoding (u⁻¹ (x)). Distribution of $P\left(\hat{\mathit{x}}\right)$ was calculated for the case with grad u₁ (x) = (1,0), grad u₂ (x) = (cos θ, sin θ), σ₁ (x) = σ₂ (x), and ρ₁₂ (x) = 0 at a focal location x. $P\left(\hat{\mathit{x}}\right)$ is the sharpest for the orthogonal crossing. (C–J) Encoding designs in the presence of informational redundancy (M > N). When different morphogens have the same PP and their noises are independent, (C) symmetrically crossing gradient vectors gives the best encoding. (D) Eight possible encoding rules to achieve maximal precision, and (E) dependence of the precision and (F) that of $P\left(\hat{\mathit{x}}\right)$ on the angles between gradient vectors in the case of (N,M) = (2,3). (E) The value det[I(x)] was calculated for the case with η₁ = (1,0), η₂ = (cos θ₁₂, sin θ₁₂), and η₃ = (cos (−θ₃₁), sin (−θ₃₁)). (F) $P\left(\hat{\mathit{x}}\right)$ is shown for the cases with (θ₁₂,θ₃₁) = (120°, 120°) (left), (θ₁₂,θ₃₁) = (160°, 160°) (middle), and (θ₁₂,θ₃₁) = (135°, 45°) (right). When different morphogens have different PP or when their noises are correlated, (H) the best encoding is no longer the symmetrical arrangement. (G) In the case of ‖η₁‖ = γ ‖η₂‖ = γ ‖η₃‖ and ρ₁₂ = ρ₂₃ = ρ₃₁ = 0, for γ >> 1, the maximum precision is achieved when the angle between the gradient vectors of morphogens 1 and 2 (or 3) is 90°; for γ << 1, the best encoding is when the angle of gradient vectors of morphogens 2 and 3 approaches 90°. The relative orientations of gradient vectors are shown for the cases of γ = 0.5, 1.0, 1.5. (I) When ‖η₁‖ = ‖η₂‖ = ‖η₃‖, ρ₁₂ = ρ₃₁ = 0, and ρ₂₃ ≠ 0, the optimal angle between the gradient vectors of morphogens with uncorrelated noises approaches 90° as |ρ₂₃| increases. (J) Dependence of the precision on the angles in the case of ρ₂₃ = ±0.8. In the calculation of det[I(x)], we assume η₁ = (1,0), η₂ = (cos θ₁₂, sin θ₁₂), and η₃ = (cos(−θ₃₁), sin(−θ₃₁)).