Figure 6.

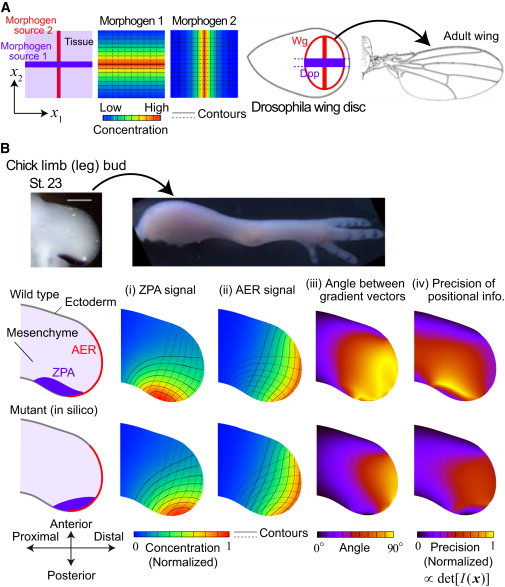
Spatial dependence of local precision and global optimality of encoding in two-dimensional positioning by two morphogens. (A) (Left) When the two morphogens have linear sources crossing orthogonally with each other, their gradient vectors also cross orthogonally everywhere in a tissue. (Right) This idea appears to be adopted in the case of Dpp and Wg in the wing disk during the development of Drosophila embryo. (B) When the shapes of morphogen sources and tissue boundaries have curvature, the contours of morphogen concentrations also become curved. The spatial pattern of the angle between gradient vectors strongly depends on those shapes and the arrangement of locations of morphogen sources. In the vertebrate limb development (Top, chick limb bud), the angle between the gradient vectors of two signals from typical information sources, ZPA and AER, is nearly orthogonal in a wide range of the tissue for the wild-type (middle), whereas the orthogonality is lost remarkably if an information source is perturbed (bottom). This implies that the encoding is optimized to improve the global precision Ψ_Ω (see Eq. 10). (Middle and bottom panels) In panels (i) and (ii), we calculated the spatial patterns of ZPA and AER signals by assuming diffusion and linear degradation, ∂u_i/∂t = DΔu_i − γu_i with zero-flux boundary condition except for the proximal end for which the signal level is assumed to be zero. We also assumed constant influx from ZPA and AER. The shapes of contours do not depend on parameters (i.e., diffusion constant (D), degradation rate (γ), and the levels of signal influx). Real organ geometry was used by tracing the picture shown in the top panels. In panel (iv), σ_i (x) ∝ u_i (x) was assumed, where the proportionality constant is independent of x.