Millisecond-Scale Biochemical Response to Change in Strain

Abstract

Muscle fiber contraction involves the cyclical interaction of myosin cross-bridges with actin filaments, linked to hydrolysis of ATP that provides the required energy. We show here the relationship between cross-bridge states, force generation, and Pi release during ramp stretches of active mammalian skeletal muscle fibers at 20°C. The results show that force and Pi release respond quickly to the application of stretch: force rises rapidly, whereas the rate of Pi release decreases abruptly and remains low for the duration of the stretch. These measurements show that biochemical change on the millisecond timescale accompanies the mechanical and structural responses in active muscle fibers. A cross-bridge model is used to simulate the effect of stretch on the distribution of actomyosin cross-bridges, force, and Pi release, with explicit inclusion of ATP, ADP, and Pi in the biochemical states and length-dependence of transitions. In the simulation, stretch causes rapid detachment and reattachment of cross-bridges without release of Pi or ATP hydrolysis.

Introduction

Stretch of active muscle has revealed many aspects of the contractile process. In asynchronous insect flight muscle, it produces a delayed force production that drives ultrahigh frequency wing beats (1). In vertebrate muscle, rapid, small stretches have been used to investigate the properties of attached cross-bridges (2, 3). Stretch over distances longer than the range of the cross bridge provides insights into the normal function of muscle in vivo acting as a brake or acting to stabilize the body. The active muscle responds to such large stretches by producing high force-resisting stretch; the amount of force is greater than isometric force and depends on the velocity of stretch (4, 5, 6, 7, 8). The fact that the force is produced during stretch over long distances is important because it means that cross bridges break and reattach. When active muscle is stretched, it absorbs energy because work is done on the muscle. Some of the absorbed energy is converted to heat, but a significant amount can be stored temporarily in the muscle (9). The site of storage remains elusive, though it is clearly not resynthesis of ATP (10). Instead, ATP use is low during stretch despite the high force (11).

Here we have observed the time-course of ATP use on a fast timescale during stretch itself that has not been done previously, to our knowledge. Fast time-resolution of inorganic phosphate (Pi) produced during stretch of activated permeabilized mammalian muscle fibers is achieved by using a fluorescent reporter of the inorganic phosphate (12, 13).

The results show that the rate of ATP use is reduced almost immediately from the start of the stretch. We have simulated the time-course of the force and Pi release during stretch using a branched cross-bridge model based on that of Lombardi and Piazzesi (14) and Piazzesi et al. (15). We have extended their model by explicitly including Pi, ADP, and ATP. Key features of the model: it is a branched pathway, and one of the branches allows cross-bridges that break during stretch to reattach rapidly without release of Pi.

In the simulation, stretch increases the average strain of attached cross-bridges, causes a small decrease in the number of attached cross-bridges, and decreases the fraction of attached cross-bridges containing ADP and no Pi.

Methods

Fiber preparation from rabbit psoas muscle and the experimental apparatus were described previously (16, 17). A fiber bundle consisting of 1–3 fibers isolated from rabbit psoas muscle was glycerinated and permeabilized with Triton-X100 before crimping and gluing to T-clips with shellac and mounting onto stainless steel-wire hooks. The fiber bundle was held at 20°C. The rotating stage contained six troughs allowing rapid change of the bathing solution. One hook was connected to a force transducer and the other to a servomotor. After a fiber bundle was mounted, its sarcomere length was set to 2.4 μm as determined from the position of the first-order peak of the bundle's laser light diffraction pattern. The bundle diameter was measured at several places along its length. Bundle cross-sectional area was calculated assuming the shape was circular. The clip-to-clip distance was measured and designated as L₀.

The fiber bundle was then put through the following sequence of solution changes:1), rigor solution containing no ATP and no free Ca²⁺; 2), rigor solution containing 32 μM free Ca²⁺; and 3), a solution containing 5 mM NPE-caged ATP (caged ATP) and 1.2 mM MDCC-PBP (the Pi-biosensor) and Ca²⁺. A compound microscope equipped with a 40×, NA 0.75 water immersion objective and modified to fit a photomultiplier tube was used to measure epi-fluorescence from the Pi-biosensor. Contraction was initiated from the rigor state by photolytic release of 1.5 mM ATP from 5 mM NPE-caged ATP triggered by a frequency-doubled ruby laser pulse (16). Two-hundred milliseconds after the photolytic release of ATP and initiation of force development, the fiber bundle was subjected to length changes. All 36 fibers were subjected to constant velocity stretch, and hold; in 17 of these experiments, the hold was followed by constant velocity shortening (Fig. 1 a). The length changes imposed by the motor were 5% L₀ and complete in 0.1 s. Data (force, motor position, fluorescence) were acquired at 0.1-ms intervals.

Figure 1.

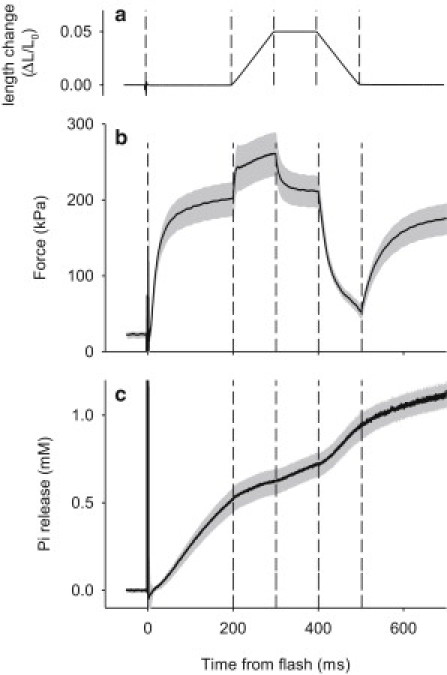
Illustration of the experimental protocol. (a) Length change. (b) Force. (c) Pi release. Panels b and c show mean (line) ±1 (mean ± SE) (shading) for 17 observation on 17 fiber preparations. (Dashed vertical lines) Marking time of: laser flash, the start of stretch, end of stretch, start of shortening, and end of shortening.

Sarcomere length was not recorded during the contractions. It is calculated from force, initial sarcomere length (2.40 μm), and a value for the end compliance of permeabilized rabbit fibers measured in previous studies in the laboratory (17, 18, 19, 20). The mean value of these end compliance measurements was 3.44% L₀/P_o, where P_o is the isometric force (n = 7 fibers). Thus in the experiments reported here the actual sarcomere length was calculated to be 2.32 μm when isometric force had been produced, and 2.41 μm at the end of stretch. The sarcomeres increased in length by 3.9% during the imposed stretch and the velocity of stretch was 39% s⁻¹.

The fluorescence signal was converted to Pi concentration and corrected for Pi-biosensor saturation (21). The concentration of PBP added to the fiber bundles, Y, and the fluorescence signal at each time point, ΔFl, were used to calculate the concentration of Pi bound to PBP, PBP.Pi, as

$$\text{PBP}.\text{Pi}=\text{Y}\times \frac{\Delta Fl}{max\Delta Fl},$$ (1)

where maxΔFl is the maximum fluorescence signal recorded in the experiment.

We measured the apparent dissociation (appK_d) constant of PBP.Pi within fibers, so that Pi produced from ATP hydrolysis, but not bound to PBP, could be evaluated:

$$\text{PBP}.\text{Pi}\leftrightarrow \text{PBP}+\text{Pi}.$$

The appK_d was found by measuring the fluorescence from fibers in solutions containing a known amount of PBP (1.2 or 2.58 mM) and different amounts of added Pi (0–4 mM). Fibers were prepared as described above and rigor induced with Ca²⁺-free rigor solution. The fiber was equilibrated for 10 min in each Pi-containing solution before being transferred to silicone oil and the fluorescence measured.

Results from four such experiments, each with a different fiber and PBP sample, are shown in Fig. 2 a. The line shows the binding curve calculated from the best fit value of appK_d, 15.8 μM. Fitting was done with Excel Solver (http://www.solver.com/) using the observations within abscissa range 0.41 and 1.34 where the curvature of the binding curve is greatest and appK_d affects the fit most strongly. The residuals are shown in Fig. 2 b.

Figure 2.

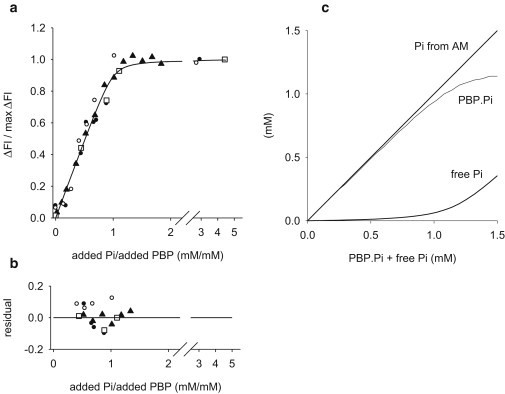
Fluorescence signal and Pi release from actomyosin. (a) Binding curve from control experiments (see text) showing the relationship between fluorescence change (expressed relative to maximum fluorescence change) and the amount of Pi added to a solution containing a known amount of the biosensor, PBP (added Pi expressed relative to amount of PBP). The different symbols are results from independent runs using different PBP samples. The line shows the binding curve calculated with an apparent dissociation constant (appK_d) 15.8 μM, found by fitting to values in abscissa range 0.41–1.34 where the curvature is greatest and where appK_d affects the fit strongly. (b) Shows the residual difference between the each experimental point in panel a used for fitting and the corresponding value from the fitted line. (c) Illustrates the relationship between PBP.Pi, free Pi, and total Pi (= PBP.Pi + free Pi) that was used for experiments on contracting fibers. The PBP.Pi value is derived directly from the biosensor fluorescence signal. Total Pi (PBP.Pi + free Pi = the amount of Pi released due to ATP hydrolysis by actomyosin) is evaluated from PBP.Pi, the amount of PBP added to the fiber (1.2 mM), and the binding curve in panel a. Free Pi is the difference: total Pi – PBP.Pi.

Fig. 2c shows the relationship between total Pi (the amount bound to PBP and the free Pi, calculated from measured appK_d) and the concentration of PBP used here (1.2 mM).

In the experiments on contracting fibers, the amount of Pi released due to ATP hydrolysis by actomyosin is the sum of PBP.Pi and free Pi (see Fig. 2 c). We use the term “Pi release” to mean the total amount of Pi released from the fiber due to ATP hydrolysis by actomyosin. As can be seen in Fig. 2 c, for the condition used in the fiber experiments here with 1.2 mM added PBP, free Pi remains low (<0.1 mM) until >80% of the PBP (1.0 mM) has Pi bound to it.

Phosphocreatine and creatine kinase, which act to maintain a steady ATP concentration, were not used because it is more difficult to maintain the Pi-biosensor free of Pi before photolytic release of ATP when they are present. Each bundle was used once only, to limit the effect of damage by the laser pulse.

Mean values of experimental observations on different fibers are reported. Unless otherwise stated, ± values are standard errors.

Modeling

Modeling was achieved using MATLAB Simulink (The MathWorks, Natick, MA) running on Windows OS personal computers.

Results

Experiments were carried out to measure the time-course of Pi release during stretch of an active muscle fiber preparation at 20°C. Fig. 1 illustrates the protocol and the results for the 17 fiber preparations used in this protocol. Photolytic release of ATP at time zero initiates a rapid rise in force to a value of 203 ± 23 kN.m⁻² (n = 17) during a 200-ms period at constant length (isometric). During this time the fluorescence signal increases; Fig. 1 c shows the Pi release due to hydrolysis of ATP during the cross-bridge cycle derived from the fluorescence signal as described in the Methods. During the isometric period the average rate of Pi release is 2.68 ± 0.28 mM s⁻¹ (n = 17), which corresponds to each myosin molecule releasing Pi at a rate of 34.8 ± 3.7 s⁻¹, assuming a myosin concentration of 0.077 mM. Starting at 200 ms after activation, the fiber preparation is stretched by 5% of its initial length at a constant speed for 100 ms (Fig. 1 a). During the initial part of the stretch the force rises rapidly, and then rises slowly for the duration of the stretch, reaching 260 ± 29 kN.m⁻². The rate of phosphate release decreases sharply at the beginning of the stretch. The average rate is 1.04 ± 0.35 mM.s⁻¹ during the stretch, which is equivalent to 13.5 ± 0.45 s⁻¹ by each myosin molecule (two heads).

The rate of Pi release appears to slow down somewhat during the stretch. In the last 20 ms of the stretch, the rate is 0.34 ± 0.64 mM.s⁻¹, or 4.4 ± 8.3 s⁻¹ by each myosin molecule. At the end of the stretch the fiber preparation was held at constant length for 100 ms during which force decreases to 210 ± 21 kN.m⁻², somewhat higher than the prestretch isometric force level. During this period, the Pi release rate accelerates somewhat to 1.02 ± 0.17 mM.s⁻¹, which is equivalent to 13.2 ± 2.2 s⁻¹ by each myosin molecule. The fiber preparation is then returned to its initial length by applying a 100-ms shortening ramp of the same amplitude and speed as the stretch. By the end of shortening, the force has dropped to 53 ± 9 kN.m⁻², whereas the Pi release rate has increased to 2.06 ± 0.61 mM.s⁻¹, which is equivalent to 26.7 ± 8.0 s⁻¹ by each myosin molecule. The increase in the rate of Pi release is due to the muscle performing work during the shortening phase. At the end of the shortening, there is an isometric period during which the force rises and Pi release continues. Both the force and the rate of Pi release attained during this isometric period are less than in the initial isometric period.

The complete protocol provides evidence about the ability of the Pi-biosensor to continuously measure the rate of Pi release during the contraction with length perturbations and return to the isometric state. The rapid Pi release during fiber shortening shows that the decrease in Pi release rate during the stretch is not attributable to loss of sensitivity of the Pi-biosensor. The protocol also demonstrates that the application of a stretch does not abolish the ability of a fiber to shorten during a subsequent release.

During the 700-ms contraction protocol, the ATP concentration gradually falls from 1.5 mM, which is initially released from caged-ATP, and free ADP accumulates to 1.12 mM matching the release of Pi. Most of the Pi is bound to PBP because the Pi-biosensor binds Pi with high affinity, thus the free Pi concentration reaches only 0.11 mM (see Fig. 2 c). The fact that the rate of Pi release during the final isometric phase is less than that initial isometric phase is likely due to the relatively low ATP and high ADP concentrations late in the protocol. The small increase in free Pi concentration is unlikely to have much effect; in intact muscle cells even when fully rested, Pi is usually in the millimolar range.

We now focus on the speed with which the rate of Pi release changes at the start of the stretch. Fig. 3 shows the time-course of 1), force enhancement and 2), Pi release averaged for 36 muscle fiber preparations for an isometric period followed by the period of stretch. Pi release is slower during stretch than in the isometric period. The slowing of Pi release is more clearly shown by the time-course of the rate of Pi release in Fig. 3 c (noisy trace), which is the derivative of the Pi trace in Fig. 3 b. It is striking here that the rate decreases to less than half within 5–10 ms of the start of stretch.

Figure 3.

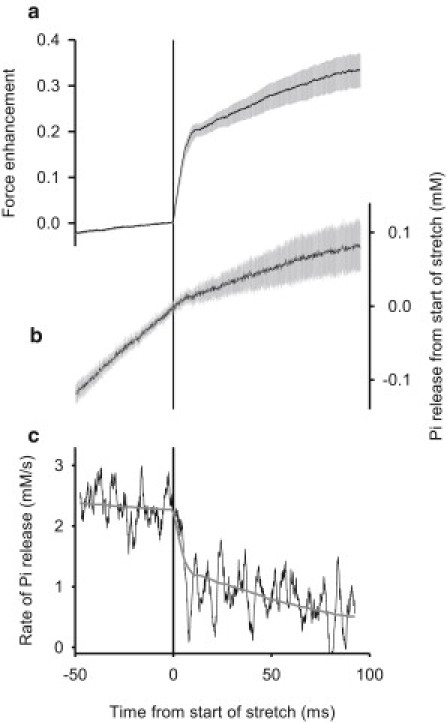
Force and Pi release. (a) Force enhancement. (b) Pi release. (c) Rate of Pi release before and during stretch. Time zero corresponds to the end of the isometric period and the start of constant velocity stretch. Force enhancement = (force at time t – force at time 0)/force at time 0. Mean results from 36 observations on 36 fiber preparations. Each experiment's contribution to the mean was weighted by a factor equal to the inverse of the residual variance of Pi release from the regression mean ± weighed SE = sample standard deviation/sqrt b, where b = (Σweighting factor) ²/Σ (weighting factor²). (c, noisy line) Rate of Pi release obtained by differentiating the relationship shown in b using a second-order Savitzky-Golay filter (34) with a window of 51 points (0.1-ms intervals). (Smooth line) Force enhancement record a multiplied by the slope of the regression line in Fig. 4 + the intercept of that line.

Fig. 4 makes a direct comparison of Pi release rate and force enhancement, where the solid line shows the regression. From this, it is clear that there is a close association between the Pi release rate and force enhancement induced by stretch. This is also illustrated in Fig. 3 c where the observed Pi release rate (noisy line) is shown along with rate of Pi release predicted (smooth line) from the observed force enhancement (Fig. 3 a) and the regression characteristics shown in Fig. 4. The predicted and observed Pi releases rate match well, showing that the association between force and Pi release rate applies at all the time points. In summary, the change in Pi release rate during stretch is like the force, in that both show an early rapid change followed by a slower rate of change.

Figure 4.

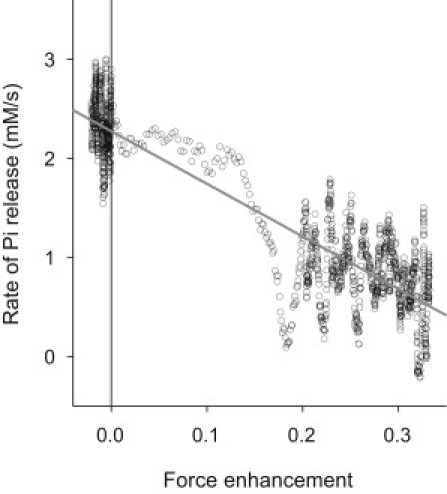
Relation between force enhancement and rate of Pi release. Points are the data (average for 36 fiber preparations) at 0.1-ms intervals for the period from 47 ms before to 92 ms after the start of stretch. (Solid line) The regression line for all points. Slope = −5.31 mM/s per unit of force enhancement, intercept = 2.27 mM/s.

Modeling

We have simulated the time-course of both force and Pi release using a modified version of the Lombardi and Piazzesi model of the cross-bridge during stretch (14, 15). See also Huxley and Simmons (2) and Hill (22) for the antecedents of this model. The reaction scheme of the model is shown in Fig. 5 a and includes eight reactions and six myosin cross-bridge states. Each state in the model is regarded as representing a whole myosin molecule (two heads) and we have assumed that only one myosin head can be attached to actin at any one time. In four of the states (A states), one of the two cross-bridge heads of the myosin is attached to actin, and in the other two states (D states) the myosin is detached from actin. The ligands (ADP and Pi) bound to each of the cross-bridge states are shown. The model also describes the concentrations of free ATP, ADP, and Pi and includes the biosensor PBP and its interaction with Pi.

Figure 5.

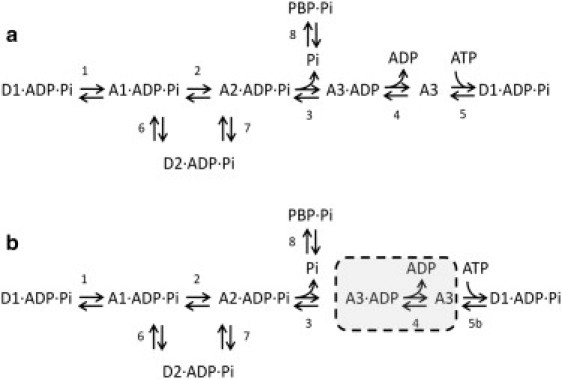
Reaction schemes used for the modeling. D = myosin with both heads detached from actin, A = myosin with one head attached to actin. D1, D2, A1, etc., correspond to states with different bound ligands (ADP, Pi) and different free energy levels. PBP is the fluorescent biosensor, MDCC-PBP. Reactions are identified by numbers, 1–8. (a) Full reaction scheme. (b) Simplified scheme in which A3.ADP and A3 are always in rapid equilibrium and the equilibrium mixture is treated as a single state.

The aim of the modeling is to discover whether a model of the type introduced by Lombardi and Piazzesi and their colleagues (14, 15) can simulate the very rapid changes in force and rate of Pi release that occur at the onset of a period of stretch. Force is produced by the attached states (A1, etc.) and Pi is released by reaction 3. In reaction 4, ADP is released and in reaction 5, ATP is bound and hydrolyzed. The key feature of the reaction scheme is that reactions 6 and 7 occur with the ligands, ADP and Pi, remaining in place, bound to the cross-bridge. This provides a route by which cross-bridges can attach and detach without splitting ATP or releasing Pi.

Force and free energy of cross-bridge states

Fig. 6 shows the free energy of each cross-bridge state as a function of the relative position (x) of myosin and the attachment site on actin. The free energy values of the detached states, D1 and D2, are independent of x. The free energy of the D1 state before and after an ATPase cycle (GD1 and GD1^∗) are shown by the dashed horizontal lines. The GD1^∗ value is the arbitrary zero from which we measure the free energy of all the other states. The value assigned to GD1 is 90 zJ, which is the free energy change for splitting one molecule of ATP and is equivalent to the net free energy change for one complete cycle of the reactions shown. The value of GD2 is an adjustable parameter in the model and the best-fit value (74 zJ) is shown.

Figure 6.

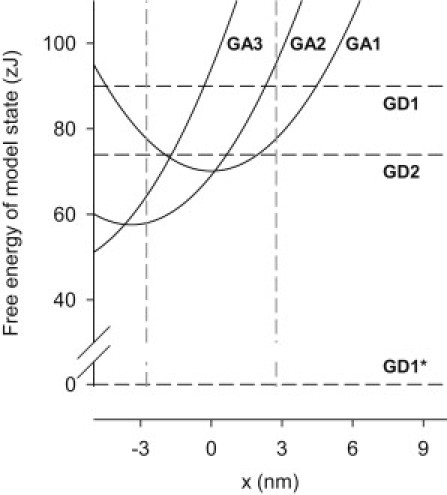
Free energy (G) of the cross-bridge states as a function of x. (Curved lines) Attached states: A1, A2, and A3. (Horizontal lines) Detached states: D1 (before a cycle), D1^∗ (before next cycle), and D2. (Two vertical dashed lines) Boundaries of the permitted region within which cross bridges can form attachments (see text). The label x is filament sliding relative to the point at which isometric force produced by the A1 state is zero. Free energy units: zJ per molecule.

Each of the attached cross-bridges produces a force (f) that depends on its state and is a linear function of x. All attached cross-bridges have the same stiffness (S = df/dx = 2.0 pN/nm). The values of x at which force is zero for the states A1, A2, and A3 are, respectively, 0.0, −3.4, and −6.8 nm. The shapes of the free energy curves for the attached states are all the same. For the three A states,

$$\begin{array}{l}\text{GA}1=0.5\mathit{S}{\left(\mathit{x}\right)}^2+Q1,\\ \text{GA}2=0.5\mathit{S}{\left(\mathit{x}+3.4\right)}^2+Q2,\\ \text{GA}3=0.5\mathit{S}{\left(\mathit{x}+6.8\right)}^2+Q3,\end{array}$$

where Q1, Q2, and Q3 are the minimum free energy values of the three states. Q1 and Q2 are set at 70.1 and 57.6 zJ. Q3 (unlike Q1 and Q2) is adjusted in the fitting of the model; the optimum value was found to be 47.9 zJ (for a standard [Pi] of 1 mM) and the corresponding free energy curve for A3 is shown in the figure.

Rate constants

All reactions are modeled as reversible (reaction 5 has a reverse rate that is negligible). The free energy change for each reaction (ΔG) and thus the equilibrium constant, which is the ratio of the forward and reverse rate constants, for each reaction at each x is specified by the free energy curves shown in Fig. 6. For each reaction and x value, one rate constant of each pair (forward or reverse) is assigned a value, as shown in Table 1 and Fig. 7, and the other is calculated from it and the free energy change.

Table 1.

Rate constants for the model reactions

Rate constant	Equation for rate constant values in s−1	x Range values in nm
F1	= 111	−2.75 ≤ x ≤2.75
	= 0	2.75 < x
R1	= F1/exp (−ΔG1/ b·θ)	−2.75 ≤ x ≤12
F2	= R2 · exp (−ΔG2/ b·θ)	−2.75 ≤ x ≤12
R2	= 1000	−2.75 ≤ x ≤12
F3	= R3 · exp (−ΔG3/ b·θ)	−2.75 ≤ x ≤12
R3	= 1000 · [Pi] / 0.077	−2.75 ≤ x ≤12
F5b	= 1372 · [ATP]/[ADP]	−2.75 ≤ x ≤12
R5b	= F5/exp (−ΔG5/ b·θ)	−2.75 ≤ x ≤ 12
F6	= R6 · exp (−ΔG6/ b·θ)	−2.75 ≤ x ≤ 2.75
	= 436	2.75 < x
R6	= 185	−2.75 ≤ x ≤ 2.75
	= F6/exp (−ΔG6/b·θ)	2.75 < x
F7	= 0	x < 0.016
	= 74.6 · x – 1.2	0.016 ≤ x
R7	= F7/exp (−ΔG7/b·θ)	−2.75 ≤ x ≤12

b Boltzmann's constant; and θ, temperature in degrees Kelvin. F1, F2, etc., are the forward rate constants, and R1, R2, etc., the reverse rate constants, for the numbered reactions in Fig. 5b. The formulas for the free energy changes (ΔG) are: ΔG1 = GA1 – GD1; ΔG2 = GA2 – GA1; ΔG3 = GA3 – GA2; ΔG5 = GD1^∗ – GA3; ΔG6 = GD2 – GA1; and ΔG7 = GD2 – GA2. Reaction 8 remains in equilibrium with appK_d = 15.8 μM.

Figure 7.

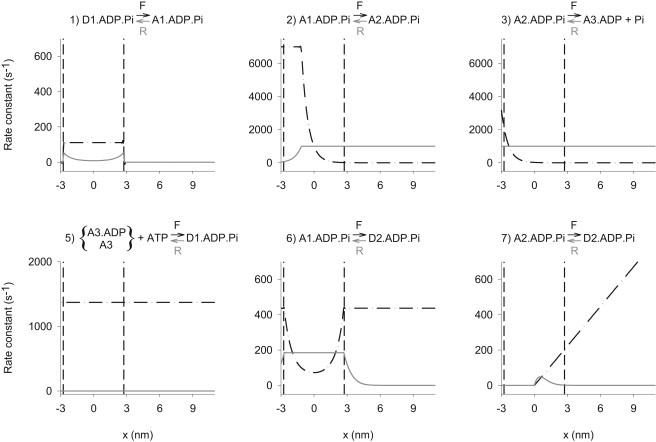
Rate constants for the model reactions as a function of x. Forward rate constants (dashed). Reverse rates (solid). Note that the process of attachment from D1 is a forward reaction, but that attachment from D2 is the reverse of reactions 6 and 7. (Two vertical dashed lines in each graph) Boundaries of the permitted region within which cross-bridges can form attachments. Note that although reactions 6 and 7 have nonzero reverse rate constants, the rates are zero for x > 2.75 nm because the concentration of D2 is zero at x > 2.75 nm. The label x is filament sliding relative to the point at which isometric force produced by the A1 state is zero.

Actin sites are spaced 5.5 nm apart on the thin filaments. Therefore, all cross-bridges are within ±2.75 nm of their nearest actin attachment site. In the model, cross-bridges are considered to interact only with their nearest actin, which is represented by only permitting attachment to actin (reactions 1, 6, and 7) between x = −2.75 and +2.75 nm (broken vertical lines in Figure 6, Figure 7). When a cross-bridge breaks outside this permitted region, its x value returns immediately to a value within the permitted region. The return is attained by subtracting 5.5 nm (or 11 nm or 16.5 nm as needed (14)), and represents the continuation of the rule that any further attachments will be with the nearest actin. The new attachment may be to a different actin than the one from which the myosin has just detached.

When fitting the experimental data with the model in Fig. 5 a it was found that the individual values assigned to F4, R4, and F5 made little difference to the result, as long as the value of F5·F4/R4 was kept constant. It was thus not possible to obtain optimal values for each of these three rate constants individually. It was also found that, under conditions that gave good simulations of the experimental data, the occupancy of the A3 state was always very small (<1% of that of A3.ADP state). We therefore continued the modeling using the reaction scheme in Fig. 5 b where a single state replaces states A3.ADP and A3. The forward rate constant from this state, F5b, is proportion to the ratio [ATP]/[ADP]. See Table 1.

The seven adjustable parameters for the optimization were: GD2, Q3, F1, F5b, R6, and the slope and intercept of the relation between F7 and x. The values for F2 and F3 were kept fixed at the same values as those used by Lombardi and Piazzesi (14) and Piazzesi et al. (15).

Best fit

The results of the optimized simulation of the time-course of force enhancement and Pi release during 50 ms of isometric contraction followed by 80 ms of stretch are shown in Fig. 8, a and b, respectively. The best fit to the data was obtained with the values of rate constants shown in Fig. 7, where their dependence on x is plotted. The fitting used experimental data only for the period from 40 ms before stretch to 40 ms after start of stretch. The simulation is a very good match to both the size and time-course of the observations (Fig. 8) within the period for which it was fitted. Most noteworthy, the model accurately simulates the rapid decrease in rate of Pi release at the start of stretch, which we consider to be the novel feature of the experimental results reported here. The simulation does not match the time course of force beyond 40 ms after the start of stretch. We discuss below some possible reasons for the inability of this model to simulate the slow continuing rise of force.

Figure 8.

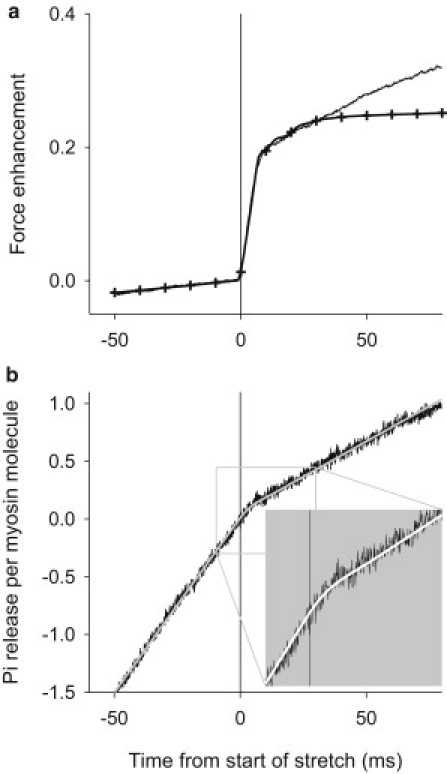
Data compared to simulations. (a) Mean force results from Fig. 1 (solid line) and the simulation from the model (solid line with ticks). (b) Mean Pi release results from Fig. 1 (solid lines) and the simulation from the model (light-shaded line). (Inset) Magnifies the scales by two. Pi release is expressed relative to the myosin concentration. Time zero corresponds to the start of constant velocity stretch that continues for the period shown.

Fig. 9 compares the x-distribution of attached states (a) under isometric conditions and (b) after 50 ms of stretch. Stretch considerably broadens the x-distribution and consequently there is more force produced by each of the attached states, particularly the A1 state. Figure 9, Figure 10 show that the onset of stretch halves the concentration of A3, the only Pi-free state in the reaction scheme. A3 remains low throughout the stretch period. The decrease in A3 contributes to the reduction in flux through the reaction scheme caused by stretch and to the accompanying decrease in the rate of Pi release observed here.

Figure 9.

x-distribution of attached states during isometric and stretch phases of the simulated contraction. (a) Isometric phase just before stretch. (b) During stretch at 0.050 s after the start of stretch. (Two vertical dashed lines) Boundaries of the permitted region within which cross bridges can form attachments. The label x is filament sliding relative to the point at which isometric force produced by A1 is zero.

Figure 10.

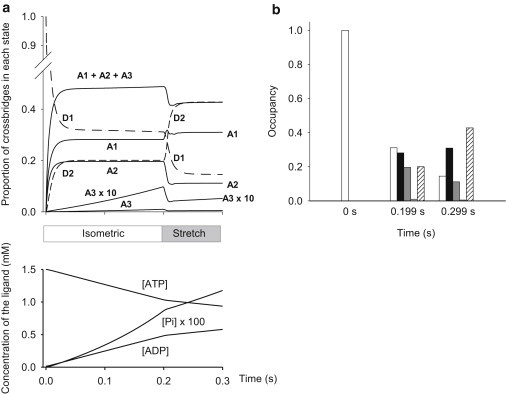
Occupancy of the states during a simulated contraction with stretch. (a) Results of the simulation of the contraction: isometric from 0 to 0.2 s, then stretch until 0.3 s. (Upper graph) Time course of the occupancy of each state as a proportion of the total cross-bridge population. (Lower graph) Corresponding concentrations of ligands, ATP, ADP, and Pi. Note that these are free concentrations and that the values for Pi have been multiplied by 100 for visibility. (b) The figure picks three time-points in panel a, namely before contraction (t = 0 s), at the end of the isometric period (t = 0.199 s), and during stretch (t = 0.299 s) to show how state occupancy differs. Open bars: D1; black bars: A1; dark gray bars: A2; light gray bars: A3; hatched bars: D2.

Discussion

The experiments described above demonstrate that application of a ramp stretch in permeabilized muscle fibers during contraction rapidly decreases the rate of Pi release. The values for force generation and for the rate of Pi release during the isometric period before the stretch in permeabilized psoas fibers at 20°C measured here are similar to values reported previously using the same methods (13, 17).

Stretch causes a sharp decrease in the rate of Pi release at the beginning of the stretch, to one-third of its value during the isometric phase. The decrease in the Pi release lasts for the duration of the ramp stretch. The force response to a ramp stretch causes a biphasic response: an initial rapid rise in force followed by a slower increase to a level 30% higher than the isometric force. The rapid rise in force lasts 10–20 ms at the beginning of the stretch, which corresponds to a stretch amplitude of 6–12 nm per half sarcomere. This distance corresponds to the elastic reach of attached cross-bridges, indicating that in the first 20 ms, all of the attached cross-bridges are forcibly detached by the ramp stretch. After this phase of cross-bridge detachment, force is maintained at a high level ∼30% above the isometric level. This force enhancement by stretch is similar to that reported for human permeabilized 2A/2X fibers (23). In most experiments with intact fibers, the force enhancement is greater (for example: rat (7) and frog (6, 9, 14)).

Stretch and the cross-bridge cycle

Some features of cross-bridge function during stretch are clear from qualitative inspection of our experimental results even without detailed modeling. Our results agree with numerous earlier studies (4, 5, 6, 7, 14) in showing that, during stretch, force is maintained higher than the isometric value over a range of filament sliding distances, which is much larger than the reach of an attached cross-bridge. Thus, bridges detached during stretch must reattach again as the stretch continues. Also in agreement with earlier studies (9, 11, 24) we find that the average rate of Pi release during stretch is much lower than during isometric contraction. Our results extend earlier work by showing that the change in the rate of Pi release occurs very quickly after the beginning of the stretch: the change in Pi release occurs as quickly as the change in force. This temporal association suggests a mechanistic link between force generation and biochemical change at the ATPase site, for example that distortion of the active site modifies the ability of inorganic phosphate to escape. This structural link, which requires further study, shows biochemical and structural coupling at this stage in the cycle, and illustrates a millisecond-scale mechanism to adapt cells to their changing environment.

The low rate of Pi release during stretch means that cross-bridge reattachment, which as indicated above must be happening continuously during stretch, is not via the steps that occur during isometric contraction or shortening, where ATP hydrolysis by myosin precedes each cross-bridge attachment. Thus to account for the full range of contractile functions, including stretch, the cross-bridge cycle must include a detachment and reattachment that does not involve ATP hydrolysis, in addition to the conventional cycle that occurs under isometric conditions and during shortening. In other words, an unbranched cross-bridge cycle that consists of only sequential steps through attached and detached states, without any branches to a separate detached state, cannot account for the energetics and mechanics of stretch.

The models by Huxley (25), Lymn and Taylor (26), and Huxley and Simmons (2) are examples that consist of such unbranched cycles, although some of these authors, for example, Huxley (25), were clearly aware of the limitations of unbranched models. It is also worth noting that the mechanics and energetics of stretch cannot be explained by reversal of the unbranched cycle that operates during isometric contraction and shortening, because such reversal would synthesize ATP, a phenomenon for which there is no experimental evidence despite extensive searches (review by Loiselle et al. (10)).

Kinetic model

We have used a modified version of the cross-bridge model that was developed by Lombardi and Piazzesi (14) to account for the time-course of force production during stretch. The key modification we have introduced is assignment of Pi release from the cross-bridge to reaction 3, which is the transition from the A2 to A3 state. Thus we can include our measurements of the time-course of Pi release as a constraint along with the time-course of force when fitting the characteristics of the model.

The additional force produced during stretch, 30% above isometric force, could indicate either a 30% increase in the fraction of attached cross bridges, or that attached cross bridges exert 30% more force during stretching. Our model accounts for the extra force entirely by the cross-bridges being more strained during stretch and thus producing more force than isometric (Fig. 9), rather than by an increase in the proportion of attached bridges. Indeed, the proportion attached actually falls during the stretch (Fig. 10). The slow rise in force, which follows the 10 ms of rapid force increase, is only partly explained by our model. After 30 ms of stretch, the observations and the model clearly diverge (Fig. 8 a), suggesting that the continuing rise in force is due to factors not included in our model. This slow phase of the force rise during stretch has previously been attributed to stretch of titin (7, 27, 28). Another possible mechanism that could contribute to the slow rise of force is the development of nonuniform velocity of stretch along the length of the fiber (29).

A simpler model of this type, lacking a D2 state, has been used by Getz et al. (8) to successfully simulate the force response to stretch in rabbit muscle fibers at 10°C. However, we have not been able to make good simulations of our experimental results (20°C) for both Pi release and force with a model lacking the D2 state. It seems possible that different models are required for these two temperatures. Getz et al. (8) results show that the force increase during stretch at 10°C is much greater than the increase we got at 20°C. Various factors that depress isometric force have either less or no effect on force during stretch (30, 31, 32, 33). Therefore, cooling may depress isometric force much more than it depresses force during stretch. However, their conclusion about the mechanism of the force response to stretch is similar to ours; in both cases, extra force is produced by bridges that have not released phosphate, being extended to larger x values.

It has been observed in frog muscle (3) that the stiffness of the cross-bridge array increases very quickly at the start of stretch. This increase in stiffness has been attributed to the attachment of the second myosin head to actin. Clearly our model does not predict a rise in stiffness during stretch and we have no evidence about stiffness. Measurements of stiffness, force changes, and Pi release during stretch would provide a powerful data set for refinement of the model we have used here.

A notable difference between the results reported here for permeabilized fibers from rabbit and results from intact frog fibers modeled by Lombardi and Piazzesi (14) is the amount of force enhancement caused by stretch; there is much less force enhancement by permeabilized rabbit fibers than intact frog fibers (14). A model consisting of the same cross-bridge states (Fig. 5) has proved able to account for both sets of data, so the same reaction pathway could operate in both the permeabilized rabbit fibers and intact frog fibers.

Two major differences in the rate constants can be identified that allow the reaction scheme to accommodate both sets of results:

First, the forward rate constants for reactions 6 and 7 (detachment into the D2 state) are much greater for permeabilized rabbit fibers (Table 1) than intact frog fibers (14). This difference is particularly marked in the x region between 3 and 9 nm (reactions 6 and 7 in Fig. 7). Thus, in the permeabilized rabbit version of the model, a small degree of stretch considerably increases the rates of reactions 6 and 7 detaching bridges into the D2 state before the force they bear has increased much. In contrast, the corresponding detachments in intact frog fibers occur less rapidly and thus occur at higher x values, where the cross-bridges are exerting more force (14).

Second, the reverse rate constant for reaction 6 (reattachment from the D2 state) is much higher in the model for intact frog fibers than in the model for permeabilized rabbit fibers, so once the frog bridges have detached into D2, they more quickly reattach and continue producing force.

Another notable difference is in the occupancy of the D2 state during isometric contraction. In the intact frog fiber version of the model (14) there are no cross bridges in the D2 state during isometric contraction, but ∼20% of the bridges in permeabilized rabbit fibers are in this state (see Fig. 10).

We have not tried to extend our model to explain the force and rate of Pi release during shortening. For this purpose, the model would require a number of extra adjustable parameters. To be able to optimize these parameters rigorously to give meaningful values would require a more complete set of experimental data than is currently available, for example: evidence from a number of different velocities of both stretch and shortening. The use of the model here is intended to test whether a model of the type introduced by Lombardi and Piazzesi (14) can explain the very rapid changes in rate of Pi release that we have shown to occur at the onset of periods of stretch. We conclude that the model is indeed very suitable for this purpose, and possibly capable of expansion to a wider domain.

Editor: Christopher Lewis Berger.