Power of Data Mining Methods to Detect Genetic Associations and Interactions

Abstract

Background

Genetic association studies, thus far, have focused on the analysis of individual main effects of SNP markers. Nonetheless, there is a clear need for modeling epistasis or gene-gene interactions to better understand the biologic basis of existing associations. Tree-based methods have been widely studied as tools for building prediction models based on complex variable interactions. An understanding of the power of such methods for the discovery of genetic associations in the presence of complex interactions is of great importance. Here, we systematically evaluate the power of three leading algorithms: random forests (RF), Monte Carlo logic regression (MCLR), and multifactor dimensionality reduction (MDR).

Methods

We use the algorithm-specific variable importance measures (VIMs) as statistics and employ permutation-based resampling to generate the null distribution and associated p values. The power of the three is assessed via simulation studies. Additionally, in a data analysis, we evaluate the associations between individual SNPs in pro-inflammatory and immunoregulatory genes and the risk of non-Hodgkin lymphoma.

Results

The power of RF is highest in all simulation models, that of MCLR is similar to RF in half, and that of MDR is consistently the lowest.

Conclusions

Our study indicates that the power of RF VIMs is most reliable. However, in addition to tuning parameters, the power of RF is notably influenced by the type of variable (continuous vs. categorical) and the chosen VIM.

1. Introduction

Recently, genome-wide association studies (GWAS) have been tremendously successful in identifying susceptibility loci for a variety of complex traits. Thus far, the primary analyses of these studies have focused solely on main effects of individual SNP markers, in large part due to the computational scalability of the analysis of hundreds of thousands or even millions of genetic markers. It is commonly believed that epistasis or gene-gene interactions play an important role in the pathogenesis of complex diseases, and the current one-marker-at-a-time approach may mask the effect of important genetic loci. However, to date, simple pairwise gene-gene interaction searches in GWAS have failed to identify robust epistasis findings. One possible explanation is that gene-gene interactions, if present, are likely to involve complex networks that are not well modeled by traditional stepwise regression-based methods.

In the statistical and machine learning literature, tree-based regression methods are often advocated for modeling complex associations between an outcome and multiple covariates. The performance of these methods has been widely studied using prediction- or classification-error as the main criterion for optimization. The goal of the current article is to study the potential utility of these methods for genetic association based on a smaller number of candidate SNPs, where the primary goal is often discovery, not prediction. Several other studies have recently employed the tree-based method random forests (RF) [1] for investigating gene-gene and gene-environment interactions, including a critical survey by Cordell [2]. Lunetta et al. [3] show that RF is more efficient than Fisher's exact test for ranking true disease-associated SNPs. García-Magariños et al. [4] compare the top-rated SNP as chosen by RF, classification and regression trees (CART), logistic regression, and multifactor dimensionality reduction (MDR) over numerous settings including several with missing data, whereas Szymczak et al. [5] compare RF and ensemble methods to penalized regression and network analyses. Jiang et al. [6] use RF Gini variable importance measure to rank SNPs before implementing a forward feature selection algorithm to choose a subset of SNPs and then adopt a hierarchical procedure (unrelated to RF) to determine the statistical significance of the subset. Their proposed method is compared to BEAM, logistic regression, and the single locus χ² test. Wang et al. [7] compute a null distribution in the same manner as we describe in the following but focus the comparison of their proposed maximal conditional χ² to a univariate test and the Gini and permutation importance measures. Altmann et al. [8] compute a null distribution and subsequently fit a probability (Gaussian, log-normal or γ) distribution to the null importancesand estimate the distribution parameters via maximum likelihood in order to derive a p value. If none of the three distributions are appropriate, they use a non-parametric estimate of the p values similar to the approach outlined below. They focus on two variable importance measures in simulations and data analysis: RF Gini importance and mutual information (see [9]). Here, we compare the power of the four measures of variable importance offered by the R package randomForest to each other and to the measures provided by Monte Carlo logic regression (MCLR) and MDR. We begin by describing the three algorithms and the procedure for generating SNP-specific p values in Section 2. The simulation scenarios are detailed in Section 3.1 and data analysis in Section 3.2. Conclusions are offered in Section 4.

2. Methods

RF is now one of the most popular tree-based algorithms with applications in many scientific disciplines. Our goal is to assess RF measures of variable importance as statistics for detecting associations. Further, we compare performance of RF to two other leading algorithms, MCLR and MDR, both of which have been applied to genetic epidemiologic studies.

2.1. Algorithms

2.1.1. Random Forests

RF is a bagging (bootstrap aggregating) algorithm used for measuring the predictive ability and importance of a set of variables. RF builds a collection of CART [10] from multiple bootstrap samples of the original data. The number of trees in a forest, nT, is typically 500 or 1,000. For an individual tree, the observations in the bootstrap sample are referred to as the training sample and those observations left out (approximately one third of the total) are called the ‘out-of-bag’ sample. In addition to using bootstrap samples to build numerous trees, RF differs from CART in two important ways. First, RF does not prune, that is, each individual tree is grown to the largest extent possible. This increases the strength of prediction for any individual tree by achieving low bias. Second, for each node within each tree, mtry variables are selected at random from the total p in the original data set and the best split of the mtry variables is used to split the node. By default, mtry is equal to the square root of the number of total variables, i.e. mtry = √p. The purpose of this random variable selection is to decrease the correlation between trees in the forest while maintaining low bias [1]. Both low bias and low correlation contribute to the reduced prediction error of the algorithm.

With a categorical outcome, subsequent to assembling the forest, each observation is classified by the trees for which it was ‘out-of-bag’. A tally of those classifications leads to a final class assignment based on a majority ‘vote’ by the trees, i.e. forest. The prediction error of the forest is then estimated by comparing the predicted class of the out-of-bag observations to their true class.

In classification, the R package randomForest used here (see [11,12]) returns four measures of variable importance: the class-specific measures computed as mean decrease in accuracy for each class (in the two-class scenario, these are labeled out0 and out1); the mean decrease in accuracy over all classes (overall), and the mean decrease in the Gini index (gini)[11]. The first three are calculated as the average increase in prediction error (i.e. decrease in accuracy) when the values of an individual variable are randomly permuted. Giniis based on the measure for splitting a parent node into two daughter nodes. That is, at each split in a tree, one of mtry variables is selected to dichotomize the observations based on the Ginimeasure, thus decreasing the Giniindex value. The corresponding variable importance measure is calculated by summing the decrease in the entire forest due to a given variable and normalizing by the number of trees.

To evaluate RF as well as compare it to the other algorithms, a p value was assessed for each of the four variable importance measures. To do so, an initial, observed, data set was simulated with n_cases and n_controls using one of the three models outlined in Section 3.1. When both evaluating RF and comparing it to MDR, the SNP values were input as continuous variables; however, when in comparison to MCLR, they were converted to dummy variables as described in Section 2.1.2. In either case, the initial data set was used to generate a null distribution by permuting the case/control status labels. The permutation was repeated B = 100,000 times, each time RF was implemented to predict the permuted labels. The four importance measures were recorded for each variable across the B permuted data sets. After the null distribution was generated, the RF algorithm was run on the initial data set with un-permuted status labels, with nT trees and mtry randomly selected variables for each split. Again, for each variable, the four importance measures were recorded. Subsequently, an additional nsim − 1 data sets were simulated from the chosen model and, for each, the RF variable importance measures were recorded. We save computational time by using a single simulated null distribution in all of the different simulation studies. The approach is justified based on the ground that in large samples all the association test statistics are expected to converge to a theoretical null distribution that does not depend on the actual simulation setting.

Subsequently, the values for the real, observed data were compared to that of the null distribution for estimating the p-th p value via the following formula:

$$p\hspace{0.17em}valu{e}_p\hspace{0.17em}=1-\hspace{0.17em}\frac{{\sum }_{b=1}^{B}I\left(V{I}_p^O>\hspace{0.17em}V{I}_p^b\right)}{B},$$ (1)

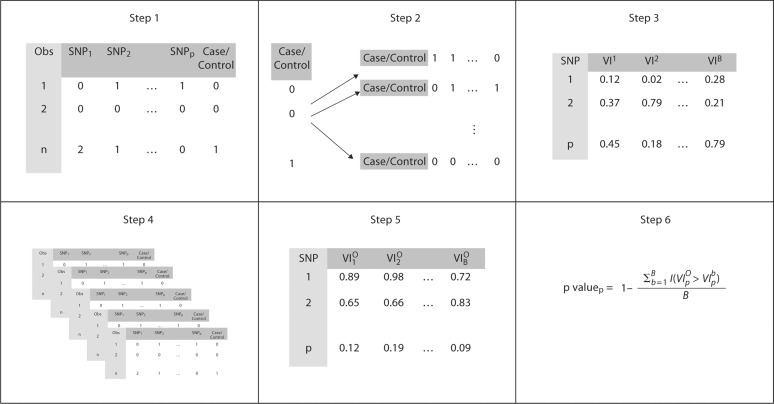
where B is the number of permuted samples, VI_p^O is the variable importance measure for the p-th variable as assessed using the observed (non-permuted) data set, and VI^b_p is the variable importance measure for the p-th variable as assessed using the b = 1, …, B sample with permuted labels (fig. 1).

Fig. 1.

Summary of steps for generation of null distribution and p values. In step 1, an initial data set is generated from the chosen model with n observations (Obs) and p SNPs. In step 2, the case/control status is permuted B times and paired with the original SNPs resulting in B data sets for the null distribution. In step 3, the algorithm is run B times, once for each of the B data sets and the variable importance measure is recorded (VI^b, where b = 1, …, B). In step 4, nsim − 1 additional data sets are generated from the chosen model. In step 5, the algorithm is run on each generated data set (with un-permuted labels) and the VI^O are recorded. In step 6, the p values for the p-th SNP are calculated by summing the number of times VI_p^O is greater than the B, VI_p^b from the null distribution.

As this entire procedure was repeated nsim times, there were nsim p values for each of the variables. The reported value for each variable was the ratio of p values out of nsim that fall below a specified cutoff, e.g. α_cutoff = 0.05/p. For comparisons between RF and MCLR, the reported value for each variable was the sum of its corresponding dummy variables’ p values out of nsim that fall below the specified cutoff. In the simulations presented below, four values for mtry ∈ (1, 3, 5, 7) and two for nT ∈ (500, 1,000) were examined for all models.

2.1.2. Monte Carlo Logic Regression

Logic regression is a regression methodology which forms Boolean combinations of binary covariates [13]. For our goal of assessing a measure of variable importance, we focused on MCLR. This implementation returns a summary of all models built using Monte Carlo methods as opposed to returning a single model as in the original logic regression. In MCLR, the suggested variable importance measure is how frequently an individual variable appears across all models. From the summary, the contribution of each variable can be evaluated by the ratio of the number of times it was included in any of the models divided by the total number of models. MCLR is implemented in the R package LogicReg [14]. Details of the simulation and p value assessment are given in the online supplementary Section 1.1 (for all online suppl. material, see www.karger.com/doi/10.1159/000330579).

2.1.3. Multifactor Dimensionality Reduction

MDR is a non-parametric and genetic model-free algorithm which reduces a high-dimensional data structure to a single dimension for the purpose of finding interactions among small sample sizes [15]. Implementing v-fold cross-validation, MDR attempts to find the best combination of N (user-defined) variables for classification purposes. As implemented in the R package Rmdr [16], a list of the best N variables is returned for each of the v cross-validation iterations.

To assess variable importance, the frequency with which each variable is included in the best combinations within the v-folds can be ascertained. To quantify this over v-folds, we have defined the variable importance measure for MDR as the number of times the p-th variable is chosen in the reported v-fold combinations divided by v, the total number of cross-validation folds performed. Details of the p value assessment are given in the online supplementary Section 1.2.

3. Results

3.1. Synthetic Data

Three different models were used to generate data for the simulations. The first two models (Sections 3.1.1 and 3.1.2) are borrowed from Huang et al. [17]. In both, there are 30 measured loci of which 6 are related to the probability of disease. The other 24 loci are independently and identically distributed, and the genotype is prevalent type or not, with equal probabilities. The first is based on an accumulation of mutations (additive model), while the second requires exact mutations (exact model). In Section 3.1.3, we explore a third model which more realistically portrays current association studies. In this third model, we assume that the genotyped SNPs themselves may not be functional (tagging SNPs). As such, numerous scenarios are generated including different levels of association between the unobserved causal SNPs and the observed tagging SNPs (details given in Section 3.1.3 and online suppl. tables 1, 2, 3). For each simulation model, data sets with 200 and 500 observations were generated.

3.1.1. Additive Model

The first model borrowed from Huang et al. [17] is referred to as ‘additive’ in that the effects of mutations on disease are simply additive based on the number of mutations, M, at the 6 sites (ranging from 0 to 12) surpassing specific thresholds. The probability of disease, D, is written as:

$$P(D|M)\hspace{0.17em}=\hspace{0.17em}0.1I(M\ge \hspace{0.17em}6)\hspace{0.17em}+\hspace{0.17em}0.4I(M\hspace{0.17em}\ge \hspace{0.17em}7)\hspace{0.17em}+\hspace{0.17em}0.1I(M\ge \hspace{0.17em}9),$$

where I(·) is the indicator function. Thus, if the mutations accumulate past the specified thresholds, there will be a high risk of disease, whereas if there are few (here <4) variants, there is minimal risk, i.e. P(D ∣ M) = 0. The number of mutations at the 6 loci, m₁, …, m₆, are independently and identically distributed as:

$$P(m_i\hspace{0.17em}=\hspace{0.17em}j)\hspace{0.17em}=\hspace{0.17em}{(}_j^2)\hspace{0.17em}{0.5}^2,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{where j}=0,\hspace{0.17em}1,\hspace{0.17em}2\hspace{0.17em}\hspace{0.17em}\text{and i}\hspace{0.17em}=\hspace{0.17em}1,\hspace{0.17em}2,\hspace{0.17em}\mathrm{\dots },\hspace{0.17em}6.$$

Thus, M ∼ Binomial(12, 0.5) and the unconditional probability of disease is P(D) = 0.5 because P(D ∣ M) = P(D ∣ 12 – M) and M ∼ 12 – M. The marginal relative risk for the 6 key SNPs is approximately 2.3.

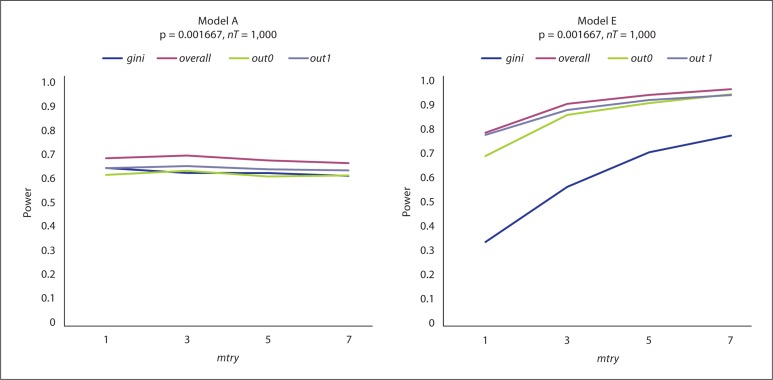
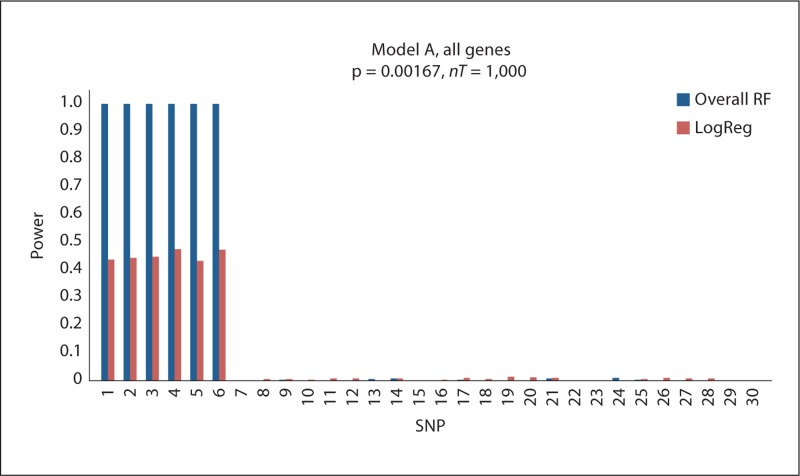
For the additive model (Model A), the power of RF variable importance measures to select the 6 key SNPs is shown on the left of figure 2. The four measures have similar power which all remain consistent as mtry increases. As expected, the power increases (from approximately 0.65 to 1) when the sample size doubles (online suppl. fig. 1). The type I error for these comparisons is displayed in the top left of table 1. For both sample sizes, gini has the smallest error followed by overall and out1. Although, when n = 200, the error for gini decreases (from 0.014 to 0.002), the error for the others remains the same as mtry increases. Figure 3 displays the power of RF and MCLR when dummy variables are used for the SNPs with a sample size of 200. Figure 3 compares the two algorithms for each of the 30 SNPs. The power of the overall measure for RF is approximately 0.97 for all 6 related SNPs (SNPs 1–6) and 0 for the remaining 24 unrelated SNPs. MCLR has a range of 0.43–0.47 for the 6 related SNPs and almost 0 for the remaining unrelated SNPs. The same comparison with 500 observations can be found on the top right side of online supplementary figure 2 where the power for RF increases slightly while that of MCLR noticeably increases to 0.8–0.85. The top left of the same figure shows the power averaged over the 6 effective genes in Model A for each of the RF measures as mtry is increased. As with continuous valued SNPs (shown in fig. 2 and online suppl. fig. 1), the four measures perform consistently over an increasing mtry and similarly to each other. As seen in online supplementary figure 3, the power for MDR ranges from 0.2 to 0.25 for the related SNPs, while the type I error is 0 for the unrelated SNPs.

Fig. 2.

RF results for Model A and Model E simulations. With 200 observations, power is measured on the y-axis and mtry on the x-axis, p value is adjusted for 30 SNPs, and nT = 1,000. The different lines correspond to four RF variable importance measures.

Table 1.

Type I error for RFs

Sample size	mtry	Model A				Model E
		1	3	5	7	1	3	5	7
200	gini	0.014	0.004	0.002	0.002	0.066	0.028	0.022	0.008
	overall	0.028	0.022	0.016	0.032	0.06	0.042	0.038	0.04
	outO	0.038	0.03	0.032	0.032	0.058	0.046	0.038	0.04
	outl	0.036	0.034	0.03	0.03	0.046	0.032	0.032	0.036
500	gini	0.002	0	0	0	0.006	0	0	0
	overall	0.04	0.022	0.03	0.028	0.05	0.038	0.022	0.038
	outO	0.046	0.042	0.04	0.042	0.038	0.016	0.024	0.058
	outl	0.042	0.028	0.026	0.03	0.056	0.044	0.04	0.052

Sample size	mtry	Tagging SNP Model 1				Tagging SNP Model 2
		1	3	5	7	1	3	5	7
200	gini	0.05	0.04	0.028	0.03	0.014	0.012	0.01	0.008
	overall	0.036	0.046	0.038	0.036	0.02	0.016	0.014	0.018
	outO	0.046	0.036	0.04	0.036	0.024	0.026	0.014	0.026
	outl	0.028	0.042	0.04	0.038	0.02	0.008	0.008	0.014
500	gini	0.036	0.038	0.04	0.042	0.048	0.036	0.036	0.03
	overall	0.042	0.032	0.042	0.038	0.026	0.026	0.026	0.038
	outO	0.04	0.038	0.036	0.028	0.026	0.024	0.028	0.034
	outl	0.038	0.028	0.04	0.032	0.036	0.026	0.014	0.024

For all, nT = 1,000, and the columns represent different values of mtry.

Fig. 3.

RF and MCLR results for Model A simulations. Results are based on 200 observations with dummy variables for the SNPs. Power is measured on the y-axis. RF overall is compared to MCLR over each SNP (x-axis). p values are adjusted for 30 SNPs and nT = 1,000.

3.1.2. Exact Model

In the second model from Huang et al. [17], there is an epistatic impact of the number of mutations at the 6 sites on the probability of disease, which is written as:

$$P(D|M)\hspace{0.17em}=\hspace{0.17em}0.1\hspace{0.17em}+\hspace{0.17em}0.8I(M\hspace{0.17em}=\hspace{0.17em}12).$$

Thus, it is not as detrimental to have mutations with the exact model (Model E) as it is with Model A because Model E requires all 12 mutations in order for a high risk of disease, whereas the risk increases with an increasing number of mutations in Model A. Here m₁, …, m₆ are also i.i.d., but with the following distribution:

$$P(m_i\hspace{0.17em}=\hspace{0.17em}j)\hspace{0.17em}=\hspace{0.17em}{(}_j^2){0.9}^j/{0.1}^{2-j},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{where j}\hspace{0.17em}=\hspace{0.17em}0,1,2\hspace{0.17em}\text{and i}\hspace{0.17em}=\hspace{0.17em}1,2,\hspace{0.17em}\mathrm{\dots }\hspace{0.17em}6.$$

Thus, M ∼ Binomial(12, 0.9) and the unconditional probability of disease under this model is P(D) = 0.9¹² 0.9 + (1 − 0.9¹²) 0.1 = 0.326. The marginal relative risk for the 6 key SNPs is approximately 5.5.

For Model E, the power in selecting the first of the 6 related SNPs for RF variable importance measures is shown on the right of figure 2. For 200 observations, three of the measures have similar power which increases as mtry increases. In comparison, gini has a markedly lower power, e.g. 0.3 versus 0.75 for mtry = 1, although it too increases with mtry. Again, the power for all measures increases with the sample size, and any distance between gini and the others becomes indistinguishable (online suppl. fig. 1). The type I error for these comparisons is displayed in the top right of table 1. For both sample sizes, gini has the smallest error, followed by out1 and overall. Although, when n = 200, the error for gini decreases (from 0.066 to 0.008), the error for the others remains similar as mtry increases. The power of RF when dummy variables are used for Model E (shown in online suppl. fig. 2) is identical to that shown in figure 3 for Model A. As with continuous valued SNPs, the four measures perform consistently over an increasing mtry and similar to each other. As illustrated in online supplementary figure 2, for Model E the power of the overall measure for RF as well as that of MCLR is approximately 1.0 for all 6 related SNPs (SNPs 1–6) and 0 for the remaining 24 unrelated SNPs. As seen in online supplementary figure 3, the power for MDR for Model E is slightly higher than for Model A, falling within the range of 0.2–0.3.

3.1.3. Tagging SNPs

The goal of this simulation model is to see how the three different algorithms perform in current association studies where the genotyped SNPs themselves may not be functional. We assume there are 10 candidate genes, denoted by G₁, …, G₁₀, under study, say within a pathway. For each gene i, we assume 6 tagging SNPs, T_i1, …, T_i6, have been genotyped, giving rise to a total of 60 SNPs. We assume two different disease risk models: in the first, Model 1, only G₁ and G₆ contain a causal SNP, denoted S₁ and S₆, and the risk of the disease is given by

$$\text{logit}\hspace{0.17em}\{Pr(D\hspace{0.17em}=\hspace{0.17em}1\hspace{0.17em}|\hspace{0.17em}{S}_1,S_6)\}\hspace{0.17em}=\hspace{0.17em}\alpha \hspace{0.17em}+\hspace{0.17em}\beta G(S_1)\hspace{0.17em}\cdot \hspace{0.17em}G(S_6),$$

where G(S_i) denote a particular genotype coding for the causal SNP S_i. For example, if S_i is coded as dominant, then G(0) = 0, G(1) = 1, and G(2) = 1. The marginal relative risks for the 6 tagging SNPs in G₁ range from 0.89 to 2.25 and in G₆ range from 0.82 to 1.82.

Under the second risk model, Model 2, we assume G₁, G₂, G₆, and G₇ each contain a causal SNP, denoted S₁, S₂, S₆, and S₇, and the risk of the disease is given by

$$\text{logit}\hspace{0.17em}\{Pr(D\hspace{0.17em}=\hspace{0.17em}1\hspace{0.17em}|\hspace{0.17em}{S}_1,S_2,S_6,S_7)\}\hspace{0.17em}=\hspace{0.17em}\alpha \hspace{0.17em}+\hspace{0.17em}{\beta }_{1}G(S_1)\hspace{0.17em}\cdot \hspace{0.17em}G(S_6)\hspace{0.17em}+\hspace{0.17em}{\beta }_{2}G(S_2)\hspace{0.17em}\cdot \hspace{0.17em}G(S_7).$$

The haplotypes and their frequencies defined by the combination of (potential) causal (S_i) and marker SNPs (T_i1, …, T_i6) for the genes G₁, …, G₅ are given in online supplementary table 1. The first position indicates the location of the potential causal SNP. Note that the frequency of the causal SNP is approximately 12%. Similar haplotype frequencies for the genes G₆, …, G₁₀ are given in online supplementary tables 2 and 3 for two different scenarios that correspond to two different frequencies for the causal SNP(s): (F1) 12.7% and (F2) 4%. For each table, we use three different values of δwhich correspond to different levels of R² between the causal SNP and tagging SNPs haplotype. The marginal relative risks for the 6 tagging SNPs in G₁ range from 0.91 to 1.66, in G₂ range from 0.89 to 1.69, in G₆ range from 0.87 to 1.47, and in G₇ range from 0.87 to 1.45.

The data is generated as follows: given the set of haplotype frequencies in online supplementary tables 1–3, first generate the diplotype (haplotype pair) for a given gene assuming Hardy-Weinberg equilibrium. Under Hardy-Weinberg equilibrium, note

$$\text{Pr}(\{h_k,\hspace{0.17em}{h}_l\})\hspace{0.17em}=\hspace{0.17em}{\theta }_k^2\hspace{0.17em}\text{if}k\hspace{0.17em}=\hspace{0.17em}l\hspace{0.17em}=\hspace{0.17em}2{\theta }_k{\theta }_l\hspace{0.17em}\text{if}\hspace{0.17em}k\ne \hspace{0.17em}l,$$

where θ_k denotes the haplotype frequencies given in the tables. Thus, for different subjects, the diplotype data for a given gene, say G_k, can be generated by i.i.d. sampling from a suitable multinomial distribution. Once we have the diplotype status for a subject, the genotype data at a given position (locus) would be given simply by the sum of the 0 − 1 numeric codes (online suppl. tables 1–3) at that locus on the constituent haplotype pair for that subject. Given the genotype data, we generate disease status for a subject assuming the risk model (Model 1 or 2). For each simulation, a case-control sample is generated by first simulating data from a large random sample and then using it as the database for further selecting the pre-specified number of cases and controls. The intercept parameter of the disease risk model is manipulated to make the Pr(D = 1) = 0.01 in the underlying population.

For the analysis of the data using different data mining methods, we assume we have the (unphased) genotype data from the marker SNPs only, and not from the causal SNPs. In other words, we assume that for each gene we have the genotype data on all but the first locus. In total, there are 2 × 2 × 3 = 12 different parameter settings corresponding to two different risk models, two different sets of haplotype frequencies for G₂, …, G₆ (online suppl. tables 1–3) and three different values for δ.

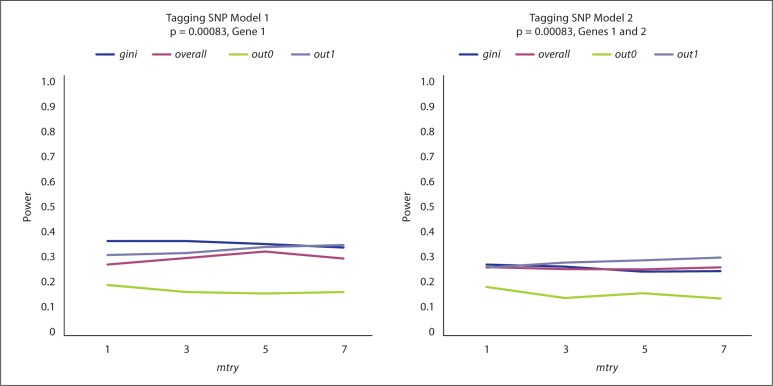
Figure 4 displays the power of RF variable importance measures in selecting Gene 1 for Model 1 in the left panel and Genes 1 and 2 (averaged) for Model 2 in the right panel. The results shown here are based on 200 observations, while those based on 500 observations are represented in online supplementary figures 4 and 5. Overall, there are minor differences between gini, overall, and out1 with power in the range of 0.3–0.4, while out0 does markedly worse in all four scenarios with power <0.2. Regardless, all measures perform consistently if not slightly better as the value of mtry increases. To calibrate the models, we reduced the effect sizes for larger sample sizes; therefore, the power for all measures does not noticeably increase with the sample size (online suppl. fig. 4). Additionally, the distance between out0 and the others persists. The type I error for these comparisons is displayed at the bottom of table 1. For both sample sizes and both models, the error (ranging from 0.14 to 0.05) is consistent over mtry with no remarkable differences between the four measures of variable importance.

Fig. 4.

RF results for the tagging SNP Model 1 and 2 simulations. For 200 observations, power is measured on the y-axis and mtry on the x-axis. The p value is adjusted for the 60 SNPs and nT = 1,000. The different lines correspond to the four variable importance measures. For Model 1, only the results for Gene 1 are displayed. For Model 2, the average power over Genes 1 and 2 is displayed.

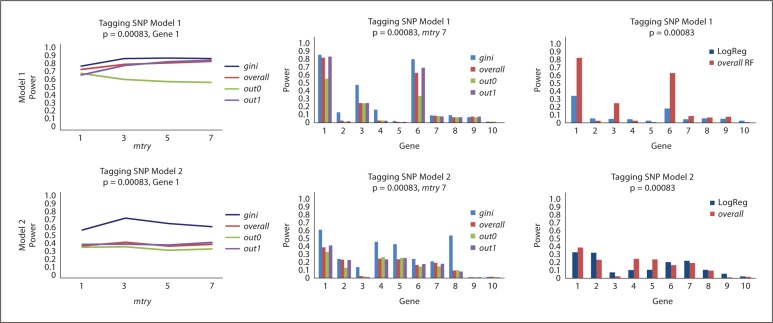
Figure 5 displays the power of RF and MCLR for Models 1 and 2 when dummy variables are used for the SNPs with a sample size of 500. The left panels of figure 5 show the power for detecting Gene 1 for each of the RF measures as mtry is increased. In Model 1, gini performs slightly better than overall and out1, while out0 performs the worst and slightly decreases as mtry increases. A more distinct difference between gini and the other measures is apparent in Model 2. Interestingly, for all four measures in Model 1 and for gini in Model 2, there is an obvious increase in power when dummy variables are employed as opposed to continuous valued SNPs (fig. 4) for selecting Gene 1. The middle panels of figure 5 compare the four measures for each of the 10 genes. For Model 1, the importance of genes 1 and 6 is detected by all measures; however, gene 3 is also frequently incorrectly selected. For Model 2, Gene 1 is the only one of the four correct genes (i.e. Genes 1, 2, 6, and 7) that is noticeably selected, while the type I error appears notable for most of the remaining genes. The right panels of figure 5 compare the overall measure for RF to that of MCLR over the 10 genes. For Model 1, RF correctly picks Genes 1 and 6 while frequently erroneously choosing Gene 3. MCLR has noticeably less power for the important genes and comparable type I error for the other genes, except that it does not erroneously choose Gene 3, resulting in lower error. In Model 2, MCLR is negligibly more apt to pick the important genes and similarly apt to choose the other genes. Importantly, both algorithms have power <0.2 for all genes except 1 and 2. As seen in online supplementary figure 5, the power for MDR for Models 1 and 2 is approximately 0 for all 10 of the genes. The left panel of online supplementary figure 5 displays the power of RF to detect the important genes when the variables are input as continuous. In contrast to the middle panels of figure 5 (which report the results when dummy variables are used), all measures with the exception of out0 have type I error close to 0 for the unrelated genes, while retaining marginal power to select the correct genes.

Fig. 5.

RF and MCLR results for tagging SNP simulations. Top row results are based on Model 1 and bottom row results on Model 2. Power is measured on the y-axis and dummy variables are used for the SNPs. RF results are presented only in the left and middle panels. In the left panels, mtry are on the x-axis and different lines represent different variable importance measures. In the middle panels, the power for RF (mtry = 7) for each of the importance measures is shown across all 10 genes. The right panels compare RF (overall importance measure, mtry = 7) to MCLR. For all results, there are 500 observations, nT = 1,000, and the p values are adjusted for 60 SNPs, i.e. 0.05/60 = 0.00083.

Computing. All simulations were run on the Yale University Biomedical High Performance Computing Center's Bulldogi, a cluster of 170 Dell PowerEdge 1955 nodes, each containing 2 dual core 3.0 Ghz Xeon 64 bit EM64T Intel cpus, for a total of 680 cores. Each node has 16 GB RAM. The three methods varied in computational requirements. To build a null distribution for n = 200 with 1,000 permutations for Model A, employing 10 nodes with 4 processors per node and using dummy variables, RF ran in <1 min, while MCLR ran in 7.5 min. For n = 500, RF ran in <1 min, while MCLR ran in about 16 min. In the same setting with continuous valued variables and n = 200, RF ran in <2 min, while MDR ran in 25 min. For n = 500, RF ran in about 3 min, while MDR ran in 63 min.

3.2. Data Analysis

In a recent study, collaborators at multiple institutions, including the National Cancer Institute, reported their findings on 1,321 newly diagnosed non-Hodgkin lymphoma (NHL) cases identified in four Surveillance, Epidemiology, and End Results (SEER) registries [18]. An additional 1,057 population controls were identified via random digit dialing and Medicare files. Of these, the researchers were able to collect biological samples on a total of 1,172 cases and 982 controls. The data is fully described in Chatterjee et al. [19].

The goal of the study was to evaluate associations between 57 SNPs in pro-inflammatory and other immunoregulatory genes and risk of overall NHL as well as the risk of five subtypes. For the purposes of the evaluation, univariate logistic regression models were used to estimate odds ratios (OR) and 95% confidence intervals. The findings indicated that SNPs in two pro-inflammatory cytokines, tumor necrosis factor-α (TNF) and lymphotoxin-α (LTA), as well as a SNP in the innate immune gene Fcγ receptor 2A (FCGR2A), increased overall NHL risk. Both TNF and LTA were also implicated as increasing risk for the subtype diffuse large B cell (DLBCL).

The goal of the current data analysis was to investigate a multivariate perspective via RF. Our hope was that by examining the SNPs in concert with each other additional associations with both outcomes (DLBCL and NHL) would be unearthed. As in the simulations, the first step of the analysis was to build a null distribution based on permuting the case/control status labels of the collected cohort, here 10,000 times. Subsequently, the permuted labels were paired individually with the original SNP values and RF was run (note that missing SNP values were imputed as described in the online suppl. Section 3). For each of the 10,000 samples, the four variable importance measures were recorded. Finally, RF was run on the original data (with non-permuted case/control labels). This final set of variable importance measures was compared to the null distribution and p values were assigned as in equation 1. The results including the p values and ORs for the original univariate logistic regression models as well as the p values based on two RF measures, overall and out1, for both outcomes (DLBCL and NHL) are shown in table 2. To estimate the false discovery rate, we employed the R, bioconductor package LBE which bases the q value estimation on the marginal distribution of the p values without an assumption for the alternative hypothesis [20,21]. Shaded p values in table 2 indicate corresponding LBE q values <0.2.

Table 2.

Data analysis combined results

	% genotypes missing n= 1,713	NHL				DLBCL
		univariate logistic regression		RFs		univariate logistic regression		RFs
		OR	P	overall P	outl P	OR	P	overall P	outl P
CCR2_01	0.04	1.0118	0.731			1.0257	0.5218
CCR5_01	0.04	0.9732	0.3819			1.0037	0.9177
CTLA4_01_2	0.07	1.0121	0.6383			1.0334	0.2742	0.0594	0.0786
CX3CR1_01	0.32	0.9836	0.5717	0.0021	0.0002	0.9809	0.5569	0.0149	0.0004
CXCL12_01	0.03	0.9565	0.0803	0.0235		0.9755	0.4012	0.2011
FCGR2A_01	0.03	1.0537	0.0677	0.1212		1.0259	0.4358		0.0628
ICAM1_01	0.03	1.3112	0.1819			1.2319	0.5174		0.2743
IFNG 07	0.05	0.9815	0.4482			0.9926	0.7972
IFNG_10	0.05	0.9845	0.5279			1.0002	0.9954
IFNGR1 05	0.30	0.9512	0.1385	0.0277	0.0003	0.9926	0.8405	0.0036	0.0001
IFNGR2_01	0.02	0.9595	0.135			0.9297	0.0242	0.0390	0.0826
IL10_01	0.02	1.0178	0.4731			1.0217	0.455	0.0439	0.0717
IL10_02	0.02	1.0168	0.499	0.2258		1.0206	0.4787	0.0397	0.0182
IL10_03	0.02	1.0202	0.458			1.0314	0.3261
IL10_17_2	0.02	1.028	0.2688			1.0408	0.172		0.2549
IL10RA_02	0.02	0.9718	0.2778			0.9937	0.8394
IL12A_01	0.02	0.9666	0.2176			0.9666	0.2892
IL12B_04	0.04	1.0334	0.1942	0.1566		1.0414	0.1708	0.0264	0.2020
IL13_01	0.05	1.0239	0.3584	0.0687	0.0762	1.0345	0.2638		0.1879
IL13_03	0.01	1.0414	0.11			1.0591	0.0533
IL15_02	0.05	0.9745	0.3048			0.9408	0.0377
IL15RA_02	0.05	0.9797	0.4615			0.9868	0.6869		0.1387
IL16_02	0.04	0.9792	0.3928			0.9718	0.3201
IL16_03	0.03	0.9776	0.4073	0.1971		0.9716	0.366	0.2223
IL1A_01	0.03	0.9986	0.9542			0.9693	0.2726
IL1A_02	0.01	0.9977	0.9251			0.9669	0.2338
IL1B_01	0.01	0.9909	0.7061			1.0123	0.667	0.2071
IL1B_02	0.02	1.0151	0.5423			0.9737	0.3568
IL1B 03	0.02	0.9817	0.4472			1.0081	0.7763
IL1RN_02	0.02	1.0198	0.4185			0.9998	0.9943
IL2_01	0.02	0.9947	0.8279			1.0042	0.882
IL4_01	0.03	0.9599	0.1307	0.1193	0.0312	0.9843	0.6142
IL4_02	0.01	1.0312	0.3913			1.0377	0.3813
IL4_03	0.02	0.9632	0.1698	0.2698	0.0325	0.9732	0.389		0.2712
IL4R_23	0.03	0.9973	0.9161	0.2151		1.019	0.5284
IL5_02	0.03	0.9679	0.18			1.0062	0.8293	0.1214	0.0137
IL5_10	0.04	0.5675	0.048	0.2255		0.7443	0.2629
IL6_01	0.01	0.9665	0.182	0.2177		0.9757	0.4132
IL6_04_2	0.03	0.9598	0.109			0.9663	0.2582
IL7R_01	0.30	1.0187	0.5206	0.1392	0.004	1.0408	0.2146	0.0310	0.0007
IL8_01	0.05	1.0496	0.0724	0.0216	0.0338	1.0579	0.0738	0.0620	0.2068
IL8_04	0.05	1.0528	0.0543	0.1273		1.0562	0.0791	0.0855
IL8_05	0.05	1.037	0.1611	0.211		1.0416	0.1761	0.1313
IL8RB_01	0.06	1.0482	0.0843	0.0838		1.0363	0.2584	0.0658	0.2104
IL8RB_02	0.30	1.0304	0.3804	0.0531	0.002	1.0127	0.7367	0.0158	0.0004
IL8RB 04	0.06	1.0002	0.9927	0.2892	0.0792	1.0023	0.9386	0.1049	0.0080
JAK3_01	0.30	1.0246	0.4792	0.0657	0.0123	1.0351	0.3699	0.0435	0.0087
LTA 01	0.01	1.0654	0.0086	0.0144	0.0742	1.0831	0.0046	0.0001	0.0000
LTA_04	0.12	0.9546	0.0764			0.9066	0.0015	0.0642	0.0323
SELE_01	0.33	1.0461	0.2137	0.0038	0.0002	0.9748	0.5537	0.0355	0.0005
STAT1_01_2	0.32	1.05	0.0963	0.0054	0.0009	1.0553	0.1037	0.0008	0.0000
TLR4_01	0.04	1.0035	0.9288		0.991	0.8422	0.1831	0.0325
TNF 02	0.01	1.0748	0.0064	0.1839	1.0974	0.0028	0.0041	0.0055
TNF 04	0.04	1.0059	0.8825		0.9906	0.84	0.2170	0.0516
TNF 07	0.03	0.9637	0.2382		0.9622	0.287	0.1976
VCAM1 02	0.05	1.0309	0.2576	0.0671	0.9987	0.9683
VCAM1_05	0.04	0.9737	0.599		0.9347	0.2614

The table presents a list of SNPs in alphabetical order and the corresponding results for NHL patients as well as DLBCL patients. For each patient group, the univariate logistic regression OR and (unadjusted) p values are displayed. The shaded boxes indicate corresponding LBE q values <0.2.

RF is affected by an unbalanced number of cases and controls. In the NHL analysis, there were 966 cases and 747 controls; thus, the proportions were close. However, in the DLBCL analysis, the number of cases was reduced to 316. Several approaches for addressing this issue have been suggested: non-uniform misclassification costs and either oversampling or undersampling to balance the data [22]. For the DLBCL data, we employed both oversampling and a variation of undersampling. For the former, the majority of SNPs were considered significant for all four variable importance measures suggesting that oversampling inflates the significance of the variable importance measures. For the latter, we randomly selected 316 of the 747 controls to pair with the 316 cases. The null distribution was built and final analysis performed with just those 632 observations. The results are those shown on the right-hand side of table 2.

For the NHL analysis, of the 57 SNPs only 2 are univariately significant at the q value cutoff of 0.2. In comparison, there are 7 significant SNPs determined by the overall measure and 10 by out1 in the RF analysis. There is good overlap between the selected SNPs by the two measures including a number of SNPs with significance that are not evident in the univariate analysis. For the DLBCL analysis, only 3 SNPs are deemed univariately significant, while 19 are significant by each of the two RF measures. Again the overlap between the significant SNPs selected by overall and out1 is substantial. The results shown for DLBCL in table 2 point to cytokine polymorphisms in the Th1/Th2 pathway genes including IFNGR2, IL5, IL7R, and TNF; and the same SNPs were identified recently for the NHL subtype marginal zone B-cell lymphoma [23] as well as for IL10 in DLBCL and follicular lymphoma [24]. Interestingly, Lan et al. [24] found IL7R, JAK3, and IFNGR1 to be significantly associated with one or more NHL subtypes, but all three lost significance after adjusting for multiple corrections. In comparison, we found all three to be significantly associated with NHL and DLBCL after adjustment, attesting to the increased power of RF over univariate models. Similar to the results in Purdue et al. [25], polymorphisms in IL10, IFNGR2, and FCGR2 are associated with the subtype DLBCL but not overall NHL. Of note, in our results LTA 04 (rs2239704) is only significant in DLBCL as is true in Purdue et al. [25]; however, we additionally found LTA 01 (rs909253) to be significant for both NHL and DLBCL, which they did not. When studying the JAK-STAT pathway, Butterbach et al. [26] found IFNGR1 to be associated with DLBCL as also seen in our results. We also found STAT1 to be significant for both NHL and DLBCL; however, they focus more on STAT3 in their analysis. Overall, there is substantial overlap between the findings previously reported in the NHL literature and our analysis.

4. Conclusion

Until the present, much of the focus in cancer genetics has been on generating lists of univariately significant SNPs. However, these approaches have not been effective for elucidating the synergistic qualities of the numerous SNPs in complex diseases. As SNPs do not act one at a time, but rather in concert with numerous others, a compelling need exists to examine analytically sound and computationally advanced methods that elucidate a more biologically meaningful understanding of the mechanisms of cancer initiation and progression.

Although modern GWAS involve potentially hundreds of thousands of tagging SNPs, in this report we examine the performance of several methods in settings that involve a relatively small number of candidate SNPs for two main reasons. First, not all of the methods we study are currently scalable for the analysis of a large number of SNPs, and thus direct comparisons of the methods are not possible on the GWAS scale. However, relative power of the methods for detecting true multi-locus interactions that involve a relatively small number of SNPs is likely to be similar irrespective of the total number of SNPs studied. Thus, the knowledge we gain from smaller-scale studies can be potentially useful for deciding on strategies for the analysis of larger-scale studies. Second, we observe that current GWAS have led to the discovery of a variety of susceptibility SNPs for many complex traits. Given that these findings are generally considered robust and well validated, there is now increasing interest in exploring interactions among such known loci for a better understanding of the underlying biologic mechanisms. The scale of our study is directly relevant for such analysis.

The goal of our study is to assess a SNP-specific p value which simultaneously accounts for the influence of other SNPs. RF provides us with a convenient tool for measuring a variable's importance via four different values: the class-specific measures (one for each outcome), the mean decrease in accuracy over all classes, and the mean decrease in the Gini index. In the current implementation, for each of the importance measures, continuous values for each variable are returned that can subsequently be ranked by the user. However, no guidelines are available to indicate which of these variables are significant. Without such, the user must rely on arbitrary cutoff values. As described in Section 3.1, we accomplish our goal of evaluating a SNP-specific p value by generating a null distribution.

Multiple simulations were performed in order to evaluate this approach in RF, MCLR, and MDR. RF had the highest power when the mutations were additive (Model A) or exact (Model E), when the causal SNPs were located within 2 genes (tagging SNPs Model 1) and when the causal SNPs were located within 4 genes (tagging SNPs Model 2). MCLR performed similarly to RF in Models E and 2. In the other two scenarios, MCLR did not have as much power. Interestingly, when using tagging SNPs, RF had better power to detect the 6 disease-related SNPs with dummy variables and lower type I error for the unrelated SNPs when using continuous covariates. With dummy variables, RF and MCLR had similar power in Model 2 for both the related and unrelated genes, while RF had much greater power to detect the related genes in Model 1. MDR had low power to detect disease-related SNPs/genes in all simulation models.

In comparison, García-Magariños et al. [4] found that RF and CART performed as well as logistic regression and MDR when there were SNPs with marginal effects and unknown interactions in the presence of a large number of noise SNPs. In pure interaction models, they found that RF performed as well as MDR especially with large sample sizes. However, their simulations are limited to the overall importance measure and only the highest ranked SNP.

Given the results of our simulations, overall and out1 are the most reliable variable importance measures in RF, either performing consistently or better than the other two measures. This is in contrast to Kim et al. [27] where Gini identified more important variables. In additional simulations (data not shown), we noted that Gini is strikingly affected by the number of levels of a covariate, which has been noted in several other studies [8,28,29]. As also observed in Diaz-Uriarte and Alvarez de Andres [30], different values of mtry led to almost identical results. The exception is in Model E of epistasis where the default value of mtry performed better, similar to the results seen in Kim et al. [27].

Although we note that the frequency with which a variable is included in multiple models is a naive measure of variable importance, it is the suggested measure for MDR and MCLR. Recently, two algorithms which form forests with logic regression have been suggested, logicFS [31] and LogicForest (LF) [32], each with a variable importance measure. In LF, the variable importance measure for variable X_j is an average of the out-of-bag misclassification rate for each tree in a (logic regression) forest based on randomly permuting the values of X_j. The difference between the variable importance of LF and of logicFS is that the latter replaces permutation with the addition/removal of ‘prime implicants’ (i.e. predictor interactions) in each tree. Additionally, the returned variable importance measure in logicFS is for prime implicants which can be single variables but more frequently are interactions of two or more variables. LF returns a variable importance measure for each individual variable as well as for the prime implicants, i.e. interactions. To explore whether the variable importance of LF improved on that returned by MCLR, we compared the two in simulations for Model A and found that the power was slightly lower for LF than that reported for MCLR; therefore, we did not include the results here.

A limitation of the suggested approach for assessing a SNP-specific p value is the computational burden. In this study, the computational intensity is limited as we focused on candidate gene studies. In studies including thousands of SNPs, the approach would currently be infeasible. However, as computational intensity and memory requirements have limited the use of RF at the genome-wide level, software packages such as Random Jungle and Willow have recently been introduced [33,34]. The suggested approach could be implemented with such packages.

Supplementary Material

Supplemental Materials