Computational Investigation of DNA Detection using Graphene Nanopores

Abstract

Nanopore-based single-molecule detection and analysis have been pursued intensively over the past decade. One of the most promising applications in this regard is DNA sequencing achieved through DNA translocation-induced blockades in ionic current. Recently, nanopores fabricated in graphene sheets were used to detect double-stranded DNA. Due to its sub-nanometer thickness, graphene nanopores show great potential to realize DNA sequencing at single-base resolution. Resolving at the atomic level electric field-driven DNA translocation through graphene nanopores is crucial to guide the design of graphene-based sequencing devices. Molecular dynamics simulations, in principle, can achieve such resolution and are employed here to investigate the effects of applied voltage, DNA conformation and sequence as well as pore charge on the translocation characteristics of DNA. We demonstrate that such simulations yield current characteristics consistent with recent measurements and suggest that under suitable bias conditions A-T and G-C base pairs can be discriminated using graphene nanopores.

Nanopores have emerged as promising next generation devices for single-molecule detection.¹ Biomolecules, driven through nanopores by an external voltage, exhibit concomitant ionic currents with detectable transient changes. Different molecules block the pore to different characteristic degrees, resulting in ionic current blockade of different amplitude and duration. In the case of DNA, four nucleotides, namely A, T, G and C, in principle, yield distinct ionic current blockades. There has been a lot of effort to build DNA sequencing devices based on the expectation that a sequence-dependent blockade current can be resolved.^1,2

Biological protein pores, e.g., α–hemolysin, were the first nanopores for which the possibility of building a sensor to sequence DNA was explored.³ Experiments on α–hemolysin demonstrated reduction in current by an order of magnitude when a DNA molecule is present in the pore.^3,4 Although having shown much promise, the high sensitivity of protein pores to temperature, pH and applied bias has been a major drawback for use in practical applications.²

Solid-state nanopores, fabricated in membrane materials like SiO₂,⁵ Si₃N₄,⁶ Al₂O₃⁷ and plastic,⁸ have emerged as an exciting alternative to protein pores as they are not only robust to the environment but also permit manipulation of physical and chemical properties of nanopores, in addition to bringing the advantage of being readily integrated into semiconductor devices and chips.² There has been extensive study on double–stranded DNA (dsDNA) translocation,^6,9–20 single–stranded DNA (ssDNA) translocation^10,21 and protein translocation,^22,23 through solid-state pores. A wealth of interesting results have been obtained with solid-state nanopores such as translocation time as a function of DNA length,⁹ salt-dependence on ion transport during DNA translocation,^18,19,24 unzipping of DNA during translocation^13,25 and discrimination of ssDNA and dsDNA based on pore diameter.^10,26 However, solid-state nanopores are typically tens of nanometer thick, making it difficult to detect individual base-specific modulation in ion currents as multiple base pairs interact with the nanopore channel simultaneously.²⁷

Recently, proof of concept to realize and use graphene nanopores for DNA detection has been demonstrated experimentally.^28–30 Graphene is a material with extraordinary electrical and mechanical properties.³¹ It is the thinnest known material with thickness equal to one atomic layer of carbon ~ 3 Å,³² which is comparable to the DNA base pair stacking distance of ~ 3.4 Å, making the graphene nanopore a promising device for DNA sequencing. The experiments have shown current blockades associated with translocation of dsDNA in folded and unfolded conformations.^28–30 In experiments, the DNA moved at velocities too high to permit resolution of individual base pair-specific current blockades. However, researchers have estimated theoretically that at slow translocation speeds a spatial resolution of 3.5 Å can be obtained with a 2.4 nm pore; this resolution equals the spacing between single base pairs in DNA.³⁰ Another opportunity for sequencing DNA using graphene is based on transverse conductance fluctuation in a graphene sheet due to a tunneling current through DNA.^33,34 Several groups have reported first principle-based studies to identify base pairs using tunneling-current/transverse conductance based approaches.^35–37

Large scale molecular dynamics (MD) simulations, which resolve atomic level detail, have been used as a tool to study bionano systems,^38,39 and have been quite successful in investigating electric field-driven DNA translocation through α-hemolysin^4,40 and Si₃N₄^{10–12,41,42} nanopores. Such simulations should also faithfully describe electric field-driven transport through graphene nanopores.

In the present study, all-atom MD simulations were carried out to investigate microscopic kinetics of DNA translocation through graphene nanopores. Simulations were indeed successful in characterizing the relationship between pore diameter and open pore resistance. Strong effects of external voltage and DNA conformation on the ionic current blockade were seen in MD simulations, consistent with experimental observations. We also simulated DNA translocation through two functionalized pores, namely a positive-charged pore and a negative-charged pore, revealing a pore charge influence on DNA passage time. Finally we investigated the possibility of distinguishing A-T and G-C base pairs under suitable bias voltage conditions.

Results and Discussion

In the present study, we performed the series of all-atom MD simulations listed in Table 1, covering altogether 370 ns, to provide an atomic level description of DNA translocation through graphene nanopores as shown in Figure 1. The simulations characterize the influence of several key factors on ionic current signals expected to resolve DNA sequence, namely, pore size, strength of an external electric field, DNA conformation, and pore charge. The simulations suggest that A-T and G-C base patterns can be resolved. In our study, first the relationship between the resistance of a graphene nanopore and its size was determined through monitoring I-V curves in open pore MD simulations. Second, the effects of applied voltage bias on the kinetics of DNA translocation through a nanopore were investigated. Third, we simulated the translocation of partially folded double-stranded DNA to determine the effect of DNA conformation on current signals. Fourth, the influence of pore charge on DNA translocation was studied. Finally, we computed the blockage current caused by poly(A-T)₂₀ and poly(G-C)₂₀ duplexes to explore the feasibility of base pair resolution in graphene nanopores.

Table 1.

List of performed simulations.

	Number of atoms	Temperature (K)	KCl conc. (M)	DNA (bp)	Diameter of pore (nm)	Pore charge (e)	Voltage (V)	Time (ns)
SimA1	126,277	295	1	–	2	0	3.0	7
SimA2	126,308	295	1	–	3	0	3.0	7
SimA3	126,355	295	1	–	4	0	3.0	7
SimA4	126,435	295	1	–	5	0	3.0	7
SimA5	126,540	295	1	–	6	0	3.0	7
SimA6	126,653	295	1	–	7	0	3.0	7
SimA7	126,308	295	2	–	3	0	3.0	7
SimA8	126,308	305	1	–	3	0	3.0	7
SimB1	188,743	295	1	45	2.4	0	4.3	3
SimB2	188,743	295	1	45	2.4	0	2.5	5
SimB3	188,743	295	1	45	2.4	0	0.8	35
SimB4	188,743	295	1	45	2.4	0	0.1	50
SimC	217,053	295	1	55	3	0	2.1	14.5
SimD1	210,670	295	1	45	2.4	+3.6	1.0	23
SimD2	210,670	295	1	45	2.4	−3.6	1.0	28
SimE1	210,772	295	1	poly(A-T)45	2.4	0	0.1	20
SimE2	210,772	295	1	poly(A-T)45	2.4	0	0.3	20
SimE3	210,772	295	1	poly(A-T)45	2.4	0	0.5	20
SimE4	210,772	295	1	poly(A-T)45	2.4	0	1.0	10
SimE5	210,772	295	1	poly(A-T)45	2.4	0	1.2	10
SimF1	210,772	295	1	poly(G-C)45	2.4	0	0.1	20
SimF2	210,772	295	1	poly(G-C)45	2.4	0	0.3	20
SimF3	210,772	295	1	poly(G-C)45	2.4	0	0.5	20
SimF4	210,772	295	1	poly(G-C)45	2.4	0	1.0	10
SimF5	210,772	295	1	poly(G-C)45	2.4	0	1.2	10

Figure 1.

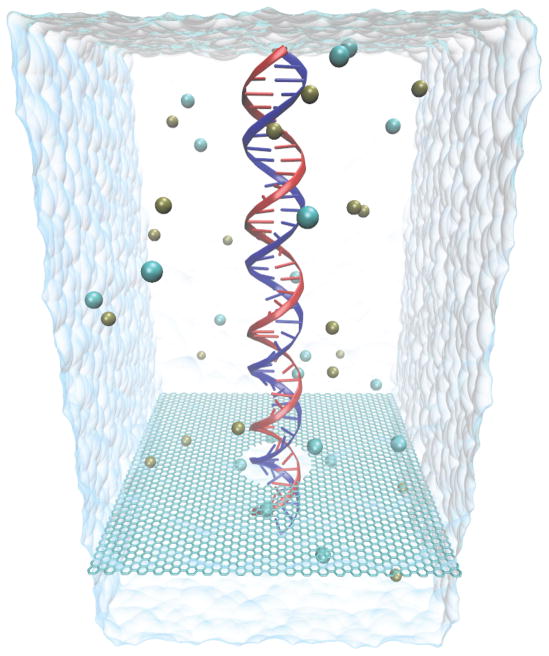
Atomic model of the graphene nanopore system simulated in this study. Shown is dsDNA in its initial upright position inside a graphene nanopore of 2.4 nm diameter; also shown are K⁺ and Cl⁻ ions, as well as the water surface at the boundaries of the simulated periodic cell (96 Å × 96 Å × 220 Å).

Open nanopore resistance

The ability of MD simulations to faithfully reproduce electric field-driven transport of ions through nanopores is crucial in describing DNA translocation-induced blockades in ionic current, presumably the signatures for DNA sequences, motivating the study of open pore characteristics of graphene membranes.

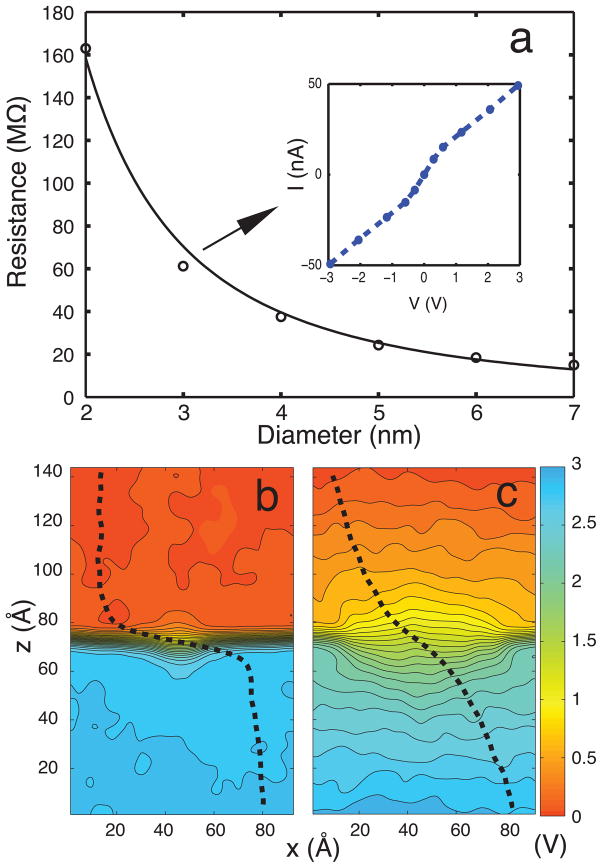
In order to assess the accuracy of MD simulations in describing ionic conductance of graphene nanopores, we compare the characteristics of nanopore resistance obtained from simulations with experiment. For this purpose, a series of all-atom MD simulations were carried out for the ionic current through open pores (for 1M KCl) with pore diameters in the range 2–7 nm (see simulations SimA1–SimA6 in Table 1). Anions and cations are driven in opposite directions by an external electric field, resulting in a net current. Figure 2 shows the open pore resistance as a function of pore diameter d. The resistance is determined as 〈I〉/V where 〈I〉 is the average ionic current through the pore during a 7 ns MD simulation. The dependence of resistance on the pore diameter follows closely the relationship R ~ 1/d², which agrees qualitatively with experiment.²⁸ The resistance values obtained through simulation are 3–4 times smaller than corresponding values in experiments. The discrepancy is attributed to: (i) higher voltage (3 V) used in simulations compared to experiments (0.1 V); (ii) the charge distribution and exact shapes of the graphene pores not being experimentally known; and (iii) inaccuracy of the force field assumed in the simulations that describes graphene-ion-water interactions poorly. The inset in Figure 2 shows a typical current– voltage (I-V) curve for a 3 nm-diameter pore at bias voltage of 3 V. The I-V curve is linear for low applied bias voltages. The motion of ions in the capture cross section of the pore is diffusion limited; hence, the linear I-V relationship breaks down at high fields.⁴¹

Figure 2.

Open pore characteristics. (a) Graphene nanopore resistance. Circles represent the open pore resistance of a nanopore with diameter varying from 2 to 7 nm (SimA1–SimA6). The solid line is a 1/d² fit to the circles (bias voltage is 3 V). The inset shows the I-V curve for a pore diameter of 3 nm. (b) Averaged potential map along the (x, z)-plane for a 2 nm diameter pore. (c) Same as in (b), but for a 7 nm diameter pore. The dashed line shows the potential change normal to the graphene membrane, illustrating the highly non-uniform potential profile.

To understand the size-dependence of pore resistance, the mean electrostatic potential in the system was calculated. Figure 2b, c show the averaged electrostatic potential maps in the (x, z)-plane for pore diameters of 2 and 7 nm, respectively. The potential maps for 3, 4, 5 and 6 nm diameter pores are provided in Supplementary Material (Figure S1). The potential maps illustrate that most of the potential drop arises across the membrane, not in the bulk. The potential drop becomes sharper near the membrane as the size of the pore decreases.

Simulations also revealed significant graphene membrane fluctuation (see movies, S1–S7, in Supplementary Material). The magnitude of the fluctuation, reflecting a “breathing” of the nanopore, can be as large as the nanopore thickness (see Table S1 in Supplementary Material). The breathing limits the spatial resolution of the ultra-thin graphene membrane to a value above its physical membrane thickness. Furthermore, the simulations show that increasing KCl concentration (SimA7) enlarges the fluctuation due to the increased number of voltage-driven ions colliding with the graphene membrane; an increase in temperature (SimA8) also leads to larger breathing fluctuation amplitudes (see Table S1).

Voltage-dependent kinetics of DNA transport through nanopore

We studied the electrophoresis of dsDNA (45 bp) through a 2.4 nm diameter graphene nanopore at bias voltages of 4.3, 2.5 and 0.8 V (for 1M KCl). The pores used in experiments had diameters in the range 5–22 nm.^28,29 In order to observe translocation events on computationally affordable simulation timescales, the minimum applied voltage bias, which had to be assumed in simulations, was 4–8 times larger than the voltage bias applied in experiments.^28,29 In the simulations, DNA was placed initially in a linear head-tail configuration at the pore mouth (see Figure 1). The capture of DNA by the nanopore requires DNA to reach the pore by diffusion from the bulk and thread itself into the pore by crossing an entropic barrier.^43–45 For small pores the main potential drop arises in the pore (see Figure 2b) and, therefore, DNA can be captured in this case only after it has diffused close to the pore mouth. Simulation of the capture process itself would require long simulation times. Since we are interested in the kinetics of the actual DNA translocation through the pore, not in the capture of DNA, we placed the DNA in all simulations at the pore mouth.

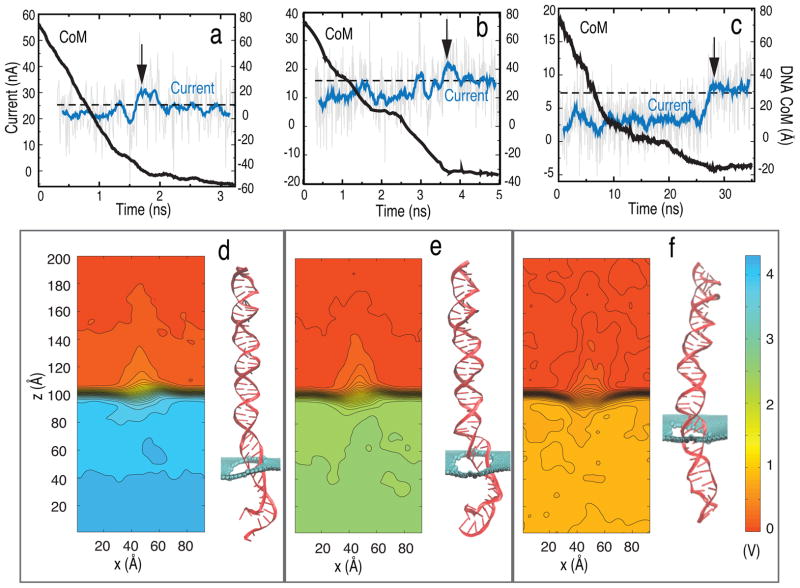
Figure 3a–c show, for different bias voltages (4.3, 2.5 and 0.8 V), the time evolution of ionic current and displacement of the DNA center of mass (CoM) when DNA translocates through the graphene nanopore. The potential maps along with typical DNA conformation are also shown in Figure 3d–f. A characteristic blockade of the ion current occurs when DNA resides in the nanopore; when it exits the pore, the current returns back to the open pore value. For 0.8 V, the reduction in pore current during blockade is 56%, for 2.5 V it is 34% and for 4.3 V it is 12% (more detail is provided in Table S2 in Supplementary Material). Apparently, DNA blocks the current more effectively at lower bias voltage. At high bias voltage (4.3 V), DNA is stretched to a larger extent compared to low bias voltage, 0.8 V, as shown in Figure 3d, allowing more ions to pass through the pore and resulting in less blockage of the current. The stretching of DNA at high bias voltages also explains the occasional overshoot of the blockade current above the open pore value. A spike in ion current is observed when the DNA leaves the pore and is due to rushing of clouds of K⁺ and Cl⁻ ions (which accumulate near the pore mouth due to blockade by the DNA) through the empty pore once the DNA exits;⁴¹ the overshoot is more prominent at higher bias voltages.

Figure 3.

Electrophoresis of dsDNA through graphene nanopores. Shown is the ionic current (blue line) and position of DNA center of mass (black solid line) for bias voltages of (a) 4.3 (SimB1), (b) 2.5 (SimB2) and (c) 0.8 V (SimB3). The arrow indicates the time instance when DNA exits the pore. The black dashed line shows the average open pore current. Also shown is the averaged potential map in the (x, z)-plane for voltage biases of (d) 4.3, (e) 2.5 and (f) 0.8 V. A snapshot of DNA is shown at the right of each potential map (pore diameter is 2.4 nm).

The translocation time for the DNA through the nanopore is 1.6, 3.7 and 27 ns for bias voltages of 4.3, 2.5 and 0.8 V, respectively. When a high bias voltage (4.3 V) is applied across the pore, DNA near the pore mouth adopts a stretched structure throughout the translocation period. The electric field is much stronger than the attractive hydrophobic force between DNA and graphene, which keeps the DNA in a vertical conformation as it moves through the pore, preventing the DNA to stick to the graphene membrane. Some of the DNA base pairs also unzip due to the high field. The DNA CoM moves at a constant velocity as indicated by the constant slope of the DNA CoM (during the translocation period) seen in Figure 3a. In the low bias voltage case (0.8 V) the DNA initially moves in the pore keeping its vertical conformation and remaining unstretched, but at around 10 ns the DNA starts to stick to the graphene membrane due to strong hydrophobic interaction and slows down its CoM movement, as shown in Figure 3c. The adhesion of translocated base pairs to the graphene membrane causes DNA in the pore to be stretched to a larger extent and partially unzip. At 2.5 V applied bias voltage the DNA slowed down briefly at 2.2 ns due to hydrophobic interaction between a base pair and the graphene membrane, but the hydrophobic interaction was not strong enough compared to the applied field and, hence, did not decrease the translocation speed of DNA as indicated by the slope of the displacement of the DNA CoM in Figure 3b. All the above simulations are provided in the form of movies (S1, S2 and S3) in the Supplementary Material. The translocation time depends inversely on the applied voltage in the absence of DNA interacting with the membrane.^14,46,47 However, the translocation rate of DNA through narrow pores is strongly affected by the interaction between DNA and nanopore surface;¹⁷ the DNA translocation can even stall due to the interaction with graphene. The two slopes in the CoM time dependence seen in Figure 3c derive their distinctness from the role that the hydrophobic interaction plays during DNA translocation.

Finally, DNA translocation at a low bias voltage of 0.1 V (i.e., the bias voltage used typically in experiment) was simulated (SimB4), which resulted in 3 base pairs translocating through the graphene nanopore during 50 ns. Based on the corresponding translocation time of 17 ns/bp, the translocation time for a 45 bp DNA would be 0.75 μs at 0.1 V. This estimated time (0.75 μs), however, does not entirely take into consideration hydrophobic interactions of DNA with graphene, as the DNA in the 0.1 V simulation is just entering the pore mouth and does not yet establish strong hydrophobic interactions with the graphene membrane. The hydrophobic interactions are likely to increase the translocation time further. Figure S2 in the Supplementary Material shows the DNA CoM as a function of time for various bias voltages. In DNA sequencing applications the DNA can be held in a stretched conformation to prevent translocation stalling and DNA sticking to the graphene membranes.

Partially folded dsDNA transport

DNA is a flexible polymer chain that adopts many different conformations in solution. When the length of DNA exceeds its persistent length, DNA may permeate through large pores (d > 2 nm) in a folded conformation, rather than in a linear head-to-tail fashion (unfolded). In electronic measurements of DNA translocation through nanopores, different current signatures have been observed,^28–30 which were attributed to different types of translocation events. Translocation of folded DNA, which occupies at least twice the volume of unfolded DNA, resulted in stronger current blockades compared to unfolded DNA. ^9,46,48

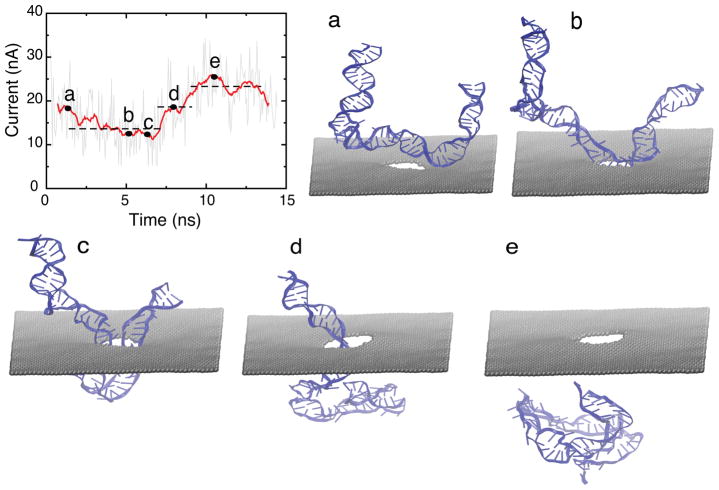
To provide an atomic level description of the translocation dynamics of partially folded DNA, we performed a MD simulation driving a 55-bp partially folded dsDNA through a 3 nm diameter nanopore (SimC). In the simulation, shown in Figure 4a–e, DNA was placed on top of the nanopore and close to the pore mouth. To ensure that DNA translocation happens on a time scale accessible for MD, a bias voltage of 2.1 V was applied. Under high electric field, the partially folded DNA permeated the nanopore in 15 ns. Figure 4 demonstrates that partially folded dsDNA translocation results in two different current blockades: (i) when DNA is captured by the electric field (Figure 4a), the folded part is stretched such that two dsDNA chains are in the pore simultaneously (Figure 4b); the folded part of DNA blocks the pore resulting in an average current of ~ 11 nA (Figure 4c). (ii) Once the folded part permeates through the pore, leaving only one dsDNA chain in the pore (Figure 4d), the average current increases to ~ 19 nA. When the entire dsDNA exits the pore, the current reaches an average value of ~ 26 nA (Figure 4e). The simulation reveals a characteristic double plateau current signature for translocation of partially folded dsDNA, which agrees well with experimental observation.²⁸ A movie (S4) showing the translocation of the partially folded DNA is provided in Supplementary Material. The movie also illustrates that the folded dsDNA adopts a stretched conformation in order to squeeze through the pore as the latter is geometrically narrower (d = 3 nm) than the folded dsDNA (which has a diameter d > 4 nm).

Figure 4.

Translocation of partially folded dsDNA (SimC). Shown is the time evolution of the ionic current. The three dotted lines correspond to plateaus in ionic current signature. Snapshots of DNA conformation during translocation is shown in (a) to (e): (a) initial conformation of dsDNA; (b) DNA captured by pore mouth; (c) both chains of folded DNA in the pore; (d) one chain leaves pore; (e) DNA exits the pore completely. The diameter of the pore is 3 nm and the bias voltage was 2.1 V.

Influence of pore charge on DNA translocation

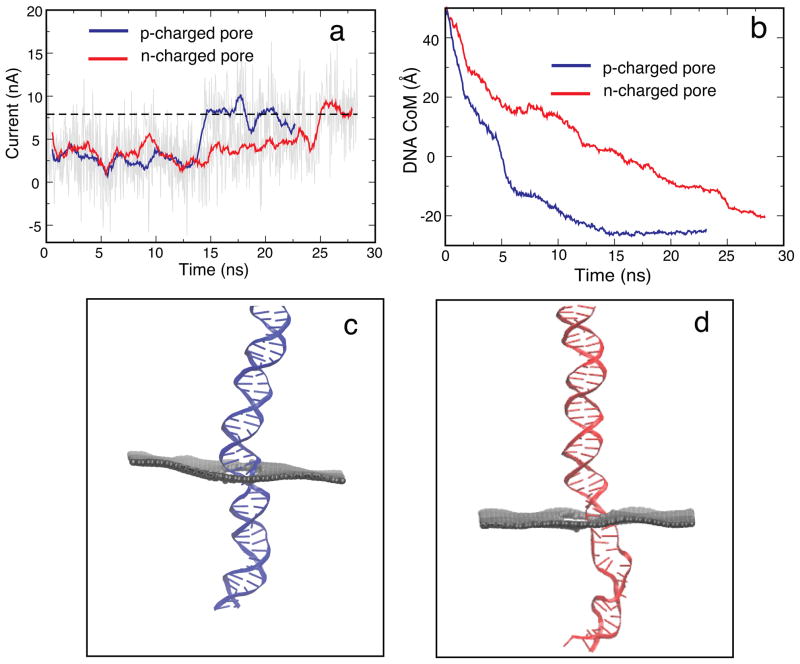
To determine the principle influence of pore charge on translocation kinetics of DNA, two pores with total charges ± 3.6 e were constructed, where each carbon atom on the pore mouth had a charge of ± 0.1 e. MD simulations on these two systems with bias voltage of 1 V were performed (SimD1 and SimD2). As shown in Figure 5a the translocation time for a negatively charged (n-charged) pore is 25 ns, while the translocation time for a positively charged (p-charged) pore is 15 ns. Figure 5b shows that DNA moves faster through a p-charged pore than through an n-charged pore. Since DNA is highly negatively charged itself, a repulsive interaction arises between a negatively charged pore and DNA which shrinks the diameter of the pore effectively. Figure 5c, d show that DNA adopts a conformation that is more stretched in the case of the n-charged pore than in the case of the p-charged pore. The stretched DNA blocks the pore to a smaller degree allowing more K⁺ ions to pass through the pore along with DNA, but opposite to it (see Figure S3 in the Supplementary Material), leading to a higher hydrodynamic drag and, thus, slowing down the DNA in the n-charged pore. Previous studies on solid-state nanopores also revealed a similar trend.⁴⁹ The above simulations suggest that pore charge can slow down DNA translocation. A movie (S5) showing the translocation of DNA through charged pores is provided in Supplementary Material.

Figure 5.

Effect of pore charges on translocation. (a) Ionic current for p-charged (SimD1) and n-charged (SimD2) pores. (b) Displacement of the DNA center of mass for p- and n-charged pores. (c) Typical configuration of DNA in the p-charged pore. (d) Typical configuration of DNA in the n-charged pore. DNA in the n-charged pore adopts a more stretched conformation than in the p-charged pore (The geometrical diameter of the pore is 2.4 nm, the bias voltage is 1 V and the total charge on the pore mouth is ± 3.6 e).

Detecting A-T and G-C base pairs with a graphene nanopore

Rapid DNA sequencing is a major goal of nanopore research. Previous studies pursued the goal to identify the four DNA bases (A, T, G, C) through analyzing current signals produced by DNA as it permeates through the nanopore.^{14,48,50–53} However, solid-state and biological nanopores have a pore thickness of > 5 nm,^2,19,46,54 which implies that multiple base pairs are inside the nanopore simultaneously. Hence, reducing the thickness of the nanopore is crucial for high-resolution DNA sequencing. Here, we demonstrate that A-T and G-C base pairs can be discriminated in dsDNA using an ultra-thin nanopore, namely a graphene nanopore with a physical membrane thickness of about 0.3 nm.³²

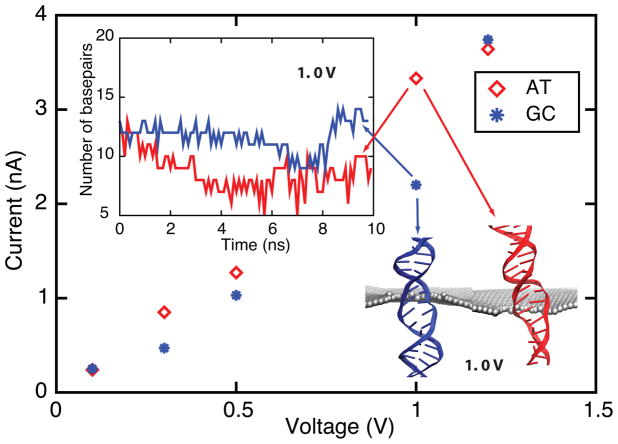
In MD simulations, poly(A-T)₂₀ and poly(G-C)₂₀ were inserted into a 2.4 nm pore and subjected to different bias voltages (0.1 V, 0.3 V, 0.5 V, 1.0 V and 1.2 V). To avoid DNA attaching to the graphene membrane, the two ends of DNA were subject to constraints, which allowed DNA to move freely only along the z-axis. Figure 6 demonstrates that at 0.1 V (lowest) and 1.2 V (highest) biases, the mean values of pore current of poly(A-T)₂₀ and poly(G-C)₂₀ are almost the same, while at intermediate bias values of 0.3 V, 0.5 V and 1.0 V the mean pore current of poly(A-T)₂₀ is larger than that of poly(G-C)₂₀. At 0.1 V, neither poly(A-T)₂₀ nor poly(G-C)₂₀ is stretched; hence, they block the nanopore to the same degree resulting in a pore current of ~ 0.2 nA. At 0.3 V and 0.5 V, stretched by electric field, the base pairs in poly(A-T)₂₀ and poly(G-C)₂₀ tilt in the pore mouth. Poly(A-T)₂₀ tilts slightly more than does poly(G-C)₂₀, resulting in a slightly larger ionic current. At 1.0 V, the base pairs in poly(A-T)₂₀ are more readily stretched and broken than those in poly(G-C)₂₀ (see snapshots in Figure 6 and movies, S6 and S7, in Supplementary Material), because an A-T base pair has one intermolecular hydrogen bond less than the G-C base pair. At 1.2 V the base pairs in poly(A-T)₂₀ and poly(G-C)₂₀ are mostly broken when they pass through the pore mouth (see Figure S4 in Supplementary Material) and, therefore, the values of the associated ionic currents are the same. Sequencing dsDNA using nanopores requires, at a minimum, discrimination between A-T and G-C base pair ionic current blockades. Our simulations suggest that it is possible to detect different base pair configurations in dsDNA using an appropriate voltage bias.

Figure 6.

Ionic current for poly(A-T)₂₀ and poly(G-C)₂₀ duplexes measured at 0.1 V, 0.3 V, 0.5 V, 1.0 V and 1.2 V transmembrane bias voltages in a 2.4 nm diameter nanopore (SimE1–SimF5). Translocation of A-T and G-C base pairs results in different ionic currents at 0.3 V, 0.5 V and 1.0 V. Snapshot shows that poly(A-T)₂₀ (red) is more stretched and disordered than poly(G-C)₂₀ (blue) at 1.0 V (see Supplementary Material movies S6 and S7). The inset shows the number of base pairs near the pore mouth (±2 nm): A-T base pairs are more readily broken than G-C base pairs at 1.0 V. Figure S4 shows the number of base pairs near the pore mouth for 0.1 V, 0.3 V, 0.5 V and 1.2 V.

Conclusions

Prior experiments have been successful already in detecting dsDNA molecules using graphene nanopores,^28–30 suggesting graphene to be a new promising material for cheap, rapid DNA sequencing with nanopore technology. To achieve single-base resolution, development of graphene-based DNA sequencing devices requires atomic scale pictures of the kinetics of DNA translocation and concomitant ion currents through the graphene nanopore. In this study, we have provided such detailed picture employing molecular dynamics simulations as a computational microscope. Simulations reveal how ionic current blockades strongly correlate with the local conformation of DNA inside the pore, linking the prior experimental observations to the underlying molecular mechanisms.

A key result of our study is that the size of the pore affects the distribution of the electrostatic potential in the system: for small pores (d ≤ 3 nm) most of the potential drop occurs near the membrane; the potential drop broadens non-linearly for larger pore diameter (d ≥ 4 nm), suggesting that DNA molecules can be more readily captured by a larger pore than by a smaller pore beyond the effect expected by pore area only.

Another key result is that pore charge can be used to control the kinetics of DNA translocation through a graphene pore. Previous studies reported that functionalized graphene nanopores furnish molecular sieves for ions.⁵⁵ Simulations on permeation of DNA through two modified pores, namely a p-charged pore and an n-charged pore, reveal that under identical bias voltage conditions DNA passes through a p-charged pore faster than through an n-charged pore. The difference can be attributed to the change of the effective pore size for DNA translocation. The simulation trajectories clearly demonstrate DNA needing to adopt a stretched conformation to undergo translocation through an n-charged pore.

A third key result is that the force experienced by nucleotides in the pore can be tailored by varying the applied electric bias voltage to discriminate poly(A-T)₂₀ and poly(G-C)₂₀. Our simulations are only a first step in studying the feasibility of actual DNA sequencing using graphene nanopores, raising the possibility of implementing nanopore DNA sequencing using graphene. However, there are many hurdles on the route towards achieving this experimentally.^27,54

The use of graphene nanopores for DNA sequencing, as suggested here, would require avoiding DNA adherence to the graphene sheet in order to keep DNA stretched in the pore; such avoidance can be realized, keeping the DNA stretched, by using, e.g., optical tweezers. Undulating stretched DNA inside a nanopore using an AC field might exhibit sequence-dependent hysteresis in graphene based nanopores as it does in silicon nanopores.⁵⁶ Future studies might focus also on sequence-dependent translocation characteristics of single stranded DNA which was not investigated here due to lack of observational data. In addition to being a sequencing tool, graphene nanopores may also be used for single-molecule force spectroscopy, e.g., to examine the binding force and energy of protein-DNA complexes at a single-molecule level.^2,57

We note that the π electrons in the graphene membrane are delocalized and, hence, can be readily polarized by the charged DNA and ions passing through the nanopore. Our present simulations do not account yet for such polarization, but they can be extended following the scheme used in the case of carbon nanotubes.^58,59 It is highly desirable to account for such polarization in future modeling, not only because it affects the force experienced by DNA inside the graphene membrane, but also since the polarization can be possibly used as a signal to further identify a passing DNA sequence. Electronic properties of graphene based nanopores can be tailored by employing bilayer graphene membranes, which have tunable bandgaps,^31,60–63 and graphene nanoribbons,⁶⁴ which can further increase the role of the membrane in electrically sensing and controlling the translocation process.

In summary, our MD simulations illustrate at an atomic level that magnitude and duration of the ionic blockade current in graphene nanopores with passing DNA can identify the local configuration of DNA, e.g., the extent of stretch, inside the pore as well as the composition of DNA. The geometry of DNA inside the pore depends on external voltage, the physical and chemical properties of the pore as well as on DNA sequence. Understanding the influence of each factor on the ionic blockade current signature stemming from translocation of DNA will provide guidance in the design of graphene-based DNA sequencing devices and single molecule sensors.

METHODS

System setup

The lattice points r⃗_mn for the graphene membrane used in the simulations, r⃗_mn = ma⃗₁ + na⃗₂, m, n ∈ ℤ, were constructed using 2-D lattice vectors ${\overrightarrow{a}}_1=\left(\frac{\sqrt{3}}{2}a,\frac{a}{2}\right)$ and ${\overrightarrow{a}}_2=\left(\frac{\sqrt{3}}{2}a,-\frac{a}{2}\right)$, where $a=\sqrt{3}\times a_{\text{C}-\text{C}}=2.46Å$ and a_C–C is the distance between two carbon atoms, namely, 1.42 Å. Each unit cell for graphene has two atoms, one at r⃗_mn and one at r⃗_mn + (a, 0). The pore is constructed by removing atoms whose coordinates satisfy the condition x²+y² ≤ d², where d is the diameter of the pore (Two pores with pore diameter equal to 2 and 6 nm are shown in Figure S5 in Supplementary Material). Periodic boundary conditions are applied at the boundary of the perforated graphene membrane simulated.

A double-stranded helix of DNA was built with the program X3DNA.⁶⁵ The topology of DNA along with the missing hydrogen atoms were generated using psfgen,⁶⁶ with the resulting topology files corresponding to the CHARMM27 force field.⁶⁷ The system comprising DNA and graphene was solvated in a water box. Ions (1 M KCl) were randomly placed in the water box in a stoichiometry that achieved charge neutrality in the final system. The simulation details are listed in Table 1. Simulations SimD1 – SimF5 were done with 1/3 of the DNA inserted into the pore allowing translocation events to be observed within affordable computer time., i.e., the simulations avoided the time consuming search of the DNA for pore entry. In simulations SimD1 and SimD2 each carbon atom on the pore mouth had a charge of ± 0.1 e. The value of 0.1 e is based on previous calculations on carbon nanotubes, the ends of which were terminated with H atoms; in this case the partial charges on C atoms are ≈ −0.1 e.⁵⁸

Molecular dynamics

All MD simulations were performed using the program NAMD2.7⁶⁶ employing periodic boundary conditions. CHARMM27 force field parameters were used for DNA,⁶⁷ TIP3P water molecules⁶⁸ and ions. The parameters for carbon atoms of graphene were those of type CA in the CHARMM27 force field,⁶⁷ namely the type of benzene carbons. The integration time step used was 1 fs with particle-mesh Ewald (PME) full electrostatics with grid density of 1/ų. Van der Waals energies were calculated using a 12 Å cutoff. A Langevin thermostat was assumed to maintain constant temperature at 295 K.⁶⁹

The system was first minimized for 4000 steps, then heated to 295 K in 4 ps. After heating, 500 ps-equilibration with the DNA constrained was conducted under NPT ensemble conditions, using the Nosé-Hoover Langevin piston pressure control at 1 bar.⁶⁹ To prevent drift of the graphene membrane, carbon atoms at the boundary were restrained using harmonic forces with spring constant of 1 kcal mol⁻¹ Å⁻². After the system acquired a constant volume in the NPT ensemble, 1.5 ns-equilibration was conducted in an NVT ensemble, constraining the end of DNA nearest to the pore. Finally, simulations were carried out as listed in Table 1 by applying a uniform electric field, directed normal to the graphene membrane, to all atomic partial charges in the system. The corresponding applied potential is V₀ = −EL_Z, where L_Z is the length of the simulation cell in the z-direction. The atoms rearrange themselves to produce an actual potential V (the sum of the potential from all simulated charges plus the applied voltage) with a profile that is non-uniform across the graphene membrane (see, for example, Figure 2).

Data analysis

In electronic measurements one can observe temporary drops in the measured conductance, arising from translocating DNA molecules partially blocking the pore.^28–30 Therefore, magnitude and duration of the ionic blockade current reflect the properties of the DNA inside the pore. To characterize the ionic current under different DNA translocation conditions, we monitored the time-dependent ionic current I(t) in MD simulations. The total ionic current I(t) was computed as⁴¹

$$I(t)=\frac{1}{\mathrm{\Delta }t{L}_{\text{z}}}\sum _{i=1}^N{q}_i[z_i(t+\mathrm{\Delta }t)-z_i(t)],$$ (1)

where the sum runs over all ions, Δt was chosen to be 50 ps and z_i and q_i are the z coordinate and charge of ion i, respectively. L_z represents the system dimension in the z-direction.

To illustrate the influence of external voltage on the kinetics of DNA electrophoresis, potential maps were computed. The potential V(r⃗) due to DNA and ions in the system was computed by averaging the instantaneous electrostatic potential (corresponding to single trajectory frames) over the entire MD trajectory on a 3-dimensional grid representing positions r⃗. The applied linear potential is then added at each grid point to give the final potential. The procedure is described in detail in.⁴⁰ The snapshots of the molecular structure from the MD simulations were depicted with VMD.⁷⁰