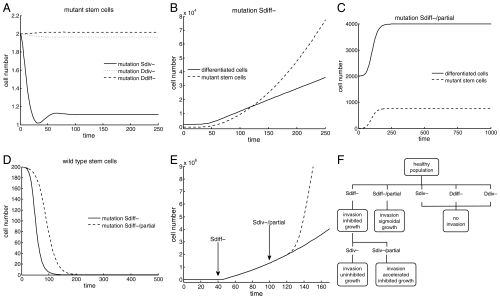
Fig. 2.

Evolutionary dynamics of feedback loss in the ordinary differential equations model. The simulations begin at equilibrium with two stem cells carrying the specified mutation. (A) For populations near equilibrium mutations Sdiv-, Ddiv-, and Ddiff- do not confer any competitive advantages over their wild-type counterparts. If the mutation arises in a small number of cells, the steady-state number of mutant stem cells will be negligible. (B) Mutation Sdiff- results in inhibited growth in the number of mutant stem cells and differentiated cells. (C) Mutation Sdiff-/partial produces a finite increase in both the number of mutant stem cells and differentiated cells. (D) Mutations Sdiff- and Sdiff-/partial result in the extinction of the wild-type stem-cell population. (E) In a healthy population at equilibrium, a stem cell acquires mutation Sdiff- at the time indicated by the arrow (solid line); the subsequent appearance of mutation Sdiv-/partial in a Sdiff- cell produces an acceleration in the growth of the tumor (dashed line). (F) Tumor progression toward uninhibited growth follows a unique sequence of feedback inactivations: First, mutation Sdiff- must occur, followed by mutation Sdiv-.