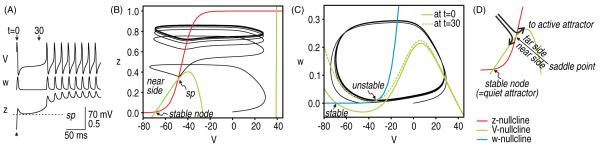
Figure 2.

Visualizing the interaction between multiple variables. We constructed a one compartment Morris–Lecar-type model to investigate the initiation and termination of afterdischarge. For initial tests shown here, g_NaP = 1.0 mS cm⁻² and g_Na = 20 mS cm⁻². (A) Time series show the co-evolution of V (which controls instantaneous activation of g_Na), w (which controls activation of g_K) and z (which controls activation of g_NaP). Both w and z are voltage dependent but do not change instantaneously with V. A single spike was evoked at time 0 by re-setting V to 0 mV and then letting the system evolve freely. To visualize how those variables interact, we can plot variables against one another (as in B and C) rather than against time (as in A). Furthermore, rather than trying to visualize interactions in 3D space, dynamical interactions can be analyzed in terms of the component 2D systems; in other words, we ask how V and z interact (on a relatively slow timescale) and how V and w interact (on a faster timescale during which z stays relatively constant). (B) The first interaction is visualized on the V–z phase-plane. The system normally rests at the stable fixed point in the bottom left corner. The V–z trajectory is seen to pass on the far side (relative to the stable fixed point) of the saddle point (sp) following the evoked spike. Having traversed the saddle point, the system moves toward its other attractor but enters a stable limit cycle and spikes repetitively rather than converging on a stable fixed point. (C) The onset of repetitive spiking can be understood from snapshots of the V–w plane at different time points indicated in A. At t = 0 ms, z = 0, which means g_NaP is not activated; under these conditions, the V- and w-nullclines intersect at the stable fixed point. At t = 30 ms, the evoked spike has caused an increase in z, which means g_NaP contributes an inward current. That current shifts the V-nullcline (green) from the solid position toward the dashed position. Upon sufficient shift, the intersection between the V- and w-nullclines is destabilized by a Hopf bifurcation and repetitive spiking ensues. Thus, generation of individual spikes depends on fast interaction between V and w, but the slow process responsible for a bifurcation in the V–w subsystem reflects changes in z. (D) The saddle point represents the border between two attractor states to which z can evolve following a perturbation. If z approaches the saddle point from the far side, the system will move toward its ‘active’ attractor, causing it to spike repetitively. If z approaches the saddle point from the near side, the system will return to its ‘quiet’ attractor or resting state. ‘Near’ and ‘far’ are defined relative to the quiet attractor.