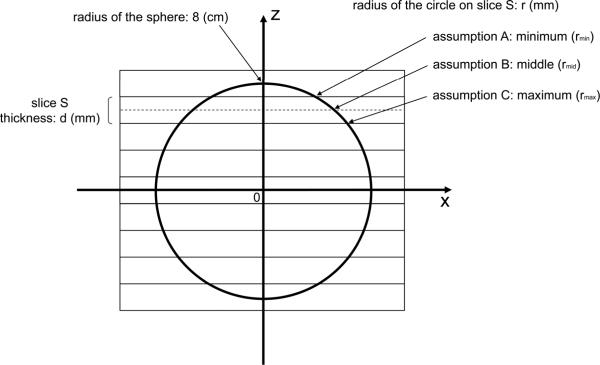
Fig. 1.

Drawing of the spherical model for numerical simulation shows a cross section of a sphere 8 cm in radius at y=0. The y-axis is perpendicular to the plane of the paper. The center of the sphere is located at the origin of the coordinate system. Rectangles show cross sections of CT slices, which are perpendicular to the z-axis, with both thickness and intervals of d mm. The center of the sphere is located at the middle of a slice and the center of the slice plane. For a given slice S, the volume of a part of the sphere within the slice S can be approximated by the volume of a cylinder with a radius of r mm and a height of d mm. The volume of the cylinder was calculated based on three assumptions for the radius: (A) minimum, (B) middle, and (C) maximum. The total volume of the sphere was approximated by the sum of the volumes of these cylinders.